ИСПОЛЬЗОВАНИЕ МОДЕЛИРУЮЩИХ КОМПЬЮТЕРНЫХ ПРОГРАММ В ПРОФЕССИОНАЛЬНО НАПРАВЛЕННОМ ОБУЧЕНИИ ГЕОМЕТРИИ
Атрощенко С.А.1, Первушкина Е.А.2
1Кандидат педагогических наук, доцент; 2Кандидат педагогических наук, доцент, Нижегородский государственный университет им. Н.И. Лобачевского, Арзамасский филиал
ИСПОЛЬЗОВАНИЕ МОДЕЛИРУЮЩИХ КОМПЬЮТЕРНЫХ ПРОГРАММ В ПРОФЕССИОНАЛЬНО НАПРАВЛЕННОМ ОБУЧЕНИИ ГЕОМЕТРИИ
Аннотация
В статье раскрываются методические аспекты организации профессионально ориентированного обучения геометрии с использованием динамических программных средств. Описана структура и содержание лабораторно-практических заданий, стимулирующих самостоятельную познавательную деятельность студентов, способствующие их профессиональной мобильности.
Ключевые слова: профессионально направленное обучение, познавательная деятельность студентов, интерактивная геометрия.
Atroshchenko S.A.1, Pervushkina E.A.2
1Candidate of Pedagogical Sciences, Associate Professor; 2Candidate of Pedagogical Sciences, Associate Professor, Lobachevsky State University of Nizhni Novgorod, Arzamas branch
USE OF THE SOFTWARE FOR PROFESSIONALLY DIRECTED TEACHING GEOMETRY
Abstract
The article deals with the methodical aspects of the organization of professionally directed geometry teaching using dynamic software. It describes the structure and contents of laboratory and practical assignments to encourage students’ cognitive activity, to contribute to their professional mobility.
Keywords: professionally directed teaching, students’ cognitive activity, interactive geometry.
В последние годы в качестве стратегической задачи развития высшей школы рассматривается формирование новой парадигмы образования, основанной на разработке и внедрении в педагогическую практику современных информационных средств, а также инновационных технологий обучения, направленных на развитие, прежде всего, личности специалиста–профессионала.
Ориентация современного образования на саморазвивающуюся личность предполагает учет индивидуальных особенностей, потребностей, обучающихся; предоставление им возможности выбора образовательных траекторий. В этой связи от вузовского преподавателя требуется умение не только осуществлять отбор содержания обучения по предмету, но и умение проектировать способы развертывания содержания в разных формах деятельности [1, 2]. Спроектированная модель обучения одновременно должна выполнять ряд функций: репрезентативную, эвристическую (стимулирующую познавательную активность студентов), диагностическую (позволяющую оценить сформированность усвоенных операций). Решение названной задачи при подготовке учителя математики видится, в частности, в дополнении традиционных практических занятий по геометрии и методики ее преподавания лабораторными работами, позволяющими сформировать у студентов умение использовать моделирующие компьютерные программы для построения изображений в планиметрии и стереометрии.
Так, в рамках курса по выбору «Образовательные электронные ресурсы по математике» разработаны и реализованы ряд лабораторно-практических работ по построению чертежей с помощью динамического программного средства GeoGebra [4]. Программа имитирует процесс построения циркулем и линейкой, давая возможность создавать «живые чертежи». Она написана Маркусом Хохенвартером на языке Java и имеет ряд преимуществ: во-первых, является свободно распространяемой и полностью поддерживает русский язык; во-вторых, установка GeoGebra достаточно проста и понятный графический интерфейс облегчает освоение основных действий в данной программе. Созданные в программе интерактивные работы можно сохранять в виде Java-апплетов динамических чертежей для их включения в веб-страницы.
Структура каждого занятия одинакова и содержит следующие компоненты: инструкцию, в которой описаны шаги основных построений; практическое задание на непосредственное построение конкретного изображения; задание для самостоятельной работы студентов – разработать инструкцию и выполнить изображение другой фигуры. Содержание занятий охватывает три укрупненные дидактические единицы: изображение многогранников, тел вращения и комбинаций пространственных фигур [3]. Например, результатом выполнения лабораторной работы по первой дидактической единице «Изображение правильной четырехугольной пирамиды» является модель указанного многогранника (рис.1–6), а также описание шагов построений и полученные изображения других многогранников. Построенные модели можно увеличивать и уменьшать, выполнять их геометрические преобразования, что позволяет проводить эксперименты по изучению свойств плоских и пространственных фигур. Кроме того, процесс моделирования можно анимировать и просмотреть как видеоролик.
Одним из путей реализации самостоятельной познавательной деятельности студентов на занятиях курса является их вовлечение в исследование.
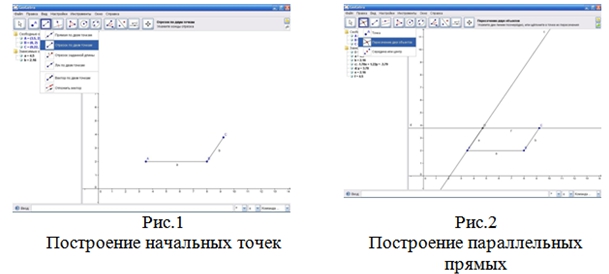
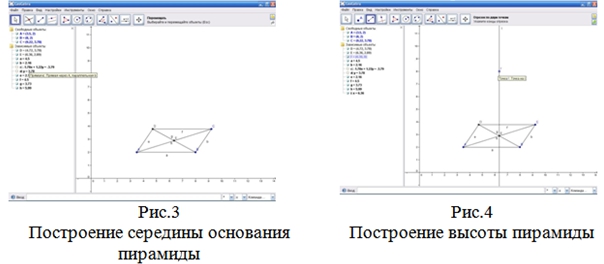
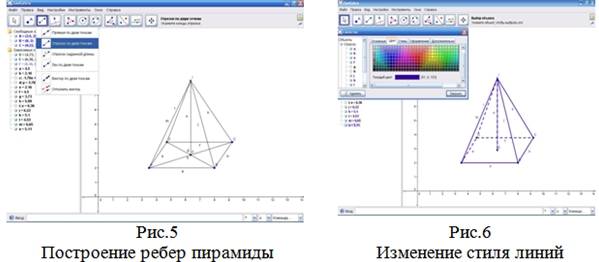
Мы выделяем шесть этапов исследовательской деятельности при выполнении заданий в процессе лабораторного практикума: иллюстрация исходного положение фигуры; формулировка задачи; изменение задачной ситуации; выдвижение гипотезы; исследование задачной ситуации; формулировка вывода [5, 6, 7]. Проиллюстрируем вышесказанное на примере.
- Очень важно, чтобы к задаче имелся чертеж, рисунок или другое средство, визуализирующее задачную ситуацию и вызывающее у студентов познавательный интерес. Поэтому на первый план следует поставить иллюстрацию исходного положения геометрической фигуры, чтобы исследователь мог ясно представить данную геометрическую ситуацию.
Рис. 7
- Формулировка задачи: Отметьте 3 точки, задающие остроугольный треугольник (см. рис.). Изобразите треугольник. Измерьте углы при основании треугольника и стороны, противолежащие им. Против какого угла лежит меньшая сторона?
- Следующим этапом является изменение задачной ситуации: задание движения элементов геометрической фигуры. При этом необходимо словесное описание движения каждого из элементов геометрической фигуры, изменение положения которого показывает его взаимосвязь с другими.
Изменение задачной ситуации (рис. 8): Поверните одну из сторон треугольника против часовой стрелки. В этом случае угол, образованный ею и другой стороной, начнет изменяться. При этом длина противолежащей стороны треугольника тоже станет изменяться. Проследите за этими изменениями, опишите их и охарактеризуйте взаимосвязь угла и противолежащей стороны треугольника.
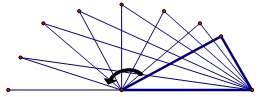
Рис. 8
- Важно приучить студентов к стилистически грамотным формулировкам гипотез, к стремлению уточнять значение каждого слова и смысл всего предложения. Гипотеза может быть записана как словесно, так и на математическом языке, что придаст ей большую точность. В данном примере гипотеза может быть сформулирована следующим образом: при увеличении угла при основании длина противолежащей стороны треугольника также увеличивается.
- При проведении исследования задачной ситуации сопоставляются фактические результаты с результатами, полученными на основе выдвижения гипотез.
В этом случае экспериментирование, проведение испытаний, возможных проб, попыток решения проблемы может быть связано с варьированием положения элементов фигуры, с рассмотрением предельных случаев, особых и промежуточных положений, допускающих обобщение.
Систематизацию и анализ полученных результатов полезно осуществлять на основе подходящих таблиц, диаграмм, схем, графиков и т.п., допускающих возможность визуального определения каких-либо свойств, связей, закономерностей (рис. 9).
| Испытания | 1 | 2 | 3 | Вывод |
| 1) величина угла при основании | ||||
| 2) величина угла при вершине, противолежащей основанию | ||||
| 3) длина противолежащей стороны |
Рис. 9
- Формулировка вывода предусматривает подробное описание каждого случая варьирования элементов фигуры с полученными результатами и раскрытие взаимосвязей элементов фигуры.
Для рассматриваемого примера: при увеличении угла при основании треугольника увеличивается длина противолежащей стороны. При этом величина угла при вершине, противолежащей основанию, уменьшается. (При уменьшении угла при основании треугольника уменьшается длина противолежащей стороны. При этом величина угла при вершине, противолежащей основанию, увеличивается.) Причём, когда вершина треугольника, противолежащая основанию, будет находиться на его продолжении, угол при основании станет равен развёрнутому, а угол при вершине, противолежащей основанию, – нулю.
Таким образом, изучение компьютерных программных средств и их реализация в ходе лабораторно-практических работ позволяет создать информационную обстановку, стимулирующую самостоятельную учебно-познавательную деятельность студентов, дающую возможность создать готовые сценарии применения моделирующих компьютерных программ по различным темам школьного курса геометрии.
Литература
- Атрощенко С.А., Нестерова Л.Ю. Интерференция математических компетенций в системе «школа – педвуз – школа» // Мир науки, культуры, образования. Международный научный журнал. 2012. № 3. С. 51-54.
- Атрощенко С.А. Формирование у учащихся базовых математических моделей задач эффективного управления // Международный научно-исследовательский журнал = Research Journal of International Studies. 2013. № 7-4 (14). С. 55-56.
- Атрощенко С.А. Теория и методика обучения студентов педвуза методам изображения геометрических фигур в контексте укрупнения дидактических единиц диссертация на соискание ученой степени кандидата педагогических наук / Арзамас, 1998.
- GeoGebra. Электронный ресурс – [Режим доступа] – http://www.geogebra.org/cms/ru/ (дата обращения: 12.07.2014 г.)
- Первушкина Е.А. Развитие геометрической креативности учащихся 5-6 классов средствами информационных технологий обучения Диссертация на соискание ученой степени кандидата педагогических наук / национальный исследовательский нижегородский государственный университет им. Н.И. Лобачевского. Арзамас, 2006.
- Первушкина Е.А. Модель развития геометрической креативности школьников при обучении математике в 5-6 классах с использованием информационных технологий // Школа будущего. 2011. № 6. С. 58-64.
- Пономарева Е.И., Первушкина Е.А. Развитие креативности школьников при обучении математике в 5-6 классах с использованием интерактивных геометрических сред // Перспективы науки. 2011. № 16. с. 27-34.
