INVESTIGATION OF THE HEAT-AND-MASS TRANSFER PROCESSES WITH COOLANT TEMPERATURE INCREASE AT DIFFUSION THROUGH TEMPERATURE INCREASING MATERIALS

Белов А.А.¹, Дараселия Н.В.², Швецов И.В.³

¹Аспирант; ²аспирант; ³доктор технических наук, профессор, Новгородский государственный университет им. Ярослава Мудрого

ИССЛЕДОВАНИЕ ТЕПЛОМАССООБМЕННЫХ ПРОЦЕССОВ ПРИ ПОВЫШЕНИИ ТЕМПЕРАТУРЫ ТЕПЛОНОСИТЕЛЕЙ ПРИ ДИФФУЗИИ ЧЕРЕЗ ТЕМПЕРАТУРОПОВЫШАЮЩИЕ МАТЕРИАЛЫ

Аннотация

Повышение температуры в жилых помещениях или на промышленных предприятиях необходимо для жизнеобеспечения. В статье рассмотрены новые технологии исследования тепломассообменнных процессов при повышении температуры теплоносителей при диффузии через температуроповышающие материалы без использования нагревательных элементов и устройств

Ключевые слова: тепломассообмен, температура, нагревательные элементы.

Belov A.A.¹, Daraselia N.V.², Shvetsov I.V.³

¹Graduate student, ²graduate student ³doktor of technical sciences, professor, Yaroslav-the-Wise Novgorod State University

INVESTIGATION OF THE HEAT-AND-MASS TRANSFER PROCESSES WITH COOLANT TEMPERATURE INCREASE AT DIFFUSION THROUGH TEMPERATURE INCREASING MATERIALS

Abstract

Rise in temperature in premises or at the industrial enterprises is necessary for life-support.The article deals with new technology research investigation of the heat-and-mass transfer processes with coolant temperature increase at diffusion through temperature increasing materials without the use of heating elements and devices

Keywords: heat-and-mass transfer, тemperature, heating elements.

Предлагаемая читателям работа направлена на решение фундаментальной проблемы тепломассообмена и диффузии газообразных теплоносителей через температуроповышающие материалы на основе газоаналитического и теплового отображения в газо- и гидродинамических системах. Основной задачей исследований является проведение сравнительного анализа различных моделей и сравнение результатов моделирования с экспериментальными и теоретическим результатами с целью проверки применимости математических моделей, их уточнения и развития.

Разработка моделей, отражающих особенности явлений и процессов в естественных и технологических физических системах в зависимости от внешних воздействий, является актуальной проблемой, которая исследуется в рамках различных направлений. Это актуально при развитии численных методов, построении алгоритмов, разработке программ и их реализацию для проведения компьютерных расчетов.

Определение значимых характеристик различных моделей может служить основой для их взаимного уточнения и развития, а также для разработки адекватных методов численного исследования, наиболее эффективных с точки зрения сокращения вычислительных ресурсов.

В ряде работ для снижения температуры воздуха описан вихревой эффект. Вихревое охлаждение впервые было предложено французским инженером Ж.Ж.Ранком в 1933 г. Французский инженер-металлург Жорж Жозеф Ранк (Ranque G.) первым провел целенаправленное экспериментальное исследование пылеотделителя - циклона и запатентовал первую вихревую трубу – устройство, использующее эффект «самопроизвольного» температурного разделения газовоздушного вихря на холодный осевой и горячий периферийный потоки.

Одним из малоизученных переходных процессов в физике является процесс нагрева газообразного или, тем более, жидкого вещества при прохождении через любой материал. Интерес к этой проблеме связан с экспериментальными исследованиями данных процессов и явлений, на не стандартном толковании термодиффузии. Проблемы, возникающие при исследовании этих задач, связаны с проблемой получения наиболее точного математического решения кинетических и термодинамических уравнений. Получение предварительной зависимости процессов больше усложняет задачу.

При свободной диффузии и наличии внешних сил основное уравнение диффузии в общем виде имеет вид

J = - D×ΔN;     (1)

J = - D×ΔN + v,    (2)

где J , ΔN и v - векторы потока, градиента концентрации и средней скорости дрейфа диффузионных частиц;

D - тензор второго ранга определяемый, как

	Dxx	Dyx	Dzx
D =	Dyx	Dyy	Dzy	(3)
	Dzx	Dzy	Dzz

Используя трехмерное уравнение непрерывности, скорость изменения концентрации во времени определяется как ΔJ = дN / дτ.     (4) Из выражений (1) и (2) получаем дN / дτ = ∇( D ×∇N);       (5) дN / дτ =  ∇( D ×∇N) - ∇( N, v) .      (6)

Уравнения (5) и (6) справедливы при исследовании диффузии для анизотропных тел. Для одномерной диффузии, а также для изотропных тел, в которых компоненты тензора коэффициента диффузии равны между собой, уравнения (5) и (6) принимают вид

дN / дτ = D · д²N / дx² + дD / дx · дN / дx ;      (7) дN / дτ = д / дx (D · дN / дx) - N · дv / дx - v · дN / дx    (8)

В случае независимости коэффициента диффузии от концентрации легирующих частиц применение уравнения непрерывности позволяет перейти ко второму закону Фика, устанавливающему связь между концентрацией диффундирующих атомов в различных точках тела и временем диффузии. Так для одномерного случая

дN / дτ = D · д²N / дx² .      (9)

При рассмотрении элементарного куба в случае трехмерного тела при отсутствии массопереноса в окружающее пространство общее уравнение диффузии имеет вид

дN / дτ = D · ( д²N / дx² + д²N / дy²  + д²N / дz²) = D ×∇²N,   (10)

где ∇²N - оператор Лапласа.

Из дифференциального уравнения следует, что концентрация или приращение концентрации имеется в точке равномерно распределенного объема. Если начальная концентрация N объема равномерна, то полное значение концентрации равно N + ΔN , где ΔN - приращение концентрации.

Решение уравнения (1) дает различные случаи распределения концентрации в объеме. При стабильных условиях коэффициент диффузии предполагается постоянным и изменяется в зависимости от температуры:

D = D₀exp(–A/RT),     (11) где D₀ – постоянная диффузии; А – энергия активации; R = 8,314 Дж/моль; Т = θ + 273,16 ⁰С – температура по абсолютной шкале Кельвина. Создание общей модели, проходящих процессов, является сложным и громоздким. Поэтому возникает необходимость объединить часть связанных между собой явлений. Решение уравнения (11) принимает различный вид в зависимости от начальных и граничных условий. Этот случай обычно реализуется при исследовании диффузии атомов из газовой фазы или из нанесенного на поверхность образца толстого слоя, когда на границе образца в течение всего диффузионного отжига поддерживается постоянная концентрация газа. В этом случае начальные и граничные условия следующие: 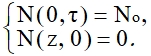        (12) Уравнение (1) второго закона Фика имеет следующее решение:  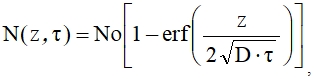            (13) где N_о – начальная концентрация атомов в металле; N (z, t) – концентрация диффундирующих атомов; z – ширина диффундирующего слоя; τ – время диффузии; D – коэффициент диффузии; еrf – функция ошибок Гаусса, которая определяется выражением  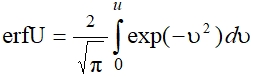       (14) Выражение (13) можно представить в виде дополнительной функции ошибок erfc, где  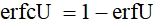       (15) Тогда  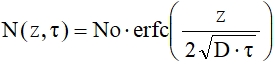          (16)

В предлагаемой модели предполагается, что законы диффузии действуют так же, как и при других процессах. В связи с этим, не нарушая основной принцип модели массопереноса и диффузии, полагаем, что миграция газовоздушных потоков в температуроповышающих материалах протекает согласно следующим положениям: законы диффузии газовоздушной среды (воздуха) выполняются по всему пути движения и соответствуют классической теории и на состояние газовоздушной среды (в данном случае увеличение температуры) оказывает трение ее молекул со стенками материала и скорость прохождения молекул в “лабиринтах” пористого материала.

Рассмотрим диффузию в условиях внешнего воздействия, заключающегося в выделении тепловой энергии, при повышении скорости потока газа и трении его молекул о стенки пористого температуроповышающего материла. Также происходит трение молекул газа между собой при повышении его концентрации внутри объема материала и увеличение длины пробега при увеличении скорости потока по всей длине материала и одновременном снижении площади сечения.

Решение уравнения диффузии принимает различный вид в зависимости от начальных и граничных условий. Этот случай обычно реализуется при исследовании диффузии атомов из газовой фазы или из нанесенного на поверхность образца толстого слоя, когда на границе образца в течение всего диффузионного отжига поддерживается постоянная концентрация примеси. В этом случае начальные и граничные условия отвечают выражению (13).

Время диффузии τ атомов определяется периодом действия внешних сил, когда поток диффундирующих элементарных частиц наибольший. Ширина диффундирующего слоя определяется размером температуроповышающего элемента.

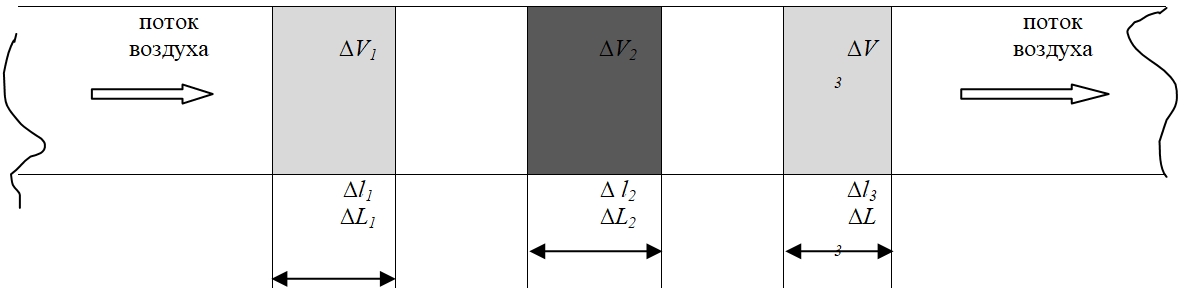
В соответствии с представленными выше данными остановимся на математическом выражении диффузии (11). Рассмотрим диффузию в воздухопроводе поэлементно. При этом должны выполняться следующие условия. При прохождении воздушного потока свободно без препятствий на элементарной длине ∆l₁ пройденный путь молекул воздуха будет равен ∆L₁. При прохождении воздушного потока через “лабиринт” пористого материала на элементарной длине ∆l₂ пройденный путь молекул воздуха будет равен ∆L₂. После температуроповышающего элемента продолжает проходить беспрепятственный массоперенос теплоносителя с повышенной температурой внутри воздуховода. Соответственно, после выхода из температуроповышающего материала элементарная длина будет ∆l₃ при дальнейшем массопереносе в трубе для элементарного пути ∆L₃, пройденного молекулами газа после выхода из температуроповышаюшего материала.

 

Рис. 1 – Схема массопереноса газовоздушного теплоносителя в воздухопроводе через температуроповышающий элемент: ∆l₁ – элементарная длина массопереноса в трубе; ∆l₂ - элементарная длина массопереноса в температуроповышающем материале; ∆l₃ - элементарная длина массопереноса в трубе после выхода из температуроповышающего материала; ∆L₁ – элементарный путь, пройденный молекулой газа в трубе; ∆L₁ - элементарный путь, пройденный молекулой газа в температуроповышаюшем материале; ∆L₃ - элементарный путь, пройденный молекулой газа после выхода из температуроповышаюшего материала

Во-первых, при прохождении воздушного потока через “лабиринт” пористого материала пройденный путь молекул воздуха ∆L₂ будет больше элементарной длины ∆l₂.

∆l₁ = ∆L₁,      (17) где  ∆l₂ ≠ ∆L₂, т.е. ∆l₂ ˂ ∆L₂.

Во-вторых, концентрация составляющих газов воздуха в газовоздушной смеси перед температуроповышающим элементом, в нем и после него будет одинаковой. То есть выполняется условие

N = N_O.   (18)

Характер массопереноса в элементарных объемах ∆V₁, ∆V₂ и ∆V₂ будет отличаться временем прохождения молекул газа и его трением в температуроповышающем материале о стенки материала. При этом значения коэффициента диффузии D₁, D₂ и D₃ в обоих случаях, при прочих равных условиях, будут также различны исходя из температуры теплоносителя.

Тогда, в соответствии с этим будет выполняться условие

D₁τ₁ = D₂τ₂         (19)

или τ_1×exp(-A/RT₁) = τ_2×exp(-A/RT₂)    (20)

Отсюда следует, что при увеличении температуры Т теплоносителя значения коэффициента диффузии D снижается и наоборот. То есть, для заданных условий выполняется условие

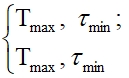          (21)

В основу физических моделей термодеформационных изменений заложено сочетание последовательного и параллельного взаимодействия факторов, имеющих механическую, механохимическую, химическую и сорбционную природу, определяющих многообразие и аномальность. Интерес к изучению различных преобразований связан с перспективой их применения в различных областях жизнедеятельности человека, а также с возможностью получения новой информации о структуре и свойствах материалов. Структура и свойства материалов изучаются экспериментально различными методами. Особое значение с точки зрения практических приложений имеет исследование динамики массопереноса через материал и повышение температуры.