ABOUT THE DEFORMATION OF THE OBJECTS WITH FLAT AND CURVILINEAR SURFACE UNDER THE SPRINGY CONTACT INTERACTION

Рамзаев А.П.¹, Сингатулин Р.А.²

¹Кандидат технических наук, доцент, Саратовский государственный технический университет им. Ю.А. Гагарина; ²доцент, Саратовский государственный университет им. Н.Г. Чернышевского

О ДЕФОРМАЦИЯХ ТЕЛ С ПЛОСКОЙ И КРИВОЛИНЕЙНОЙ ПОВЕРХНОСТЬЮ ПРИ УПРУГОМ КОНТАКТНОМ ВЗАИМОДЕЙСТВИИ

Аннотация

В работе исследуется упругое контактное взаимодействие системы с плоской криволинейной поверхностью. Постановка задачи заключалась в определении различия между расчетным некоторых авторов [1, 3] и экспериментальным значением деформации поверхностей в зоне контакта и величин упругих деформаций каждого тела. Сравнение результатов теоретических расчетов и экспериментальных данных позволяет оценить достоверность расчетных параметров упругих элементов и определить степень погрешности расчетного метода. В результате проведённых измерений был сделан вывод, что при определении деформации упругих тел необходимо учитывать сближение и упругие деформации с учётом их форм.

Ключевые слова: деформация, упругий контакт, плоская и криволинейная поверхность.

Ramzaev А.P.¹, Singatulin R.A.²

¹Candidate of Science, Associate Professor of the Chair of Instrument of the Construction, Saratov State Technical University named after U.A. Gagarina; ²Candidate of Science, Associate Professor of the Chair of Information Systems and Technology in Education, Saratov State University named after N.G. Chernyshevsky.

ABOUT THE DEFORMATION OF THE OBJECTS WITH FLAT AND CURVILINEAR SURFACE UNDER THE SPRINGY CONTACT INTERACTION

Abstract

The springy contact interaction of the system with flat and curvilinear surface is researched in the work. The statement of the problem was concluded in the determination of the difference between account and experimental meaning of the surfaces deformation [1, 3] in area of the contact and values springy deformation of each object. The comparison of result of theoretical calculation and experimental data allows valuing the validity accounting parameter of springy elements and defining the degree of the inaccuracy of the accounting method. As a result of measurements there was made a conclusion that in the determination of the deformation of the springy object it is necessary to take into account the rapprochement and springy deformation with the account of their forms.

Keywords: deformation, springy contact, flat and curvilinear surface.

1. Постановка задачи

При определении деформации упругих тел с плоской криволинейной поверхностью, при контактном взаимодействии, необходимо учитывать сближение и упругие деформации с учётом их форм. Контактное взаимодействие тел произвольной формы и кривизны при упругопластичном и упругом контакте рассмотрено в работе [1, 4]. При этом в этой и других работах приняты следующие допущения:

- со снятием нагрузки контур отпечатка не изменяется;

- профиль вмятин под нагрузкой и после разгрузки очерчены плоскими фигурами;

- поверхность тел вне контакта не деформируется, а контур тел остается плоским.

Последнее допущение справедливо, когда отсутствует выпучивание свободной поверхности деформируемого материала вблизи контура фактической площади контакта. Вопрос о боковом выпучивании и проседании тел рассмотрен Д. Тейбором [2]. Упругие контактные деформации тел обычно определяют по формулам Герца, когда тела считают идеальной формы. Шероховатость уменьшает жесткость слоя, снижает фактическое давление и учитывается в других работах (А.А. Ланков, В.Р.Д. Миндлин и др.). В работе В.Ф. Яковлева [3] приведены следующие условия, нарушающие предпосылки теории Герца-Беляева:

а) радиусы тел соизмеримые с их размерами;

б) геометрические формы и размеры контактирующих тел различны.

Расчетные напряжения, полученные по теории Герца-Беляева, одинаковы по всей контактной зоне (по поверхности и в глубине) в обоих контактирующих телах, условно принимаемых упругими полупространствами.

Для определения величины кривизны вмятины R1 приняты следующие допущения [8]:

1) со снятием нагрузки сферический контур отпечатка не изменяется;

2) профиль вмятины под нагрузкой и после разгрузки в плоскостях её главных кривизн очерчены окружностью радиусом R1;

3) поверхность контртела вне контакта не деформируется.

Перемещение точек плоской поверхности полупространства от действия сосредоточенной силы (Р) определяется выражением [6, с. 399]:

,

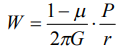где 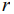- расстояние от точки приложения силы до точки, в которой имеет место перемещение  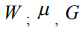- коэффициент Пуассона, модуль сдвига.

При давлении, пропорциональном ординате сферической поверхности и эллипсоида, перемещения точек плоской поверхности в зоне 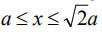, определяется выражением [6]:

,

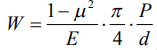где Е – модуль упругости, Па; Р – нагрузка, Н; d – диаметр, м; а – радиус площади контакта.

Для решения контактных задач между конструкцией и основанием используются коэффициент податливости основания или коэффициент постели по модели А.А. Саргсяна [7] для упругого полупространства. Этот коэффициент определяется в виде:

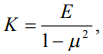
где К – коэффициент размерности н/м²; к = к₁b; к₁ - коэффициент податливости основания или пастели размерность Па/м;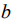- ширина подошвы упругой балки; а - деформация плоскости:

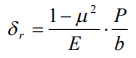
При упругом контактном взаимодействии шара 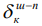, цилиндра  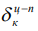с плоскостью применяют формулы [9]:

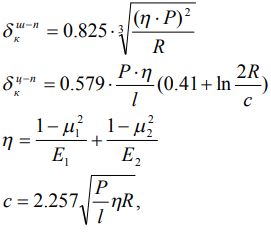
где δ - смещение расстояния между центром тел с криволинейной поверхностью и плоскостью; 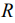- радиус шара, цилиндра; 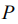- нагрузка; 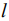- длина цилиндра;  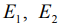- модуль нормальной упругости тел;  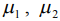- коэффициенты Пуассона тел.

Так как податливость контактного слоя для сфер и цилиндра с плоскостью (рис. 1) и упругого полупространства складываются, то деформация тела с криволинейной поверхностью равна:

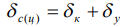
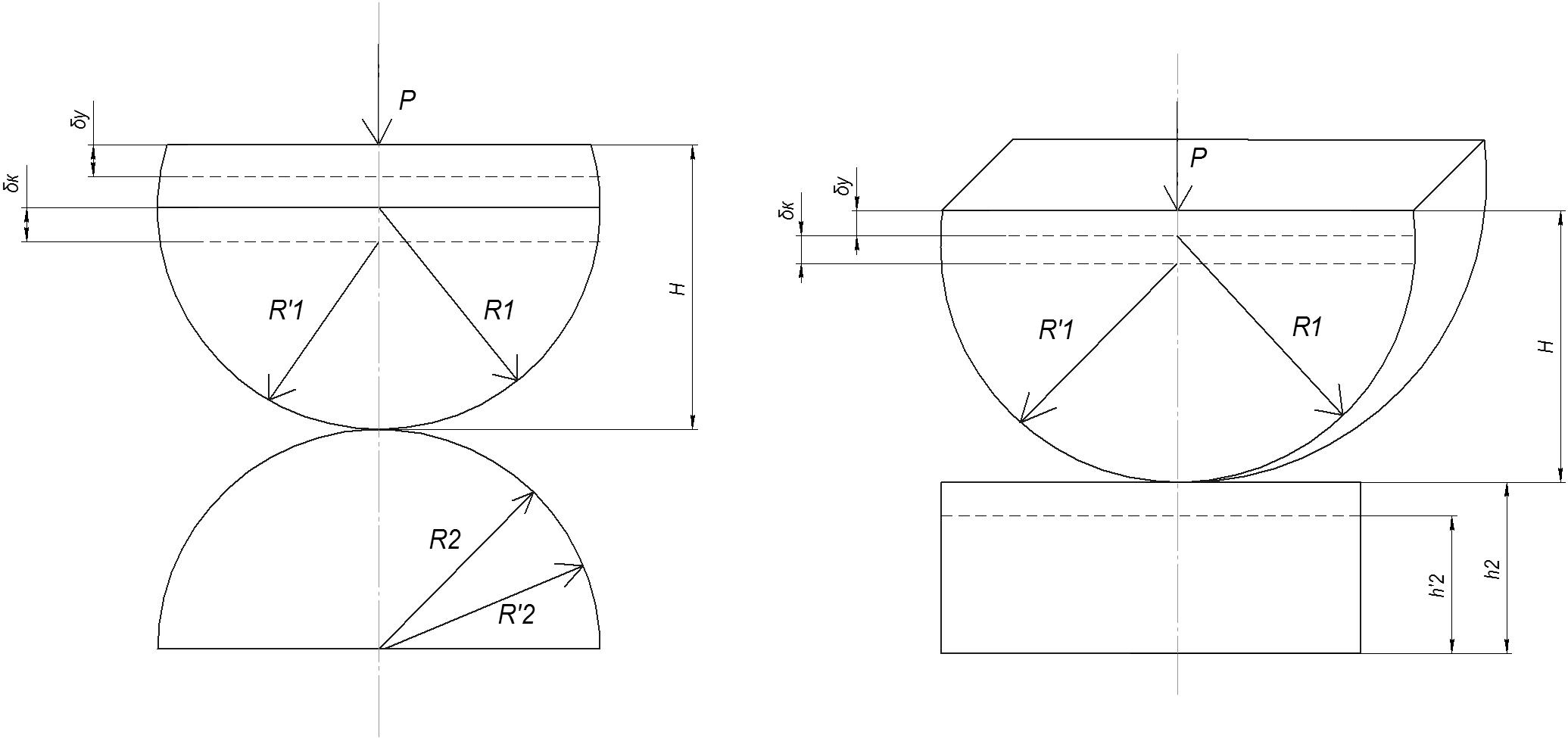
Рис. 1. Схема контактного слоя для сфер (а), цилиндров (а) и цилиндра с плоскостью (б)

Ставится задача – определение различия между расчетным и экспериментальным значением деформации поверхностей в зоне контакта и величин упругих деформаций каждого тела. Сравнение результатов теоретических расчетов и экспериментальных данных позволит оценить достоверность расчетных параметров упругих элементов и определить степень погрешности расчетного метода.

2. Решение задачи

Методика решения задачи заключается в следующем:

1) экспериментально определить значение модуля упругости для опытных образцов резины, силикона, органического стекла в виде прямоугольных стержней при сжатии;

2) изготовить образцы в виде сегментов сферы, цилиндра и плоских тел из стали, стекла, резины, силикона и органического стекла;

3) измерить зависимость деформации по направлению силы от нагрузки при взаимодействии тел с криволинейной поверхностью с плоскими телами.

Экспериментальные исследования заключаются в снятии упругих характеристик конкретных тел, т. е. в определении зависимости F=F(Р). Практически определяется величина деформации F упругого элемента при воздействии ряда нагрузок с определенным интервалом нагружения. Экспериментальной установкой является эластикометр. Он представляет собой устройство типа весов с компенсатором, кинематическая схема которого приведена на рис. 2.

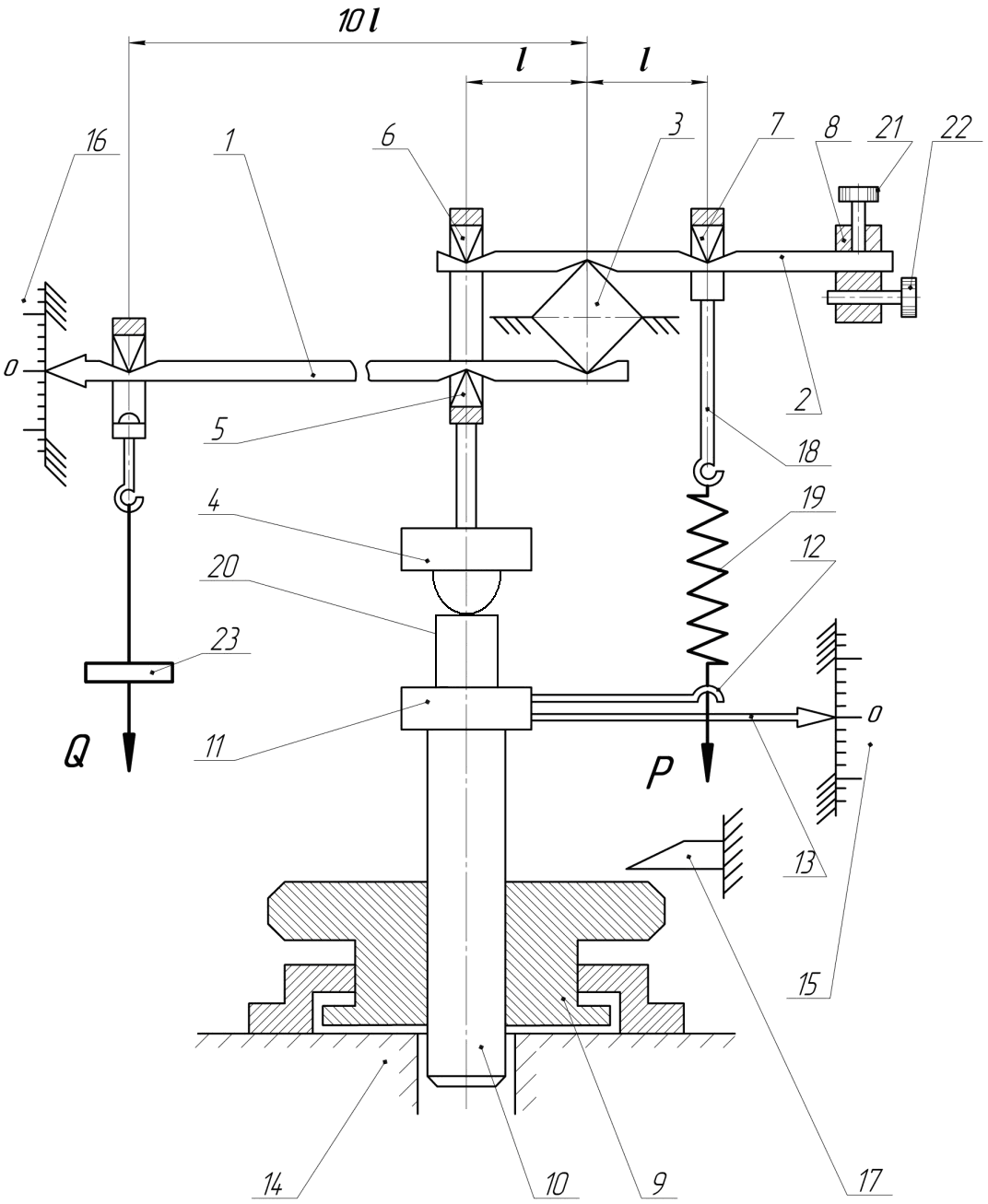
Рис. 2. Схема эластикометра

Усилие груза Q передается через рычаг 1, опирающийся на неподвижную призму 3, ножевые опоры 5, 6, рычаг 2, опирающийся на противоположную грань неподвижной призмы 3, ножевую опору 7 и через тягу 18 на исследуемую пружину 19. Далее через штифт 12, винт 10 и гайку 9 на станину 14. Для создания равновесия между грузом Q и усилием пружины 19, рычаг 1 приводится к «0» по шкале 16 за счет осевого перемещения винта 10, а следовательно и натяжения пружины 19. Винт 10 перемещается при повороте гайки 9. Величина перемещения винта представляет собой деформацию F пружины 19 при заданной нагрузке Q. Деформация фиксируется грубо указателем 13 на миллиметровой линейке 15 и точно указателем 17 по лимбу на гайке 9, цена деления которого 0,1 мм и дополнительному микронному индикатору 1 мкм. Соотношение плеч рычагов прибора 1:10, при этом одна единица Q соответствует 10Р.

Зависимость деформации вакуумной резиновой пластины с толщиной b=3,6 мм от усилия, носит нелинейный характер и определяет величину модуля упругости 0,5 и 4,16 кг/см², при s=2,404 см², а стержня из органического стекла (100х10х20) - 6000 кг/см².

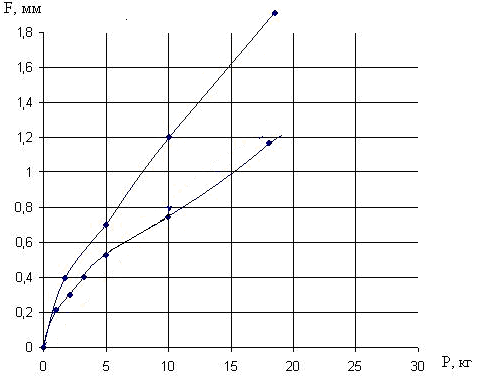
Рис. 3. Зависимость деформации цилиндрического образца из резины (верхняя кривая) и стекла (нижняя кривая)

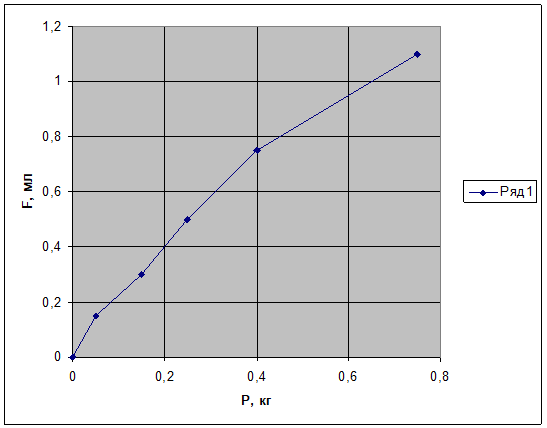
Рис. 4. Зависимость деформации сферического образца из силикона со стальным плоским образцом

Выводы

В результате экспериментальных измерений определены модули упругости образцов: силикон 9-15 кг/см, резина 60 кг/см, органическое стекло 6000 кг/см. Сближение полуцилиндра R=27,5 мм с высотой H=42 мм из резины с плоским образцом 1 из стекла 2 при нагрузке 15 кг равно 0,16 мм, а полуцилиндра из стекла с плоским образцом из резины равно 0,10 мм, которые совпадают с теоретическим значением по приведённым формулам при контакте резина - стекло и стекло - резина.

Измерения зависимости деформации от нагрузки при взаимодействии тел с криволинейной поверхностью с плоскими телами, позволяют проводить расчёты значение модуля упругости не только для образцов резины, силикона, органического стекла, но для керамики, гипса, дерева и других материалов.