NUMERICAL MODELING OF TEMPERATURE PARAMETERS OF SHOCK WAVE FLOW IN GAS SUSPENSION IN A CHANNEL WITH VARIOUS BOUNDARY CONDITIONS
NUMERICAL MODELING OF TEMPERATURE PARAMETERS OF SHOCK WAVE FLOW IN GAS SUSPENSION IN A CHANNEL WITH VARIOUS BOUNDARY CONDITIONS
Abstract
The article presents a numerical model of shock wave propagation in a channel from a homogeneous gas to a gas suspension – a suspension of dispersed particles in a gas. This topic is relevant due to various applications in technology. The carrier medium is modeled based on the Navier-Stokes equations. The mathematical model implements a continuum technique for modeling the dynamics of inhomogeneous media — for each component of the mixture, a complete hydrodynamic system of equations of motion was solved, momentum exchange and heat exchange between the components of the mixture were taken into account. The system of equations for the dynamics of the carrier medium and the dispersed phase includes density continuity equations, equations for conservation of spatial components of the carrier and dispersed phase momentum, and energy conservation equations. The equations of the mathematical model were solved by an explicit finite-difference method. A nonlinear grid function correction scheme was used to suppress numerical oscillations.
1. Введение
Так как математические модели процессов механики жидкости и газа являются нелинейными, для решения уравнений применяются численные методы. Среди гидродинамических процессов отдельно выделяют гидродинамические процессы с движением дисперсных сред. В отличие от гидро-газодинамики однородных сред , в неоднородной гидродинамике , , потоки сопровождаются взаимодействием компонент смеси , . В публикации разрабатываются трехмерные численные модели течений изотермальной вязкой ньютоновской многофазной. В работе с помощью методов гидродинамики неоднородных сред исследованы процессы взаимодействия ударных волн с газодисперсной взвесью. В статье также исследуется взаимодействие газа и дисперсных частиц. Рассматривались различные распределения концентрации дисперсных. В работе с помощью континуальной методики динамики неоднородных сред исследуются процессы взаимодействия газа и слоя дисперсных частиц. В исследовании рассматривались различные дисперсности частиц газовзвеси при взаимодействии газа и дисперсной завесы. В работе получены математические модели распространения ударных волн в газовзвеси в плане исследования технологических процессов горной промышленности. В статье численно моделируется ударно-волновые течения дисперсных сред.
Анализ работ, посвященных динамике неоднородных сред, демонстрирует, что в связи с проблемами горных и аэрокосмических технологий представляет интерес математическое моделирование ударноволновых течений газовзвесей.
2. Методы исследования
Для моделирования динамики газовзвесей на данный момент существует несколько подходов . Преимуществом математических моделей, разработанных в рамках континуальной концепции течений неоднородных сред является то, что такие математические модели могут более точно описывать динамику смесей с близкими массовыми долями компонент смеси, также такие модели позволяют моделировать течения с неоднородным распределением дисперсной фазы. В данной работе рассматривается течение, в котором происходит взаимодействие ударной волны, движущейся из однородного газа, с газовзвесью, дисперсная фаза которой имеет массовую долю близкую по значению с массовой долей несущей среды.
В данной работе моделируются процессы работы ударной трубы, заполненной однородным газом и газовзвесью, рассматриваются температурные поля несущей среды и дисперсной фазы для различных граничных условий скорости компонент смеси при моделировании течения газовзвеси в рамках континуальной модели динамики неоднородных сред. Математическая модель разработана на основе континуального подхода . Моделирование течения газа осуществлялось с двухмерным нестационарным уравнением Навье-Стокса для сжимаемой теплопроводной среды с учетом взаимодействия с дисперсной фазой, математическая модель описана в работе . Решение системы уравнений осуществлялось с помощью метода конечных разностей , .
Для улучшения численного решения применялась методика , .
Задавались два типа граничных условий. Для всех параметров несущей среды и дисперсной фазы задавались однородные граничные условия Неймана, для составляющих скорости газа и дисперсной фазы на границах расчетной области задавались либо однородные граничные условия Неймана, либо однородные граничные условия Дирихле. Такой выбор граничных условий связан с тем, что влияние граничных условий скорости на динамику потока может иметь существенное значение .
Для того чтобы определить работоспособность компьютерной программы, реализующей численную модель, было проведено сопоставление численных расчетов с физическим экспериментом . На рисунке 1 представлены сопоставления численных и экспериментальных результатов ударно-волновой динамики запыленных сред, изображены зависимости числа Маха фронта ударной волны от начального перепада давления. Сопоставляются данные, полученные в физическом эксперименте, проведенном в работе , c численными расчетами, проведенными в работе . Кривые 1 и 2 являются интерполяций экспериментальных и численных данных сплайном второго порядка . Результаты физического эксперимента хорошо согласуются с результатами расчетов численной модели, что демонстрирует её работоспособность.
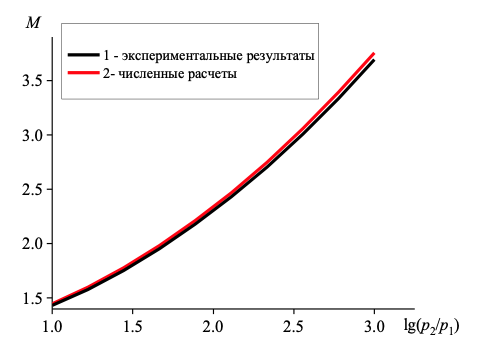
Рисунок 1 - Сопоставление числа Маха фронта ударной волны в газовзвеси
Примечание: кривая 1 построена обработкой экспериментов в работе [17], кривая 2 – результат численных расчетов
3. Результаты расчетов
В расчетах моделировалось течение в запыленной среде — воздухе с взвешенными твердыми частицами имеющими физическую плотность кварцевого песка. Параметры дисперсной фазы, физическая плотность материала — ρ10=2500 кг/м3, размер дисперсных включений — d=2 мкм, начальная объемная доля дисперсной фазы α0=0,001. Продольная длина канала — L= 1 м, размер канала в поперечном направлении — h=0,1 м. Количество узлов в х направлении — Nx=300, количество узлов в направлении у — Ny=60. Давление газа в камере высокого давления — р2=200 кПа, давление газа в камере низкого давления — р1=100 кПа – рисунок 2.
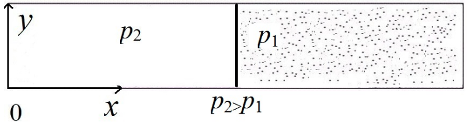
Рисунок 2 - Общая схема ударной трубы с газовзвесью
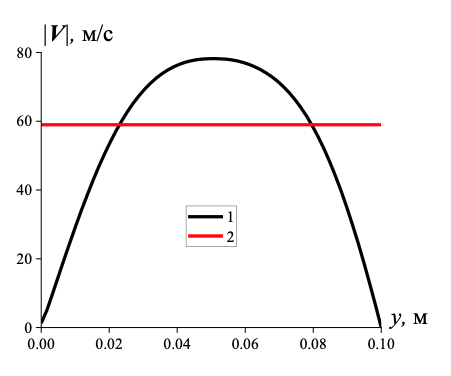
Рисунок 3 - Поперечное распределение модуля скорости газа для граничных условий Дирихле – 1, граничных условий Неймана – 2
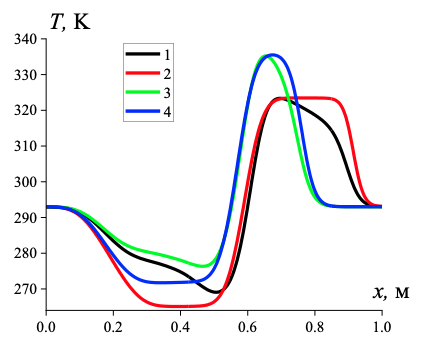
Рисунок 4 - Распределение температуры газа и несущей среды для различных граничных условий в трубе
Примечание: 1 − граничные условия Дирихле, однородный газ; 2 − граничные условия Неймана, однородный газ; 3 − граничные условия Дирихле, несущая среда газовзвеси; 4 − граничные условия Неймана, несущая среда газовзвеси
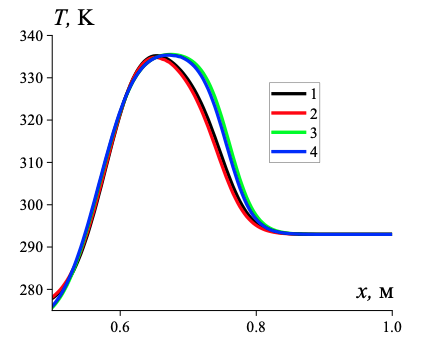
Рисунок 5 - Распределение температуры несущей среды газовзвеси и дисперсной фазы для различных граничных условий в трубе
Примечание: граничные условия Дирихле: 1 − несущая среда; 2 − дисперсная фаза, однородный газ; граничные условия Неймана: 3 − несущая среда; 4 − дисперсная фаза
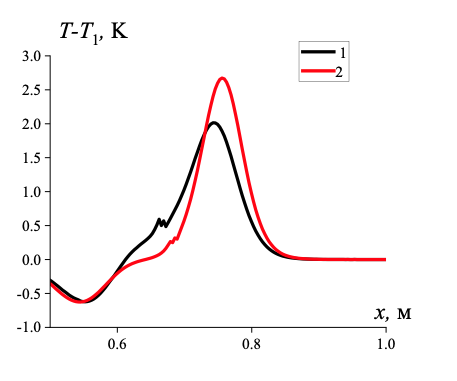
Рисунок 6 - Распределение разности температур несущей среды и дисперсной фазы
Примечание: 1 − граничные условия Дирихле; 2 − граничные условия Неймана
При задании граничных условий Неймана скорость распространения возмущения выше, разность температур несущей и дисперсной фазы отличается в большей степени, чем при граничных условий Дирихле — рисунок 6.
При моделировании распространения ударной волны с граничными условиями Неймана в однородном газе наблюдается большая скорость распространения ударной волны, чем при моделировании течения с граничными условиями Дирихле.
4. Заключение
В статье рассмотрены ударноволновые течения однородного газа и газовзвеси в канале. Математическая модель течения однородного газа и газовзвеси учитывала вязкость газа. При этом математическая модель позволяла учесть воздействие дисперсной фазы на течение газа. Целью работы было определить влияние выбора граничных условий на процесс моделирования работы ударно-волновой трубы. Выявлено, что для однородных граничных условий Дирихле, которые в большей степени соответствуют процессу движения ударной волны в канале, наблюдается меньшая скорость распространения ударной волны, а также меньшая величина параметров «температурного скольжения» фаз неоднородной среды. Результаты могут быть применены при моделировании ударноволновых течений газовзвесей в каналах и трубах.
