Development of Calculation Model of Modified Metal-Polymer Radial Bearing with Regard to Pressure and Temperature Dependence of Viscosity
Development of Calculation Model of Modified Metal-Polymer Radial Bearing with Regard to Pressure and Temperature Dependence of Viscosity
Abstract
The article is devoted to the development and analysis of a model of the movement of a micropolar lubricant in the working gap of a radial plain bearing with a fluoroplastic-containing antifriction composite polymer coating and with a groove on the supporting surface.
New models are obtained on the basis of classical equations in the “thin layer” approximation and the continuity equation, which describe the turbulent mode of motion of a lubricant with micropolar rheological properties. The results of the numerical analysis of the obtained models of existing operational characteristics made it possible to obtain a quantitative assessment of the effectiveness of the support profile with a fluoroplastic-containing antifriction composite polymer coating with an axial groove.
To complete the complex of studies and verify theoretical developments, experimental studies were carried out.
The novelty of the work lies in the concretization of the technique of engineering calculations for the design of an effective radial bearing with an antifriction polymer coating with an axial groove on the bearing surface of the bearing bush, taking into account the dependence of the rheological properties of a micropolar lubricant on pressure and temperature in a turbulent mode, which makes it possible to estimate the value of the main operational characteristics: hydrodynamic pressure, load ability and coefficient of friction, as well as to expand the scope of practical application of models for engineering calculations.
Thus, the design of a radial bearing with a polymer-coated support profile, a groove 3 mm wide, ensured a stable ascent of the shaft on a hydrodynamic wedge, which experimentally confirmed the correctness of the results of theoretical studies of a radial bearing with a diameter of 40 mm at a sliding speed of 0.32-3 m/s, load 4.9-24.5 MPa.
1. Введение
Подшипники скольжения должны обладать высокой износостойкостью и теплостойкостью. Работа гидродинамических подшипников скольжения зависит от режимов эксплуатации, толщины смазочного слоя между трущимися поверхностями радиального подшипника, а также от давления, от температуры смазочной среды в рабочем зазоре, расхода смазки. Для снижения потерь на трение в трибосистеме применяются высокотехнологичные смазочные материалы.
Для решения поставленной задачи проводится интегрирование системы безразмерных уравнений Навье – Стокса для «тонкого слоя» и уравнения неразрывности. Разработаны математические модели движения жидкого смазочного материала в рабочей зоне радиального подшипника скольжения с учетом реологических свойств применяемого смазочного материала.
В работе M. Deligant и др. рассматривается теоретическая модель для расчета потери мощности на трение в подшипниках скольжения. Результаты теоретических и экспериментальных исследований хорошо согласовываются, что и позволило прогнозировать величину потери на трение.
Также выявлено понижение температуры за счет хорошей теплопроводности подшипника.
В статье E. Zadorozhnaya и др. представлено исследование подшипников турбокомпрессора. Предложены многослойные подшипники с плавающими кольцами. Для амплитуды вращения ротора и температуры подшипника получены уравнения регрессии. Указано, что при любом режиме работы ротора амплитуда прецессии ротора составляет менее 11 мкм, а это указывает на отсутствие контакта ротора и колец радиального подшипника. Температура в подшипнике в зависимости от подачи смазочного материала повышается незначительно.
В работе S. C. Sharma и др. проводятся теоретические исследования статических и динамических характеристик гибридного подшипника со щелевым вводом смазочного материала. Отмечено, что существенно влияет на эксплуатационные характеристики гибридных подшипников изменение вязкости из-за повышения температуры смазочной жидкости.
Исследование B. Kucinsсhi и M. Fillon направлено на изучение распределения температуры при переходных тепловых периодах. Отмечено, что скорость вращения вала, нагрузка в зоне трения влияют на температуру смазочного слоя и момент жидкостного трения. При повышении скорости вращения вала температура значительно возрастает, также температура будет выше при небольших нагрузках, чем при более высоких, из-за рециркуляции смазки.
В работе P. Khatak и H. Garg проведено исследование гибридного подшипника скольжения на микрополярной смазке. Авторами сделан вывод, что на работу подшипника скольжения существенно влияет повышение температуры в зоне трения. Численный анализ решения задачи показывает: чтобы получить реалистические характеристики подшипника скольжения, работающего с микрополярной смазкой, необходимо учитывать тепловые эффекты в зоне трения.
В. Н. Прокопьев и др. , , провели расчет устойчивости термогидродинамических сложнонагруженных опор скольжения и подшипников скольжения. Анализировались теплонапряженность, износостойкость, долговечность.
В работах Н. П. Старостина и др. , решаются задачи определения нестационарного температурного поля самосмазывающихся радиальных подшипников скольжения из антифрикционного материала. Определена математическая модель для диагностики трения. Сделан вывод: распределение температуры по длине вала и опоры однородно. Получены основные соотношения для тепловой диагностики трения.
Авторами работ , , , проведены исследования радиальных, сферических и упорных подшипников скольжения. Рассмотрена задача о распределении температуры в области соприкосновения поверхностей вала и подшипниковой втулки. В разработанных математических моделях анализируются тепловые потоки через контактную поверхность полимерного и металлополимерного подшипников. Получены формулы для нахождения температурного поля в подшипнике скольжения с учетом постоянства коэффициента разделения теплового потока в зоне трения.
Д. С. Коднир и др. , представили эластогидродинамическую теорию смазки. Эластогидродинамическая смазка дает возможность более точно получать расчет тепловыведения в смазочном слое при определении силы трения, толщины пленки смазочного материала, тепловой мощности работы подшипников скольжения.
В работах , , , авторами используются эмпирические зависимости от параметров исследуемых пар трения, смазочных материалов и от эксплуатационных условий подшипников скольжения, которые могут быть использованы при расчете температурных полей в зоне трения.
Из проведенного анализа исследований видно, что необходимо повышать точность имеющихся математических моделей, а также разрабатывать новые математические модели при исследовании работы подшипников скольжения с учетом конструкторских их особенностей и с учетом реологических свойств применяемого смазочного материала.
В данной работе приводится исследование модели движения жидкого смазочного материала в радиальном подшипнике скольжения с осевой канавкой в подшипниковой втулке, имеющей полимерное покрытие её рабочей поверхности.
2. Постановка задачи
Рассмотрим турбулентное движение вязкого несжимаемого смазочного материала между эксцентрично расположенными круговым шипом (валом) радиусом и подшипниковой втулкой радиусом
. Смазочный материал заполняет всё пространство между ними.
Для решения задачи предположим, что подшипниковая втулка находится в покое, а вал вращается вокруг своей неподвижной оси с постоянной угловой скоростью . На рабочую поверхность подшипниковой втулки нанесено полимерное покрытие. Опорная поверхность подшипниковой втулки содержит осевую канавку для подачи смазочного материала в зону трения.
Решение задачи проведем в полярной системе координат с началом в центре подшипниковой втулки и углом
(рис. 1). Уравнения контура вала, подшипниковой втулки, осевой канавки запишем в виде:
где
– радиус вала;
– радиус подшипниковой втулки;
– высота канавки;
– эксцентриситет;
– относительный эксцентриситет.
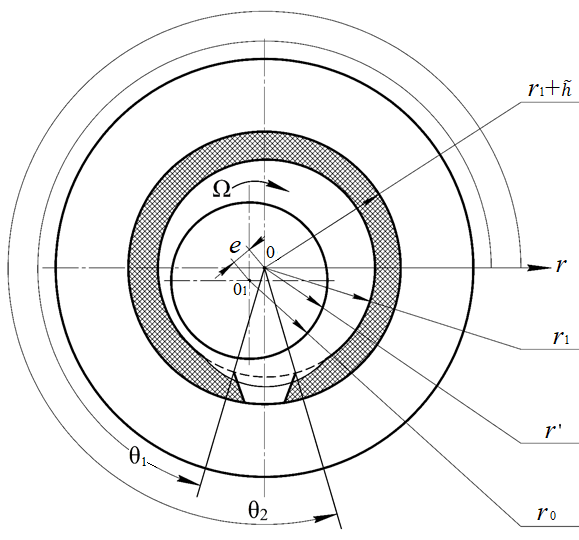
Рисунок 1 - Расчетная схема
Введем коэффициент для турбулентности в смазочном слое:
где
где – характерная вязкость;
– коэффициент динамической вязкости смазочного материала;
– гидродинамическое давление в смазочном слое;
,
– постоянная экспериментальная величина;
– температура.
Запишем уравнения движения смазочного материала – вязкой несжимаемой жидкости в «тонком слое» и уравнение неразрывности
где ,
– компоненты вектора скорости смазочного материала, при следующих граничных условиях:
где – давление на торцах интервала.
Перейдем к безразмерным величинам:
Дальнейшее решение (3) и (4) проведем с учетом (5) и получим:
где – конструктивный параметр;
– конструктивный параметр, характеризующий канавку;
и
– соответственно угловые координаты канавки;
и
– функции, полагающие наличие полимерного покрытия на рабочей поверхности подшипниковой втулки.
При решении задачи учтем условие постоянства расхода смазочного материала в единицу времени в любом сечении
а также условие непрерывности гидродинамического давления в окрестности канавки
Запишем соотношения для определения функций и
:
Учитывая (7), (8), (9), будем искать автомодельное решение поставленной задачи (6) в виде:
Выполнив подстановку (10) в (6), получим:
Запишем граничные условия для решения системы (11):
Учитывая (12), для записи поля скоростей проинтегрируем систему уравнений (11):
определяется из уравнения
:
определим из условия
:
где .
Гидродинамическое давление определим из уравнения:
Из уравнения (16) определим функцию , используя закономерность изменения скорости диссипации энергии смазочной среды:
Влияние температуры на реологические свойства смазочного материала определяется выражением:
где – теплоемкость при постоянном давлении;
– толщина масляной пленки;
– расход смазочного материала в единицу времени:
Выражение продифференцируем по
:
Определим с учетом (16):
Непосредственным интегрированием (21) получим:
где
Найдем аналитические выражения для из системы уравнений (22) с точностью
,
,
,
,
,
,
,
,
включительно:
Учитывая (16) и (23), получим аналитические выражения для определения безразмерного гидродинамического давления:
Для определения несущей способности и силы трения используем формулу (24):
По полученным аналитическим выражениям для гидродинамического давления в смазочном слое (24), несущей способности
,
(25) при численных значениях рассматриваемых параметров: скорость 1 м/с,
= = 5,74–22,92 град,
= 4,9–24,5 МПа,
= 0,0707–0,0076 Нс/м2,
= 100–2400 с–1,
= 0–1,
= 25–100 °С,
= 0,05·10–3–0,07·10–3 м,
= 0,01995–0,04993 м,
= 0,2 МПа, построены графики (рис. 2, 3) зависимостей при постоянной угловой скорости вращения вала вокруг своей оси.
На рис. 2 приведен график изменения радиальной составляющей несущей способности в зависимости от применяемой нагрузки, скоростных режимов и от параметров осевой канавки.
Из анализа функциональной зависимости для сделан вывод, что осевая канавка слабо влияет на гидродинамический режим работы исследуемого подшипника. В то же время предложенная осевая канавка в расчетной модели обеспечивает формирование гидродинамического давления с учетом влияния температуры на реологические свойства смазочного материала.
На работу полимерной трибосистемы, на свойства полимерного покрытия рабочей поверхности подшипниковой втулки существенно влияет температура радиального подшипника скольжения.
Численный анализ полученных теоретических результатов позволил рассчитать несущую способность, коэффициент трения (табл. 1) от нагрузки, вязкости смазочного материала, от давления в смазочном слое, температуры маслоподдерживающей осевой канавки и от её ширины.
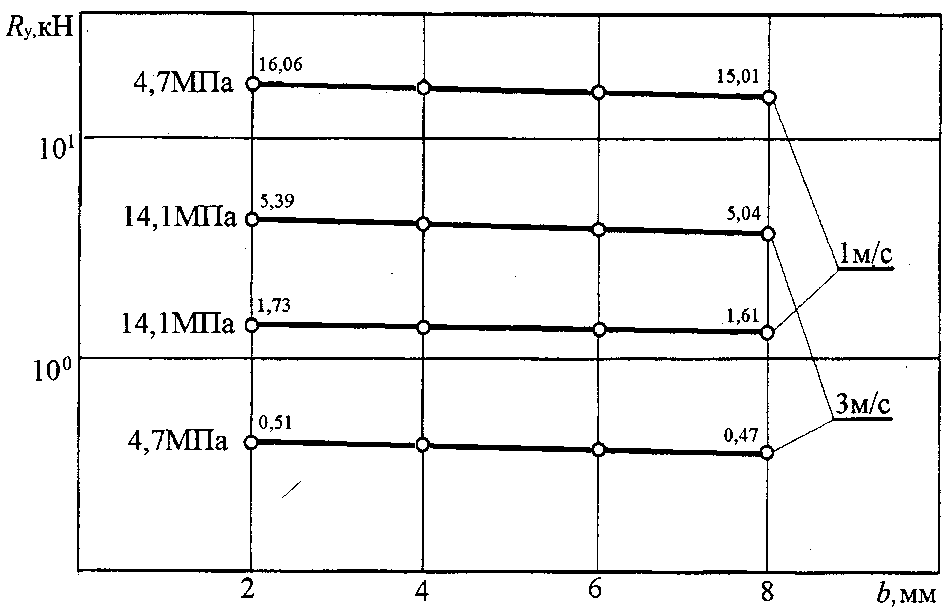
Рисунок 2 - Изменение радиальной составляющей несущей способности
Таблица 1 - Зависимость коэффициента трения от нагрузки
Коэффициент трения | Нагрузка σ, МПа | Ширина маслоподдерживающей канавки b, мм | ||||
1 | 2 | 3 | 4 | 5 | ||
f | 0,2 | 0,01402 | 0,01395 | 0,01388 | 0,01381 | 0,01375 |
4,7 | 0,000596 | 0,000594 | 0,000891 | 0,000488 | 0,00585 | |
14,1 | 0,0001987 | 0,0001979 | 0,0001969 | 0,0001959 | 0,000195 | |
По анализу полученной зависимости для коэффициента трения от нагрузки в исследуемом диапазоне видим, что коэффициент трения находится в пределах гидродинамического режима работы радиального подшипника скольжения. Отмечается, что величина коэффициента трения не зависит от ширины осевой канавки.
По результатам численного анализа полученных зависимостей построены графики, приведенные на рисунке 3.
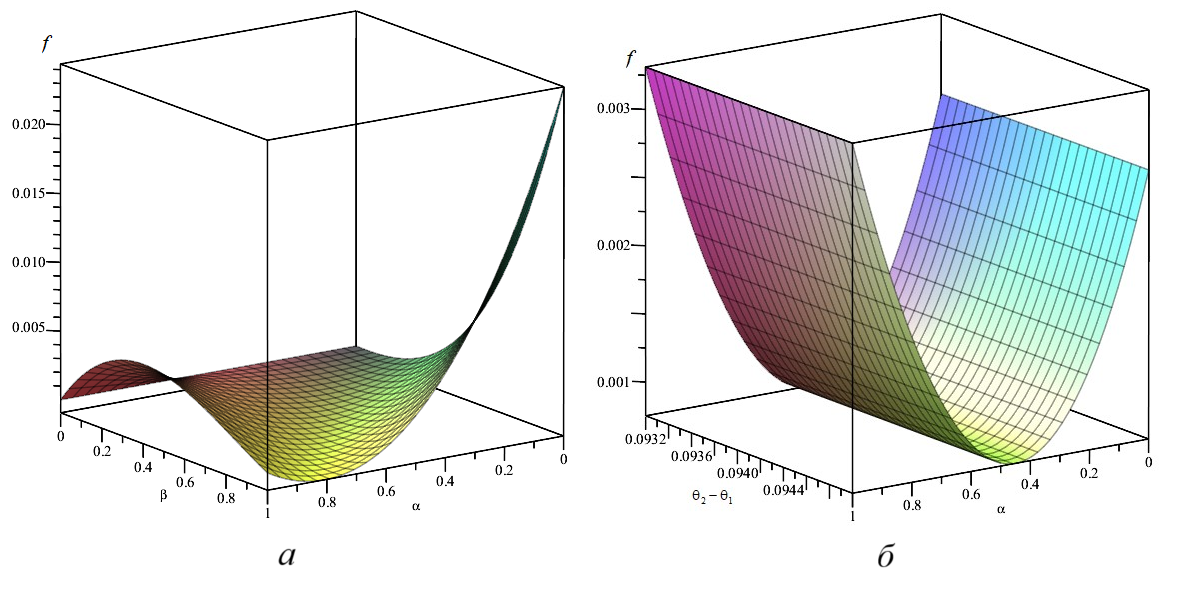
Рисунок 3 - Зависимость коэффициента трения от параметров:
а – вязкости смазочного материала от давления и температуры; б – характеризующих зависимость ширины осевой канавки и вязкости смазочного материала от температуры
3. Проведение экспериментов
Экспериментальные исследования проведены для новой конструкции радиальных подшипников, включающих в себя полимерное покрытие опорной поверхности подшипниковой втулки и имеющуюся в ней осевую канавку.
Триботехнические исследования проводились на модернизированной машине трения ИИ 5018 (рис. 4, 5).
Определялась объемная температура в паре трения «ролик – колодка» (рис. 4) с фторопластсодержащим композиционным полимерным покрытием рабочей поверхности колодки.
Объемная температура определялась по показаниям тепловизора (рис. 5).

Рисунок 4 - Определение объемной температуры в паре трения «ролик – колодка»:
1, 2 – термопары
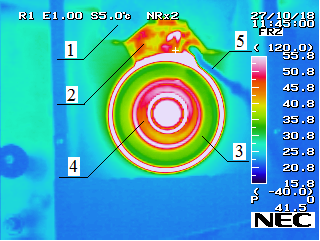
Рисунок 5 - Показания тепловизора при определении объемной температуры в паре трения «ролик – колодка» с фторопластсодержащим композиционным полимерным покрытием:
1 – колодкодержатель; 2 – опытный образец; 3 – ролик; 4 – контргайка; 5 – термопара
4. Результаты исследований
В результате теоретического исследования установлено, что несущая способность повышается примерно на 12–14 %, а коэффициент трения снижается на 8–10% в диапазоне исследованных режимов (табл. 2).
Таблица 2 - Результаты теоретического исследования поверхности подшипниковой втулки с фторопластсодержащим композиционным полимерным покрытием
№ | σ, МПа | Угловые координаты (θ2 – θ1) | ||||
5,74 | 10,03 | 14,32 | 18,61 | 22,92 | ||
Коэффициент трения | ||||||
1 | 4,9 | 0,008890 | 0,0112130 | 0,009200 | 0,0060000 | 0,00333000 |
2 | 9,8 | 0,005590 | 0,0055910 | 0,005753 | 0,0040850 | 0,00269650 |
3 | 14,7 | 0,002293 | 0,0023920 | 0,002306 | 0,0021705 | 0,00205700 |
4 | 19,6 | 0,002195 | 0,0022613 | 0,002204 | 0,0021136 | 0,00203793 |
5 | 24,5 | 0,002097 | 0,0021307 | 0,002102 | 0,0020570 | 0,00201887 |
В процессе экспериментального исследования были установлены области рационального применения полученных моделей. Получен устойчивый гидродинамический режим трения после 2-минутной приработки, при этом нагрузка увеличивалась ступенчато 5 раз от 4,9 до 24,5 МПа (табл. 3).
Таблица 3 - Результаты исследования поверхности подшипниковой втулки с фторопластсодержащим композиционным полимерным покрытием
№ | Режим | Коэффициент трения | Погрешность, % | |||||
σ, МПа | V, м/с | Теоретический результат | Экспериментальное исследование | |||||
Полимерное покрытие | Покрытие в канавке | Покрытие | Покрытие с канавкой | |||||
1 | 4,9 | 0,3 | 0,0115 | 0,0097 | 0,0139 | 0,0114 | 5–12 | 6–13 |
2 | 9,8 | 0,3 | 0,0060 | 0,0043 | 0,0074 | 0,0042 | ||
3 | 14,7 | 0,3 | 0,0040 | 0,0021 | 0,0053 | 0,0033 | ||
4 | 19,6 | 0,3 | 0,0055 | 0,0031 | 0,0077 | 0,0052 | ||
5 | 24,5 | 0,3 | 0,0095 | 0,0064 | 0,0107 | 0,0078 | ||
5. Обсуждение результатов
Теоретически решена задача гидродинамического расчета радиального подшипника скольжения, имеющего полимерное покрытие и осевую канавку на рабочей поверхности подшипниковой втулки. Установлены необходимые параметры канавки, позволяющие подшипнику выходить в гидродинамический режим при заданной нагрузке.
Исследованная новая конструкция радиального подшипника позволила выявить, что при работе нового подшипника в канавке возникает циркуляционное течение смазки, позволяющее образовывать гидродинамический клин, что приводит к повышению несущей способности подшипника. Разработана расчетная модель течения смазки в рабочем зазоре радиального подшипника, учтена зависимость вязкости смазки от давления и температуры.
При наличии на рабочей поверхности подшипниковой втулки осевой канавки протяженность рабочей зоны гидродинамического давления значительно возрастает, что приводит к увеличению несущей способности подшипника.
Выполненные экспериментальные исследования позволили подтвердить полученные теоретические результаты и установить, что нанесенное полимерное покрытие и наличие осевой канавки на рабочей поверхности подшипниковой втулки повышают работоспособность радиального подшипника скольжения, увеличивая срок его эксплуатации, при применении смазочного материала с учетом реологических свойств этого материала.
Новый способ расчетных моделей позволяет значительно расширить область применения работы радиальных подшипников.
6. Заключение
1. Проведены теоретическое и экспериментальное исследования радиальных подшипников скольжения с фторопластсодержащим полимерным покрытием и с осевой канавкой на опорной поверхности подшипниковой втулки.
2. Полученные расчетные математические модели учитывают в качестве дополнительной смазки фторопластсодержащее покрытие и осевую канавку на опорной поверхности подшипниковой втулки.
3. В результате исследования с учетом реологических свойств смазочного материала разработаны новые математические методы прогнозирования работы радиальных подшипников скольжения, обеспечивающие одновременно повышенную несущую способность и гидродинамическую устойчивость их работы.
4. В диапазоне исследуемых режимов работы радиальных подшипников скольжения с осевой канавкой шириной 3 мм установлено повышение их несущей способности на 12–14% и снижение коэффициента трения на 8–10%.
5. Конструкция радиального подшипника с полимерным покрытием и осевой канавкой шириной 3 мм повышает работоспособность подшипника за счет лучшего поступления смази в зону трения.
Условные обозначения:
r0 – радиус вала; r1 – радиус подшипниковой втулки; – высота канавки; e – эксцентриситет; ε – относительный эксцентриситет; μ0 – характерная вязкость; μ' – коэффициент динамической вязкости смазочного материала; p' – гидродинамическое давление в смазочном слое; α', β' – постоянная экспериментальная величина; T' – температура; I – механический эквивалент тепла; λ – теплопроводность смазочного материала;
– конструктивный параметр;
– конструктивный параметр, характеризующий канавку; θ1, θ2 – соответственно угловые координаты канавки; u*(θ) и v*(θ) – известные функции, обусловленные наличием полимерного покрытия на поверхности подшипниковой втулки; Q – расход смазочного материала в единицу времени; Cр – теплоемкость при постоянном давлении; h(θ) – толщина масляной пленки.
