DISTRIBUTIVE METHOD FOR A TASK ABOUT ASSIGNMENTS
Сдвижков О. А.
Кандидат физико-математических наук, Российский государственный университет туризма и сервиса
РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД ДЛЯ ЗАДАЧИ О НАЗНАЧЕНИЯХ
Аннотация
Задача о назначениях, которая есть частный случай транспортной задачи, имеет много приложений в экономике. Поэтому изучение методов решения задачи о назначениях является актуальной проблемой. В статье рассматриваются циклы пересчета допустимых планов задачи о назначениях, оценки циклов пересчета, оценки строк и столбцов допустимых планов, критерии оптимальности и метод решения задачи о назначениях. Этот метод опирается на оценки циклов пересчета и оценки строк и столбцов допустимых планов. Имеется подробно разобранный пример. Кроме того, распределительный метод решения задачи о назначениях применяется к задаче коммивояжера.
Ключевые слова: цикл, стоимость, оптимальность.Sdvizhkov O. A.
PhD in Physics and Mathematics, Russian state university of tourism and service
DISTRIBUTIVE METHOD FOR A TASK ABOUT ASSIGNMENTS
Abstract
The task about assignments, which is a special case of a transport task, has many appendices in economy. Therefore, study of methods of the decision of a task about assignments is an urgent problem. The article considers cycles of recalculation of the allowable plans of a task about assignments, estimations of cycles of recalculation, estimations of rows and columns of the allowable plans, criteria of an optimality and the method of the decision of a task about assignments. This method bases on estimations of cycles of recalculation and estimation of rows and columns of the allowable plans. There is an in detail disassembled example. Moreover, the distributive method of the decision of a task about assignments applies to travelling salesman problem.
Keywords: cycle, cost, optimality.1. Оценки циклов пересчета
Будем рассматривать задачу о назначениях [2] как задачу нахождения по заданной матрице стоимостей выполнения n исполнителями n видов работ ![]() , такого плана распределения исполнителей по работам, при котором суммарная стоимость выполнения всех работ является минимальной. Предполагается, что каждый исполнитель выполняет только одну работу и каждая работа выполняется только одним исполнителем.
, такого плана распределения исполнителей по работам, при котором суммарная стоимость выполнения всех работ является минимальной. Предполагается, что каждый исполнитель выполняет только одну работу и каждая работа выполняется только одним исполнителем.
В двоичных (булевых) переменных ![]() , когда
, когда ![]() =1, если i-му исполнителю поручается j-ая работа, и
=1, если i-му исполнителю поручается j-ая работа, и ![]() =0, в противном случае, задача о назначениях сводится к задаче линейного программирования:
=0, в противном случае, задача о назначениях сводится к задаче линейного программирования:
![]() (1)
(1)
![]() (2)
(2)
Двоичные планы Χ=(![]() ), удовлетворяющие (2), будем называть допустимыми.
), удовлетворяющие (2), будем называть допустимыми.
Первоначальный допустимый план Х можно получить как методом северо-западного угла, принимая ![]() =1, так и методом наименьших стоимостей. Он будет вырожденным, поскольку в нем не нулевых значений n, а ранг системы (2) равен 2n-1.
=1, так и методом наименьших стоимостей. Он будет вырожденным, поскольку в нем не нулевых значений n, а ранг системы (2) равен 2n-1.
Пусть ![]() =0, γ – означенный цикл [1, стр. 242], связывающий переменные:
=0, γ – означенный цикл [1, стр. 242], связывающий переменные:
![]() (3)
(3)
Так как значения не нулевых переменных в (3) равны 1, то сдвиг [1, стр. 243] на величину ![]() по циклу (3) приводит к допустимому плану Х* только, если
по циклу (3) приводит к допустимому плану Х* только, если
![]()
Δγ – оценка цикла пересчета γ, вычисляемая по формуле
![]() – сумма стоимостей, соответствующих элементам цикла γ, имеющим значение 0 (1). Следовательно, справедлива теорема.
– сумма стоимостей, соответствующих элементам цикла γ, имеющим значение 0 (1). Следовательно, справедлива теорема.
Теорема 1. Если все оценки Δγ в допустимом плане Х задачи о назначениях удовлетворяют условию Δγ≥0, то план Х оптимальный.
2. Оценки строк и столбцов допустимых планов
Простейшие циклы пересчета задачи о назначениях имеют четыре вершины, в которых значения 0 и 1 чередуются. Нетрудно, перебирая такие циклы и начиная перебор заново, если план был улучшен, получить допустимый план ![]() , в котором оценки всех 4-циклов пересчета неотрицательные.
, в котором оценки всех 4-циклов пересчета неотрицательные.
Перебор циклов пересчета, имеющих из шести и более вершин, может оказаться достаточно трудоемкой процедурой. Однако перебирать все такие циклы пересчета нет необходимости, достаточно ограничиться теми, которые проходят через переменные ![]() =0, для которых
=0, для которых ![]() – стоимости, соответствующие переменным, имеющим значение 1, поскольку только за счет таких стоимостей план можно улучшить.
– стоимости, соответствующие переменным, имеющим значение 1, поскольку только за счет таких стоимостей план можно улучшить.
Теорема 2. Если для цикла пересчета γ, расположенного в строках ![]() (столбцах
(столбцах ![]() ) допустимого плана Х задачи о назначениях, выполняется , то сумма оценок этих строк (столбцов) отрицательная.
) допустимого плана Х задачи о назначениях, выполняется , то сумма оценок этих строк (столбцов) отрицательная.
В силу теорем 1, 2 имеет место следующая теорема – критерий оптимальности плана Х, в котором есть строки (столбцы), сумма оценок некоторых отрицательная.
Теорема 3. Если в допустимом плане Х задачи о назначениях каждый набор r строк такой, что сумма оценок этих строк отрицательная, обладает тем свойством, что в нем нет 2r-цикла пересчета γ такого, что Δ(γ)<0, то план Х является оптимальным.
Аналогичная теорема имеет место для столбцов. 3. Распределительный метод для задачи о назначениях Из вышеизложенного вытекает следующий метод решения задачи о назначениях, который, естественно, назвать распределительным.- Составляется первоначальный допустимый план Х.
- Принимается r=1.
- Значение r увеличивается на 1.
- Если r>2, то вычисляются оценки строк и столбцов.
- В плане Х выбирается 2r-цикл пересчета γ, не имеющий оценки Δ(γ), который при r>2 расположен в строках (столбцах) сумма оценок которых отрицательна, если такого цикла нет, но r<n, то на шаг 3, иначе останов – план Х является оптимальным.
- Вычисляется оценка Δ(γ).
- Если Δ(γ)≥0, то на пункт 5, иначе на пункт 8.
- Значения переменных в цикле γ заменяются их отрицаниями, полученный план принимается за текущий план Х и на шаг 2.
Замечание. Текущие планы можно указывать в матрице С, выделяя стоимости, соответствующие переменным плана, имеющим значение 1, например, заключением их в круглые скобки. В этом случае циклы пересчета также указываются в матрице С.
Пример. Решить задачу о назначениях, применяя распределительный метод:
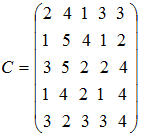

Начинаем перебор 4-циклов, так как 2+5>1+4, то план можно улучшить, выбирая в цикле ![]() другую пару стоимостей, что дает:
другую пару стоимостей, что дает:

Снова начиная перебор, приходим к соотношению 4+4>2+3, позволяющему улучшить план:

Теперь улучшить план с помощью 4-циклов нельзя, нужно рассматривать циклы с большим числом вершин. Находим оценки строк и столбцов данного плана:
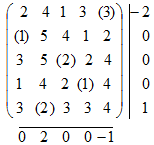
Оценки столбцов показывают, что второй столбец надо исключить из рассмотрения. После этого нетрудно заметить, что цикл пересчета, приводящий к улучшенному плану, так как 1+2+1+1<3+1+1+2, имеет вид:
![]()
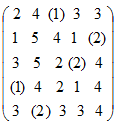
Улучшить этот план 4-циклами пересчета нельзя, выписываем оценки строк и столбцов:
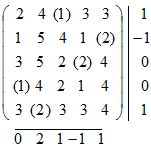
Оценки столбцов показывают, что улучшение плана возможно только за счет цикла пересчета, расположенного в 1-м и 4-м столбцах, но в них есть только один цикл пересчета ![]() , которым, так как 3+1>1+1, улучшить план нельзя. Следовательно, последний план является оптимальным.
, которым, так как 3+1>1+1, улучшить план нельзя. Следовательно, последний план является оптимальным.
Задача коммивояжера [2] – задача нахождения замкнутого маршрута минимальной длины, по которому коммивояжер (бродячий торговец) может объехать n населенных пунктов, расстояния между которыми заданы матрицей ![]() . Предполагается, что каждый из n пунктов он посещает только один раз.
. Предполагается, что каждый из n пунктов он посещает только один раз.
Математическая модель задачи коммивояжера [2] также имеет вид (1, 2), но есть дополнительное условие, состоящее в односвязности плана Х. Поэтому, если под циклами пересчета понимать такие циклы пересчета (3, 4), которые переводят односвязный план Х в односвязный план Х*, то распределительный метод данного пункта можно применять к задаче коммивояжера.
Пример. Решить задачу коммивояжера, применяя распределительный метод:
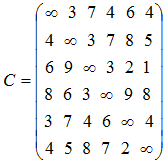

Перебирая 4-циклы, приходим к соотношению 3+9>3+8, то есть план можно улучшить, но пересчет по циклу ![]() приводит к распадающемуся маршруту 1→2→5 →6→1, 3→4→3. Поэтому этот цикл из рассмотрения исключаем. По этой же причине исключаем из рассмотрения цикл
приводит к распадающемуся маршруту 1→2→5 →6→1, 3→4→3. Поэтому этот цикл из рассмотрения исключаем. По этой же причине исключаем из рассмотрения цикл ![]() , несмотря на то, что 4+9>2+8. В результате приходим к тому, что с помощью 4-циклов пересчета улучшить первоначальный план нельзя, переходим к 6-циклам.
, несмотря на то, что 4+9>2+8. В результате приходим к тому, что с помощью 4-циклов пересчета улучшить первоначальный план нельзя, переходим к 6-циклам.
Наибольшее положительное значение разность ![]() принимает для стоимостей
принимает для стоимостей ![]() . Составляем 6-цикл, содержащий, например,
. Составляем 6-цикл, содержащий, например, ![]() :
:
![]()
Так как 3+3+9>7+2+3 и пересчет по циклу приводит к односвязному маршруту, то переходим к новому улучшенному плану:

получаем 2+4+4>1+2+3, причем пересчет по циклу приводит к односвязному маршруту. Поэтому переходим к новому улучшенному плану:

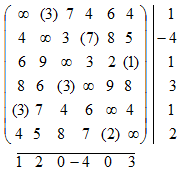
Из оценок столбцов следует, что цикл пересчета, улучшающий план, может находиться или в первых 5 столбцах, или в последних 4 столбцах, но анализ показывает, что таких циклов в наборах этих столбцов нет. Поэтому последний план является оптимальным.
Ответ: 1→2→4 →3→6→5→1, zmin=19.Литература
- Карпелевич Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.: Физматгиз, 1963. – С. 232-262.
- Сдвижков О.А. Практикум по методам оптимизации. – М.: Вузовский учебник: ИНФРА-М, 2015. – С. 45-95.
References
- Karpelevich F.I., Sadovskij L.E. Jelementy linejnoj algebry i linejnogo programmirovanija. – M.: Fizmatgiz, 1963. – S. 232-262.
- Sdvizhkov O.A. Praktikum po metodam optimizacii. – M.: Vuzovskij uchebnik: INFRA-M, 2015. – S. 45-95.
