DETERMINING THE SPEED OF GAS FLOW IN THE SHELLS OF RED GIANTS ON THE RESONANT BROADENING OF HYDROGEN LINES

Лысенко В.Е.¹, Иванов В.А.², Иванов А.Л.³

¹Аспирант, ²Аспирант, ³ Преподаватель, Кубанский государственный университет

ОПРЕДЕЛЕНИЕ СКОРОСТИ ДВИЖЕНИЯ ГАЗА В ОБОЛОЧКАХ КРАСНЫХ ГИГАНТОВ ПО РЕЗОНАНСНОМУ УШИРЕНИЮ ВОДОРОДНЫХ ЛИНИЙ

Аннотация

В статье рассмотрен метод определения абсолютной пространственной скорости движения газа и его концентрации в оболочках красных гигантов на основе анализа профиля водородной линии H_α, с учетом резонансного уширения спектральных линий. Линию водорода можно представить, как суперпозицию тепловых профилей, центральная частота которых хаотически меняется в некоторых пределах межатомными взаимодействиями. Определены абсолютные пространственные скорости газа и его концентрация для оболочек 20 красных гигантов. Абсолютные пространственные скорости газа лежат в пределах от 7500 до 14500 м/с. Концентрации находятся в пределах (6,8–8,5) 10²³ м^–3.

Ключевые слова: оптика движущихся сред, резонансное уширение спектральных линий, оболочки красных гигантов.

Lysenko V.E.¹, Ivanov V.A.², Ivanov A.L.³

¹Postgraduate student, ²Postgraduate student, ³Assistant lecturer, Kuban State University

DETERMINING THE SPEED OF GAS FLOW IN THE SHELLS OF RED GIANTS ON THE RESONANT BROADENING OF HYDROGEN LINES

Abstract

The article describes the method for determining the absolute spatial speed of the gas and its concentration in the shells of the red giants on the basis of the analysis of the profile of the H_α-line of hydrogen, taking into account of the resonance broadening of spectral lines. Line of hydrogen can be represented as a superposition of thermal profiles, the central frequency of which randomly varies in some limits by interatomic interactions. The absolute spatial velocity of the gas and its concentration for shells of 20 red giants is defined. The absolute spatial velocity of the gas are in the range from 7500 to 14500 m/s. Concentrations are in the range of (6.8–8.5) 10²³ m^–3.

Keywords: optics of moving media, resonant broadening of spectral lines, shells of red giants.

Оболочки звезд являются примерами систем, где следует учитывать эффекты оптики движущихся сред. Одним из таких эффектов является уширение спектральных линий вследствие эффекта Доплера не только при тепловом движении атомов, но и при движении газовых масс. Определение кинетических характеристик газа в оболочках звезд путем анализа профиля спектральных линий стало возможным по мере повышения разрешения спектральных приборов.

Цель данной работы — разработать метод учета движения газа при резонансном уширении путем анализа профиля спектральной линии, а также определить абсолютную пространственную скорость движения газовых масс и концентрацию газа в оболочке красных гигантов на основе анализа профиля линии водорода H_α 6563 Å.

В период, когда спектральные приборы не имели высокого разрешения, были разработаны методы определения кинетических характеристик движущейся среды на основе распределения Фойгта, в котором параметром выступает полуширина спектральной линии, а также посредством кривых роста. Так Т. С. Галкиной в Крымской астрофизической обсерватории были определены турбулентные скорости газовых масс в оболочках сверхгигантов, они составили по анализу разных линий от 7 до 30 км/с. [1]

Согласно Д. Ф. Грею скорость турбулентности в оболочках гигантских звезд класса G5 III, определенная путем Фурье-анализа всех возможных линий в спектрах между 6122 Å и 6270 Å, составила порядка 7 км/с. [2] Им же отмечена зависимость скорости макротурбулентных движений газа в оболочках гигантских звезд от температуры. Дисперсия значений для большинства звезд от 7,0 км/с для G5 III до 4,6 км/с для K2 III. [3]

А. С. Брун и А. Паласиос по результатам математического моделирования однозначно связывают вращение ядра и турбулентность и указывают, что турбулентность в оболочках красных гигантов очень сильна, даже в случае медленного вращения ядра. [4]

Группа Х. Брунтта [5] получила спектры высокого разрешения красных гигантов для определения параметров их атмосфер таких, как эффективная температура, скорость микротурбуленции, скорость макротурбуленции, металличность. Для этого использовались изолированные линии металлов. Скорость макротурбулентных потоков по их измерениям составила от 1,5 до 5 км/с.

Для оболочек гигантских звезд следует учитывать межатомные взаимодействия — уширение эффектами давления. Чтобы учесть еще и скорость движения газа, следует выполнить свертку профиля, уширенного эффектами давления, и профиля, уширенного движением газа. При этом для удаленной уединенной звезды, спектр которой формируется всеми ее участками, отделить скорость вращения звезды в целом от относительной скорости газовых потоков в ее оболочке не представляется возможным.

Линии водорода бальмеровской серии образованы переходами со второго (уже возбужденного) уровня, который при межатомных взаимодействиях может существенно деформироваться в отличие от основного уровня, который слабо деформируется во внешних полях. Линию водорода в спектре звезды можно представить, как суперпозицию тепловых профилей отдельных линий, частота которых хаотически меняется в некоторых пределах межатомными взаимодействиями. Это составляет сущность резонансного уширения.

Чтобы описать ядро такой линии, будем учитывать только дальние пролеты атомов друг мимо друга, полагая концентрацию атомов достаточно малой. Диаметр атома водорода заменим на некоторый эффективный диаметр, на котором потенциал электронной оболочки в 1000 раз меньше, чем на поверхности сферы первого боровского радиуса. Эффективный диаметр атома водорода на основном уровне, рассчитанный таким образом, равен 32,4 Å. Примем, что большинство атомов находятся именно на основном уровне. Это значение необходимо для определения среднего времени свободного пробега атомов.

Сначала учтем турбулентное движение при тепловом профиле спектральной линии. При турбулентности возникают вихри, лучевые скорости масс газа в них подчиняются равномерному распределению. Вихрь можно представить как вращающийся цилиндр. Вследствие эффекта Доплера фотон, поглощающийся из континуума, будет иметь не лабораторную частоту ω₀, а ω′ (с ― скорость света в вакууме)

  (1)

где u —  лучевая скорость. Лучевая скорость u попадает в промежуток [–υ, υ], υ — линейная скорость образующей цилиндра.

Каждая точка вихря поглощает на частоте ω согласно распределению (максвелловская плотность вероятности умножена на плотность вероятности равномерного непрерывного распределения (2υ)^–1)

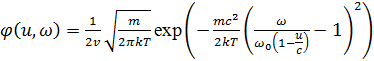  (2)

где m ― масса атома, k ― постоянная Больцмана, Т ― абсолютная температура. А вся вращающаяся поверхность излучает на частоте ω согласно распределению (плотность вероятности излучения фотонов со всей вращающейся поверхности)

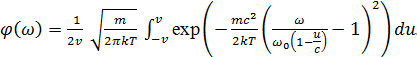  (3)

При детальном балансе вероятность поглощения равна коэффициенту поглощения. При малой скорости υ экспонента от нее зависеть практически не будет, она выносится за знак интеграла, а сам интеграл равен единице, поэтому при малых скоростях турбулентности полученный профиль переходит в тепловой.

Эту же последовательность действий необходимо совершить, чтобы учесть расширение турбулентным движением резонансно уширенных линий водорода.

Из принципа неопределенностей смещение частоты излучаемого или поглощаемого фотона в момент межатомного взаимодействия можно связать со средним временем между взаимодействиями τ (при этом можно утверждать, что неопределенность времени Δt не может быть больше среднего времени τ свободного пробега атома)

  (4)

которое из молекулярно-кинетической теории    (5)

где d ― эффективный диаметр атома, n ― концентрация атомов, m ― масса атома, k ― постоянная Больцмана, Т ― абсолютная температура.

Обозначим ω′ ― мгновенное смещение от центральной частоты ω₀, возникающее в результате хаотических взаимодействий с близкими атомами. Мгновенной центральной частотой теперь будет не ω₀, а ω₀+ω′. Максимальное значение модуля ω′ равно Δω. Тогда формула (3) для вероятности поглощения (коэффициент поглощения) фотона частоты ω при данных условиях примет вид

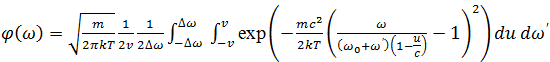(6)

В центре линии (ее глубина)

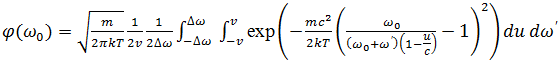(7)

Для расчета профиля линии при известной ее глубине имеем выражение

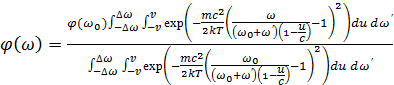  (8)

Следует иметь в виду, что скорость движения, определенная из анализа профиля линий, является величиной пространственно абсолютной, но определенной неточно, скорее некоторой характерной величиной. Кроме того, в данной задаче неизвестным параметром является концентрация атомов. Эффективную температуру звезд нужно считать известной и определять другими методами. Чтобы увидеть, среди каких пределов следует выбирать значения концентрации, построим профиль линии при равной нулю скорости движения газа. Результат показан на рисунке 1.

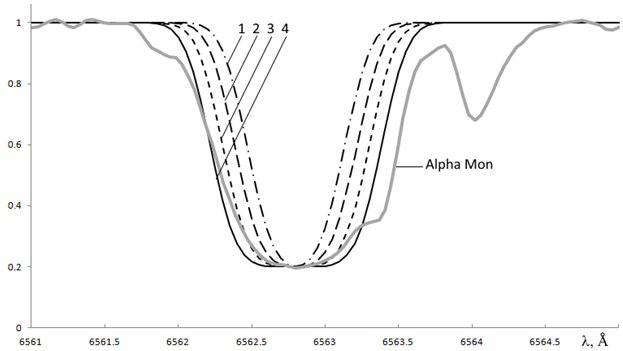
1 — 4·10²³ м^–3,  2 — 5·10²³ м^–3,  3 — 6·10²³ м^–3,  4 — 7·10²³ м^–3

Рис. 1 — Зависимость профиля линии H_α от концентрации, для сравнения приведен профиль этой же линии в спектре Alpha Mon, по вертикали даны значения коэффициента поглощения или относительный поток в нормированном спектре

Чтобы увидеть, как влияет скорость движения газа на профиль линии, и среди каких пределов следует выбирать ее значение, построим профиль линии при неизменной концентрации 7·10²³ м^–3 и разных скоростях. Результат показан на рисунке 2. Мы видим, что увеличение скорости движения газа приводит к расширению крыльев линии и сужению ее ядра.

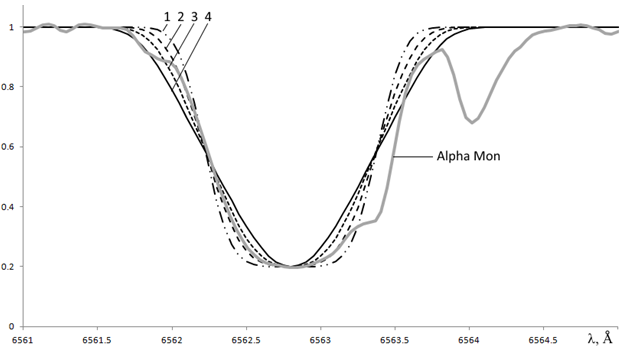
1 — 0,  2 — 5000 м/с,  3 — 10000 м/с,  4 — 15000 м/с

Рис. 2 — Зависимость профиля линии H_α от скорости движения, для сравнения приведен профиль этой же линии в спектре Alpha Mon, по вертикали даны значения коэффициента поглощения или относительный поток в нормированном спектре

 

Далее задача сводится к тому, чтобы подбором концентрации газа и скорости движения газовых масс добиться наилучшего совпадения расчетного и наблюденного профиля линии. Следует учесть, что правый край линии наблюденного спектра искажен, поэтому необходимо добиваться совпадения левого края линии и ее центра с расчетом.

Для анализа были взяты спектры, полученные группой Х. Брунтта, размещенные в базе данных Центра астрономических данных в Страсбурге. [6] На рисунке 3 показаны результаты расчета в сравнении с реальным спектром, видно хорошее совпадение указанного участка ядра линии. Расчетные параметры приведены в таблице 1. Температура звезд бралась из данных группы Х. Брунтта.

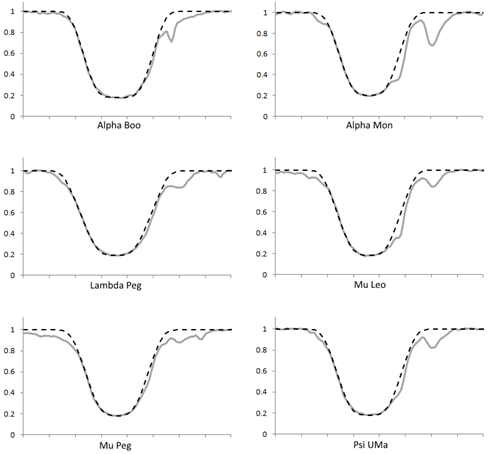
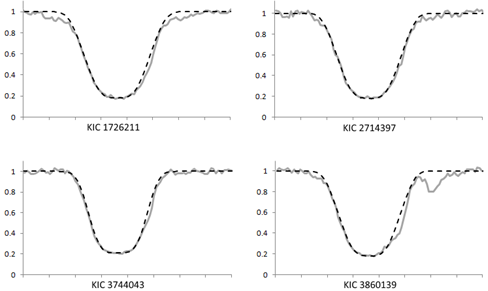
Рис. 3 — Расчетные (пунктир) и наблюденные (серая сплошная линия) профили линий H_α красных гигантов

Таблица 1 — Концентрации и абсолютные

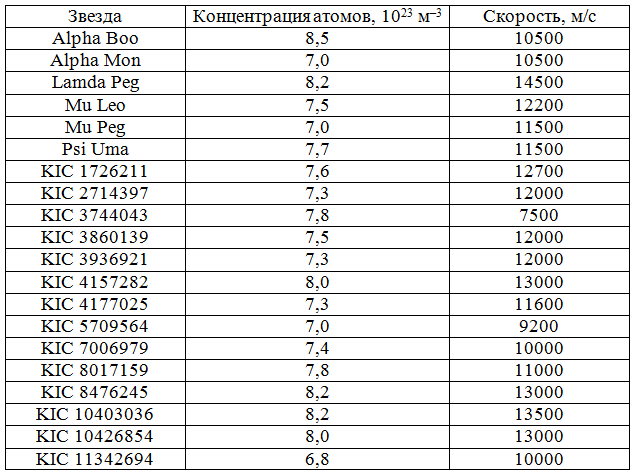
Видно, что абсолютные пространственные скорости движения газа значительно превосходят значения скоростей макротурбуленции, определенные группой Х. Брунтта и Д. Ф. Греем, но лежат внизу пространства значений для сверхгигантов, определенных Т. С. Галкиной. Вопрос о погрешности определения концентрации и скорости движения газовых масс описанным методом остается открытым. Зависимость скорости от температуры не просматривается, но есть некоторая ее зависимость от концентрации.

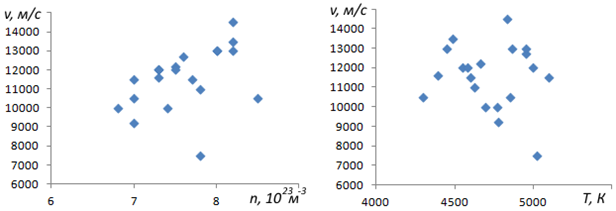
Рис. 4 — Зависимости скорости движения газовых масс от концентрации (слева) и температуры (справа)

 

Причины для высоких скоростей движения газовых масс может быть две: с одной стороны должна иметь место конвекция, с другой стороны быстро вращающееся ядро должно передавать момент окружающему его газу оболочки, при этом обязательно возникнет широтное перемешивание. Данным методом не предусмотрено отделение вращательной скорости оболочки от собственно конвекции и широтного перемешивания. Однозначный набор значений концентрации и скорости, при которых расчетный профиль совпадает с неискаженной частью реального профиля, можно считать критерием достоверности данного метода.

Литература

1. Галкина Т. С. Количественный анализ атмосфер горячих сверхгигантов / Т. С. Галкина, И. М. Копылов. // Известия Крымской астрофизической обсерватории. — 1962. — Т. 28. — С. 35–93.
2. Gray D. F. Rotation and turbulence in G giant stars // The Astrophysical Journal. — 1981. — Vol. 251(1). — Р. 155–161.
3. Gray D. F. The temperature dependence of rotation and turbulence in giant stars // The Astrophysical Journal. — 1982. — Vol. 262(1). — P. 682–699.
4. Brun A. S. Numerical simulations of a rotating red giant star. I. Three-dimensional models of Turbulent convection and associated mean flows / A. S. Brun, A. Palacios // The Astrophysical Journal. — 2009. — Vol. 702. — P. 1078–1097.
5. Bruntt H. Atmospheric parameters of red giants in the Kepler field / H. Bruntt, S. Frandsen, A. O. Thygesen // Astronomy and Astrophysics. — 2011. — Vol. 528. — A 121.
6. Normalized spectra of 20 red giants (Bruntt,+, 2011) // (Engl.) – URL: http://cdsarc.u-strasbg.fr/viz-bin/Cat?J/A+A/528/A121 [22 July 2016].

References

1. Galkina T. S. Quantitative analysis of the atmospheres of hot supergiants / T. S. Galkina, I. M. Kopylov // Izvestiya of the Crimean astrophysical Observatory. — 1962. — Vol. 28. — P. 35–93.
2. Gray D. F. Rotation and turbulence in G giant stars // The Astrophysical Journal. — 1981. — Vol. 251(1). — Р. 155–161.
3. Gray D. F. The temperature dependence of rotation and turbulence in giant stars // The Astrophysical Journal. — 1982. — Vol. 262(1). — P. 682–699.
4. Brun A. S. Numerical simulations of a rotating red giant star. I. Three-dimensional models of Turbulent convection and associated mean flows / A. S. Brun, A. Palacios // The Astrophysical Journal. — 2009. — Vol. 702. — P. 1078–1097.
5. Bruntt H. Atmospheric parameters of red giants in the Kepler field / H. Bruntt, S. Frandsen, A. O. Thygesen // Astronomy and Astrophysics. — 2011. — Vol. 528. — A 121.
6. Normalized spectra of 20 red giants (Bruntt,+, 2011) // (Engl.) – URL: http://cdsarc.u-strasbg.fr/viz-bin/Cat?J/A+A/528/A121 [22 July 2016].