HARMONIC (MATHEMATICAL) AND DISPLACEMENT (PHYSICAL) PHASE
Рождественский А.Е., Рождественский С.А.
ООО «Физико-техническая корпорация НРС»
ГАРМОНИЧЕСКАЯ (МАТЕМАТИЧЕСКАЯ) И СДВИГОВАЯ (ФИЗИЧЕСКАЯ) ФАЗА
Аннотация
Математичесски сдвиг фаз определяется как часть аргумента между функциями вида sin, cos, c одинаковой частотой-это фаза «гармоническая». В природе сдвиги между феноменами, имеющие малые различия, математически характеризуются множеством гармонических сдвигов фаз. Показано, что сдвиг (смещение) большой системы можно описать одним числом как «сдвиговой фазой» в рамках физического представления о работе обобщенных сил по обобщенным перемещениям.
Ключевые слова: фаза математическая, гармоническая сдвиговая, физическая , сравнение феноменов.Roshdestvensky A.E., Roshdestvensky S.A.
Physic Tehnical Corporation NRS
HARMONIC (MATHEMATICAL) AND DISPLACEMENT (PHYSICAL) PHASE
Abstract
Mathematic ( harmonic) phase concerns argument in functions (sin ), (cos) with the same frequency. For common description any differences between physics phenomenon are suggested the Displacement (shift) phase ore Physical phase. Shift phase is non size energy due common forces with common displacements. Physical phase as idea are responsible for geometrical displacement of any phenomena and for its non size shift energy at the same time.
Keywords: «Mathematic» (ore harmonic) phase, Displacement» phase, common forces and common displacements.Введение.
В работе дано определение понятия "сдвиговой фазы", необходимость которого возникла исходя из физических и геофизических задач и приложений. По форме эта фаза -"интегральная", по сущности -"сдвиговая", т.к. отражает «непохожесть» объектов, измененных или деформированных путем сдвига. В этом смысле сдвиговая фаза есть фаза фаза «физическая», т.к сдвиг можно определить без ограничения общности как нормированную работу обобщенных сил по обобщенным перемещениям.
Сравнение двух феноменов с помощью бесконечного набора гармонических фаз ( спектр любой ограниченной функции бесконечен) возможно, но мало информативно как бесконечный ряд фаз для отдельных гармоник. Слово "интегральная" указывает, что такая фаза определяется в целом, "интегрально" для процесса, явления, без математического разложения на гармоники. Сдвиговая или "физическая" фаза отражает сущность названия, т. по форме упомянутая "физическая" фаза аналогична «сдвигу» объекта как целого, и сводится к гармонической (математической) фазе, если сравниваемые функции (феномены) гармонические. Существенно, что сдвиговая «физическая» фаза с точностью до размерной константы отвечает за процессы трансформации и передачи энергии, т.к. эти процессы, могут быть выражены в форме «сдвиговой фазы», которая тождественно удовлетворяет принципу минимума производства энтропии в изучаемой системе ( условию Эйлера как необходимому условию ), и с точностью до размерной константы количественно определяет физические процессы переноса, сдвигов, изменения плотности источников в сравниваемых полях.
Понятие сдвиговой, интегральной (физической) фазы было введено и использовано в работах научной школы чл -корр. АН СССР Лаппо С.С. его сотрудником А.Е. Рождественским [1,2]. Эти публикации касались анализа переноса механической, лучистой, тепловой энергии в сплошных средах, в геофизической системе океан - атмосфера-земля .
"Метод сдвиговой фазы" дает количественную оценку различиям как собственно математическим объектам , так и физическим процессам и явлениям (определение позиции или положения объекта, «узнавание объекта, нахождение потоков энергии, массы, импульса в материальной среде). Метод сдвиговой фазы также предназначен для вычисления (нахождения) фазы произвольного объекта (или же его положения), явления , сигнала, без применения гармонического (Фурье) анализа. Сдвиговая фаза дает величину временного или пространственного сдвига, а также количественные характеристики в виде потоков энергии, массы импульса для "распределенных объектов", таких как распределенные среды и большие системы.
С одной стороны "фаза" в нашем определении есть кинематическое понятие, -сдвиг или (или интегральная) фаза как параметр различия между формами, фигурами, поверхностями (функциями). С другой стороны выражение для сдвиговой фазы пропорционально процессам переноса (массы, энергии, импульса) в материальной сплошной среде или в большой системе. Практические следствия этого совпадения форм обсуждаются ниже.
Фаза – сравнительный параметр «большой системы». Заметим, что «фаза» как параметр и число, применимо для сравнительного описания множества точек – системы, либо для описания движения одной точки как совокупности ее положений (траектории). Таким образом, одно число (фаза) описывает особенности системы в целом ( распределение свойств, положение точек), или даже "большой" системы, где число элементов велико, и описывает сдвиг или смещение. Смещение есть понятие относительное (сравнительное). Фаза тоже есть «параметр сравнения», имеющий положительный или отрицательный знак в зависимости от направления сдвига в выбранных координатах. 1. Определение - «Сдвиговая» фаза».Введем определение сдвиговой (физической) фазы. Какие есть основания, чтобы назвать фазу «физической». Ниже будет представлено кинематическое и динамическое обоснование. Фаза, которую мы назовем "физической" фазой, определяется для объекта числом, кинематически представляет собой «сдвиг», и ответственна за физические процессы переноса передачи энергии.
О п р е д е л е н и е
Физической (сдвиговой, интегральной, активационной) фазой φ между двумя функциями f1 и f2 будем называть интеграл вида -
, (1)
где C = Const- размерная и нормирующая константа, Ω - область определения фазы. Исходя из (1) пространственный фазовый сдвиг между f1 и f2 равен :
, (2)
где d - элемент площади на области 
(Х), а знак фазы соответствует знаку скалярного произведения.
Соответственно временная фаза равна:
(3)
где Т – отрезок времени
Данное определение фазы совпадает с классическим, если функции f1, f2 являются гармоническими функциями.
Пусть f1 = A1 Sin ( ω х ) , f2 = A2 Sin ( ω х + τ ) , Т -период
Подставляя значения f1, f2 в интеграл (2) имеем -
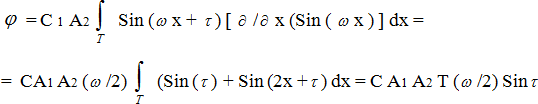
Выбираем константу в виде C = (2 / A1 A2 ω Т), откуда получаем –
φ = Sin τ, откуда при 
Определение физической фазы позволяет дать кинематическую интерпретацию как количественный параметр различия между объектами или финитными функциями в виде «сдвига».
Положим, что одна финитная функция отличается от другой сдвигом т.е.
f 2 (х) = f1(х + τ), рис. 1.Без ограничения общности положим, что функция f1 финитна и вне области [A,B1] равна нулю.
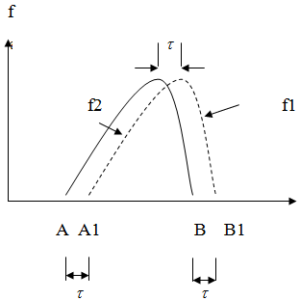
Рис. 1
Вычислим сдвиговую (физическую) фазу между «конгруэнтными» финитными функциями f1 , f2 в соответствии с определением
(3)
Функцию f2 представим в виде степенного ряда по степеням τ,
(4)
Подставляя значение f2 в виде ряда (4) в интеграл вида (3), имеем при малых τ -
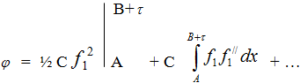(5)
Заметим, что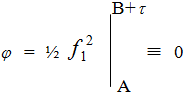 
, откуда при малых сдвигах
(6)
Сдвиговая фаза вида (6) была использована в [2] в исследовании большой геофизической системы океан-атмосфера с нахождением новых природных феноменов, потоков энергии. Интеграл типа (1-3 ) в данном примере дает фазу как «чистый сдвиг» между произвольными финитными функциями при достаточно малом значении этого сдвига.
Вернемся к примеру на рис. 1, и рассмотрим финитную функцию f1, которая симметрична на отрезке А,В, и фазу между f1 и сдвинутой на (τ) функцией f2, см. рис. 2.
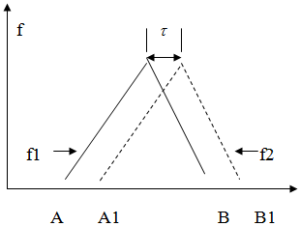
Рис. 2
В случае симметричной на отрезке А,В функции ( f1 ) выражение для фазы вида (5) принимает вид:
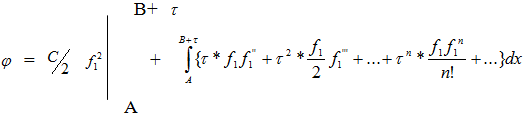(7)
В этом ряду первое слагаемое тождественно равно нулю для любой финитной функции, т.к. 
. В разложении вида (7) все члены ряда с четными степенями также обращаются в нуль при интегрировании, как интегралы от нечетной на отрезке функции. Для четной (симметричной на отрезке (А,В) ) функции имеем из (7):
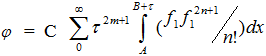(8)
Таким образом, в нашем определении фаза, согласно (8), всегда имеет знак сдвига (τ), т.е. всегда показывает направление сдвига.
Если мы повторим рассуждение о сдвиге и фазе на отрезке сдвига для ассиметричной функции на отрезе, т.е если f1 в (5) будет несимметричной на (А,В), то в ряду типа (5,7) все интегралы вида
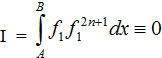, как интегралы от антисимметричной функции на отрезке. Любую функцию на отрезке можно представить в виде суммы симметричной и несимметричной функции. Поэтому для произвольной финитной функции f сдвиг фаз между f (х) и f (х + τ) всегда будет иметь вид ряда (7,8) по нечетным степеням τ и при малых 
.
Таким образом, фазовый сдвиг между финитными функциями в смысле введенного определения, в предельных случаях имеет вид и «чистой фазы φ» (гармонические функции), равной «чистому сдвигу τ» (малые сдвиги).
Единственным ограничением, которое использовалось выше для вывода равенства (6), заключалось в том, чтобы сравниваемые функции в концах отрезка, на котором вычисляется фазовый сдвиг, были равны одной и той же величине, т.е финитны с точностью до константы. В практике вычисления фазовых сдвигов для разных физических процессов, эти величины (значения функции на концах отрезка , как рядов наблюдений) могут иметь разные произвольные значения, например f1 (А) = f1 (В) + С. Тогда в тех же предположениях f1 (х) = f2 (х + ) будем иметь
(9)
Первый член в (9) представляет «чистый» сдвиг, а второй – «чистый» наклон -тангенс угла наклона на отрезке. Мы видим, что физическая фаза есть направленный параметр различия между формами, фигурами, поверхностями ( функциями), который совпадает в предельных случаях с понятием кинематического сдвига и (или) с понятием математической фазы при малом различии f1,f2 и при f(B) = F(A) в (9).
3. Сдвиговая ( физическая) фаза и коэффициент «корреляции».
На первый взгляд интеграл в определении сдвиговой (физической) фазы между двумя функциями f1, f2 (т.е интеграл вида 
) похож на интеграл для определения коэффициента корреляции между ними. Оговоримся, что сходство это отдаленное - фаза имеет знак, коэффициент корреляции знака не имеет.
Сравним понятие физической фазы между функциями f1, f2 с понятием коэффициента корреляции между ними на одном и том же отрезке при условии «чистого сдвига», т.е при условии 
. Оговоримся, что мы не рассматриваем принятые понятия корреляционной и функциональной связей. Существует бесконечное количество математических выражений для тех или иных коэффициентов корреляции – в зависимости от поставленной задачи. Оговоримся, что здесь под коэффициентом корреляции мы будем понимать выражение типа 
Коэффициент корреляции между f1, f2 как функция τ на отрезке (А, В+τ) в принятых обозначениях равен ( см. рис. 1,2 ) –
(10)
В выражении (10) все члены с нечетными степенями будут равны нулю , как интегралы вида R = R ( 
) от антисимметричных на отрезке функций. В итоге мы получаем, что для функций f1, f2, отличающихся на отрезке только сдвигом, коэффициент корреляции представим рядом по четным степеням сдвига, а фазовый сдвиг в смысле принятого определения – рядом по нечетным степеням сдвига, т.е.-
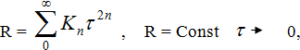(11)
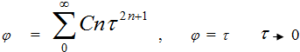
При малых сдвигах τ фазовый сдвиг между финитными функциями равен самой величине сдвига τ, а коэффициент корреляции малые сдвиги τ не «чувствует», и направление сдвига коэффициент корреляции не «замечает». Из (11) следует приближенное выражение при малых τ -
(12)
В кинематическом сдвиге форм (функций), коэффициент корреляции дает степень «сходства», «похожести» форм , а физическая фаза есть степень их «непохожести». Поскольку коэффициент корреляции не зависит от направления сдвига (от знака (φ), поэтому зависимость R(φ) квадратична в (12).
Выводы. Сдвиговая фаза существенно информативна для определения сдвига «по фазе» большой системы как целого объекта относительно прежнего или иного положения во времени или в пространстве. Понятие сдвиговой (физической) фазы позволяет оценивать изменения в больших системах с точки зрения их смещений и деформации (формы, координаты, время) по экспериментальным данным. Это понятие было содержательно использовано в экспериментальной физике [3], в том числе в климатической системе для нахождения крупномасштабных потоков тепла [1,2].
Литература
- Гулев С.К., Лаппо С.С., Рождественский А.Е. Крупномасштабное взаимодействия в системе океан-атмосфера и энергоактивные зоны мирового океана. Л. Гидрометеоиздат, 1990, с. 60-83, 298-306.
- Малышев Г.А. Крупномасштабный теплоперенос в атмосфере над океанами. Автореферат диссертации на соискание ученой степени к.ф.м.н., Москва. ГОИН, 1992, 23 с.
- Рождественский А.Е. Информация как результат формального взаимодействия. Материалы конф. «Физика фундаментальных взаимодействий» Секции ядерной физики отделения общей физики РАН. М. ИТЭФ.2007.
References
- Gulev S.K., Lappo S.S., Rozhdestvenskij A.E. Krupnomasshtabnoe vzaimodejstvija v sisteme okean-atmosfera i jenergoaktivnye zony mirovogo okeana. L. Gidrometeoizdat, 1990, s. 60-83, 298-306.
- Malyshev G.A. Krupnomasshtabnyj teploperenos v atmosfere nad okeanami. Avtoreferat dissertacii na soiskanie uchenoj stepeni k.f.m.n., Moskva. GOIN, 1992, 23 s.
- Rozhdestvenskij A.E. Informacija kak rezul'tat formal'nogo vzaimodejstvija. Materialy konf. «Fizika fundamental'nyh vzaimodejstvij» Sekcii jadernoj fiziki otdelenija obshhej fiziki RAN. M. ITJeF.2007.