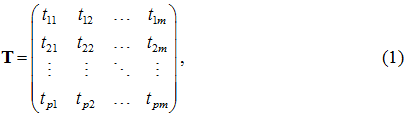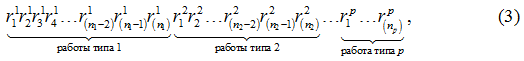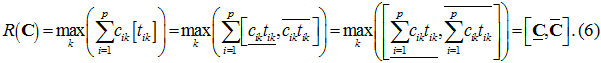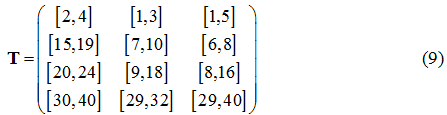SCHEDULING WITH ROUGH DATA USING GENETIC ALGORITHM FOR A GRID COMPUTING

Пархоменко С.С.¹, Леденёва Т.М.²

¹Аспирант, ²Доктор технических наук, Воронежский государственный университет

СОСТАВЛЕНИЕ РАСПИСАНИЯ ДЛЯ РАСПРЕДЕЛЁННЫХ ВЫЧИСЛИТЕЛЬНЫХ СЕТЕЙ В УСЛОВИЯХ НЕТОЧНЫХ ДАННЫХ

Аннотация

В статье предлагаются альтернативные подходы для решения NP-полной задачи распределения работ по исполнителям на основе генетических алгоритмов в условиях неточных исходных данных.

Ключевые слова: генетические алгоритмы, неточные величины.

Parkhomenko S.S.¹, Ledeneva T.M.²

¹Postgraduate student, ²PhD in Engineering, Voronezh State University

SCHEDULING WITH ROUGH DATA USING GENETIC ALGORITHM FOR A GRID COMPUTING

Abstract

The article demonstrates a solving a NP-hard scheduling problem using the genetic algorithm adapted for rough values.

Keywords: genetic algorithm, rough values.

1. Введение

Распределённые вычислительные сети (РВС) являются одним из популярных направлений развития информационных технологий. Замечено, что чем слабее связь между компонентами системы, тем проще аккумулировать вычислительные ресурсы, но сложнее поддерживать высокий уровень эффективности их использования. Основными способами оптимизации работы РВС является сокращение издержек передачи данных и оптимальное распределение нагрузки. Слияние работ в более крупную независимую единицу является одним из способов решения обоих проблем, при этом становится возможным сведения процесса распределение нагрузки к одной из задач теории расписания.

В широком смысле на время работы независимой единицы могут влиять обрабатываемые ей данные. Если принять, что это влияние сложно оценить, то из-за неопределённости в исходных данных становится невозможным прямое использование классических методов составления расписаний.

С популяризацией мягких вычислений одним из направлений современных исследований является разработка методов составления расписаний в условиях неопределённости. Планирование в рамках случайных величин подробно рассмотрено в‍ [1]. В‍ [2] показано применение комбинации нейронных сетей с генетическими алгоритмами для решении различных задач со случайными, нечёткими и неточными данными в условии.

Представив процесс распределения нагрузки для минимизации времени обработки независимых единиц в РВС как задачу распределения работ по исполнителям, работающих параллельно, и допустив, что

• производительность исполнителей различна,
• каждая работа неделима и независима,
• процесс выполнения работы непрерывен,
• в некоторый момент времени исполнитель может выполнять только одну работу,
• работа не требует предварительных операций,
• идентичные работы группируются по типам работ

можно наглядно продемонстрировать специфику решения задач с неопределенностью.

2. Постановка задачи

Пусть дано‍ m исполнителей, обладающих разной производительностью, и‍  работ, сгруппированных в‍ p типов. Каждый исполнитель‍ k∈{1,…,m} может выполнить любую работу, но для выполнения работы‍ i-го типа исполнители могут затрачивать разное время. Этот факт учитывается технологической матрицей

где‍ t_ik‍ – время выполнения работы типа‍ i исполнителем‍ k. Необходимо распределить‍ n работ по‍ m исполнителям (составить план работ) так, чтобы общее время выполнения работ, отсчитывая с начала загрузки хотя бы одного исполнителя и заканчивая по факту освобождения всех исполнителей, было минимальным. В соответствии с нотацией, описанной в‍ [1], сформулированную задачу обозначим в виде‍ R_m||C_max.

В классическом случае, где‍ t_ik∈R, задачу можно свести к задаче дискретного программирования следующего вида

где‍ c_ik ‍ – количество назначенных работ типа‍ i для исполнителя‍ k, n_i‍ – общее (суммарное) количество работ типа‍ i. Совокупность ограничений в‍ (2) гарантирует, что все работы будут задействованы в расписании. Решение задачи‍ (2) представляется в виде матрицы‍ C={c_ik}_pₓm

3. Общая схема генетических алгоритмов

Задача‍ (2) относится к задачам дискретной оптимизации и является NP-полной‍ [1], из чего следует, что универсального алгоритма, отличного от полного перебора, не существует. Общий подход к решению данной задачи может быть основан на нахождении субоптимального решения, что позволит экономить вычислительные ресурсы. Для этого целесообразно использовать генетические алгоритмы (ГА)‍ – метод эвристического поиска решения задач оптимизации, основанный на имитации различных механизмов естественного отбора. Идея алгоритма заключается в манипулировании имеющейся совокупностью закодированных решений (хромосом) с помощью ряда генетических операторов и получении новых хромосом, являющихся новыми вариантами решения‍ [3]. В отличие от случайного поиска, ГА использует информацию, накопленную в процессе эволюции (поиска) от предыдущих поколений. ГА не накладывают ограничений на вид целевой функции и область определения задачи, однако параметры работы часто подбираются эмпирически‍ [4].

Реализация ГА обычно начинается с поиска способа кодирования хромосомы‍ – однозначного представления варианта решения оптимизационной задачи. Каждая хромосома состоит из набора генов.

Общая схема генетического алгоритма включает следующие этапы‍ [5]:

• Инициализация алгоритма. Этап включает кодирование генов и хромосом, определение функции приспособленности, определение условия завершения, выбор начальной популяции.
• Оценка степени приспособленности хромосом в популяции. Осуществляется на основе функции приспособленности, которая строится с учётом целевой функции задачи.
• Проверка условия завершения поиска. В случае выполнения условия, выбор оптимальной хромосомы в качестве решения, иначе‍ – переход к следующему шагу.
• Селекция хромосом. Селекция считается эффективной, если она создаёт возможность перехода из одной подобласти поиска решений в другую. Выделяют два основных типа селекции: случайный выбор и выбор на основе значений целевой функции (например, элитная селекция или селекция на основе заданной шкалы).
• Выполнение генетических операторов. Основными операторами являются: кроссинговер и мутация.
• Создание и оценка новой популяции. Возврат к шагу‍ 2.

Оператор кроссинговера (скрещивания)‍ – конструкция ГА, отвечающая за создание потомков из хромосом родителей. Существует большое количество разновидностей оператора скрещивания‍ [6-7].

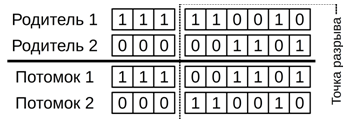
Простейший одноточечный оператор кроссинговера, подразумевает наличие разрезающей обе родительские структуры на два сегмента точки, для последующего склеивания соответствующих сегментов различных родителей и формирования двух новых хромосом потомков. Точка разрыва обычно выбирается случайно. Например:

Рис. 1 - Пример работы одноточечного кроссинговера.

При увеличении точек разрыва увеличивается количество способов обмена участками хромосом между особями, но если точек становится слишком много, нарушается производство приспособленного потомства‍ [6].

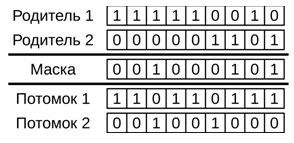
Если гены хромосомы содержат бинарную информацию, то допускается использование универсального оператора кроссинговера. Вместо использования разрезающей точки (точек), используется бинарная маска, которая либо задаётся заранее, либо генерируется случайным образом. Её длина равна длине хромосомы. Потомки выводятся путём сложения по модулю‍ 2 родителей с маской‍ [6]. На рис. 2 представлен пример универсального кроссинговера.

Рис. 2 - Пример работы универсального кроссинговера.

Оператор мутации‍ – конструкция ГА, отвечающая за создание потомка из хромосомы родителя или её части. Существует масса операторов мутации. Например, при одноточечной мутации случайно выбирается ген в родительской хромосоме, который меняется местами с соседним геном, получая хромосому потомка. Популярным способом мутации является полное замещение родительской хромосомы случайно сгенерированной хромосомой потомка‍ [6].

ГА может включать дополнительные операторы. Наиболее распространенные‍ – оператор редукции, нацеленный на сокращение популяции вместе с исключением неудачных решений, и оператор рекомбинации, определяющий процессы, связанные со сменой поколений (итерации работы ГА) и другие‍ [6].

4. Решение дискретной задачи планирования

Пусть для‍ R_m||C_max за каждой задачей закреплён свой ген, значение которого отвечает за номер исполнителя. Сформировав и объединив цепи из работ одного типа, получим представление расписания в виде хромосомы

где‍ r_jⁱ∈[1,m] ‍ – локус хромосомы‍ – номер исполнителя для‍ j-ой работы‍ i-го типа. Очевидно, что длина хромосомы‍ .

Для оценки особей популяции (их хромосом) используется целевая функции задачи‍ (2).

Отбор (селекцию) будет производиться следующим образом: популяция выстраивается в линейный список и каждая особь на нечётной позиции скрещивается с соседом, стоящим впереди. Такой отбор позволяет реализовать частично параллельную версию ГА, например, с применением технологии OpenMP, при этом гарантируя участие всех особей без дополнительных механизмов контроля за использованием хромосомы в вычислениях (синхронизации). Включение в параллельную секцию оценки особей, селекции, операторов кроссинговера и мутации позволяет существенно ускорить поиск субоптимального решения.

В качестве оператора скрещивания используется модифицированный одноточечный кроссинговер. Первая модификация включает в себя запрет на скрещивание между родственниками. Под родственниками будем понимать особей, представляющие одинаковое решение с помощью различных хромосом. Пусть, например, имеются следующие особи:

В данном случае видно, что две хромосомы представляют одинаковое решение. Так, например, в обоих случаях для работы типа 1 c₁₁=8, c₁₂=2, c₁₃=1, c₁₄=0. Аналогичная ситуация с работой типа 2: c₂₁=4, c₂₂=5, c₂₃=2, c₂₄=1. Очевидно, что значение целевой функции тоже будет одинаковым. Для уничтожения дубликата решения (родственника) перед скрещиванием одна из родительских особей замещается новой, со случайно сгенерированной хромосомой, после чего выполняется одноточечный кроссинговер.

Вторая модификация заключается в локальном применении селекции. Вычислим значения целевых оптимизационных функций потомков и родителей. Из четвёрки особей места родителей займут те, у кого значения целевой функции меньше, чем у остальных.

Поскольку для селекции популяция выстроена в линейный список, то для того чтобы особь имела возможность скрещиваться с другими членами популяции, необходим дополнительный оператор перемешивания популяции, при этом некоторые особи подвергаются случайной мутации.

Время работы генетического алгоритма будет ограничено числом итераций.

5. Задача составления расписания в условиях неточных данных

Предположим, что исходная информация для задачи‍ R_m||C_max является приближенной и выражается в виде интервальных чисел, которые относятся к классу неточных величин. Они являются самым общим способом представления неопределённой информации о времени выполнения работ.

Согласно‍ [8] под интервальным числом‍ [a] будем понимать вещественный отрезок‍ , где‍ . Распространёнными характеристиками интервального числа являются ширина числа‍  и его медиана‍ . При‍ ‍ получим обычное число‍ [8].

Пусть исходные данные представлены в виде интервальной технологической матрицы‍ ‍ – матрицы, компоненты которой представляют собой интервальные значения времени выполнения работ. Для решения задачи планирования на основе ГА, предлагаются следующие подходы, позволяющие получить субоптимальный план.

Сведение задачи к её дискретному варианту подразумевает, что в широком смысле‍  можно получить с помощью вычисления‍ α ∈[0,1] значений элементов по формуле‍ [2]

При различных‍ ‍ получим следующие варианты планирования:

• α→1, пессимистичное планирование (оптимизация по максимальному времени выполнения работ);
• α→0, оптимистичное планирование;
• α→0,5, в результате чего‍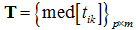 , планирование по центральным величинам;
• α~α_ik, в результате чего формируется отдельная матрица‍ , по которой каждому элементу‍ [t_ik] ставится в соответствие свой коэффициент‍ α_ik для преобразования‍ .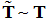

Матрица‍  может быть сформирована лицом, принимающим решения (экспертом), а следовательно можно говорить об использовании экспертной информации. Однако знаний эксперта может не хватить для тонкой и точной подстройки коэффициентов, из-за чего решения будут неоптимальными. Автоматизировать настройку матрицы‍ A можно с помощью механизма обратной связи, но здесь возникают следующие проблемы:

• проблема обучения‍ – очевидно, что сразу оптимальные коэффициенты‍ α_ik получить не удастся, следовательно их подбор превращается в отдельный итерационный процесс, причём с учётом изменений условия задачи‍ R_m||C_max; кроме того, требуется активное выполнение пробных действий, явным образом организованный поиск методом проб и ошибок;
• проблема оценки‍ – сложно определить, насколько текущее значение‍ α_ik лучше или хуже другого; проблема усугубляется тем, что‍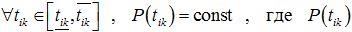 , где‍ ‍ – вероятность появления значения‍ t_ik, из чего следует потеря оптимальности матрицы‍ A при изменении условий выполнения работ.

Независимо от выбора‍ α неопределённость об времени выполнения работы «ликвидируется» ещё до входа в ГА, в результате чего он оперирует уже вещественными числами.

Другой способ основывается на том, что решением задачи‍ (2), в конечном итоге, является хромосома-победитель, выявленная из всей популяции с помощью функции приспособленности. Однако ранжировать хромосомы при наличии неопределённости в ней можно различными способами. Пусть ГА оперирует непосредственно интервальными числами. В силу простоты функции приспособленности достаточно опираться на интервальную арифметику‍ [8].

Пусть функция приспособленности для хромосомы-решения‍ C, содержащая неопределённость имеет вид (учитывая‍ c_ik≥0)

Для реализации оператора‍  используется распространённый способ сравнения интервальных чисел

зачастую при‍ α=0.5‍[8-9]. Однако конкретно для задачи‍ (2) допусти́м вариант

Согласно‍ (8) при сравнении планов вводится приоритет: сначала анализируется наихудший возможный случай выполнения работ по плану, затем, если последствия одинаковы, просматривается наилучший случай.

6. Вычислительный эксперимент

Для реализации вычислительного эксперимента разработана компьютерная программа на языке‍ C с применением технологии параллельного программирования OpenMP. Целью вычислительного эксперимента заключается в анализе влияния способа сравнения хромосом на конечное расписание. Сравним стандартный способ‍ (7) при‍ α=0.5‍ и способ на основе приоритета‍ (8).

Пусть имеется‍ m=3 исполнителя и‍ n=500 работ, сгруппированных в‍ p=4 типов: n₁=180, n₂=80, n₃=140, n₄=100. Зададим технологическую матрицу:

Случайным образом сгенерировав начальную популяцию из‍ 10000 особей, ГА выполнил‍ 35000 итераций. При переходе от одной итерации к другой случайным образом мутировали 32 особи. В результате были получены следующие субоптимальные решения:

где‍ C₁‍ – решение составленное с применением стандартного сравнения, а‍ C₂‍ – приоритетного.

В ходе экспериментов замечено, что с каждой итерацией увеличивается потребность в уничтожении дубликатов решения для поддержания разнообразия внутри популяции.

Сравним два полученных плана. Отметим, что . Видно, что при распределении работ по плану‍ C₂‍, построенному с применением приоритетного сравнения, снижаются максимально возможные временные затраты, а также формируется расписания с более чёткими границами по времени, что следует из‍ .

Появление неопределённости в условии задач часто требует пересмотра методов их решения. В контексте задачи планирования РВС, наличие неопределённости выступает в качестве допущения, упрощающего сбор и анализ первичных данных. Так для представления неопределённости в затратах времени были использованы интервальные числа, дающие информацию только о временны́х границах. Благодаря ГА и его модификациям рассмотрен способ составления субоптимального плана, снижающего общую занятость РВС.

Этот способ в сочетании с нейронными сетями позволяет получить гибридный алгоритм, сочетающий эффективность и адаптивность к изменяющимся условиям работы РВС.

Литература

1. Pinedo M. L. Scheduling: theory, algorithms, and systems. – Springer Science & Business Media, 2012.
2. Лю Б. Теория и практика неопределенного программирования / Б. Лю; Пер. с англ. – М.: БИНОМ. Лаборатория знаний, 2014. – 416 с.
3. Панченко Т. В. Символьная модель ГА // Генетические алгоритмы: учебно-методическое пособие. – Астрахань: Издательский дом «Астраханский университет». – С. 41-50.
4. Родькина М. Б. Разработка эволюционных алгоритмов для решения задач теории расписаний в условиях неопределённости: Автореф. дис. канд. техн. каук. – Воронеж, 2013. – 16 с.
5. Пегат А. Самоорганизация и самонастройка нечётких моделей методом поиска // Нечёткое моделирование и управление. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2013. – С. 530-538.
6. Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы. – М.: ФИЗМАТЛИТ, 2006. – 320 с.
7. Каширина И. Л. Введение в эволюционное моделирование. – Воронеж, 2007. – 39 с.
8. Добронец Б. С. Интервальные числа // Интервальная математика: учеб. пособие. – Красноярск: Краснояр. гос. ун-т. – С. 31-33.
9. Левин В. И. Сравнение интервальных чисел и оптимизация систем с интервальными параметрами // Автомат. и телемех. – № 4. – 2004. – С. 133-142.

References

1. Pinedo M. L. Scheduling: theory, algorithms, and systems. – Springer Science & Business Media, 2012.
2. Lju B. Teorija i praktika neopredelennogo programmirovanija / B. Lju; Per. s angl. – M.: BINOM. Laboratorija znanij, 2014. – 416 s.
3. Panchenko T. V. Simvol'naja model' GA // Geneticheskie algoritmy: uchebno-metodicheskoe posobie. – Astrahan': Izdatel'skij dom «Astrahanskij universitet». – S. 41-50.
4. Rod'kina M. B. Razrabotka jevoljucionnyh algoritmov dlja reshenija zadach teorii raspisanij v uslovijah neopredeljonnosti: Avtoref. dis. kand. tehn. kauk. – Voronezh, 2013. – 16 s.
5. Pegat A. Samoorganizacija i samonastrojka nechjotkih modelej metodom poiska // Nechjotkoe modelirovanie i upravlenie. – 2-e izd. – M.: BINOM. Laboratorija znanij, 2013. – S. 530-538.
6. Gladkov L. A., Kurejchik V. V., Kurejchik V. M. Geneticheskie algoritmy. – M.: FIZMATLIT, 2006. – 320 s.
7. Kashirina I. L. Vvedenie v jevoljucionnoe modelirovanie. – Voronezh, 2007. – 39 s.
8. Dobronec B. S. Interval'nye chisla // Interval'naja matematika: ucheb. posobie. – Krasnojarsk: Krasnojar. gos. un-t. – S. 31-33.
9. Levin V. I. Sravnenie interval'nyh chisel i optimizacija sistem s interval'nymi parametrami // Avtomat. i telemeh. – № 4. – 2004. – S. 133-142.