IDEAS AND METHODS OF APPLIED GEOMETRY AND THEIR APPLICATIONS IN ENGINEERING

Нартова Л. Г.¹, Гузненков В.Н.²

¹доктор педагогических наук, профессор, Московский авиационный институт (национальный исследовательский университет МАИ); ²доктор педагогических наук, доцент, Московский государственный технический университет имени Н.Э. Баумана (МГТУ им. Н.Э. Баумана)

ИДЕИ И МЕТОДЫ ПРИКЛАДНОЙ ГЕОМЕТРИИ И ИХ ПРИМЕНЕНИЕ В ТЕХНИКЕ

Аннотация

Рассматриваются начертательная геометрия и прикладная геометрия, как учебные и научные дисциплины. Приведен пример практического использования методов начертательной геометрии и прикладной геометрии при решении задач конструирования технических поверхностей летательных аппаратов.

Ключевые слова: начертательная геометрия, прикладная геометрия, геометрическое моделирование.

Nartova L.G.¹, Guznenkov V.N.²

¹Doctor of Pedagogy, Professor, Moscow Aviation Institute (National Research University), ²Doctor of Pedagogy, Bauman Moscow State Technical University

IDEAS AND METHODS OF APPLIED GEOMETRY AND THEIR APPLICATIONS IN ENGINEERING

Abstract

Considered descriptive geometry and applied geometry, as educational and scientific disciplines. An example of the practical use of methods of descriptive geometry and applied geometry in solving the technical design of aircraft surfaces.

Keywords: descriptive geometry, applied geometry, geometric modeling.

Начертательная геометрия, как учебный предмет и теоретическое обоснование нового геометрического знания, возникла еще в 19 веке [1]. Ее основателем, как моногамной геометрической области знания, считается по праву выдающийся французский геометр, член Национального института в Париже (который соответствовал по своему научному статусу Академии Наук) Гаспар Монж.

В то далекое время все крупные ученые, как правило, обладали большой эрудицией в различных областях научного знания. Это с полным правом можно отнести к весьма разносторонней научной деятельности Г. Монжа. Ему принадлежат серьезные теоретические изыскания в области математического анализа, в установлении тесных связей с высшей геометрией, в том числе и дифференциальной, и серьезные геометрические интерпретации уже известных научных дисциплин.

В классическом понимании, начертательная геометрия представляет собой ветвь высшей геометрии, основанной на широком применении метода проекционных изображений [2]. Именно так и классифицировал ее и сам Гаспар Монж. Однако, с течением времени, она все больше и больше обрастала глубокой общностью рассуждений, свойственной каждой математической науке. Одновременно возрастала и возможность ее поистине универсального применения в исследовании и конструировании объектов различной природы. Начертательная геометрия все больше и больше начинает играть определенную роль и в математике, физике, химии, кристаллографии и даже в педагогике (параметрический метод построения проекций), и в психологии (в проблемах восприятия пространства различного числа измерений), и т.д [3].

Все это дало возможность еще в прошлом веке отметить характерный двойственный характер начертательной геометрии, причислив ее окончательно к числу прикладных наук, и присвоить ей название – прикладная геометрия. Это немаловажное обстоятельство и позволяет ей выживать и эффективно развиваться в столь долгом временном периоде.

В частности об этом всерьез и основательно упоминается в книге Джона Хоргана «Конец науки»: «Прикладная наука будет жить долгое время, т.к. ученые продолжают разработку новых универсальных материалов:

- более быстрых и сложных компьютеров;

- новых и более перспективных генно-инженерных технологий, делающих нас здоровее, сильнее, увеличивающих продолжительность жизни, и опирающихся на современные достижения математики, в том числе и высшей геометрии…».

В этой связи уместно отметить тот факт, что важнейшей особенностью всякого геометрического знания является поистине универсальная возможность его применения. Так еще академик А.Н. Колмогоров писал: « … однако везде, где это возможно, математики стремятся сделать изучаемые ими проблемы геометрически наглядными, поэтому геометрическая интуиция, геометрическое воображение, пространственные представления, геометрические интерпретации играют существенную роль в процессе изучения различных разделов математики, физики и т.д.». Научно-педагогический комментарий самого Г. Монжа: «Если бы мне снова пришлось начать эту работу (речь идет о написании курса начертательной геометрии), я напечатал бы ее в два столбца: в первом поместил бы решения геометрических задач путем вычисления, а во втором – решения тех же задач, но исполненные путем графических построений. Читатели пожалуй были бы очень удивлены, увидев, что второй столбец почти всегда заслуживал бы предпочтения, как по ясности, так и по простоте доказательств».

Принимая во внимание типологию процесса возникновения новых областей знания, прикладную геометрию можно было бы поместить на границу существования двух основных типов развития наук, типа А и типа С. Поясним это более подробно.

Тип А. Процесс возникновения складывается из возможностей и потребностей исследования новых неизвестных прежде или исследовавшихся спорадически предметных областей.

В нашем случае компонентами является область решения технических задач, основанная на геометрических методах и их интерпретациях, применяющихся в начертательной геометрии плюс САПР (имеется ввиду смысловой эквивалент английского CAD, означающий проектирование с помощью ЭВМ).

Иначе в содержательном смысле – это конструирование, возможности автоматизации которого обеспечиваются использованием цифровых вычислительных средств. В настоящее время все это трактуется как компьютерное геометрическое моделирование [4].

Тип С. Непосредственные связи двух или трех традиционных дисциплин приводят к консолидации предметов отдельных наук и к возникновению пограничных дисциплин. В этом случае ведущую роль приобретают те проблемы, которые разрешаются на стыке отдельных областей знания, а следовательно, возникновение новых областей знания происходит не в результате произвола и субъективных склонностей ученых, а представляет объективный процесс. Образование подобного рода пограничных научных дисциплин не меняло в дальнейшем существовании «материнских дисциплин». Но если говорить о состоянии высшей начертательной геометрии в ХХ столетии и сейчас, то следует в первую очередь учитывать влияние прикладных задач в области механики, физики, теории механизмов и машин, САПР и фундаментальных результатов вычислительной геометрии [5]. Все это свидетельствует о новом научно прикладном направлении развития наук, воедино связавшем научные основания начертательной геометрии с современными вычислительными методами в процессе конструирования, что и привело к эволюции классической начертательной геометрии в геометрию прикладную. В этом направлении уместно отметить необычайно плодотворную деятельность кафедры прикладной геометрии МАИ, созданной в 1948 году. Под руководством первого заведующего кафедрой действительного члена АПН СССР, доктора физико-математических наук, заслуженного деятеля науки и техники профессора Н.Ф. Четверухина были получены замечательные результаты как в научной деятельности так и учебной работе. Теоретические изыскания, положенные в основу начертательной геометрии: теория условных изображений, параметрический метод, обобщение принципов параллельной аксонометрии, позволили Н.Ф. Четверухину создать великолепную научную школу, подготовить и выпустить большое количество аспирантов и докторантов – будущих специалистов широкого профиля в области теоретических основ начертательной геометрии, способных внедрить современные теоретические методы ее преподавания на всей территории Советского Союза и за его пределами.

Этот комментарий позволит лучше понять и оценить значение и силу научного творчества коллектива кафедры прикладной геометрии МАИ. Это  дало возможность расширить и углубить круг прикладных задач, решаемых методами начертательной, прикладной геометрии. Ее методы нашли свое блестящее воплощение в CAD/CAM/CAE-системах [6]. Известный специалист в области математического обеспечения CAD/CAM-систем П. Безье отмечал, что создание систем автоматизированного проектирования невозможно без знания геометрии, особенно прикладной геометрии.

Итак, нами отмечено, что прикладная геометрия очень многогранная наука, включающая в себя решение самых сложных геометрических задач разной направленности [7]. В настоящее время решаются задачи геометрического конструирования разных геометрических объектов, в том числе авиационного профиля. Следует отметить, что эти задачи отличаются общностью методов [8], т.к. их решение основано на оптимизации большого количества параметров, входящих в функциональные зависимости, описывающие тот или иной объект, а далее вступают в силу и применяются общие законы автоматизации в их стандартной форме.

Сопоставляя методы начертательной геометрии и номографическое моделирование, можно получить весьма эффективное и изящное решение такой классической задачи как квадратичная интерполяция. С другой стороны, номографические интерпретации плоских кривых, поверхностей приводят к важнейшим понятиям в номографии – понятию криволинейных шкал и сетчатых номограмм, составляющих основу для введения в рассмотрение номограмм более общих классов. Так, например, сетчатые номограммы можно интерпретировать как плоские сечения поверхностей самого общего вида, заданных непрерывными функциями в неявной форме F(x,y,z)=0, а основной метод начертательной геометрии – метод Монжа можно с успехом применить для конструирования плоских эквивалентов сложных пространственных номограмм. Отметим, что в процессе математической обработки эмпирических данных, а это одна из серьезнейших задач конструирования технических поверхностей, в частности, в создании летательных аппаратов разных классов приходится решать задачу об интерполировании функций определенного типа.

Покажем, как это делается. Предположим, что исходная функциональная зависимость задана в виде таблицы, в которой допустима квадратичная интерполяция. В декартовой системе координат (0uv) трем парам значений переменных (u₁v₁), (u₂v₂), (u₃v₃), взятых из этой таблицы, соответствует интерполяционная кривая v = au² + bu + c (1), коэффициенты которой (параметры) определяются из системы уравнений:

v₁ = au₁² + bu₁ + c

                        v₂ = au₂² + bu₂ + c                   (2)

v₃ = au₃² + bu₃ + c

Из условия совместимости уравнения (1) и системы (2) можно получить уравнение интерполяционной кривой в виде:

│u₁    u₁²    v₁   1│

        │u₂    u₂²    v₂   1│ = 0

                   │u₃    u₃²    v₃   1│             (3)

  │u     u      v     1│

Предположим, что заданы определенные интервалы изменений переменных u, v. Тогда уравнение (3) можно интерпретировать пространственной номограммой, взяв в качестве разрешающего индекса определенную плоскость.

Итак, в прямоугольной системе координат 0xyz уравнение (3) определяет проецирующую поверхность, направляющей которой служит парабола, симметричная относительно оси координат.

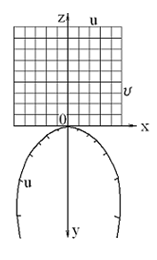
Теперь пространственная номограмма уравнения (3) будет состоять из четырех бинарных полей (u₁,v₁), (u₂,v₂), (u₃,v₃), (u,v), расположенных на этой поверхности. Одно из семейств линий представлено образующими цилиндра (это прямые u₁, u₂, u₃, u), другое линиями пересечения полученной поверхности с плоскостями уровня z = const. Эти линии имеют соответственно пометки v₁, v₂, v₃, v. Геометрически схема пользования номограммой состоит в следующем: в пространстве находим положение разрешающей плоскости ∑, при котором она пройдет через три точки с заданными пометками (u₁,v₁), (u₂,v₂), (u₃,v₃), далее выбираем образующую цилиндра с пометкой «u» и отмечаем точку ее пересечения с плоскостью ∑. Тогда ордината этой точки равна значению ответной переменной v. Теперь спроецируем данную поверхность ортогонально на плоскости П₁, П₂, совпадающие с координатными плоскостями x0y и y0z. Тогда на горизонтальной плоскости получим совпавшую шкалу переменных u₁, u₂, u₃, u, расположенную на параболе, а на фронтальной плоскости – общее ортогональное бинарное поле для переменных (u₁,v₁), (u₂,v₂), (u₃,v₃), (u,v), состоящее из помеченных прямых параллельных оси 0z (рис. 1).

Рис. 1

Рассмотрим второй случай применения чертежа Монжа для получения канонической формы пространственной номограммы определенного типа. Предположим, что дана составная номограмма с прямоугольной немой шкалой и двойным выравниванием, что означает, что ответную переменную на ней можно найти с помощью двух разрешающих прямых.

Итак, пусть немая шкала расположена на оси абсцисс и уравнения четырех шкал записаны в виде:

u = f_i(α_i),

v = φ_i(α_i)

где, i = 1, 2, 3, 4.

Примем плоскости составляющих номограмм за координатные совмещенные плоскости (z, x) (x, y). Тогда для первой номограммы u = x, v = z, для второй номограммы u = x, v = y. Точки M, N, P, Q, дающие решение уравнения и принадлежащие одной разрешающей плоскости, будут иметь в пространстве следующие координаты:

M [x = f₁(α₁), 0, z = φ₁(α₁)]

N [x = f₂(α₂), 0, z = φ₂(α₂)]

P [x = f₃(α₃), y = φ₃(α₃), 0]

Q [x = f₄(α₄), y = φ₄(α₄), 0]

Итак, на эпюре Монжа плоскости элементарных составляющих номограмм совпали с горизонтальной и фронтальной плоскостями эпюра. Заметим, переходя снова в пространство 0xyz, прямые MN и PQ можно считать следами разрешающей плоскости номограммы.

Так как четыре текущие точки M, N, P, Q принадлежат одной разрешающей плоскости, то это условие можно записать в следующей форме:

│ f₁(α₁)  0  φ₁(α₁)  1 │

      │ f₂(α₂)  0  φ₂(α₂)  1 │ = 0

│ f₃(α₃)  φ₃(α₃)  0  1 │

│ f₄(α₄)  φ₄(α₄)  0  1 │

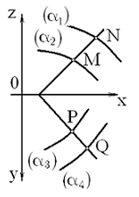
Это уравнение, записанное в форме определителя Соро (французский номограф впервые получивший это выражение) и представляет собой в таком компактном виде каноническую форму уравнения с четырьмя переменными, представленную номограммой рассмотренного вида (рис. 2).

Рис. 2

Литература

1. Гузненков В.Н. Геометро-графическая подготовка в техническом университете // Российский научный журнал. – 2013. – № 6. – С. 159–166.
2. Гузненков В.Н. Тенденция развития геометро-графического образования в техническом университете // Инновации в образовании. – 2014. – № 12. – С. 131–137.
3. Якунин В.И., Гузненков В.Н. Геометро-графические дисциплины в техническом университете // Теория и практика общественного развития. – 2014. – № 17. – С. 191–195.
4. 4. Гузненков В.Н., Демидов С.Г. Autodesk Inventor в курсе инженерной графики. Учебное пособие для вузов. – М.: Горячая линия–Телеком, 2009. – 144 с.
5. Якунин В.И., Гузненков В.Н., Журбенко П.А. Геометрическое моделирование как междисциплинарный язык // Дискуссия. – 2012. – № 12. – С. 161–166.
6. Гузненков В.Н., Журбенко П.А. Autodesk Inventor 2012. Трехмерное моделирование деталей и создание чертежей: учеб. пособие. – М.: ДМК Пресс, 2012. – 120 с.
7. Якунин В.И., Гузненков В.Н. Геометрическое моделирование как обобщение методов прикладной геометрии и ее разделов // Интеграл. – 2012. – № 5. – С. 120–121.
8. Гузненков В.Н., Журбенко П.А. Модель как ключевое понятие геометро-графической подготовки // Alma mater (Вестник высшей школы). – 2013. – № 4. – С. 82–87.

References

1. Guznenkov V.N. Geometro-graficheskaya podgotovka v tekhnicheskom universitete // Rossiyskiy nauchnyy zhurnal. – 2013. – № 6. – S. 159–166.
2. Guznenkov V.N. Tendentsiya razvitiya geometro-graficheskogo obrazovaniya v tekhnicheskom universitete // Innovatsii v obrazovanii. – 2014. – № 12. – S. 131–137.
3. Yakunin V.I., Guznenkov V.N. Geometro-graficheskie distsipliny v tekhnicheskom universitete // Teoriya i praktika obschestvennogo razvitiya. – 2014. – № 17. – S. 191–195.
4. 4. Guznenkov V.N., Demidov S.G. Autodesk Inventor v kurse inzhenernoy grafiki. – М.: Goryachaya liniya–Telecom, 2009. – 144 s.
5. Yakunin V.I., Guznenkov V.N., Zhurbenko P.A. Geometricheskoe modelirovanie kak mezhdistsiplinarnyy yazyk // Diskussiya. – 2012. – № 12. – S. 161–166.
6. Guznenkov V.N., Zhurbenko P.A. Autodesk Inventor 2012. – М.: DМК Press, 2012. – 120 s.
7. Yakunin V.I., Guznenkov V.N. Geometricheskoe modelirovanie kak obobschenie metodov prikladnoy geometrii i ee razdelov // Интеграл. – 2012. – № 5. – S. 120–121.
8. Guznenkov V.N., Zhurbenko P.A. Моdel kak klyuchevoe ponyatie geometro-graficheskoy podgotovki // Alma mater. – 2013. – № 4. – S. 82–87.