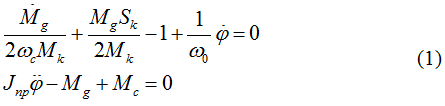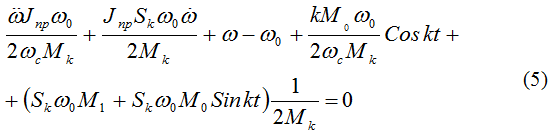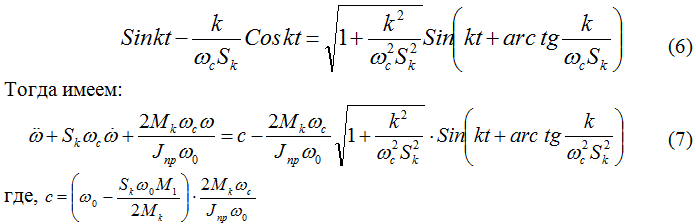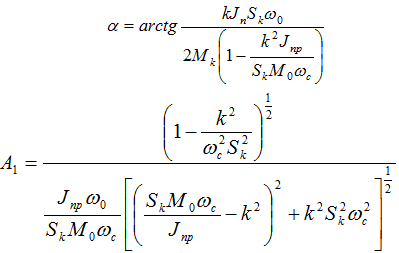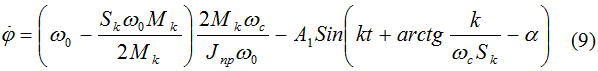ANALYSIS OF DYNAMICS SAW CYLINDER JEAN

Джанпаизова В.М.¹, Юнусов С.М.², Джураев А.³, Торебаев Б.П.⁴, Отарбекова С.Ж.⁵

¹доцент, кандидат химических наук, Южно-Казахстанский государственный университет им. М. Ауэзова, Шымкент, Республика Казахстан;  ²доцент, кандидат технических наук, ³профессор,  доктор технических наук, Ташкентский институт текстильной и легкой промышленности, Ташкент, РУ; ⁴старший преподаватель,  ⁵магистр технических наук, преподаватель, Южно-Казахстанский государственный университет им. М. Ауэзова, Шымкент, Республика Казахстан

АНАЛИЗ ДИНАМИКИ ПИЛЬНОГО ЦИЛИНДРА ДЖИНА

 Аннотация

В статье рассмотрены результаты  исследования по изучению характера движения пильного цилиндра, с целью  определения динамики движения пильного цилиндра. Последовательность проведенных расчетов показало, что на изменение угловой скорости и нагруженности пильного цилиндра джина в основном влияют значение  момента инерции системы. По результатам исследования рекомендованы рациональные значения приведенного момента инерции пильного цилиндра.

Ключевые слова: пильный джин, кинематическая и расчетная схема, машинный агрегат, двигатель, пильный цилиндр, угловая скорость, математическая модель.

Janpaizova V.M.¹, Yunusov S.Z.², Dzhuraev A.³, Torebaev B.P.⁴, Otarbekova S.Zh.⁵

¹assistant professor,  kandidat himicheskih nauk,  M. Auezov South Kazakhstan State University, Shymkent, Kazakhstan; ²assistant professor, kandidat tehnicheskih nauk,   ³professor, doctor of technical sciences, Tashkent Institute of Textile and Light Industry, Tashkent, Uzbekistan; ⁴starshij  prepodavatel,  ⁵master of engineering, prepodavatel,  M. Auezov South Kazakhstan State University, Shymkent, Kazakhstan

 ANALYSIS OF DYNAMICS SAW CYLINDER JEAN

Abstract

The article describes the results of a study on the nature of the motion of the saw cylinder, in order to determine the dynamics of movement of the saw cylinder. The sequence of the calculations showed that a change in the angular velocity of the cylinder and the loading of the saw gin is mainly influenced by the value of the moment of inertia of the system. The study recommended the rational values of the reduced moment of inertia of the saw cylinder.

Keywords: saw gin, kinematic and design scheme, engine assembly, engine cylinder saw, angular velocity, mathematical model,

В пильных джинах главным рабочим органом является пильный цилиндр. Значительная мощность в машине, до 75 кВт потребляет пильный цилиндр. Важными являются исследования по изучению характера движения пильного цилиндра. При этом пильный цилиндр является массивным и влияние на его скоростной режим сопротивления от хлопка-сырца фактически будет не значительным. При этом на характер движения в основном будет влиять изменения момента инерции цилиндра.

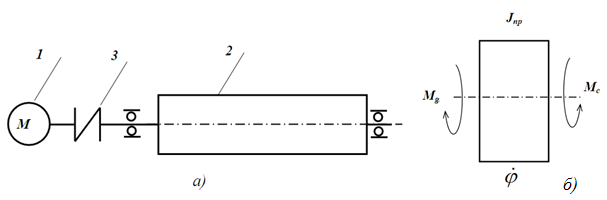
На рис. 1 представлена кинематическая и расчетная схема машинного агрегата с механизмом пильного цилиндра джина. Из них, видно, что ротор двигателя 1 и пильный цилиндр 2 связаны муфтой 3 и лежать на одной оси. Поэтому динамику данной системы желательно рассмотреть как одномассовую (см. рис. 1).

Для данной системы составим математическую модель с помощью известной методике [1]:

где, M_g, M_k-движущий момент двигателя и его критическое значение; φ -угловое перемещение вала пильного цилиндра; ω₀, S_k - угловая частота идеального холостого хода и критическое скольжение, J_пр - приведенный момент инерции ротора двигателя к валу пильного цилиндра; М_с - технологическое сопротивление от джинируемого хлопка-сырца; ω_с -  угловая частота сети.

На основе результатов экспериментальных исследований [2], приблизительно технологическое сопротивление аппроксимируем функцией

где, М₁, М₀ - постоянное и амплитудное составляющие момента сопротивления от хлопка; k - частота изменения сопротивления.

         1-двигатель,        2-пильный цилиндр,    3-муфта

Рис. 1 - Кинематическая (а) и расчетная схема (б) машинного агрегата пильного цилиндра:

Тогда второе уравнение запишем в виде:

Из (3) берем производное по времени:

Учитывая  и подставив в первое уравнение системы (1) полученные значения M_g и  из второго уравнения системы (1) и (4) получим следующее уравнение:

В полученном дифференциальном уравнении (5) второго порядка относительно переменной угловой скорости пильного цилиндра производим следующие преобразования:

Учитывая начальное условия  и используя стандартную методику решения [3], получим общее решение дифференциального уравнения(7):

где,

Полученное решение (8) интегрировав можно вывести выражение для определения углового перемещения пильного цилиндра джина. Но, для оценки динамики движения пильного цилиндра целесообразным является анализ угловой скорости пильного цилиндра. В уравнении (8) первые два слагаемых в основном характеризуют свободные колебания системы и они влияют в переходном режиме пуска машинного агрегата пильного джина. Эти слагаемые с истечением времени стремятся к нулю. Нас интересовало в основном установившиеся режим вращения пильного цилиндра. Тогда решение (5) можно переписать в следующем виде:

Численное решение задачи производили при следующих значениях параметров машинного агрегата:

Номинальная мощность асинхронного электродвигателя, N=75 кВт; номинальное число оборотов ротора электродвигателя, n=735 мин^-1; критический момент на валу двигателя, М_кр=1948,8Нм; номинальный момент, М_н=М_кр/2=974,4 Нм; частота сети f=50 Гц; к.п.д. двигателя η=0,925; номинальный коэффициент мощности двигателя, cosφ=0,85; угловая скорость идеального холостого хода, ω₀=78,54 с^-1; номинальная угловая скорость, ω_н= 76,97 с^-1; номинальные значение скольжения двигателя, S_н=(ω₀-ω_н)/ ω₀= 0,02; критическое скольжение, S_k= 0,075; число пар полюсов, р = 4; суммарный момент инерции масс, приведенные к валу двигателя,

J_пр= 4,25кгм²; среднее значение постоянной составляющей момента сопротивления от хлопка-сырца, М₁= 722,5Нм; коэффициент жесткости, с=23065,2 Нм/рад; коэффициент диссипации муфты, b=128,5 Нмс/рад. [4].

Исследованиями выявлено, что на изменение угловой скорости и нагруженности пильного цилиндра джина в основном влияют технологические сопротивление от джинируемого хлопка, значение приведенного момента инерции системы. Учитывая большое значение жесткости муфты между двигателем и пильным цилиндром систему рассматривали как единую, одномассовую. При этом суммарный (приведенный) момент инерции системы по расчетам равен 4,25кгм², а при машинном эксперименте его значение варьировали в пределах 1,5÷8,2кгм². Известно, что при больших значениях приведенного момента инерции системы значительно увеличивается переходной процесс пуска системы. Из рис. 1 видно, что при моменте инерции пильного цилиндра 1,5 кгм² пуск машинного агрегата затягивается до 0,02 сек., а при моменте инерции 8,2 кгм² пуск системы продолжается 0,21сек. С увеличением времени запуска системы возрастает потребная мощность привода. Следует отметить, что увеличение приведенного момента инерции системы приводить более равномерному вращению пильного цилиндра джина в установившемся режиме. Из рис. 1а видно, что при J_п=15 кгм²_, размах колебаний угловой скорости пильного цилиндра 1,45 с^-1, а при J_п=8,2 кгм²_, размах уменьшается до 0,22 с^-1. Поэтому есть необходимость уменьшения значений приведенного момента инерции системы. При этом рекомендуемыми значениями момента инерции пильного цилиндра является (2,6÷3,5) кгм²_.  На рис. 1б представлены графические зависимости изменения угловой скорости пильного цилиндра и потребной мощности электроприводом при вариации момента технологического сопротивления (производительности джина) от хлопка-сырца. С увеличением момента сопротивления от хлопка-сырца от 3,0·10² Нм до 12·10² Нм угловая скорость пильного цилиндра, уменьшается от 76,9 с^-1 до 52,7 с^-1 при J_п=6,2 кгм², а при моменте инерции 3,4 кгм² угловая скорость уменьшается от 77 с^-1 до 66,1 с^-1. Отсюда вытекает, что при больших значениях момента инерции пильного цилиндра с увеличением производительности машины уменьшение угловой скорости пильного цилиндра небольшое (10,9 с^-1). Но, при этом расходные значение мощности возрастает от 12,2 кВт до 46,3 кВт. Если учесть, что на каждый пильный диск приходится 5,56 Нм момента сопротивления от хлопка-сырца, которое соответствует 12,3 кг в п/ч.

Выводы:

1. Аналитическим методом решена задача динамики машинного агрегата с механизмом пильного цилиндра джина. Получена формула для расчета угловой скорости пильного цилиндра для установившегося режима движения.
2. Получены графические зависимости изменения времени пуска системы и размаха колебаний угловой скорости пильного цилиндра в функции приведенного момента инерции системы. Рекомендованы рациональные значения приведенного момента инерции пильного цилиндра J_п=(2,6÷3,5) кгм², при которых обеспечивается уменьшение времени пуска машинного агрегата менее чем за 0,11 с.

Литература

1. Левкович Б.А. «Элементы теория джинирования» Ташкент, Госиздат 1938, 163 стр.
2. Раджибаев П. «Повышение эффективности работы пильного джина с применением секционно-составной колосниковой решетки со сменной рабочей частью». дисс. к.т.н. Ташкент, 1984, 165 стр.
3. Тютин П.Н. «Анализ и совершенствование процесса пильного джинирования применительно к поточной технологии обработки хлопка-сырца машинного сбора» дисс. д.т.н. Кострома, 1985, 406 стр.
4. Котов Д.А. Болдинский Г.И. «О выделении семян из сырцового валика пильного джина». сб. ТТИ, №18, Ташкент, 1964, стр. 67-76

 References

1. Lewkowicz B.A. "Elements of the theory of ginning" Tashkent, the State Publishing . House in 1938, 163 p.
2. Radzhibaev P. "Improving the efficiency of the saw gin using sectional integral grate with replaceable working part." diss. Ph.D. Tashkent, 1984, 165 p.
3. Tyutin PN "Analysis and improvement of saw ginning in relation to the production technology of processing raw cotton collection machine" diss. dts Kostroma, 1985, 406 p.
4. Kotov D.A., Boldino GI "On the selection of the raw seed bead saw gin." Sat. TIT, №18, Tashkent, 1964, pp. 67-76