On model solutions of the initial boundary value problem for the equation of vibrations of thermoelastic plates
On model solutions of the initial boundary value problem for the equation of vibrations of thermoelastic plates
Abstract
This work is devoted to the study and analysis of a model initial boundary value problem for the oscillations of a thermoelastic plate. The main problem is the construction of exact solutions for the given problem. The mathematical model of oscillations is a linear partial differential equation of the third order on the time variable and of the sixth order on the spatial variable with constant coefficients. It should be noted that for the spatial variable the problem is one-dimensional, but the equation contains a mixed derivative for the time and spatial variables. The integral identity is obtained, with the help of which in the general case it is possible to show the violation of the energy conservation law. An algorithm for obtaining explicit solutions of this problem in the form of a functional series is presented. The paper contains illustrations showing the deviations of the surface from the equilibrium position and the dynamics of oscillations at different moments of time.
1. Введение
Задача о колебаниях термоупругих пластин является одной из важных и актуальных задач математики и механики. Такого рода задачи возникают при исследовании динамики пластин, которые подвергаются тепловому или механическому воздействию. Например, термоупругие пластины используются в конструкциях теплообменников, резонаторов или других устройств, где необходимо учитывать как тепловые, так и механические эффекты, которые оказывают влияние на динамику движения. Современные методы анализа математических моделей предлагают разные подходы. Численные методы позволяют найти приближенные решение соответствующей задачи и визуализировать его. Аналитические методы дают непосредственные сведения о решении, что позволяет говорить о предсказании поведения колебательного процесса в будущем. Однако построение аналитического решения является намного более сложной задачей, чем получение численного решения.
Целью данной работы является построение точного решения начально-краевой задачи в виде функционального ряда и анализ этого решения.
Для достижения поставленной цели в работе были решены следующие задачи:
1. Использование модификации метода разделения переменных.
2. Вывод интегрального тождества, которое выражает закон сохранения энергии для уравнения колебаний термоупругой пластины.
3. Исследование влияния параметров уравнения на динамику колебаний термоупругих пластин.
В современной литературе представлены уравнения и частичные решения для подобного класса задач. Данная работа предлагает метод поиска точных решений и метод к решению подобных задач.
В работе исследуются поперечные колебания нити, движущейся с постоянной скоростью. Основное внимание уделено резонансным эффектам, возникающим при таких колебаниях, поскольку они могут оказывать значительное влияние на механику различных инженерных и природных структур.
В работе рассматривается неустойчивость аксиально движущейся упругой пластины. Авторы детально анализируют процессы, приводящие к потере устойчивости, и выявляют ключевые факторы, влияющие на динамическое поведение подобных систем. Проведенный анализ имеет важное значение для понимания характеристик упругих материалов, подверженных аксиальному движению, что особенно актуально в приложениях, связанных с транспортными системами, производственными линиями и аэрокосмической техникой.
Работа посвящена статическому анализу неустойчивости подвижных мембран и пластин, которые взаимодействуют с идеальной жидкостью в аксиальном направлении. Рассматриваемые в исследовании модели помогают глубже понять поведение подобных структур в различных гидродинамических условиях, что может быть полезно при проектировании элементов судостроения, авиационных конструкций, а также гибких материалов, эксплуатируемых в жидкостных средах.
Для более детального понимания методов и вычислительных техник, используемых при исследовании колебательных процессов, особое внимание следует уделить работам , и . Эти исследования содержат подробный анализ типичных уравнений в частных производных, обеспечивая необходимый математический аппарат к моделированию динамических процессов в сложных механических системах.
В работе рассматриваются конкретные методы решения уравнений математической физики, что играет ключевую роль при изучении динамики таких объектов, как балки, мембраны и полотна.
В работе представлены результаты исследований, связанных с численными методами решения задач о колебаниях полотна. Авторы рассматривают различные аспекты гашения колебаний, что особенно важно для понимания поведения движущихся полотен в промышленных системах, таких как ленточные транспортеры, рулонные материалы и гибкие механические конструкции.
Работа освещает методы анализа и подходы к управлению колебаниями струны с применением демпфирующих элементов. Авторы подробно изучают влияние различных типов демпфирования на динамическое поведение струны, что может иметь практическое применение в области музыкальных инструментов, робототехники и виброизоляции инженерных конструкций.
Наконец, в работе анализируются вибрационные характеристики движущихся балок Тимошенко при различных типах закрепления концов. Этот аспект играет важную роль в проектировании и эксплуатации инженерных конструкций, поскольку краевые условия существенно влияют на их динамическое поведение. Изучение данных эффектов полезно при проектировании термоупругих пластин, мостовых конструкций, рельсовых систем и других элементов, подверженных динамическим нагрузкам.
Таким образом, совокупность рассматриваемых работ охватывает широкий спектр вопросов, связанных с динамическими характеристиками движущихся упругих систем, их устойчивостью, резонансными эффектами и методами демпфирования. В этой работе главным приемом для построения решений является проекционный метод, с помощью которого определяются коэффициенты при базисных функциях специальной системы алгебраических уравнений. Применение проекционного метода и более подробные аспекты использования приближений Галёркина можно найти в труде , где автор детально исследовал этот метод, предоставив конкретные примеры решения задач.
Анализу решений уравнений дифференциальных уравнений высоких порядков посвящена работа , где методами теории обобщенных функций в банаховых пространствах исследуется разрешимость в классе распределений с ограниченным слева носителем задачи Коши для дифференциальных уравнений третьего и четвертого порядков с фредгольмовым оператором при старшей производной.
Будем рассматривать уравнение колебаний термоупругих пластин, возникающее в теории колебаний термоупругих пластин :
здесь α, β, k, γ — числовые параметры, которые определяются свойствами материала, а именно:
α — тепловое расширение, влияющее на жесткость пластины;
β — отвечает за тепловые эффекты, определяющие демпфирование, инерционные и диссипативные эффекты
;k — коэффициент упругости, определяющий механическую жесткость и волновые характеристики системы;
γ — коэффициент вязкого демпфирования в термоупругом материале.
2. Методы и принципы исследования
Решение u(x, t), x∈Ω⊂ℝn, t∈ℝ+, уравнения (1) при n=2 определяет амплитуду поперечных колебаний термоупругой пластины, то есть отклонение полотна от положения равновесия в точке x в момент времени t.
В данной работе будем рассматривать упрощенную модель термоупругой пластины, а именно одномерную начально краевую задачу, то есть Ω=[0;l], l>0. С условиями жесткого закрепления на концах. При этом уравнение (1) перепишется следующим образом:
краевые условия для которого определяются равенствами:
и начальными условиями:
3. Построение решения
Будем искать решение в виде u(x,t)=T(t)sinλx. Тогда после подстановки в (2) получим обыкновенное дифференциальное уравнение третьего порядка относительно временной переменной:
Далее, действуя стандартным образом, составим для (4) характеристическое уравнение, которое имеет вид:
Сделаем замену неизвестной
Получим решение этого уравнения с помощью формулы Кардано. Сперва введем параметры:
Тогда алгебраическое уравнение (6) перепишется в виде:
С учетом введенных параметров, заменой
Далее, введем параметр
Формула Кардано дает явные выражения для y1, y2, y3:
где
Возвращаясь к z, получаем
а корни характеристического уравнения (5) определяются формулами
Получив корни характеристического уравнения, можем записать решение уравнения (4):
Откуда получаем общий вид решения
Тогда для уравнения (1) функция u(x,t) выглядит следующим образом:
Лемма 1. Пусть u(x,t) — решение уравнения (2) при F(x,t)=0. Тогда для уравнения (2) справедливо следующее тождество:
где:
Доказательство.
Умножим уравнение на
Пусть:
Тогда уравнение представимо в виде:
Наличие в тождестве слагаемых
4. Основные результаты и обсуждение
В ходе исследования было построено явное решение уравнения колебаний термоупругих пластин в виде функционального ряда с применением проекционного метода, выведедено и доказано противоречие интегрального тождества, показывающее нарушение закона сохранения энергии в данной системе.
Проведенные исследования демонстрируют разнообразие волновых режимов в термоупругих пластинах, находящихся в состоянии колебаний. Экспериментальные изменения параметров α, β, k, γ оказывают значительное влияние на динамику колебаний, что наблюдается при отображении полученного решения на координатной плоскости и задания различных параметров, например:
1. α=0,6, β=6,5, k=1, γ=0,5, C1=1, C2=-1, C3=2,8, x=0,58, λ=22. (см. рис. 1)
2. α=0,6, β=5,4, k=1,9, γ=1,3296, C1=1, C2=-1, C3=2, x=0,438, λ=22. (см. рис. 2)
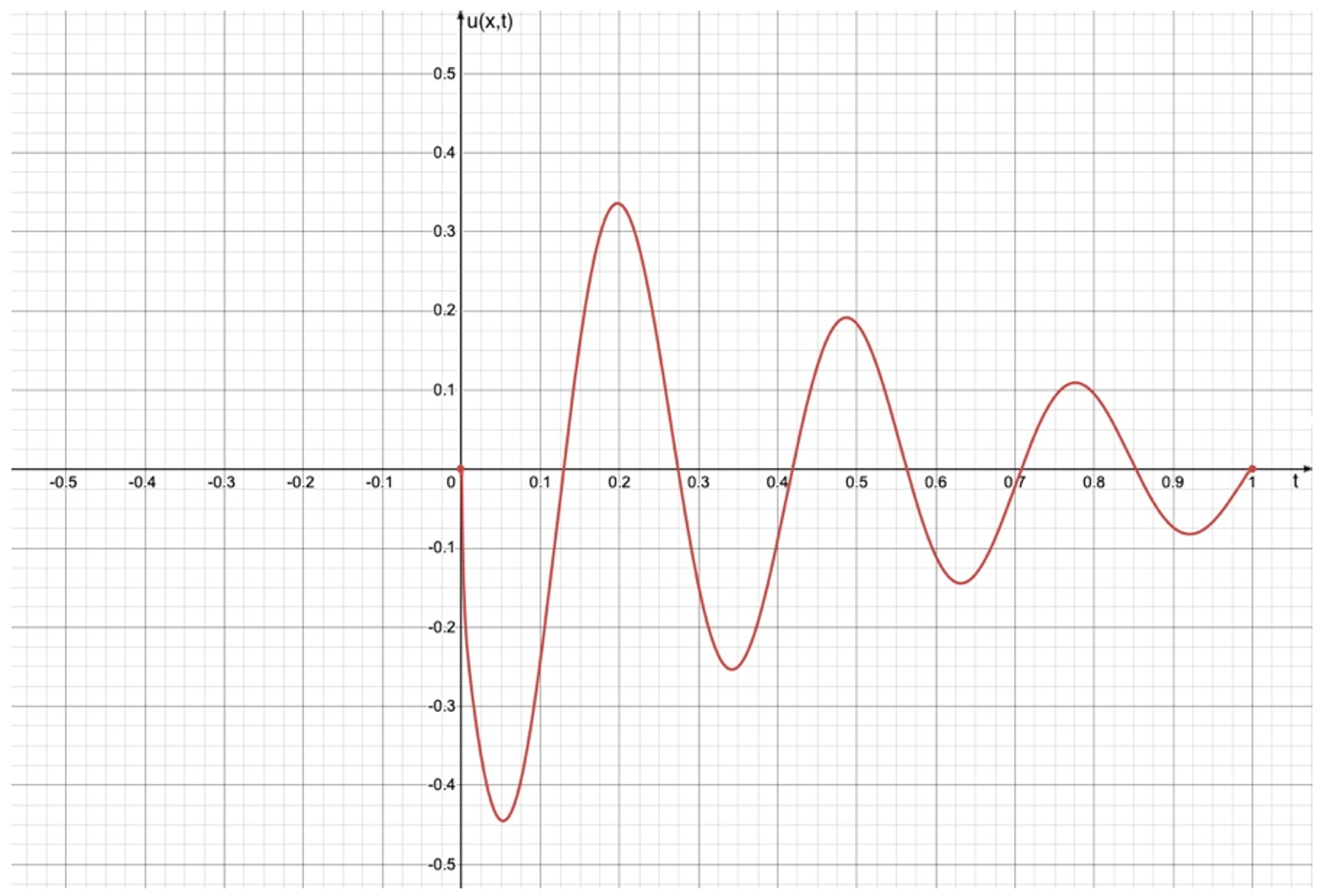
Рисунок 1 - График решения в точке x = 0,58
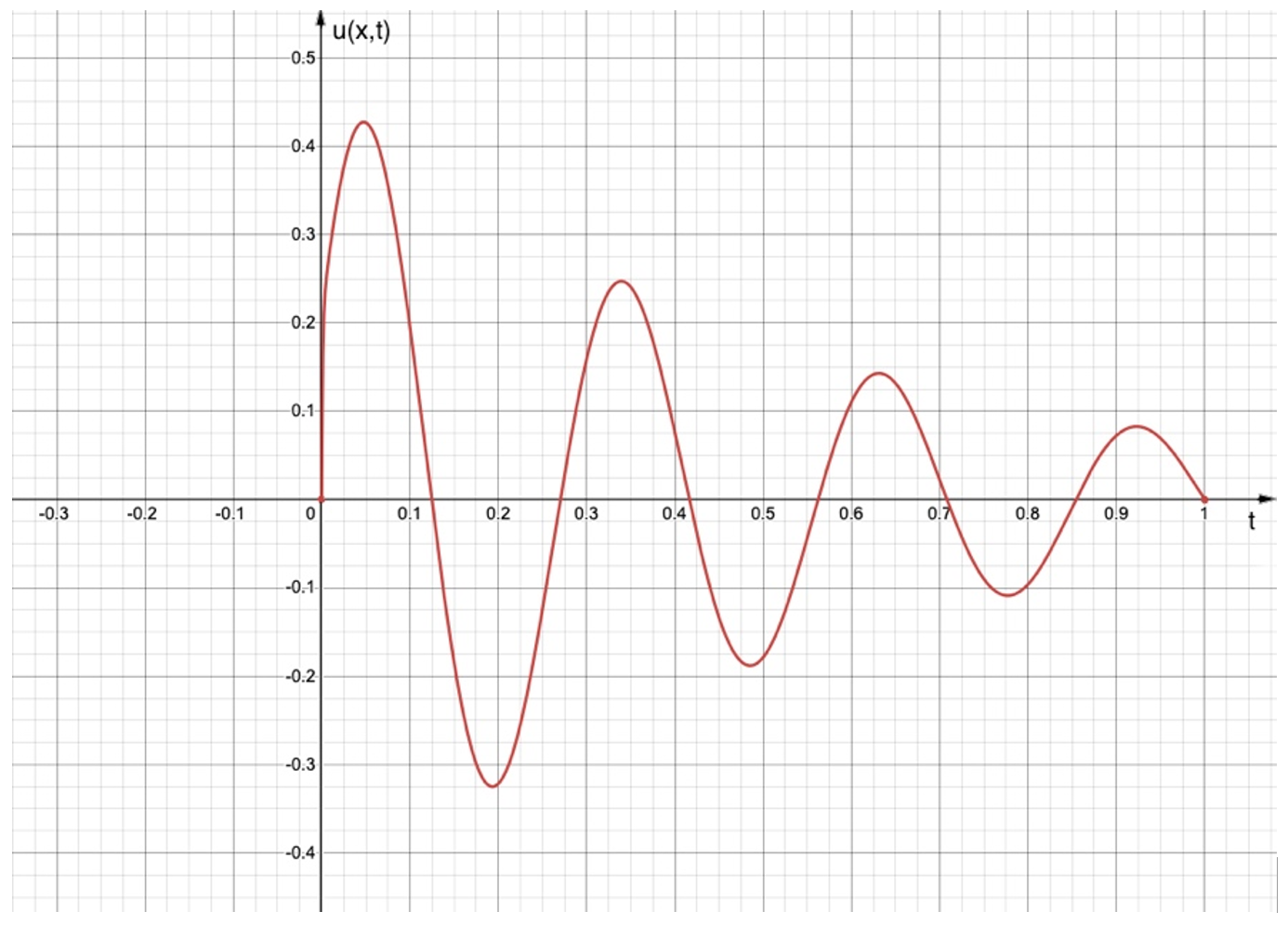
Рисунок 2 - График решения в точке x = 0,438
Результаты исследования представляют значительный интерес как с практической, так и с теоретической точки зрения. С одной стороны, они расширяют понимание физических процессов в термоупругих пластинах с краевыми условиями закрепления. С другой стороны, эти результаты могут послужить основой для разработки новых материалов и технологий, в которых колебательные процессы играют ключевую роль.
5. Заключение
В представленной работе рассмотрены колебания термоупругих пластин, а в качестве математической модели, которая описывает данный процесс рассмотрена начально-краевая задача для уравнения 6-го порядка со смешанной производной с постоянными коэффициентами.
Для рассматриваемого уравнения колебаний приведено явное выражение решения в виде функционального ряда, а также представлено интегральное тождество, которое показывает нарушение закона сохранения энергии. Решение в явном виде для задач такого типа ранее не было известно.
В дальнейшем с использованием найденного в работе решения можно исследовать задачу оптимального управления колебаниями, возникающими в термоупругих пластинах.
