THE ATOMIC MECHANISMS OF DEFORMATION AND FRACTURE OF METALS AND ALLOYS IN HYDROGEN EMBRITTLEMENT

Шашкова Л.В.

Кандидат технических наук, доцент, Оренбургский государственный университет

АТОМНЫЕ МЕХАНИЗМЫ ДЕФОРМАЦИИ И РАЗРУШЕНИЯ МЕТАЛЛОВ И СПЛАВОВ В УСЛОВИЯХ ВОДОРОДНОГО ОХРУПЧИВАНИЯ

Аннотация

Синергетический закон водородной повреждаемости рассмотрен с позиций современных теорий физики пластической деформации и разрушения. Определены ведущие атомные механизмы процессов водородного охрупчивания стали.

Ключевые слова: водородная хрупкость, наводороживание, параметр водородной повреждаемости

Shashkova L.V.

Candidate of technical sciences, assosiate professor, Orenburg State University

THE ATOMIC MECHANISMS OF DEFORMATION AND FRACTURE OF METALS AND ALLOYS IN HYDROGEN EMBRITTLEMENT

Abstract

The synergetic law of hydrogen damageability is considered from positions of modern theories of physics plastic deformation and destruction. Major nuclear mechanisms of processes of hydrogen embrittlement of steel are determined.

Keywords: hydrogen embrittlement, hydrogen charged, parameter of hydrogen damageability

1. Введение

Успехи в решении проблем водородной хрупкости (ВХ) металлов тесно связаны с достижениями науки о прочности и разрушении твердых тел. Традиционно выделяются три основных подхода – феноменологический, структурный и термофлуктуационный (фононный) при общности молекулярно-кинетических явлений. По кинетической термофлуктуационной теории прочности пластическая деформация и разрушение на атомном и субмикроуровне рождаются в одном акте взрывного распада отрицательной флуктуации плотности – дилатона (локальная область растяжения кристалла) при  достижении этой областью критического размера в неравновесных условиях. Активационный (кинетический) и силовой (детерминированный) подходы к разрушению следуют из анализа природы атомной связи в кристалле. Кинетический подход стимулировал развитие термоактивационного анализа процессов деформации и разрушения, изучения двойственной роли пластической деформации при разрушении. Получил развитие структурно-энергетический анализ повреждаемости твердых тел. Известны достижения механики разрушения (теории развития макротрещин) в оценке предельных состояний материалов и конструкций, в том числе в коррозионных средах. Однако механика разрушения испытывает трудности в связи с учетом влияния структуры материалов, существует разрыв между физикой микроразрушения и механикой макротрещин. Определенный прогресс в развитии традиционного детерминированного структурного подхода к разрушению достигнут теорией микроскола. Удалось объединить физику субмикротрещин, структурное металловедение и механику сопротивления конструкций хрупкому разрушению. Структурно-кинетическая теория рассматривает метастабильные состояния,  которые возникают в области концентрации напряжений как особые атом-вакансионные возбужденные состояния кристалла с большим числом степеней свободы и интенсивным массопереносом. Пластическая деформация – это обычный механизм релаксации метастабильных состояний путем рождения и движения различных структурных дефектов. Зарождение пластичного сдвига  –  это локальный кинетический структурно-фазовый переход (диссипативная структура) и может происходить только в локальной зоне кристалла за счет производства энтропии. Деформация развивается многоуровневая, а разрушение  –  крайний механизм релаксации. В микротрактовке разрушения наметилось единство термофлуктуационной и структурно-кинетической концепций зарождения трещин.

Феноменологические закономерности водородного охрупчивания (ВО) сплавов [1] позволили развить физическую теорию хрупкого разрушения наводороженной стали [2-5]. Синергетический закон и структурный параметр водородной повреждаемости [1] рассмотрим с позиций кинетической теории прочности – дилатонной теории флуктуаций слабых (фононных) взаимодействий и структурной дислокационной теории микроскола.

2. Модель микроскола и параметр повреждаемости при водородном охрупчивании стали

Мик­роскол [6] – это первичный источник и главное событие разрушения металлов при их текучести.  Это процесс роста зародышевых субмикротрещин С₃ до крити­ческого размера микротрещины Гриффитса С_Г под действием эффективных касательных напряжений. Под влиянием растягивающих напряжений субмикротрещина теряет устойчивость и способна хрупко разрушить изделие или затормозиться пластической деформацией и стать спутником. Субмик­ротрещины (размер С_З  ≈ 0,2 мкм) являются обычными дефектами структуры металла, как и дислокации, поскольку находятся в упругом равновесии с матрицей и дислокационным скоплением и в процессе под­растания реагируют только на касательные напряжения [6,7]. Согласно [6] размер субмикротрещины С₃, равен:

                                    (1)

где G – модуль сдвига; b – величина вектора Бюргерса;  ν – коэффи­циент Пуассона; d – размер зерна; – коэффициента сброса дислокаций в субмикротрещину; n – чис­ло дислокаций, вошедших в полость зародышевой трещины;  N – общее число дисло­каций в скоплении;  – эффективное внешнее напряжение сдвига.

Взаимодей­ствие дислокаций с точечными дефектами можно характеризовать интегральной величиной – суммарным напряжением сдвига , с которым дефекты действуют на дислокацию [8], увеличивая эффективное внеш­нее напряжение.        Влияние водорода в металле на эволюцию дислокацион­ной субмикротрещины С₃   показано на рис. 1. [2]. Под действием эффективного внешнего напряжения сдвига , размер субмикротрещины С₃ возрастает до размера  за счет облегчения водородом сдви­га дислокаций. Это эквивалентно  увеличению эффективного напряжения  сдвига   на величину .

Рис. 1 –  Схема   подрастания  зародышевой субмикротрещины С_З  за счет облегчения водородом сдви­га дислокаций [2]

Для момента текучести эффективное внеш­нее напряжение  находится из уравнения Холла-Петча как сопротивление границ зерен передаче деформации [6]:

где d – размер зерна, м;   для железа и стали.

Синергетический закон водород­ной повреждаемости [1]: изменение когезионной прочности (прочности на отрыв) DS/S металла, отнесенное к величине большого потенциала внедренного водорода Г (а), определяет вероятность водородного охрупчивания и является структурным параметром ω металлической системы, отражающим ее повреждаемость водородом

 следует из модели микроскола, если предпо­ложить, что диффузионный водород оказывает силовое действие  на дисло­кацию, увеличивая эффективное внешнее напряжение Холла-Петча. С учетом влияния водорода получим [2]:

Сопротивление микросколу S при хрупких разрушениях (микроскол на пределе текучести) вычисляется подстановкой  и  С₃ = С_Г в формулу Гриффитса [6]. Используя , будем иметь [2]:

                 (2)

где  – сопротивление микросколу стали без водорода (коэффициент  [6]).

Приближение   справедливо для

Силовое воздействие водорода на дислокации  в общем случае будет определяться термо­динамическим потенциалом водорода как решеточного газа    RT Г (a, Т) и эффективным активационным объемом  пластической деформации [2,3]:

                                           (3)

где Г (а, T) – функция активности а решеточного газа; N_А – число Авогадро.

После подста­новки выражения (3) в (2) имеем [2,3]:

             (4)

Соотношение (4) совпадает с выражением синергетического закона во­дородной повреждаемости, обоснованного термодинамически и получившего экспериментальное подтверждение [1]:

Уравнение имеет вид типичный для уравнения прочности на разрыв по кинетической концепции прочности. Из формулы (4) находим выражение структурного параметра повреждаемости [2,3]:

                                             (5)

В соответствии с уравнением (5) водородная повреждаемость стали зависит от размера зерна d (структурный фактор) и локализации пласти­ческой деформации, определяемой активационным объемом.

Оценки параметра водородной повреждаемости ω по формуле (5) при d = 10 мкм и = (10 – 500) b³ дают значения ω ≈ 0,3–0,01, что прак­тически наблюдали на конструкционных марках стали [1]. Влияние структурного фактора d на водородоповреждаемость было доказано субструктурной обработкой стали 20: ячеистая субструктура уменьшила водородоповреждаемость ω с 0,05 до 0,015 [9].

Согласно [9], параметр водородной повреждаемости материала ω определяет эффективную энергию активации  разрушения материала в локальной области  –  работу образования критической субмикротрещины:

где – характерная тепловая энергия атомов;  – активационный объем металл-водородного взаимодействия;– критическое напряжение, например, предел текучести .

После подстановки значений: 

где  м; n – число структурных единиц деформации (СЕД); 5b³ – минимальный размер СЕД, связанный с диффузией.

Получим выражение :

         (6)

где = 95 м ^-1/2 в системе СИ.

Соотношение (6) предсказывает величины активационных объемов микропластичности , реально   наблюдаемые   в   системах   металл-водород.   Такие же значения   получаются с помощью уравнения (6) для высокопрочной стали (п = 1-2), у которой  = 0,3 при d = 10 мкм [9].

В условиях синергизма микропластичности на армко-железе наблюдали , в последующем  [10]. Для пластичной стали по уравнению (6) получаются соответствующие значения  при п = 32 (= 0,01, d = 10 мкм) и п = 6 (= 0,05, d = 10 мкм).

Изменение  свидетельствует о реализации разных микромеханизмов пластичности в системах сталь-водород: возбуждение вакансионного диффузионного насоса и двойные перегибы дислокаций, колебания дислокационных струн-сегментов, диффузионно-ко­оперативные явления генерации дислокаций и т. д. [9].

Водород активизирует как диффузионно-вязкий, так и сдвиговый механизм пластичности. Совпадение реально наблюдаемых и расчетных значений   может служить подтверждением правильности подхода (3) – (6), а водородное воздействие на материал в связи с этим можно рассматривать как метод проведения активационного анализа процессов микропластичности и разрушения.

3. Кинетическая теория повреждаемости мигрирующим водородом с позиций реализации дилатонно-фрустронного механизма

Рассмотрим явление ВХ сталей с позиций реализации кинетического дилатонно-фрустронного механизма зарождения субмикротрещин [11-14]. Термофлуктуационная теория моделирует атомный механизм разрушения материалов отрицательными флуктуациями плотности – дилатонами. В твердом теле нагрузка создает метастабильный газ избыточных фононов и возникает критический дилатон, который, поглотив фононы и достигнув предела деформации , кумулятивно распадается в зародышевую субмикротрещину, генерируя дислокации. Как известно [14], критическая деформация образования фрустрона (субмикротрещины) в области локализации сдвига определяется

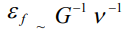                                              (7)

ангармонизмом слабовозбужденных атомов, который учитывается параметром Грюнайзена G, и текучими свойствами среды, которые отражают перенос сильновозбужденных состояний атомов и выражаются через кинематическую вязкость . У хрупких материалов с высокой кинематической вязкостью пластическое течение затруднено и весьма локализовано.

Насыщение стали диффузионно-подвижным водородом увеличивает энергию фононного газа за счет повышения концентрации ангармонических осцилляторов – атомов внедрения, меняет предельные частоты фононов при растяжении - сжатии кристаллической решетки атомами внедрения [15]. Диссипация энергии наблюдается в процессах внутреннего трения и пластической релаксации, что связано с перегруппировкой атомов и дефектов решетки при их взаимодействии и с развитием сдвиговой неустойчивости [16]. Учитывая кинетическое давление решеточного газа на металл и производство энтропии в результате диссипации энергии, произведена оценка прочности системы металл - подвижный водород [17]. Эффекты водородного влияния на металл учтены в уравнении МИ - Грюнайзена состояния твердого тела (кинетическом уравнении прочности) [13,18], которое для условия хрупкой прочности (прочности в условиях, близких к трехосному растяжению) представлено следующим образом:

                        (8)

где –  W энергия фононного газа по Дебаю; D – модуль упругости.

Под действием подвижного водорода увеличивается энергия W фононов, т. е. внутреннее давление, что влечет за собой разупрочнение металла. Разупрочнение металла подвижным водородом является экспериментальным фактом [1]. Диссипация энергии (производство энтропии q), представлена через термодинамические силы  и координаты  ∆Y_i  [17]:

Термодинамическими силами в системе металл - водород могут быть градиенты напряжений и химических потенциалов. В роли термодинамических координат могут выступать изменения в распределении плотности дефектов. Диссипативные процессы микропластичности приводят к закреплению дефектов (старению) и упрочнению [16]. С учетом изложенного хрупкая прочность наводороженного металла представится следующим уравнением [17]:

                                                              (9)

Кинетическое давление решеточного газа передается на металл через колебания решетки, поэтому максимально возможное изменение энергии фононов ∆W положено равным приращению большого термодинамического потенциала решеточного газа  RT ∆Г (a,Т). Вычитая почленно уравнение (9) из (8), получим синергетический закон водородной повреждаемости:

        (10)

Параметр Грюнайзена принят равным предельной деформации ∆V_*/V. Коэффициент  определяет диссипацию энергии в наводороженном металле за счет микропластичности и может изменяться от нуля до единицы (коэффициент диссипации энергии).

У пластичных сталей с низким пределом текучести эффекты переноса и микропластичности при наводороживании будут развиваться легко, так что   → 1, а ω_min → 0. Последнее экспериментально подтверждается. Коэффициент , таким образом, характеризует пластичность конструкционной стали. Величину (1–) можно определить как коэффициент локализации энергии и деформации, пропорциональный величине кинематической вязкости среды . Высокопрочные стали и стали, склонные к локализации деформации, будут иметь → 0 и водородную повреждаемость ω_max = G/β.

Произведена оценка ω_max. Параметр Грюнайзена выражен через термодинамические характеристики твердого тела – коэффициент линейного теплового расширения η, теплоемкость C_V и модуль всестороннего сжатия D [19]:

                                                                                   (11)

Значения параметров, входящих в уравнения (10) и (11), для высокопрочной стали равны [19]: η = 1,15∙10^-5 град^-1;  C_v = 3R;  Т = 300К;  D =169,8∙10³;  S =1500-2000 МПа,  Тогда

       

что соответствует экспериментальным значениям ω_max  [1].

Как известно [11], деформация образования критического дилатона:

                                                  (12)

где а –  атомный размер; G –  параметр Грюнайзена;  –  длина свободного пробега фононов.

Поскольку разнообразие прочностных свойств сведено к зависимости величины  от структурно-химических микронеоднородностей реальных материалов, изучение этой зависимости приобрело первостепенное значение.

По кинетической термофлуктуационной модели прочности и в соответствии с [20] действие водорода можно представить как возникновение внутреннего разупрочняющего фононного давления , определяемого большим потенциалом водорода в металле:

                                    (13)

где –  активационный объем разрушения, равный  согласно [13].

Из выражения (13) следуют уравнение синергетического закона водородной повреждаемости и параметр водородной повреждаемости :

                                         (14)

где S –  сопротивление микросколу;  –  «сжимаемость» материала; –  число деформированных связей в дилатоне.

Формула (14) совпадает с (10) , а коэффициент пластичности приобрел смысл числа п деформированных связей в дилатоне:

    

Таким образом, количественно параметр водородной повреждаемости  металла зависит от двух величин: 1) термодинамической константы Грюнайзена, ответственной за ангармонизм межатомных сил, что предопределяет ведущую роль при водородном охрупчивании поверхности и границ, физико-химических процессов, протекающих на них, поскольку динамика колебаний поверхностных атомов высоко нелинейна; 2) соотношения свойств пластичности α и хрупкой прочности β, которое характеризует склонность к локализации деформации и способность к диссипативным процессам переноса.

4. О единстве термофлуктуационной и структурной концепций зарождения трещин, обусловленных водородом

 Как отмечалось выше, по структурной теории хрупкого разрушения стали сопротивление микросколу равно

                                              (15)

Используя уравнение (15) и численное значение параметра Грюнайзена для стали [17], из соотношения (14) получим

                          (16)

где в системе СИ коэффициент .

Оценка по формуле (16) длины свободного пробега фононов для пластичной малоуглеродистой стали (= 0,01, d = 20 мкм, а = м) дает численное значение см  и  п = 45, что хорошо соответствует результатам [11] для железа:  = (0,11 - 0,16) ∙10 см, т. е. может служить подтверждением справедливости соотношения  (16). Для высокопрочных сталей, наиболее чувствительных к хрупкому разрушению, ( = 0,3) длина свободного пробега фононов в соответствии с условием (16) ограничивается одной-двумя атомными связями.

Из выражений (14) и (16) следует, что параметр повреждаемости стали определяется работой распада критического дилатона

В соответствии с уравнением (16) эта работа зависит от двух факторов  – структурного размера d и числа связей п, свободно пробегаемых фононами, т. е. зависит от критической деформации дилатона, обусловленной структурной и химической микронеоднородностями ма­териала.

Таким образом, водородостойкость  – фундаментальная характеристика мате­риала в теории разрушения. А водородное воздействие является атомным инс­трументом анализа рассеяния фононов на дефектах. Соотношения (14) и (16) количественно выражают величину  через характеристику d реальной микро­структуры и позволяют по параметру  изучать влияние структурных неоднородностей, примесей и других несовершенств на длину свободного пробега фо­нонов. Число п определяет активационную область кооперативных (синергетических) взаимодействий.

Результаты расчета параметра , выполненные по кинетической термофлуктуационной теории разрушения (14), (16) и по детерминированной структурной модели микроскола (6), численно совпадают, если за п в выражениях (14), (16) и (6) принимать одну и ту же величину, например . В таком случае из равенства (14) и (6) следует, что работа локального разрушения (образования субмикротрещин) равна работе микродеформации

                                                            (17)

Этот вывод согласуется с известной концепцией Л. Жильмо [21]. При условии  получаем определение механического концентратора напряжений 

при котором торможение сдвига зарождает субмикротрещину. Механический концентратор равен отношению активационных объемов микропластичности и разрушения, а численное значение  имеет практически наблюдаемый предел. Ограничение  величиной параметра Грюнайзена может свидетельствовать о термофлуктуационном размывании концентраторов напряжений.

Введем в (17) объем дилатона  , тогда

                                                                    (18)

Соотношения (17) и (18) устанавливают взаимосвязь между микропластической деформацией и разрушением: переход от одного микропроцесса к другому означает  изменение на порядок масштаба событий и их параметров (активационных объемов и напряжений). Взаимопереход пластической деформации и разрушения является локальным кинетическим структурным фазовым переходом в достаточно неравновесной системе. На микроуровне ведущими могут быть как процессы разрушения, так и деформации в соответствии с представлениями [21]. Ситуация определяется работой микропроцесса, величина которой согласно выражениям (6), (14), (16) равна  

                                                       (19)

Отметим, что параметр водородостойкости  показывает, во сколько раз работа микродеформации и разрушения превышает характерную энергию kT тепловых  колебаний атомов. Для плотности затраченной на деформацию и разрушение работы  имеем

где   –   универсальная газовая постоянная.

В соответствии с (19) для стали с размером микрозерна  d = 10-20 мкм  водородостойкость будет равна  = 2,7 n. Водородостойкость высокопрочной стали  незначительна ( = 3-5), поэтому, вероятно, что при растяжении ведущими  будут термофлуктуационные скачки имеющихся трещин. В процессе разрушения участвуют п = 1-2 атомных связей, т. е. поверхностный слой микротрещины. Микропластичность ограничивается диффузией в объеме ~ 5a³. Изменение большого потенциала (уравнение 13) объема системы сталь-водород для поверхности микротрещины переходит в поверхностный избыток потенциала  –  уравнение адсорбции Гиббса [22]:

где  – активируемая водородом поверхность; –  индуцированное водородом изменение   поверхностного натяжения;  Ξ – адсорбция;     – энергия хемосорбции водорода, определяемая различием активностей водорода в поверхностном слое и в объеме материала.

У пластичных сталей водородостойкость  = 25-100 и разрушение происходит после реализации разных видов предварительной микропластичности. При этом в соответствии с (19) оценка удельной работы разрушения дает величину = 8000-33000 МДж/м³, что совпадает с известными для железа [23] величинами энергий активации самодиффузии и образования вакансий.

Выводы.

Таким образом, исследованы две физические модели взаимодействия мигрирующего водорода с металлом и рассеяния свободной энергии: 1) кинетическая флуктуационная модель накачки фононами критических дилатонов с микроразрывом металла при напряжениях сопротивления отрыву ; 2) структурная модель индуцированных водородом микронапряжений, которые снижают эффективное напряжение  сдвига дислокаций и облегчают зарождение критической субмикротрещины скола.

Кинетическая модель ВХ предполагает, что хрупкое разрушение происходит по механизму взрыва критических дилатонов и образования микротрещин, а структурная модель исходит из ведущей роли предварительной пластической деформации. Кинетическая модель предсказывает, что максимальная водородная повреждаемость стали определяется параметром Грюнайзена и равна . Такую повреждаемость имеет  высокопрочная  сталь. Модель микроскола предсказывает снижение  с уменьшением размера зерна, что экспериментально подтверждено на стали 20: повреждаемость   снижается с 0,05 до 0,015.

Из уравнения (17) следует, что на микроуровне ведущими могут быть как процессы разрушения, так и деформации, и устанавливает взаимосвязь между микропластической деформацией и разрушением: переход от одного процесса к другому означает изменение на порядок значений активационных объёмов. Ситуация определяется работой микропроцесса, величину которой оценивает параметр водородной повреждаемости ω  по уравнению (19).

При ВХ высокопрочной стали наиболее вероятно реализуется фононная флуктуационная модель разрушения, а пластичные стали разрушаются в соответствии со структурной моделью микроскола. Таким образом, синергетический закон и параметр водородной повреждаемости позволяют выявить ведущие атомные механизмы процессов деформации и разрушения твердых тел при водородном охрупчивании.

Литература

1. Шашкова, Л.В. Синергетический закон повреждаемости металлов и сплавов водородом / Л.В. Шашкова // Международный научно-исследовательский журнал = Research Journal of International Studies. – 2013. – № 7(14). – Ч. 2. – С. 106- 113.

2. Савченков, Э.А. Модель микроскола при водородном .охрупчивании стали / Э.А. Савченков // Известия АН СССР. Металлы, 1990. – № 4. – С. 148-152.

3. Савченков, Э.А. Структурно-кинетические факторы в явлении водородной хрупкости стали: материалы 2 всерос. научнтехн. конф. «Прочность и разрушение материалов и конструкций» / Э.А. Савченков, Л.В. Шашкова. – Орск: Изд-во ОГТИ, 2000. – С. 27-28.

4. Разработка количественной теории водородной хрупкости, создание способов диагностики разрушения и повышения долговечности стали в коррозионно-активных средах / Отчёт по НИР; № гос. регистрации 01860056219; инв. № 02860104903; научный руководитель канд. техн. наук Савченков Э.А.; ответственный исполнитель канд. техн. наук Шашкова Л.В. – Оренбург: ОГУ, – 2001. – 35 с.

5. Савченков, Э.А. Синергетическая концепция водородной повреждаемости металлов и сплавов (этапы развития и перспективы) / Э.А. Савченков, Л.В. Шашкова, Н.А. Манаков // Вестник Оренбургского государственного университета. – 2006. – № 1. – Т. 2. – С. 133 – 137.

6. Мешков, Ю.Я. Структура металла и хрупкость стальных изделий / Ю.Я. Мешков, Г.А. Пахаренко. – Киев: Наукова думка, 1985. – 268 с.

7. Владимиров, В.И. Физическая природа разрушения металлов / Владимиров В.И. – М.: Металлургия, 1984. – 280 с.

8. Петухов, Б.В. Теория влияния точечных дефектов на подвижность дислокаций в потенциальном рельефе Пайерлса / Б.В. Петухов // Известия АН СССР. – 1987. – Т. 51. – № 4. – С. 708-714.

9. Шашкова, Л.В. О связи активационных параметров деформации и разрушения с микронеоднородностью стали при обратимой водородной хрупкости / Л.В. Шашкова // Международный научно-исследовательский журнал = Research Journal of International Studies. – 2012. – № 7(7). – С. 22-27. – ISSN 2303-9868.

10. Скрябина, Н.Е. Некоторые закономерности проявления синергетических эффектов микропластичности при наводороживании железа / Н.Е. Скрябина, Л.В. Спивак, А.Б. Волынцев // Известия АН СССР. Металлы. – 1984. – № 1. – С. 145- 147.

11. Журков, С.Н. Дилатонный механизм прочности твердых тел // ФТТ, 1983. – Т. 25. – № 11. – С. 3119-3123.

12. Физика прочности и пластичности / под ред. С.Н. Журкова. – Л: Наука, 1986. – 260 с.

13. Петров, В.А. Дилатонная модель термофлуктуационного зарождения трещин / В.А. Петров // ФТТ. – 1983. – Т. 25. – № 10. – С. 3124-3127.

14. Олемской, А.И. Синергетика конденсированной среды / А.И. Олемской, А.А. Кацнельсон – М: Едиториал УРСС, 2003. – 336 с.

15. Шашкова, Л.В. Фрагментации перлита стали 20 при нестационарной диффузии водорода / Л.В. Шашкова // Вестник Оренбургского государственного университета. –2007. – № 6. – С. 137-141.

16. Шашкова, Л.В. Синергетические эффекты в неравновесных системах металл-водород / Л.В. Шашкова. – Deutschland: LAP LAMBERT Academic Publishing, 2013. – 105 с.

17. Савченков, Э.А. О водородной повреждаемости конструкционной стали / Э.А. Савченков // Известия АН СССР. Металлы. – 1989. – № 6. – С. 141-145.

18. Журков, С.С. К вопросу о физической основе прочности / С.С. Журков // ФТТ. – 1980. – Т. 22. – № 11. – С. 3344-3349.

19. Лифшиц, Б.Г. Физические свойства металлов и сплавов / Б.Г. Лифшиц, В.С. Крапошин, Я.Л. Липецкий. – М.: Металлургия, 1980. – 320 с.

20. Савченков, Э.А. Отклик конструкционной стали на водородное воздействие / Э.А. Савченков // Известия АН СССР. Металлы. – 1992. – № 4. – С. 202-208.

21. Иванова, В.С. Разрушение металлов / В.С. Иванова. – М.: Металлургия, 1979. – 168 с.

22. Бокштейн, Б.С. Термодинамика и кинетика границ зерен в металлах / Б.С. Бокштейн, Ч.В. Копецкий, Л.С. Швиндлерман. – М.: Металлургия, 1986 – 224 с.

23. Фёдоров, В.В. Кинетика повреждаемости и разрушения твёрдых тел / В.В. Фёдоров. – Ташкент: Фан, 1985. – 168 с.