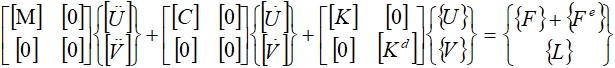DEFINITION OF MODE SHAPES OF ACCELEROMETER
Банников Р.Ю.1, Максимов П.В.2
1Старший преподаватель; 2кандидат технических наук, доцент; Пермский национальный исследовательский политехнический университет
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ФОРМ КОЛЕБАНИЙ МАЯТНИКОВОГО АКСЕЛЕРОМЕТРА
Аннотация
В статье рассмотрен маятниковый акселерометр, для которого решена задача об определении полей перемещений чувствительного элемента с учетом действия электростатический сил. Определены собственные частоты и формы колебаний. Показано, что основными являются первые три формы колебаний.
Ключевые слова: численные методы, динамика, собственные частоты и формы.
Bannikov R.Y.1, Maksimov P.V.2
1Assistant professor; 2PhD in engineering science, associate professor; Perm National Research Polytechnic University
DEFINITION OF MODE SHAPES OF ACCELEROMETER
Abstract
The article describes the pendulum accelerometer. The article describes the pendulum accelerometer for which solved the problem of determining the displacement fields of sensing element with the action of electrostatic forces. Eigenfrequencies and mode shapes are identified. It is shown that the first three of them are basis modes shapes.
Keywords: numerical methods, dynamics, eigenvalues, mode shapes.
Объектом исследования является емкостной микромеханический акселерометр маятникового типа. Датчик предназначен для определения ускорения, направленного перпендикулярно плоскости его основания. Основными элементами прибора являются две пластины, соединенные парой упругих связей. Внешняя пластина является чувствительным элементом акселерометра и называется также маятником, внутренняя крепится к основанию прибора и является неподвижной. На внешней пластине располагается система обкладок, которая в сочетании с электродом, расположенным на корпусе прибора, составляет конденсаторы переменной емкости. При работе датчика внешняя пластина под действием ускорения отклоняется от первоначального положения, величина отклонения определяется путем измерения емкости конденсаторов, изменяющейся при сближении, либо удалении обкладок. Между обкладками конденсаторов возникают силы электростатического взаимодействия, вызванные разностью потенциалов, влияние которых приводит к дополнительному сближению обкладок, при этом величина этих сил зависит от напряженности поля и емкости конденсатора. Акселерометр предназначен для измерения ускорений в пределах от -10g до +10g, где g – естественное ускорение свободного падения. Материал элементов – кремний.
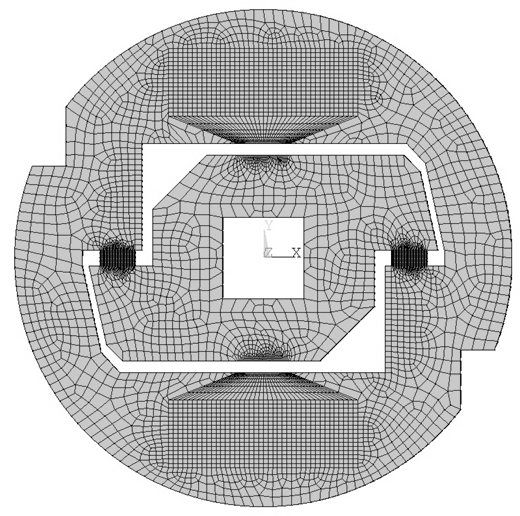
Рис. 1 – Конечно-элементная сетка, построенная в ANSYS
Решается задача об определении НДС, вызванного действием внешних переносных сил инерции, а так же задача об определении собственных частот и соответствующих им форм колебаний. Поставленные задачи решаются численно с применением метода конечных элементов в предположении идеальной упругости материалов. Для решения задач, учитывающих деформирование всех элементов системы, построена трехмерная конечно-элементная модель в пакете ANSYS с мелкой сеткой в области упругих подвесов. Используются 8-узловые элементы SOLID73, имеющие в качестве узловых неизвестных три перемещения вдоль осей и три угла поворота. Конечно-элементная сетка представлена на рисунке 1.
Рассмотрено влияние на статические перемещения чувствительного элемента сил электростатического взаимодействия [1]. Для учета электростатических сил в полученную ранее конечно-элементную модель добавлены области, включающие воздушные зазоры между обкладками конденсаторов. Для решения связанной задачи в ANSYS использовался метод Direct Coupled–Field Analysis. В данном методе для моделирования зазора между обкладками используются специализированные типы элементов SOLID226, содержащие все необходимые степени свободы. Составляется единая система уравнений, описывающая все рассматриваемые модели взаимодействия:
где 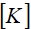 – матрица жесткости,
– матрица жесткости, 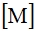 – матрица масс,
– матрица масс, 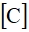 – матрица демпфирования,
– матрица демпфирования, 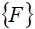 – вектор сосредоточенных и поверхностных сил,
– вектор сосредоточенных и поверхностных сил, 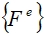 – вектор электростатических сил,
– вектор электростатических сил, 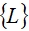 – вектор точечных, поверхностных и массовых зарядов.
– вектор точечных, поверхностных и массовых зарядов.
Решена задача об определении НДС элементов акселерометра под действием ускорения 10g и разности потенциалов 1.5 вольта. Определено, что при воздействии электростатических сил максимальные перемещение маятника изменяются на 14.5 процентов.
С целью определения динамических характеристик рассматриваемого устройства решается задача на собственные значения и определяются формы колебаний конструкции. Конечно-элементная постановка задачи на собственные значения сводится к решению уравнения вида (2):
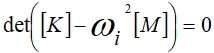 (2) В результате решения получены формы и частоты собственных колебаний. В таблице 1 приведены значения первых шести собственных частот.
(2) В результате решения получены формы и частоты собственных колебаний. В таблице 1 приведены значения первых шести собственных частот.
Таблица 1 – Собственные частоты конструкции
| Номер частоты | Значение, Гц |
| 1 | 13.68 |
| 2 | 428.14 |
| 3 | 455.45 |
| 4 | 5861.84 |
| 5 | 6088.33 |
| 6 | 13983.30 |
Из полученных значений собственных частот колебаний видно, что основную роль в описании движения чувствительного элемента играют преимущественной первые три формы колебаний. Вид первых трех форм собственных колебаний показан на рис. 2.
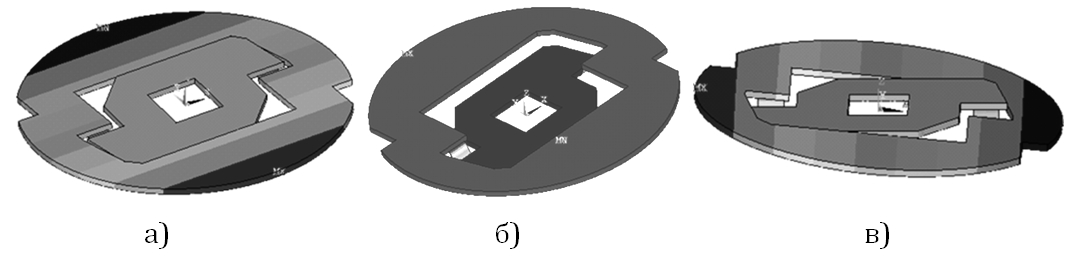
Рис.2 – Собственные формы колебаний системы
а) первая форма; б) вторая форма; в) третья форма
В результате решения задачи на собственные значения определено, что движение чувствительного элемента акселерометра может быть представлено в виде разложения его перемещений по трем формам: поворотов маятника относительно двух взаимно перпендикулярных осей, а также смещения маятника вдоль оси, перпендикулярной плоскости датчика, что позволяет упростить рассматриваемую модель, воспользовавшись методикой, описанной в [2], но сохранив при этом возможность учета локальных особенностей геометрии и физических свойств материала в подвесах маятника.
Работа выполнена при поддержке РФФИ (грант №12-08-31351_мол_а).
Литература
- Мирзина Н.А., Максимов П.В. Аналитическое решение связанной задачи об отыскании поля перемещений чувствительного элемента акселерометра с учетом влияния электростатических сил // Вестник ПНИПУ.Механика. –2009. –№1. С. 112-121.
- Максимов П.В., Сахабутдинов И.Н. Гибридная методика анализа динамических МЭМС-систем и систем с дефектами // Ползуновский вестник. –2013. –№2. –С. 8-11.