ASSESSMENT OF DEFORMATION OF POWER MACHINE DISCS IN THE MANUFACTURING PROCESS
ASSESSMENT OF DEFORMATION OF POWER MACHINE DISCS IN THE MANUFACTURING PROCESS
Abstract
The work presents a methodology for calculation of blade deflections of axial compressor and pump discs. The methodology is based on the basic provisions of the theory of elasticity of circular plates. The method of initial parameters is used as a basis of calculation. The article describes a proposal to replace radial fixing forces by an axial concentrated force.
The replacement methodology is described and the derivation of basic equations describing the influence of fixing forces on the formation and magnitude of axial displacement of the disc web is given. The basic equations for calculating disc deflections are presented.
The article contains a description of the results of experimental research and their comparison with the results of calculations according to the proposed method. Practical recommendations on the use of this methodology are given.
1. Введение
Обработка дисков осевых энергетических машин, таких как компрессора и насосы, неразрывно связана с возникновением погрешностей. Основными причинами возникновения погрешностей являются силы, действующие в технологической системе. К таким силам принято относить составляющие силы резания и силы, действующие со стороны технологических приспособлений. При обработке дисков изготовленных из титановых сплавов в процессе механической обработки резанием возникает потеря геометрической точности его полотна.
В работах
, указано, что сложность изготовления представленных деталей связана с их малой жесткостью, что приводит к технологическим потерям, особенно на начальных этапах освоения производства. Известно , что для уменьшения потерь необходимо снижать режимы резания, тем самым уменьшая силы резания. Но снижение режимов приводит к увеличению времени на обработку деталей, то есть производительность падает.Для оценки точности изготовления требуется провести комплексный анализ степени влияния каждой из указанных сил. Для этого необходимо использовать имеющиеся методики расчета, однако не всегда имеющиеся методики позволяют учесть комплексное действие сил в технологической системе.
При исследовании данного вопроса было установлено, что необходимо уточнить имеющиеся методики расчета, причем обеспечить их прикладной характер. В работах
, приводится описание процессов управления деформациями применительно к корпусным деталям, деталям типа «Вал» и т.д., однако, описание процессов деформирования полотна диска во время обработки недостаточно представлено в литературе.Целью работы является составление математического описания совместного влияния сил в технологической системе на формирование погрешности обработки при изготовлении деталей типа «диск» на этапе технологической подготовки производства.
Задачами исследования являлись определение сил, действующих на обрабатываемую заготовку и оценка их влияния на формирование прогиба полотна диска.
2. Методы и принципы исследования
При проведении расчетов величины деформации полотна диска использовался метод начальных параметров (МНП) , который позволяет численной оценить влияние технологических условий обработки на формирование прогиба полотна диска.
Исходным уравнением метода начальных параметров для расчета является:
К основным положения представленного метода расчета относятся:
1. Вид искомой функции, который должен быть таким, чтобы выражение для каждого (i+1)-го участка содержало в себе слагаемое для i-го участка. При переходе на каждый последующий участок отражает влияние нового силового фактора.
2. Произвольные постоянные отражают физический смысл и их выражают через значения w, Mr, Mq.
Расчеты с использованием МНП необходимо проводить в следующей последовательности:
1. Задать расчетную модель или расчетную схему.
2. Разделить исследуемый образец на некоторое число участков.
3. Выбрать необходимые граничные условия для расчета.
4. Для выбранных участков с заданными граничными условиями записать уравнения.
5. Определить величину прогиба w полотна диска и сравнить ее с допускаемыми значениями.
В случае, когда величина прогиба в точке приложения силы резания составляет более 85% от величины допуска, тогда делается вывод о том, что заданный конструктором допуск не будет выдержан, когда значение величины прогиба не превосходит указанную величину, в этом случае можно сделать вывод о том, что заданный допуск будет выдержан и деталь окажется годной.
Когда допускаемая величина погрешности не превосходит 0,5 мм, тогда расчет величины деформации можно производить, используя уравнение:
где w1 – прогиб от действия силы резания;
w0 – прогиб на внутреннем радиусе диска;
Мr0, Mq0 – моменты, действующие на внутреннем радиусе в радиальном и тангенциальном направлениях, соответственно;
r – текущий радиус, на котором рассчитывается прогиб;
Ру – составляющая силы резания;
ywr, ywP, ywq – сопровождающие функции ;
Е – модуль упругости;
m – коэффициент Пуассона;
h – толщина диска.
Для нахождения w0, Мr0, Мq0 определяются граничные условия, которые напрямую зависят от расчетной схемы. Для различных профилей диаметрального сечения исследуемого диска рассматриваются несколько схем.
3. Основные результаты
На величину деформации заготовки непосредственное влияние оказывают силы, приложенные к заготовке со стороны приспособления. Их действие увеличивает величину осевого смещения полотна диска. При приложении силы закрепления в осевом направлении воздействие на диск будет непосредственным. Величина этого воздействия находится из силового расчета.
На устойчивость полотна диска к прогибам большое влияние оказывает сила закрепления, действующая в радиальном направлении. Устойчивость диска снижается при воздействии сжимающих усилий закрепления.
Увеличение прогиба полотна диска происходит в случае, когда величина силы превосходит критическое значение. Критическую силу можно найти, используя метод Григолюка :
где РЗркр – критическая величина радиальной силы закрепления;
rн – наружный радиус полотна диска;
k1 – коэффициент, зависящий от коэффициента Пуассона.
Радиальная сила закрепления снижает устойчивость полотна диска, а это приводит к увеличению величины его прогиба. Исследованиями установлено, что такую же величину прогиба полотна диска можно получить если увеличить силу резания на некоторую величину, которая будет заменять действие радиальной силы закрепления (рис. 1). Приращение силы называется «эквивалентной силой», которая совпадает с силой резания по направлению, а точка ее приложения совпадает с точкой приложения силы резания.
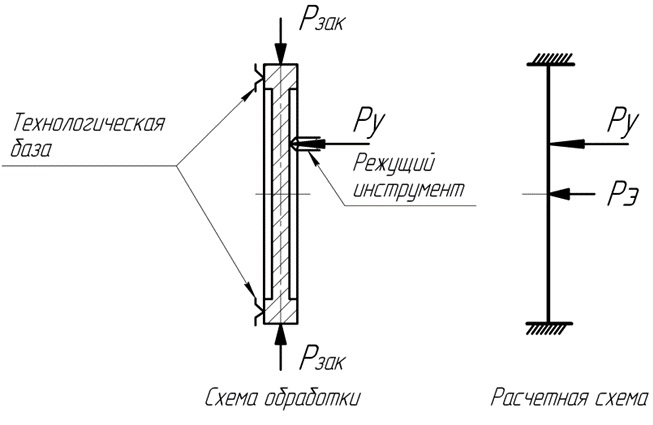
Рисунок 1 - Схема замены радиальной силы закрепления на эквивалентную силу
где er, eq – относительная деформация,
Т – работа внешних сил, которая находится из выражения , :
где РЭ – эквивалентная сила.
В выражении (5) величина прогиба w определяется из следующего выражения , , :
В случае исследования сплошной круглой пластины, внутренний радиус rв=0. Интегрируя выражение (4) в пределах 0 – rн и подстановки в него выражений (5) и (6) получаем следующее:
Ввиду того, что работа радиальных сил переходит в работу внешних сил и приравняв выражение (7) к нулю с последующим сокращением rн2/2, получаем:
Выделив из выражения (8) эквивалентную силу РЭ получим выражение для ее расчета:
4. Обсуждение
Для упрощения расчётов величины прогиба, действие силы закрепления необходимо рассматривать как дополнительную силу, которая действует совместно с силой закрепления. В этом случае уравнение для расчета величины прогиба будет выглядеть следующим образом:
где РЗ – величина силы закрепления, численно равная силе РЭ.
Для непосредственных расчетов величины прогиба полотна диска, с использованием выражения (12), эквивалентная сила РЭ берется со знаком (+) при действии на полотно сжимающих сил закрепления, а при действии растягивающих сил закрепления со знаком (-) , .
Для проверки полученных зависимостей были проведены экспериментальные исследования на специально спроектированном стенде (рис. 2). Результаты измерений приведены в таблице 1.
Таблица 1 - Результаты экспериментальных исследований в случае, когда осевая сила РО = 50 Н приложена в центре полотна диска изготовленного из материала сталь 20
Радиальная сила, Н | Величина прогиба, мм | «Эквивалентная» сила, Н | Величина прогиба, мм |
100 | 0,23 | 1,55 | 0,24 |
200 | 0,25 | 3,1 | 0,25 |
300 | 0,27 | 4,65 | 0,27 |
Полученные данные показали хорошую сходимость расчетных значений и значений, полученных экспериментальным путем (Рис. 3).
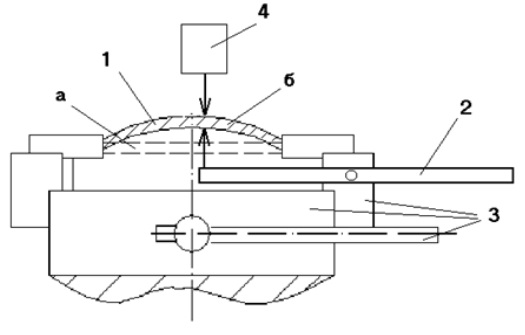
Рисунок 2 - Установка для оценки влияния сил в технологической системе и технологических остаточных напряжений на величину прогиба полотна диска при механической обработке:
1 – исследуемый диск; 2 – механизм нагружения силами в осевом направлении; 3 – механизм нагружения силами в радиальном направлении; 4 – датчик осевых перемещений; а – диск до нагружения; б – диск после нагружения
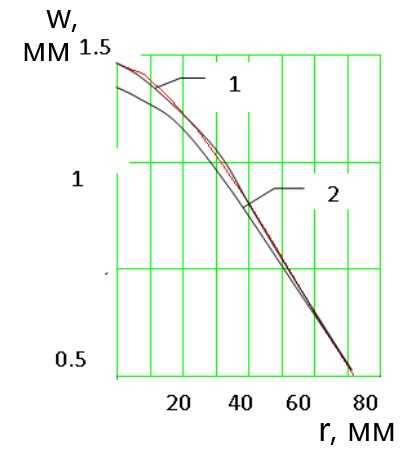
Рисунок 3 - Расчетные (1) и экспериментальные (2) величины прогибов полотна диска при одновременном действии составляющей силы резания РУ и эквивалентной силы РЭ : РУ = 50 Н, Рсж = 190 Н
5. Заключение
В результате выполненной работы были получены базовые уравнения математической модели, которые позволяют установить взаимосвязь между силами в технологической системе и их влияние на величину прогиба полотна диска при механической обработке. Показана возможность замены радиальных сил закрепления на эквивалентную (осевую) силу.
Исследования, проведенные с использованием экспериментального оборудования, позволили установить, что использование такой замены является правомерным. Расчеты величины прогиба полотна диска можно производить с помощью представленных уравнений. Величина погрешности между экспериментальными данными и расчетными значениями составило не более 6%.
Представленная методика позволяет производить прикладные расчеты ожидаемой величины прогиба полотна дисков энергетических машин еще на этапах конструкторской и технологической подготовки производства изделий. Данные расчеты позволят снизить уровень технологических потерь при изготовлении деталей.
