Development of a Mathematical Model of Ferromagnetic Lubricant Flow in a Highly Loaded Wedge-Shaped Sliding Support
Development of a Mathematical Model of Ferromagnetic Lubricant Flow in a Highly Loaded Wedge-Shaped Sliding Support
Abstract
In heavy-loaded friction units for maintenance of high bearing capacity and increase of duration of hydrodynamic mode on working surfaces of sliding bearings, various kinds of coatings are applied.
The research design and development of mathematical models of a wedge-shaped sliding bearing with a non-standard bearing profile adapted to friction conditions and a metallic coating of the guide surface is carried out. The key role here is played by the analytical prediction methodology determining the friction mechanism.
The aim of the study is to develop a mathematical model of wedge-shaped sliding bearing with a non-standard profile of the slider bearing surface and metal coating of the guide surface, taking into account the rheological properties of the ferromagnetic lubricant, depending on the pressure to predict the duration of the hydrodynamic regime of friction.
The task of the study is to develop new mathematical models and analyse the motion of lubricant and melt coating, possessing ferromagnetic rheological properties, in the working gap of the thrust plain bearing with regard to design features to predict the service life of the tribosystem.
The difference of the proposed model from the existing models of metal-coated tribosystems is the presence of an adapted profile and lubricant having ferromagnetic rheological properties and providing reduced wear during start-up and stopping, hence, increased life of tribosystems.
Using the equation of motion of ferromagnetic lubricant, the equation of continuity, the equation describing the profile of the molten contour of the guide, new mathematical models that take into account the design features of the thrust sliding bearing have been derived.
The efficiency of the obtained theoretical computational models was experimentally confirmed.
As a result of the study, new mathematical models for engineering calculations were developed to predict the efficiency, reliability and duration of the hydrodynamic lubrication regime, as well as to determine the main tribotechnical parameters.
1. Введение
В современных условиях математическое моделирование работы трибоузлов и ее прогнозирование при применении антифрикционных покрытий, применение смазки с расплавом с учетом реологических свойств смазки является значимой задачей эффективного поддержания должного уровня готовности высокотехнологической продукции длительных процессов эксплуатации.
Анализ работ , , , показывает, что при проектировании узлов трения необходимо развивать и совершенствовать методологию моделирования подшипниковых узлов. В работах , , , приводятся исследования влияния на процесс трения антифрикционных покрытий контактирующих поверхностей.
Авторы научных статей , , , применяют технологии металлоплакирования для уменьшения силы трения. Установлено, что на прямых отрезках пути снижается износ рабочей поверхности колес, а мощность тяги повышается.
Работы , , , и др. посвящены испытаниям на износостойкость контактирующих деталей в трибосистемах.
В работах , , , проведены исследования трибосистем упорных и радиальных подшипников, позволяющие увеличить на 10–12 % их гидродинамический режим работы.
В научных статьях , , , и др. проанализирована работа трибосистем, что позволило сделать вывод о необходимости применения новых смазочных материалов, конструктивных изменений и совершенствования математических моделей трибосистемы «пятник – подпятник», работающей в экстремальных условиях.
2. Задачи исследования
Рассматривается установившееся течение несжимаемой смазки и смазки с расплавом, имеющих ферромагнитные свойства при работе опоры скольжения «пятник – подпятник». Исследуемая система – клиновидная опора – состоит из ползуна (пятник), нестандартный контур которого наклонен к направляющей (подпятник) под углом α. Направляющая перемещается с заданной скоростью u⃰ в сторону сужения зазора (рис. 1). Решение проведено в декартовой системе координат.
Уравнения контуров поверхностей пятника и подпятника:
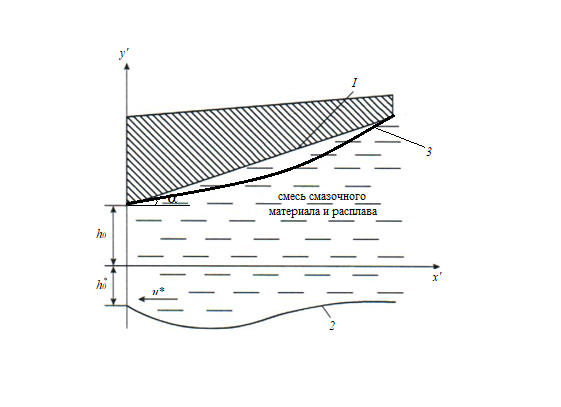
Рисунок 1 - Схематическое изображение упорного подшипника
Примечание: 1 – контур пятника; 2 – контур подпятника; 3 – нестандартный контур пятника
В решении задачи исходим из безразмерных переменных системы уравнений движения ферромагнитной смазки с учетом (2) для случая «тонкого слоя», уравнения неразрывности:
Для поставленной задачи (3) принимаем граничные условия:
где .
Дальнейшие решения поставленной задачи проведем в безразмерном виде:
Запишем асимптотическое решение задачи (3):
Дальше, найдем нулевое приближение решения поставленной задачи, подставив (6) в (3) и применив (4):
– нулевое приближение:
– первое приближение:
Найдем автомодельное решение задачи нулевого приближения по методу , :
Учитывая (11), получим выражение для Ф(x):
Проведем преобразования (9) – (10) аналогично решению (7):
Учитывая (11) и (13), принимая , найдем:
Учитывая (7), (9) и (14), в решении поставленной задачи получим зависимости аналитические выражения для ,
:
3. Анализ полученной математической модели
Проведены проверочные расчеты полученных аналитических зависимостей основных рабочих характеристик исследуемой опоры скольжения с использованием параметров в следующих диапазонах их численных значений: = 10–7 м;
= 0,1256…0,1884 м;
= 0,08…0,101325 МПа;
= 0…1;
= 0,5…16 МПа;
= 49,855…52,657 кН/м2 (применен слой баббита марок Б83, Б88);
= 0,197…0,09501 Нс/м2 (применена смазка ЛЗ ЦНИИ).
Проведено сравнение величин коэффициентов трения предложенной опоры скольжения «пятник – подпятник» при скорости скольжения 1 м/с и изменяющейся нагрузке равной 6…30 МПа. Результаты анализа приведены в таблице 1.
Таблица 1 - Сравнение величин коэффициента трения
№ п/п | Нагрузка | «Пятник – подпятник» | ||
σ, МПа | Поверхности трения стандартные | Баббитовое покрытие | Баббитовое покрытие и нестандартный опорный профиль | |
1 | 6 | 0,0220 | 0,0185 | 0,0172 |
2 | 12 | 0,0165 | 0,0138 | 0,0165 |
3 | 18 | 0,0245 | 0,0110 | 0,00900 |
4 | 24 | 0,0260 | 0,0125 | 0,0101 |
5 | 30 | 0,0300 | 0,0165 | 0,01125 |
4. Экспериментальная проверка расчетных соотношений
Верификация разработанных математических моделей проводилась лабораторно для испытания упорных подшипников на настольно-сверлильном станке (НС-12) на образцах из плоской опоры и сопряженного с ней контртела, имеющего рабочую поверхность, выполненную по специальному некруговому контуру. Покрытие поверхности плоской опоры представляло собой баббит. Результаты экспериментального исследования коэффициента трения при скорости скольжения 1 м/с и нагрузке = 6…30 МПа сведены в таблицу 2.
Таблица 2 - Сравнение величин коэффициента трения (экспериментальная проверка)
№ п/п | Нагрузка | «Пятник – подпятник» | ||
σ, МПа | Поверхности трения стандартные | Баббитовое покрытие | Баббитовое покрытие и нестандартный опорный профиль | |
1 | 6 | 0,0615 | 0,0185 | 0,010 |
2 | 12 | 0,0458 | 0,0128 | 0,0119 |
3 | 18 | 0,0440 | 0,002 | 0,00801 |
4 | 24 | 0,0455 | 0,0125 | 0,0102 |
5 | 30 | 0,0495 | 0,0166 | 0,0134 |
Исследуемые конструкции подшипников скольжения, работающие в гидродинамическом режиме смазывания и компенсирующие, на определенный срок, отсутствие штатного смазочного материала, имеют металлические покрытия, расплав которых выполняет все функции смазочного материала и обеспечивает режим гидродинамического смазывания. Также дополнительно применялся адаптированный к условиям трения опорный профиль контактной поверхности, облегчающий выход подшипника на гидродинамический режим.
Схема экспериментальных исследований включала следующие этапы:
1) работа в режиме гидродинамического смазывания;
2) прекращение подачи жидкого смазочного материала смазывания;
3) работа до полного расхода расплава или разрушения легкоплавкого покрытия.
При этом на компьютере постоянно фиксировалась величина коэффициента трения , а предварительно устанавливалась несущая способность подшипника.
Наличие пленки жидкого смазочного материала имело место только на первом, начальном, этапе при смазывании маслом. Затем на втором, конечном, этапе подача смазочного материала прекращалась, и с ростом температуры подшипник смазывался металлическим расплавом. Гидродинамический режим смазывания сохранялся постоянно.
5. Заключение
1. В процессе проведенных исследований разработаны математические модели (7), (9), (14), (15) упорного подшипника «пятник – подпятник» с нестандартным профилем опорной поверхности ползуна (пятника) и баббитовым покрытием поверхности направляющей (подпятника) с применением реологических свойств смазочного материала и расплава покрытия направляющей, обладающих ферромагнитными свойствами;
2. Проведено теоретическое исследование и экспериментальное моделирование упорных подшипников с поверхностью трения: стандартной; с баббитовым покрытием; с нестандартным профилем опорной поверхности и баббитовым покрытием направляющей;
3. Определены основные рабочие характеристики упорного подшипника для несущей способности и силы трения. Численный анализ полученных аналитических выражений и экспериментальных данных для модифицированной трибосистемы показывает возрастание нагрузочной способности и снижение коэффициента трения;
4. Полученные в результате исследования новые математические модели позволяют в процессе инженерных расчетов прогнозировать эффективность, надежность и продолжительность гидродинамического режима смазывания, а также определять основные триботехнические параметры.
Обозначения:
– угол наклона ползуна к оси Ox;
– начальный зазор слоя смазки;
– толщина баббитового покрытия;
– функция, определяющая контур расплавленной поверхности направляющей;
– обобщенный параметр, характеризующий смазку с расплавом;
– удельная теплота плавления на единицу объема;
– число Гартмана;
– величина, обусловленная наличием электромагнитного поля;
– несущая способность;
– сила трения.
