MATHEMATICAL MODELING OF ECONOMIC GROWTH RESTORATION AFTER THE IMPACT OF AN EXTERNAL SHOCK

В настоящее время разработано огромное количество экономико-математических моделей, которые вполне адекватно имитируют различные макроэкономические процессы в условиях отсутствия внешних шоков. Но современный период времени характеризуется очень высокой турбулентностью. Постоянно возникают финансовые пузыри, эпидемии заразных болезней, военные конфликты, экономические санкции и т.д. В таких условиях наиболее востребованными становятся экономико-математические модели, учитывающие воздействие внешних шоков. Актуальность разработок таких моделей обусловлена: во-первых, необходимостью построения адекватных прогнозов возникновения кризисов; во-вторых, необходимостью моделирования возможных сценариев экономического развития в кризисных условиях; в-третьих, необходимостью выработки конкретных и математически обоснованных антикризисных мер. Математическому моделированию экономики в условиях кризиса посвящено множество научных трудов отечественных и зарубежных ученых. Математические модели развития экономических кризисов и обзоры таких моделей содержатся, например, в работах [1], [2], [4], [5].  

В данной статье будет предложена математическая модель, позволяющая имитировать влияние на экономику внешних шоков, а также способная генерировать антикризисные меры по восстановлению экономического роста и преодолению последствий негативных шоков. Разработка такой модели базируется на современных методах из теории управления хаосом. Практическое применение этой модели будет продемонстрировано на примере российской экономики в условиях введения антироссийских санкций со стороны западных государств. Данная работа является дополнением к экономико-математическому моделированию, проведенному в статье [6].

В работах А.А. Акаева [7], [8, С.46] предложена экономико-математическая модель циклических колебаний деловой активности вокруг трендовой траектории макроэкономического роста

(1)

Здесь , где - текущий объем выпуска продукции (текущий уровень ВВП), - уровень выпуска, соответствующего трендовой траектории долгосрочного экономического роста. Нелинейное дифференциальное уравнение (1) содержит параметры: - скорость реакции запаздывания предложения от спроса, - скорость реакции запаздывания фактических индуцированных капиталовложений от решения об инвестициях, - мощность акселератора, - коэффициент сбережений, - эластичность выпуска по труду, - параметр Оукена, - норма процента, - функция независимых автономных инвестиций.

В модели Акаева (1) предполагается цикличность функции . В этой связи полагаем , где функция является периодическим решением дифференциального уравнения

коэффициенты p, q, μ, ω  - действительные числа.

После ввода обозначений

уравнение (1) принимает вид

Тогда экономико-математическую модель Акаева можно представить следующим образом:

(2)

В целях моделирования влияния внешних шоков на экономику дополним систему (2) «шоковым генератором». За основу возьмем функцию, применяемую в системе Чуа [9]:

Эта функция имеет скачкообразный график и выполняет роль возбудителя хаотических колебаний в осцилляторе Чуа.

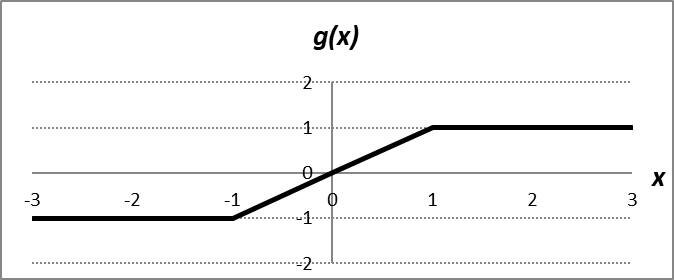
Рисунок 1 - График функции g(x)

DOI:10.23670/IRJ.2022.122.18.1

С математической точки зрения в качестве генератора шоковых воздействий на динамику ВВП целесообразно использовать функцию вида

(3)

Такая функция и варьирование ее параметрами дает возможность моделировать процессы резкого падения объемов ВВП.

В результате дополнения системы (2) «шоковым генератором» (3) получаем следующую модель:

(4)

Представим систему (4) в эквивалентной форме

(5)

В качестве реального примера рассмотрим 5-летнюю выборку статистических данных по ежеквартальным объемам ВВП для России [10].

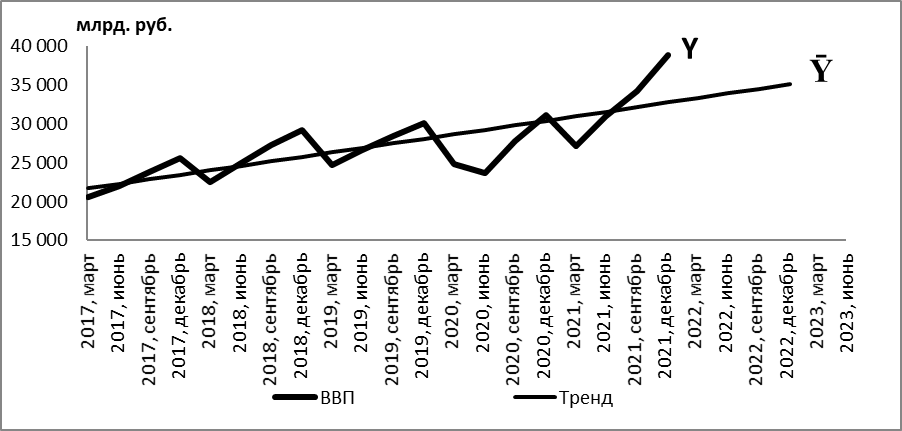
Рисунок 2 - Ежеквартальные объемы ВВП России и линейный тренд

DOI:10.23670/IRJ.2022.122.18.2

С помощью метода наименьших квадратов находится линейный тренд для ВВП:

(6)

Коэффициент корреляции между и составляет 0,78. На рисунке 3 представлен график для .

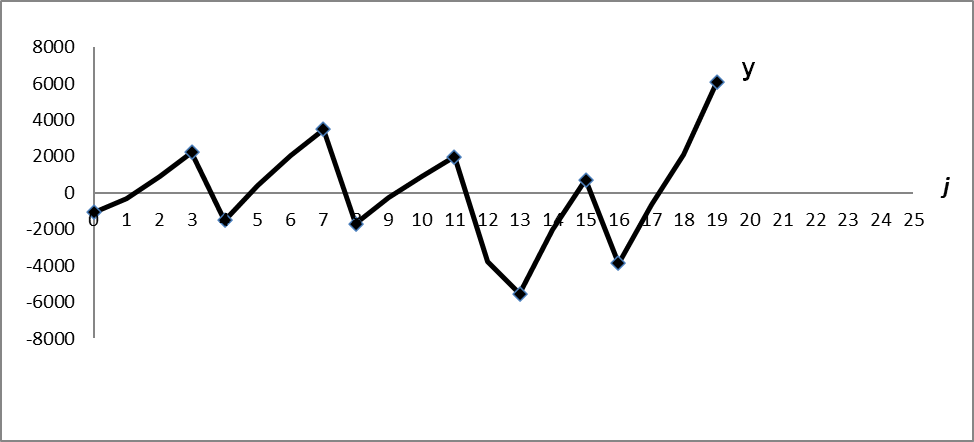
Рисунок 3 - Траектория y

DOI:10.23670/IRJ.2022.122.18.3

Из рисунка 3 видно, что на всем промежутке времени с периодичностью в 4 квартала наблюдаются волны однообразной формы, но различной амплитуды. Для этих волн вычислим среднеарифметические значения локальных минимумов и локальных максимумов (на рисунке 3 обозначены маркером):

Можно говорить, что у обнаруженных 4-квартальных волн усредненный диапазон колебаний составляет от m до M.

В целях моделирования прогнозов по ВВП будем рассматривать систему (5) в качестве базовой. Поскольку мы оперируем дискретными значениями статистики по ВВП, то для моделирования целесообразно перейти от дифференциальных уравнений к разностным уравнениям. Тогда экономико-математическая модель (5) преобразуется в дискретную систему уравнений:

(7)

Покажем, что дискретная система (7) является эффективным инструментом при моделировании циклических процессов в экономике. Из выше изложенного следует, что интерес представляют циклы с периодом 4 квартала. В результате компьютерного эксперимента были подобраны численные значения параметров системы (7):

a = – 0,342597034252971; b = 0,0907420833610221; c = 3,21038961779472;

q = 1,0078742776071; p = 0,187612805894636; ε = – 3,62362849104171;

 δ = 0,492492830231972; ω = 9,99761746105592; μ = 3,00408740862221.

Для нелинейной системы (7) с помощью приближенных методов была найдена периодическая орбита с периодом 4, имеющая следующие координаты:

Важно отметить, что для нахождения этого 4-цикла потребовалось вычислить все его координаты с точностью до 15-го знака после запятой, поскольку решения системы (7) сверх чувствительны к изменениям коэффициентов и начальных данных.

Верификацию полученной модели осуществим с использованием реальных статистических данных по ВВП России [10]. Подберем нормировочные коэффициенты A и B так, чтобы периодическая траектория колебалась в диапазоне от m до M. В результате вычислений получили

и тогда 4-х квартальные циклы, адаптированные к реальной динамике ВВП, моделируются по формуле

(8)

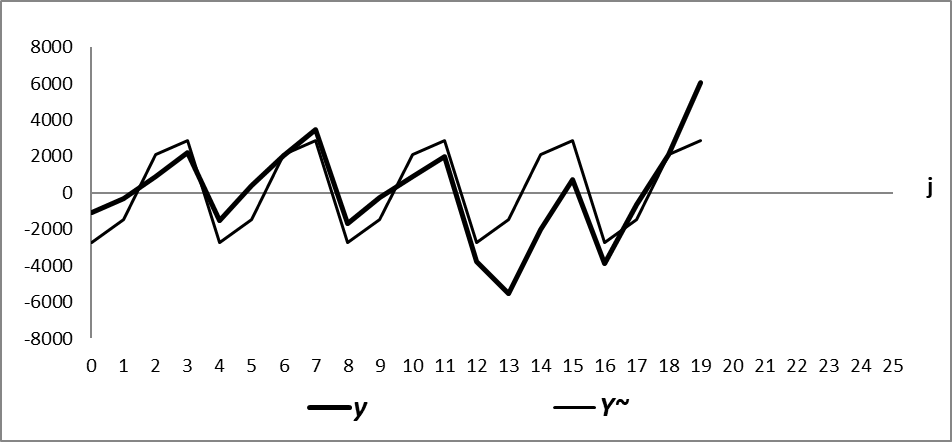
Рисунок 4 - Фактическая траектория y и смоделированная по формуле (8) периодическая траектория

DOI:10.23670/IRJ.2022.122.18.4

Коэффициент корреляции между смоделированными значениями и реальными показателями ВВП равен 0,74 и является статистически значимым, так как по критерию Стьюдента  Тнабл =4,67 > 2,88= Ткрит при уровне значимости α=0,01. Следовательно, дискретная система (7) вполне адекватно моделирует динамику ВВП.

По многочисленным экспертным оценкам, в 2022 году ВВП России может существенно снизиться в результате западных санкций, направленных против российской военной спецоперации на Украине. Например, Центральный банк России [11] прогнозирует это снижение на уровне 8%,   а рейтинговое агентство Moody's [12] оценивает годовое падение российского ВВП в размере 7%.  В этой связи осуществим моделирование влияния санкционного внешнего шока на возможное падение ВВП России  в 2022 году.

Покажем, что за счет варьирования параметров модель (7) способна генерировать сценарии кризисного развития экономики в результате воздействия негативных внешних шоков. Встроенный в модель (7) «шоковый генератор» (3) выполняет роль источника возникновения негативной динамики, а коэффициенты ε и δ являются инструментами настройки в процессе моделирования кризисных явлений.

За счет варьирования параметров ε и δ смодулируем влияние санкционного внешнего шока на динамику российского ВВП.  Как отмечалось выше, система (7) очень чувствительна к изменениям своих параметров. Если к значениям коэффициентов ε и δ добавить малые приращения Δε=–0,00000000198 и Δδ=–0,00000000099 , то система (7) генерирует новое решение , которое с учетом верификационных коэффициентов моделирует новую траекторию . Рисунок 5 демонстрирует, что у полученной траектории периодичность со временем прекращается и переходит в убывание, то есть возникает убывающая динамика ВВП, означающая экономический кризис.

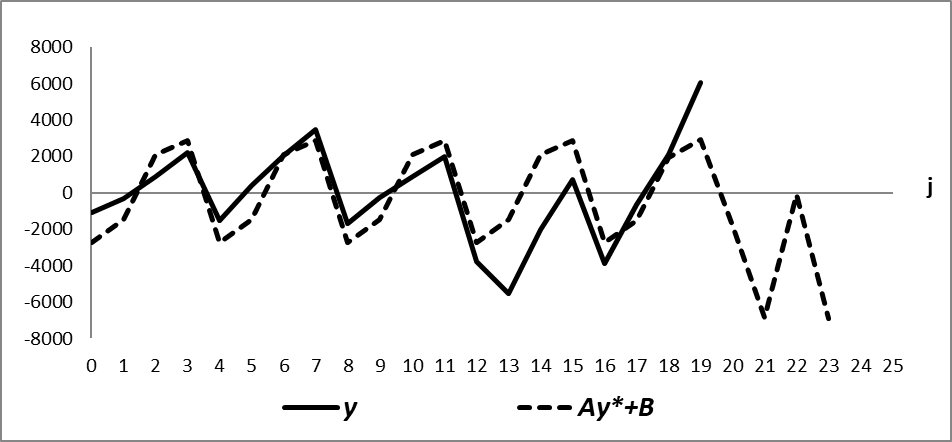
Рисунок 5 - Фактическая траектория y и смоделированная кризисная траектория Ay*+B

DOI:10.23670/IRJ.2022.122.18.5

Поскольку , то получаем формулу для прогнозирования кризисной динамики ВВП:

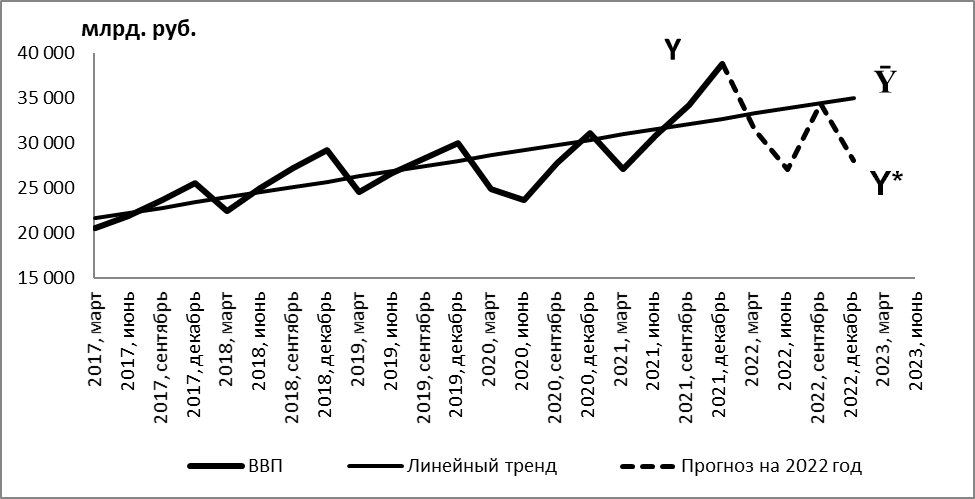
Рисунок 6 - Ежеквартальные объемы ВВП России и кризисный прогноз на 2022 год

DOI:10.23670/IRJ.2022.122.18.6

Согласно кризисному прогнозу, смоделированному системой (7), в 2022 году ВВП России снизится на 7,62%, что соответствует прогнозам Центрального банка России [11] и рейтингового агентства Moody's [12].

Государство заинтересовано в преодолении кризиса, восстановлении экономического роста и возвращении экономики в устойчивый режим развития. С математической точки зрения устойчивому режиму соответствует стационарная (неподвижная) точка системы (7). Для нахождения неподвижной точки решается система

Отсюда неподвижная точка системы (7) имеет координаты

где является корнем уравнения

В целях моделирования способа преодоления ожидаемой негативной динамики ВВП осуществим модификацию модели (7), используя результаты из современной теории управления хаосом. Введем обозначения

и запишем систему (7) в векторной форме:

(9)

где

Поскольку государство заинтересовано в стабильном и устойчивом развитии экономики, то возникает необходимость подавления возможных негативных сценариев. Этого можно добиться за счет применения функции управления U(j) и использования модифицированной системы

(10)

Покажем, что с помощью математических методов современной теории управления хаосом можно сконструировать функцию управления U(j), которая дает возможность эффективно преодолевать влияние внешних шоков и позволяет стабилизировать положительную динамику экономического развития.

Если совершить линеаризацию системы (9) в окрестности найденной неподвижной точки w# с координатами w1#=y#, w2#=z#, w3#=u#, w4#=v#, а затем применить метод Пирагаса [13], то получим модифицированную систему (10), где U(j) является функцией управления, предназначенной для стабилизации поведения решений системы.

На основании результатов работ [14], [15] по стабилизации дискретных систем, получим функцию управления следующего вида:

(11)

Здесь – периодичная матрица следующего вида:

(12)

где , – единичная матрица, – нулевая матрица, – матрица Якоби, – неподвижная точка.

Для рассматриваемой вектор-функции F(w) матрица Якоби имеет следующий вид:

Сконструированная система (10) дает возможность моделировать преодоление кризиса и последующий процесс стабилизации, в результате которой формируется устойчивый режим. На рисунках 7 и 8 представлены смоделированные процессы по устранению последствий санкционного внешнего шока и по стабилизации экономической динамики.

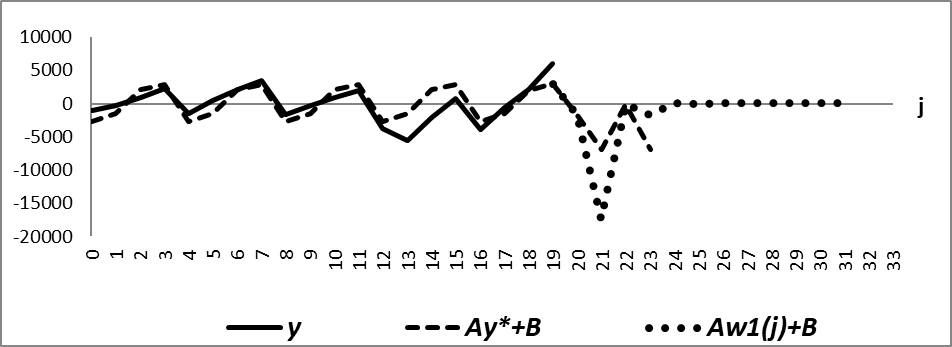
Рисунок 7 - Фактическая траектория y , прогнозируемая кризисная траектория Ay*+B и смоделированная траектория преодоления кризиса Aw1(j)+B

DOI:10.23670/IRJ.2022.122.18.7

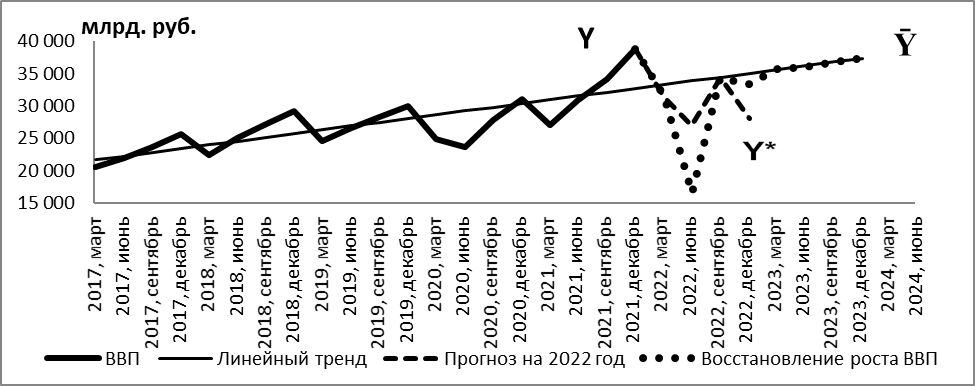
Рисунок 8 - Ежеквартальные объемы ВВП России, кризисный прогноз на 2022 год и смоделированное восстановление роста ВВП

DOI:10.23670/IRJ.2022.122.18.8

Смоделированные процессы получены в результате решения системы (10) с начальными условиями

С учетом верификационных коэффициентов формула для моделирования восстановления роста ВВП имеет вид:

Разработанная модель (10)–(12) является не только инструментом эффективного и адекватного  прогнозирования. Основное достоинство этой модели заключается в том, что она дополнительно дает возможность практического управления динамикой ВВП в целях стабилизации экономического развития. Сконструированная система (10) позволяет моделировать процесс стабилизации за счет функции управления (11). Полученные в явном виде аналитические формулы (11)–(12) позволяют определять размеры и время проведения упреждающих корректировок. На рисунке 9 показана динамика корректирующих операций, направленных на стабилизацию экономического развития.

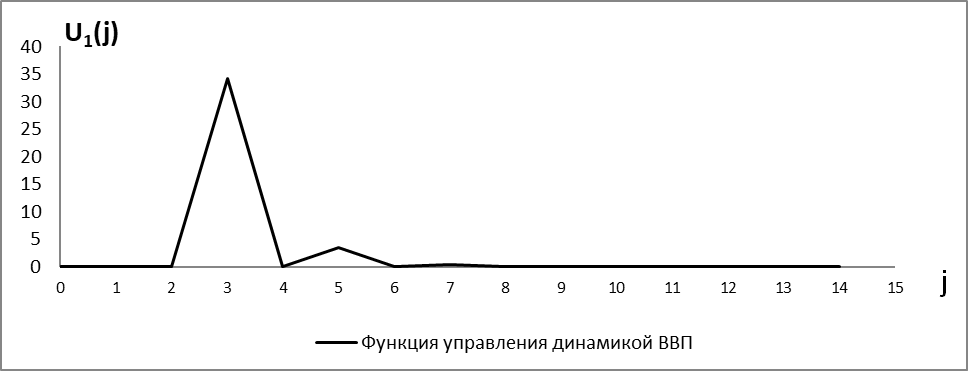
Рисунок 9 - Смоделированная функция экономического управления U1(j)

DOI:10.23670/IRJ.2022.122.18.9

Из рисунка 9 видно, что график для функции управления имеет импульсообразную форму с затухающей амплитудой. Это указывает на то, что оперативные меры по упреждению кризисных явлений имеют точечный характер и их необходимо активно проводить в начальный период, после чего эти меры постепенно сокращаются до нуля. Положительные значения функции управления указывают на необходимость проведения увеличительных мероприятий, а отрицательные значения сигнализируют о необходимости осуществления уменьшительных действий. График функции U1 моделирует поквартальные объемы государственных вложений и частных инвестиций в производственный сектор экономики, которые требуются для восстановления роста ВВП.

В результате верификации, проведенной на основе статистических данных [10] и итогов моделирования, получили поквартальные значения для объемов дополнительных инвестиций, необходимых для преодоления санкционного шока и обеспечения экономического роста. Эти значения сведены в Таблицу 1, которая по сути является графиком проведения превентивных антикризисных мер.

При расчете требуемых объемов инвестиций использовался инвестиционный мультипликатор, который по оценкам экспертов Института стратегического анализа [16] составляет 2,55, то есть в России каждый рубль инвестиций в основной капитал приносит 2,55 рубля прироста ВВП. Из таблицы 1 следует, что для преодоления санкционного шока и обеспечения экономического роста требуется: в 2022 году дополнительно вложить в экономику 8,8 трлн. рублей, а в 2023 году еще 0,97 трлн. рублей.

Разработанная модель (10)–(12) является не только инструментом эффективного и адекватного  прогнозирования кризисной динамики, обусловленной воздействием внешних шоков. Ее основное достоинство заключается в том, что она осуществляет моделирование управленческих рекомендаций и превентивных мер, упреждающих негативную динамику экономического развития.

На основании полученных результатов можно сделать вывод, что для преодоления последствий внешних шоков и восстановления экономического роста необходимо своевременно осуществлять упреждающие корректирующие меры. Предложенная модель (10)-(12) может использоваться как вспомогательный инструмент для стабилизации экономического развития. Формулы (11)-(12) позволяют точно вычислять размеры и время для необходимых упреждающих корректировок. Таким образом, получен инструментарий по моделированию математически обоснованных управленческих мер, направленных на преодоление влияния внешних шоков и обеспечение экономического роста.

Разработанные в данной статье методы довольно удобны с практической точки зрения и легко адаптируются к текущим реалиям. Дискретная система (7) выполняет функцию имитационного моделирования и за счет варьирования параметров генерирует разнообразные сценарии. Модель (10) с управлением (11) позволяет проводить анализ возможностей, способствующих выводу экономической динамики на устойчивую траекторию роста. Полученная модель дает возможность предварительно оценить размеры управленческих решений, направленных на предотвращение кризисных тенденций. Поскольку с помощью формул (11)-(12) можно вычислить точные размеры и время для необходимых импульсообразных корректировок, то модель (10)-(12) может быть полезной при разработке и осуществлении мер, направленных на преодоление воздействия внешних шоков и стабилизацию экономического развития.