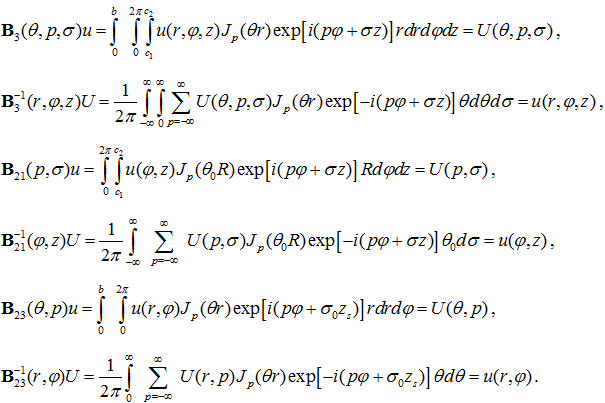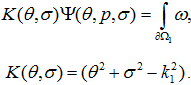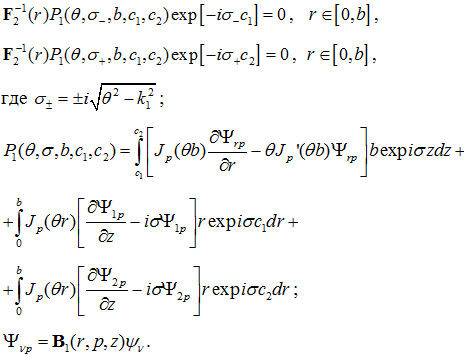ON THE DEVELOPMENT OF FACTORIZATION METHOD FOR THE STUDY OF THE TRANSPORT PROCESS IN COMPLEX STRUCTURED MEDIUM
Зарецкая М.В.
ORCID: 0000-0002-9857-2693, Доктор физико-математический наук, доцент, Кубанский государственный университет
Работа выполнена при поддержке РФФИ (грант № 16-08-00191_а), РФФИ и администрации Краснодарского края (грант № 16-41-230154)
РАЗВИТИЕ ФАКТОРИЗАЦИОННЫХ МЕТОДОВ ИССЛЕДОВАНИЯ ПРОЦЕССОВ ПЕРЕНОСА В СЛОЖНОСТРУКТУРИРОВАННЫХ СРЕДАХ
Аннотация
В настоящей статье представлен факторизационный математический аппарат, предназначенный для исследования процессов переноса субстанций в средах со сложной структурой движения. Он служит дополнением к дифференциальному методу факторизации, если в общую схему плоскопараллельного или иного движения среды включены конвективные ячейки. Полученные результаты могут найти применение в исследовании широкого класса природных и технологических явлений, характеризующихся наличием свободной и вынужденной конвекции.
Ключевые слова: структура, методы, конвекция, моделирование, экология, мониторинг.
Zaretskaya M.V.
ORCID: 0000-0002-9857-2693, PhD in Physics and Mathematics, Assosiate professor, Kuban State University
ON THE DEVELOPMENT OF FACTORIZATION METHOD FOR THE STUDY OF THE TRANSPORT PROCESS IN COMPLEX STRUCTURED MEDIUM
Abstract
This article presents a factorization mathematical apparatus intended for study of transport of pollutants in medium with complex structure of movement. It serves as a complement to the differential factorization method, if the overall scheme of plane or other movement of the medium included convective cells. The results can be used in a wide class of natural research and technological phenomena characterized by the presence of free and forced convection.
Keywords: structure, methods, convection, modeling, ecology, monitoring.
- Одной из особенностей аграрного сектора экономики является его тесное взаимодействие с окружающей средой. Сельскохозяйственное производство, которое в отличие от других отраслей экономики находится в прямой зависимости от многочисленных факторов внешнего окружения, само оказывает существенное воздействие, в том числе, негативное, на качество окружающей среды, прежде всего водной среды и атмосферы.
Среди факторов загрязнения поверхностных и подземных вод отмечают, в первую очередь, транспортные средства, смывы и сбросы промышленных сельскохозяйственных предприятий: минеральные удобрения, инсектициды, пестициды, гербициды, биогены. В атмосферу выбрасываются пыль, угарный и углекислый газы, оксиды серы и азота, углеводороды, радионуклиды.
В атмосферу попадают медь, ванадий, молибден, никель, хром, кадмий, свинец, цинк, опасность которых состоит в том, что содержащаяся в них сажа способствует глубокому проникновению тяжелых металлов в организм человека. Отмечается также рост интереса к радиоактивному загрязнению среды, так как стали выявляться факты острых токсичных эффектов, вызванных загрязнением стронцием и цезием.
Попадая в окружающую среду, загрязняющие вещества (ЗВ), примеси, аэрозоли включаются в глобальную циркуляцию атмосферы и водной среды, могут претерпевать изменения и, в конечном счете, оседают на дно или поверхность водоема или суши, могут участвовать во вторичном переносе, становятся теперь действующим фактором. Специфическое воздействие, оказываемое на элементы сельскохозяйственного производства, может состоять в изменении сортового и видового состава возделываемых культур, токсичном или радионуклеидном загрязнении почв, изменении химического состава почв, генной модификации сельскохозяйственных культур.
Одним из путей оптимизации связей в системе «Сельское хозяйство – Окружающая среда» может стать введение в агропромышленном комплексе производственного экологического контроля (ПЭК) [1]. Среди информационных ресурсов, которыми должны располагать службы ПЭК, нормативные документы в сфере рационального природопользования и охраны окружающей среды, технологические регламенты, информационная база по источникам отрицательного воздействия на окружающую среду, результаты мониторинга качества окружающей среды в зоне возможного влияния агропромышленного предприятия.
Экологический мониторинг, как основной инструмент оценки качества окружающей среды в ПЭК, базирующийся на химико-аналитическом контроле [1], дает возможность только наблюдать и регистрировать изменения параметров и процессов, но не обеспечивает оценки динамики состояния экосистем. Как следствие, возрастает ценность данных о состоянии экосистемы, полученных в ходе комплексного системного мониторинга, включающего в себя также методы прогностического математического моделирования.
- Транспорт загрязняющих веществ в атмосфере или водной среде осуществляется сложными потоками среды, имеющими разные масштабы и структуру. Это могут быть перенос ламинарным плоскопараллельным течением, турбулентное перемешивание или течение вместе с потоком среды, осуществляющим циркуляционное движение. На современном этапе развития методов математического и имитационного моделирования наиболее полно и адекватно описывают процессы транспорта ЗВ в атмосфере и водной среде модели, основанные на решении трехмерного уравнения переноса и диффузии [2, 3]. Несомненным достоинством методов, предложенных в [2, 3], является учет фотохимической трансформации, кинетических процессов нуклеации, конденсации, испарения. Однако область, в которой происходит численное исследование транспорта ЗВ, считается однородной.
На практике, как правило, область, в которой происходит перенос ЗВ, характеризуется наличием сразу нескольких типов структур движения. Например, особенностью крупномасштабной горизонтальной циркуляции вод Черного моря является наличие общего циклонического круговорота, в котором выделяют струйное течение. Ближе к центру моря в этом генеральном течении наблюдаются отдельные вихри. Динамика атмосферы также формируется циклоническими, антициклоническими и плоскопараллельными потоками.
В связи с широким распространением циклонических (конвективных) движений, требуется развитие теории и методов исследования переноса ЗВ конвективными потоками.
- Свободная и вынужденная конвекция являются одним из наиболее распространенных процессов как в природных, так и технологических системах. Поэтому исследование свойств конвективных течений актуально и имеет большую важность, что диктуется многочисленными приложениями в экологии, при исследовании атмосферных и океанических динамических явлений, в геофизике, астрофизике, технических устройствах и технологических процессах.
Конвективные движения жидких и газовых сред изучаются в классической гидродинамике. В основном это численное моделирование на основе уравнений Навье–Стокса, результаты которого широко представлены в публикациях, как в России, так и за ее пределами. Однако решение проблемы существенно затрудняется, если конвективные ячейки включены в общую схему плоскопараллельного или иного движения среды. В этом случае нет возможности применять для аналитического или численного решения один из двумерных или трехмерных методов моделирования, развитых в гидродинамике. Необходимо применять такой метод, который позволяет ставить граничные задачи на основе уравнений движения в различных системах координат для сред, характеризующихся существенно отличающимися механическими, химическими, реологическими характеристиками. Такую возможность предоставляют теория блочных структур и дифференциальный метод факторизации.
В работах [4–7] рассмотрена схема применения указанных методов в общем случае для граничных задач, поставленных в декартовой системе координат. Ниже предложен вариант дифференциального метода факторизации исследования смешанных начально-краевых задач для блочно структурированной среды, отдельные блоки которой формируются внутренними и внешними цилиндрическими границами.
Рассмотрим блочный элемент для внутренней начально-краевой задачи в ограниченном цилиндре Ω радиуса b.
Процесс описывается дифференциальным уравнением Гельмгольца в цилиндрической системе координат r,φ,z :
В соответствии со схемой дифференциального метода факторизации вводим прямое и обратное тройное и двойное преобразования Фурье-Бесселя:
ЗдесьДалее [7] необходимо применить к исходному уравнению Гельмгольца прямые преобразования Фурье-Бесселя, построить внешнюю форму и осуществить переход к функциональному уравнению:
Псевдодифференциальные уравнения представляются в виде
Некоторые вопросы получения систем псевдодифференциальных уравнений для внутренней начально-краевой задачи в ограниченном цилиндре, методы решения и обозначения представлены, например, в работе [8].
Системы псевдодифференциальных уравнений позволяют формировать интегральные уравнения для всех возможных вариантов граничных условий. Решение задачи в интегральном представлении, полученное после обращения псевдодифференциального уравнения, имеет вид:
В результате применения схемы дифференциального метода факторизации [7] получено интегральное представление решения граничной задачи, сформулированной в цилиндрической системе координат. Оно может быть сопоставлено с некоторым процессом, протекающим в режиме свободной или вынужденной конвекции. Согласовывая полученное решение с решением для областей, в которых осуществляется плоскопараллельное движение, можно получить наиболее достоверную общую структуру динамики атмосферы или водной среды и математическую модель переноса ЗВ от некоторого источника, моделирующего, например, предприятие агропромышленного комплекса.
Литература
- Афанасьев В.Н., Суханов П.А., Афанасьев А.В., Максимов Д.А., Перцович А.Ю. Практическое руководство для сельскохозяйственных предприятий по охране окружающей среды /Под ред. В.Н. Афанасьева. – СПб.: СЗНИИМЭСХ, 2005. – 272 с.
- Марчук Г.И. Математическое моделирование в проблеме окружающей среды. – М.: Наука, 1982. – 320 с.
- Алоян А.Е. Моделирование динамики и кинетики газовых примесей и аэрозолей в атмосфере. – М.: Наука, 2008. – 415 с.
- Бабешко В.А., Зарецкая М.В., Рядчиков И.В. К вопросу моделирования процессов переноса в экологии, сейсмологии и их приложения // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2008.– № 3. – С. 20–25.
- Бабешко В.А., Евдокимова О.В., Бабешко О.М., Зарецкая М.В., Павлова А.В., Мухин А.С., Лозовой В.В., Федоренко А.Г. О приложениях теории блочных структур в науках о земле, сейсмологии, строительстве, материаловедении // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2008. – № 4. – С. 27–34.
- Бабешко В.А., Бабешко О.М., Евдокимова О.В., Зарецкая М.В., Павлова А.В., Федоренко А.Г. О дифференциальном методе факторизации в приложениях // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2008. – № 2. – С. 5–12
- Зарецкая М.В., Зарецкий А.Г. Математический аппарат исследования блочных структур с разнотипными блоками // Международный научно-исследовательский журнал. – 2016.– № 3 (45). Часть 2. – С. 58–60.
- Babeshko V.A., Evdokimova O.V., Babeshko O.M. Block elements with a cylindrical boundary in macro-and nanostructures // Doklady Physics. – 2011. – Volume 56. Issue 10. – Pages 544–547.
References
- Afanas'ev V.N., Suhanov P.A., Afanas'ev A.V., Maksimov D.A., Percovich A.Ju. Prakticheskoe rukovodstvo dlja sel'skohozjajstvennyh predprijatij po ohrane okruzhajushhej sredy /Pod red. V.N. Afanas'eva. – SPb.: SZNIIMJeSH, 2005. – 272 s.
- Marchuk G.I. Matematicheskoe modelirovanie v probleme okruzhajushhej sredy. – M.: Nauka, 1982. – 320 s.
- Alojan A.E. Modelirovanie dinamiki i kinetiki gazovyh primesej i ajerozolej v atmosfere. – M.: Nauka, 2008. – 415 s.
- Babeshko V.A., Zareckaja M.V., Rjadchikov I.V. K voprosu modelirovanija processov perenosa v jekologii, sejsmologii i ih prilozhenija // Jekologicheskij vestnik nauchnyh centrov Chernomorskogo jekonomicheskogo sotrudnichestva. – 2008.– № 3.– S. 20–25.
- 5. Babeshko V.A., Evdokimova O.V., Babeshko O.M., Zareckaja M.V., Pavlova A.V., Muhin A.S., Lozovoj V.V., Fedorenko A.G. O prilozhenijah teorii blochnyh struktur v naukah o zemle, sejsmologii, stroitel'stve, materialovedenii // Jekologicheskij vestnik nauchnyh centrov Chernomorskogo jekonomicheskogo sotrudnichestva. – 2008. – № 4. – S. 27–34.
- Babeshko V.A., Babeshko O.M., Evdokimova O.V., Zareckaja M.V., Pavlova A.V., Fedorenko A.G. O differencial'nom metode faktorizacii v prilozhenijah // Jekologicheskij vestnik nauchnyh centrov Chernomorskogo jekonomicheskogo sotrudnichestva. – 2008. – № 2. – S. 5–12
- Zareckaja M.V., Zareckij A.G. Matematicheskij apparat issledovanija blochnyh struktur s raznotipnymi blokami // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. – 2016. – № 3 (45). Chast' 2. – S. 58–60.
- Babeshko V.A., Evdokimova O.V., Babeshko O.M. Block elements with a cylindrical boundary in macro-and nanostructures // Doklady Physics. – 2011. – Volume 56. Issue 10. – Pages 544–547.