DEVELOPMENT ALGEBRAIC LIBRARY FINITE FIELDS FOR GENERALIZED CRYPTOGRAPHIC ALGORITHMS
Приньков А. С.1, Николаев Д. А.2
1ORCID:0000-0003-4983-6477, Студент, 2Кандидат физико-математических наук, Липецкий государственный технический университет
РАЗРАБОТКА АЛГЕБРАИЧЕСКОЙ БИБЛИОТЕКИ КОНЕЧНЫХ ПОЛЕЙ ДЛЯ ОБОБЩЕННЫХ КРИПТОГРАФИЧЕСКИХ АЛГОРИТМОВ
Аннотация
В статье рассмотрена – разработка программной библиотеки конечных полей для дальнейшего использования в качестве алгебраической структуры для ассиметричных схем шифрования на языке Java. Также, в статье представлены UML схема программного комплекса, описание основных классов и результаты апробации разработанного программного обеспечения. Рассмотрены численные методы, используемые при разработке, учитывающие специфику алгебраических структур. Приведен сравнительный анализ, существующих решений.
Ключевые слова: конечные поля, криптосистема, алгебраическая библиотека, криптография.Prinkov A. S.1, Nikolayev D. A.2
1ORCID:0000-0003-4983-6477, Student, 1PhD in Physics and Mathematics, Lipetsk State Technical University
DEVELOPMENT ALGEBRAIC LIBRARY FINITE FIELDS FOR GENERALIZED CRYPTOGRAPHIC ALGORITHMS
Abstract
This article discusses the development of finite fields of software libraries for future use as algebraic structure for cryptographic asymmetric encryption schemes in Java. Also, in the article the UML diagram software package, a description of the main classes and the results of testing of the developed software. We describe the numerical methods used in the development, taking into account the specifics of algebraic structures. The article includes a comparative analysis of existing solutions.
Keywords: finite fields, cryptosystem, algebraic library, cryptography.Криптографические методы считаются надежным способом защиты информации. В связи с колоссально быстрым ростом вычислительной мощности электронно-вычислительных машин возникает потребность в постоянном усовершенствовании средств защиты. В последнее время улучшение криптосистем всё чаще выполняется путем интеграции новых алгебраических структур или изменения характеристик существующих. Здесь и далее, криптосистема - это завершенная комплексная модель, способная производить двусторонние криптопреобразования над произвольными данными. Криптосистема выполняет три основные функции: усиление защищенности данных, облегчение работы с криптоалгоритмом со стороны человека и обеспечение совместимости потока данных с другим программным обеспечением.
Цель данной работы – создать эффективную, обобщенную программную библиотеку, включающую в себя реализацию конечных полей, для использования криптосистемами на языке Java.
Конечное поле, или поле Галуа— поле, состоящее из конечного числа элементов. Наиболее известным примером конечного поля является поле классов вычетов по простому модулю, то есть факторкольцо ![]() . Если F - конечное поле, тогда оно состоит из pn элементов, где простое число p является характеристикой поля, а натуральное число n является степенью поля над его простым подполем. Поля одинаковых порядков совпадают с точностью до изоморфизма. Конечные поля получили повсеместное применение в криптографии. На данный момент на их использовании базируются такие криптосистемы, как схема Эль-Гамаля, алгоритм Чаума, RSA, криптосистема Рабина, схема Шнора и т.д. Их криптостойкость основана на сложности вычисления однонаправленных [1] функций на конечных полях [2]. Построение поля GF(pn) , где p - простое число, n - натуральное число, начинается с построения его примарного подполя (которое совпадает со всем полем при n = 1). Примарное поле строится как кольцо
. Если F - конечное поле, тогда оно состоит из pn элементов, где простое число p является характеристикой поля, а натуральное число n является степенью поля над его простым подполем. Поля одинаковых порядков совпадают с точностью до изоморфизма. Конечные поля получили повсеместное применение в криптографии. На данный момент на их использовании базируются такие криптосистемы, как схема Эль-Гамаля, алгоритм Чаума, RSA, криптосистема Рабина, схема Шнора и т.д. Их криптостойкость основана на сложности вычисления однонаправленных [1] функций на конечных полях [2]. Построение поля GF(pn) , где p - простое число, n - натуральное число, начинается с построения его примарного подполя (которое совпадает со всем полем при n = 1). Примарное поле строится как кольцо ![]() вычетов по модулю p, которое в виду простоты p не имеет делителей нуля и поэтому является полем. Далее построение происходит следующим образом:
вычетов по модулю p, которое в виду простоты p не имеет делителей нуля и поэтому является полем. Далее построение происходит следующим образом: ![]() , где
, где ![]() – неприводимый многочлен над полем
– неприводимый многочлен над полем ![]() .
.
Для разработки был выбран язык программирования Java из-за его кроссплатформенности, популярности. Немаловажно, что подавляющее количество мобильных устройств и серверов работают на виртуальной машине Java. При нынешних темпах развития индустрии портативных устройств и web, потребность в разработке такой библиотеки набирает актуальность. Существуют аналогичные криптографические пакеты. Среди которых большая часть коммерческие и узкоспециализированные (IAIK, JCE, Digt Trusted Java). Другим решением является бесплатный пакет Bouncy Castle. Их общий недостаток отсутствие обобщенности, из-за этого приходится дублировать код в двух случаях: при разработке нового алгоритма и при добавлении алгебраической структуры к уже существующему. Что противоречит стандартам объектно-ориентированного подхода и в дальнейшем приводит к уменьшению стабильности и нарушению целостности библиотеки. У всех этих библиотек, помимо этого, есть и другие существенные недостатки: использование статических структур, отсутствие открытого доступа к алгебраическим модулям, некорректная работа с кириллицей. Главным же недостатком обобщенного подхода является скорость работы, в связи с использованием технологии позднего связывания.
Для начала необходимо спроектировать структуру библиотеки, показанную на рисунке 1. Она составлена в соответствие с классическими определениями абстрактной алгебры [3].
Оцифровка каждого символа (char) алфавита на конечном поле (характеристики p) производится следующим образом:
![]()
С помощью механизма наследования и шаблонов становится возможным использование обобщенных схем шифрования и динамическое подключение алгебраических структур. Под динамическим подключением понимается возможность выбора используемой алгебраической структуры на стадии выполнения программы. Также, данный подход допускает независимое добавление алгебраических структур для криптосистем, при условии согласованности с архитектурой библиотеки. Данная библиотека является полностью независимой и может быть использована любой криптографической системой.
Безусловно, даже при разработке обобщенного программного обеспечения необходимо учитывать специфику реализуемых объектов, как минимум для оптимизации вычислений. Выделим некоторые из использованных численных методов. На полях по определению существуют две операции, и на конечных в том числе. В нашем случае, ресурсозатратными операциями являются умножение и возведение в степень. Умножение возможно оптимизировать с помощью сведения умножения на побитовый сдвиг и поразрядное дополнение, после разложения объекта по двоичному базису на исходном поле. Для возведения в степень целесообразно использовать дихотомический алгоритм возведения в степень, который применим для объектов любой природы. В отличие от возведения по определению (полиномиальная сложность) он характеризуется логарифмической сложностью. Кроме того, для кеширования элементов поля использован паттерн проектирования «Фабрика», что существенно ускоряет вычисления с течением времени использования библиотеки. Следует отметить, что вышеперечисленные методы оптимизация дают наибольший выигрыш при двоичной архитектуре компьютера.
После проектирования реализуем программный комплекс, используя инструменты обобщенного и рефлексивного программирования. В качестве идентифицирующего элемента будем использовать суперкласс Object, все классы являются его подклассами. Для передачи информации между объектами воспользуемся строковым типом, из-за возможности сериализции любых данных в строковые и обратной десериализации. Для оптимизации всех вычислений и генераций будем использовать алгоритмы, приведенные в [4, 5]. Проблема с использованием кириллицы решена посредством увеличения размерности характеристик конечных полей.
Библиотека содержит следующие основные классы и интерфейсы:
- AddSemiGroup – это интерфейс полугруппы по сложению, обязующий реализовать операцию сложения и нейтральный элемент.
- MultSemiGroup – интерфейс полугруппы по умножению.
- AddGroup – интерфейс группы по сложению, дополняющий функцией обращения элемента.
- MultGroup – соответствующий интерфейс группы по умножению. Мультипликативную группу поля образует поле Галуа без нулевого элемента. Эта группа является циклической, то есть в ней есть порождающий элемент, а все остальные получаются возведением в степень порождающего.
- SemiRing, SemiField, Ring – абстрактные классы, реализующие родительские методы, наследуясь от них можно добавить произвольную алгебраическую структуру.
- Field - обобщенный класс поля, реализующий интерфейсы групп по сложению и умножению.
Оценим работоспособность библиотеки (таблица 2) на примере поточного шифрования текста определенной длины криптосистемой Эль-Гамаля, используя реализацию на ЭВМ (таблица 1). Результаты представлены, как среднее арифметическое 500 запусков шифрования.
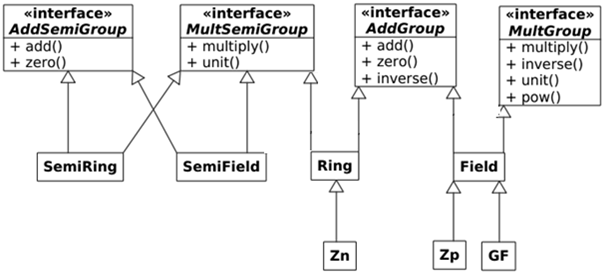
Рис. 1 - Структура алгебраической библиотеки
Таблица 1 - Технические характеристики ЭВМ
| Процессор | CPU CryptoHash | CPU Fibonacci | CPU Blowfish |
| 4 x intel Core i5-4210U 2.7 GHz | 287 | 1.82 | 4.71 |
| Размер текста, символы UTF-16 | GF(pn), секунды | |
| 10 | 0.04 –0.1 | 0.003 – 0.01 |
| 100 | 0.2 – 0.4 | 0.07 – 0.1 |
| 1000 | 0.6 – 0.9 | 0.15 – 0.4 |
| 10000 | 2.2 – 3.5 | 1.3 – 1.9 |
Таким образом, полученные нами данные указывают на реальность практического использования библиотеки. Также, становится заметным что учет специфики конечных полей (Zp и GF(pn)) благоприятно отражается на скорости вычислений.
Литература
- Левин Л. А. Односторонние функции // Проблемы передачи информации. 2003. T. 39. №1. C. 103-117.
- Росошек С. К. Криптосистемы в группах автоморфизмов групповых колец абелевых групп // Фундаментальная и прикладная математика, 2007, том 13, № 3, с. 157-164.
- Винберг Э. Б. Курс алгебры. – Новое издание, перераб. и доп. – М.: МЦНМО, 2011 – 592с. ил.
- Панкратова И. А. Теоретико – числовые методы криптографии. Томск: Томский государственный университет. 2009. 120 с.
- Василенко О. Н. Теоритико – числовые методы в криптографии. М.: МЦНМО, 2003
References
- Levin L. A. Odnostoronnie funkcii // Problemy peredachi informacii. 2003. T. 39. №1. C. 103-117.
- Rososhek S. K. Kriptosistemy v gruppah avtomorfizmov gruppovyh kolec abelevyh grupp // Fundamental'naja i prikladnaja matematika, 2007, tom 13, № 3, s. 157-164.
- Vinberg Je. B. Kurs algebry. – Novoe izdanie, pererab. i dop. – M.: MCNMO, 2011 – 592s. il.
- Pankratova I. A. Teoretiko – chislovye metody kriptografii. Tomsk: Tomskij gosudarstvennyj universitet. 2009. 120 s.
- Vasilenko O. N. Teoritiko – chislovye metody v kriptografii. M.: MCNMO, 2003
