CORRELATION EFFECTS IN SMALL MAGNETIC SYSTEMS
CORRELATION EFFECTS IN SMALL MAGNETIC SYSTEMS
Abstract
Computer simulation of the behaviour of a chain of magnetic atoms described in the framework of the extended Ising model has been performed. Non-magnetic impurity atoms were injected into the sample and the formation of magnetic clusters was examined. The simulation of relaxation processes of the transition between magnetic phases was based on the application of the Metropolis algorithm of the Monte Carlo method. Antiferromagnetic material was placed in conditions favourable to the nucleation of ferromagnetic order (parameters were selected on the basis of phase diagrams) and the relaxation time and the size of forming clusters were monitored. The dependence of the correlation length of the magnetics on temperature and sample size was evaluated using the modelling data. An anomalous behaviour of the spin correlation for samples of finite size at low temperatures was found.
1. Введение
Интерес к низкоразмерным системам обусловлен стремлением мировых технологий к компактности и максимальной плотности функциональных элементов. Производители микросхем анонсировали выход микросхем с использованием производственных норм 3 нанометра. Активно ведется поиск материалов для создания квантовых компьютеров . Повышенный интерес к одномерным конденсированным системам в последние годы обусловлен значительными достижениями в области синтеза и экспериментального изучения нового класса твёрдых тел – квазиодномерных веществ. Они обладают нитевидной кристаллической структурой и ярко выраженной анизотропией магнитных свойств. При этом также развиваются технологии инжекции магнитных атомов на немагнитные подложки и вытягивания тонких магнитных нитей. Возникает необходимость исследования систем состоящей из малого числа атомов, при этом спиновые магнитные эффекты атомов в перспективе могут быть использованы как для хранения, так и для обработки информации. Одним из способов управления физическими свойствами низкоразмерных цепочечных магнитных материалов является инжектирование немагнитных примесей, с целью образования магнитных кластеров. При этом дефектные – немагнитные атомы примеси могут располагаться как случайным образом, так и в определённой последовательности. Их наличие не обязательно приводит к ухудшению физических параметров. Более того, они могут обусловить принципиально новые свойства, которыми идеальная структура не обладает .
Целью нашей работы было ответить на вопрос как осуществляется корреляция в малых магнитных цепочках, насколько сильна взаимосвязь атомов, как влияют внешние и внутренние параметры на критический индекс корреляционной длины. Рассмотреть влияние примесных немагнитных атомов на динамику формирования кластеров.
2. Методы и принципы исследования
Моделирование зачастую становится единственным разумным выбором для исследования ряда объектов и явлений, в которых вычисление статистического интеграла с потенциалом общего вида невозможно . Ввиду того, что модели низкой размерности имеют точное решение (в отличие от трехмерных систем) их изучение позволяет оценить работу приближенных методов и отсеять неподходящие . Одномерные и двухмерные структуры также отражают особенности реальных объектов с анизотропией. Так в трехмерном кристалле может содержаться цепочка магнитных атомов и с точки зрения магнитного взаимодействия можно перейти к одномерной модели. Такая структура реализуется в:[Pt(NH3)4][Pt(II)Cl4], RbCoCl3, CsCoCl3, RbCoBr3, CsCoBr3 . При исследовании подобных структур числовыми методами можно использовать хорошо зарекомендовавшую себя модель Изинга. Учесть дальнее взаимодействие позволяет модификация гамильтониана, при которой вводится связь вторых и третьих соседей:
где J1, J2, J3 – энергия обменного взаимодействия спинов в первой, во второй и третьей координационных сферах соответственно, H – напряженность внешнего магнитного поля, Si – проекция вектора спина на выбранную ось, N – количество атомов в системе, i – номер узла. При этом параметры энергетических потенциалов подбираются на основе экспериментальных данных по низкоразмерным магнитным системам , .
Мы можем провести симуляцию релаксационных процессов при переходе между магнитными фазами используя алгоритм Метрополиса метода Монте-Карло и детально рассмотреть образующиеся магнитные кластеры и их параметры. Дефекты реальных кристаллов учитываются введением в модель узлов, не участвующих в магнитном взаимодействии. Они моделируют примесные атомы, или атомы базового кристалла, не обладающие магнитными свойствами, но встроившиеся в цепочечную структуру.
Шаг алгоритма связан с опрокидыванием спина магнитного узла и расчетом вероятности подобного перехода (энергетическая оценка и учет случайных флуктуаций). Данный метод позволяет смоделировать тепловые колебания атомов в образце . При этом нами учтена возможность компьютеров генерировать лишь псевдослучайные числа и заложен запас шагов алгоритма на частицу, позволяющий снизить относительную погрешность метода. Начальное состояние одномерной решетки задавалось как антиферромагнитное, далее (параметры подбирались на базе фазовых диаграмм) образец помещался в условия, благоприятствующие зарождению ферромагнитного порядка, и отслеживалось релаксационное время и размер формирующихся кластеров.
3. Основные результаты
В квазиодномерных магнетиках при фазовых магнитных переходах проявляются корреляционные эффекты. Удивительно, но такое «ощущение» частицами друг друга зачастую превосходит радиус энергетического взаимодействия. При этом близость к критической температуре усиливает флуктуации и корреляционную длину, делая заметными многочастичные взаимодействия . Степень зависимости корреляционного радиуса (внутри него частицы «чувствуют» друг друга) от температуры описывается индексом корреляционной длины ν. Для его вычисления использовалась формула малой разности температур (Т→Tc):
где параметр τ указывает на удаленность температуры от критической. Или
В одномерной модели Изинга критическая температура определена как нулевая: Tc=0, поэтому
Вблизи критической области возникает существенное взаимодействие флуктуаций, определяющее особенности критического состояния. Можно указать характерный параметр системы – корреляционный радиус, за пределами которого перевороты спинов происходят статистически независимо, а внутри элементы остаются связанными между собой. Его можно рассчитать как среднее значение длины самого большого кластера частиц с ферромагнитным упорядочением в статистическом наборе магнитных конфигураций.
Результаты моделирования представлены в виде графиков. В области низких температур реализуются аномальные области, где магнитный кластер охватывает все возможные атомы, и его длина совпадает с размерами цепочки (рис. 1, а). При этом рост температуры не оказывает влияние на корреляционный радиус в границах данной области. Размеры аномальной области сужаются при увеличении геометрических размеров образца и проявляются только на сверхнизких температурах. При рассмотрении удельной корреляционной длины виден постепенный выход из аномальной зоны для низких температур (относительная температура Т<0,5). С повышением температуры атомы двигаются более интенсивно и магнитные кластеры формируются меньшего размера (рис. 1, б).
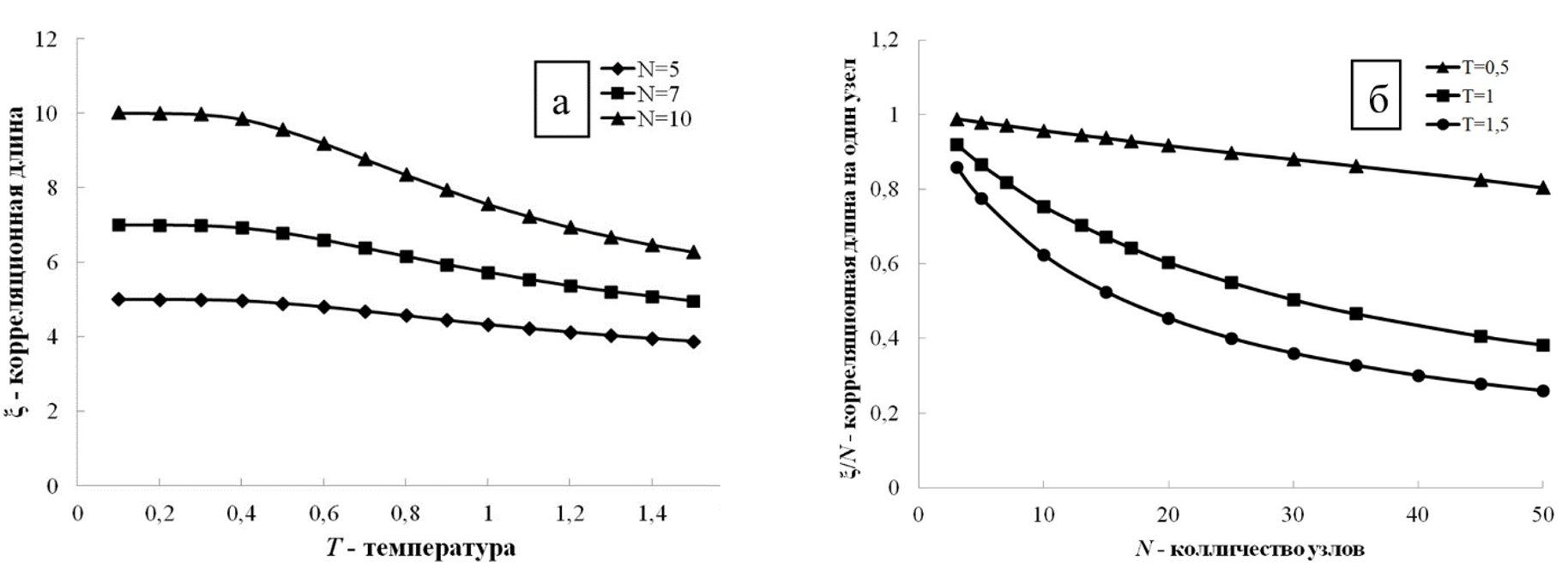
Рисунок 1 - Графики зависимости
Примечание: а) корреляционной длины ξ от температуры б) корреляционной длины на один узел ξ/N от размеров системы (H=0, J2=0)
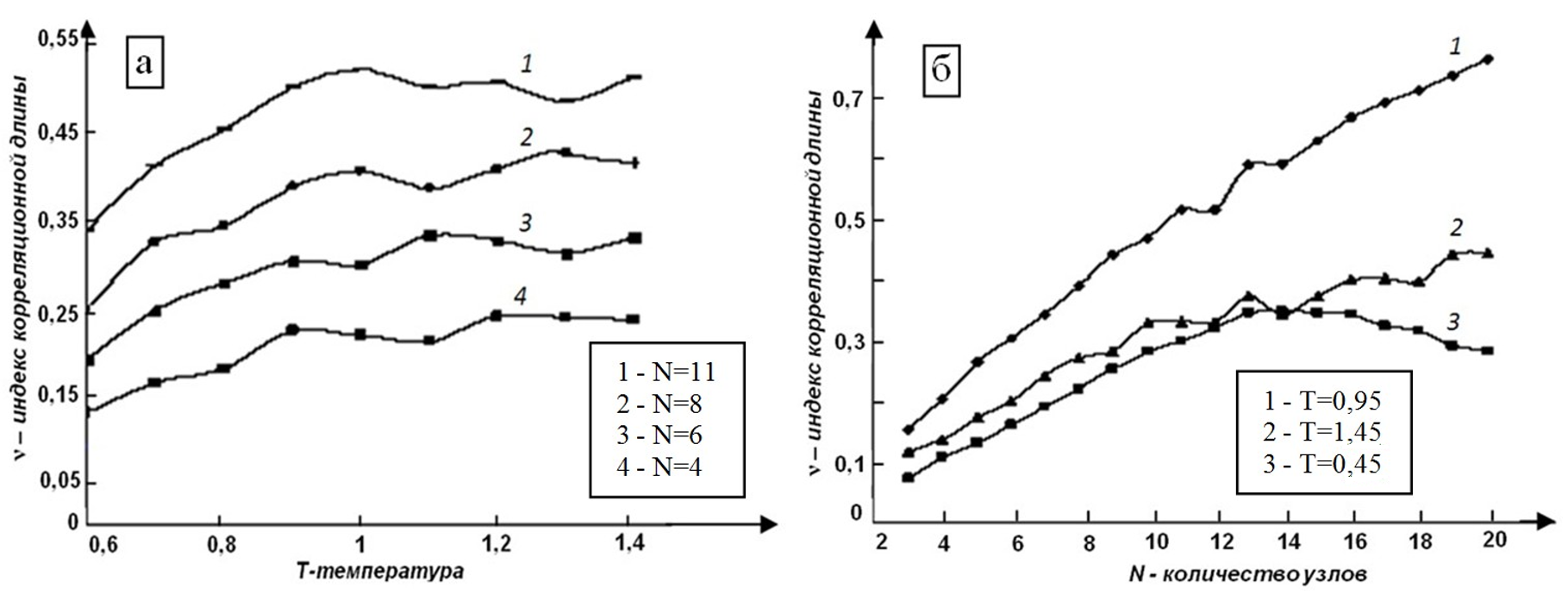
Рисунок 2 - Зависимость индекса корреляционной длины
Примечание: а) от температуры, б) от числа узлов
4. Заключение
Таким образом, при слабых тепловых колебаниях (Т<0,5) на решетке конечного размера индекс корреляционной длины меньше теоретических значений (считается для бесконечной модели), при этом он практически не зависит от температуры. При рассмотрении модели с большим числом атомов наблюдается сужение критической области (для бесконечных теоретических систем эта область сводится к точке
). При дальнейшем увеличении температуры радиус корреляции приобретает монотонную зависимость от длины цепочки атомов. Влияние внешнего магнитного поля на индекс корреляционной длины неоднозначно. Если напряжённость поля мала, то увеличение напряжённости приводит к увеличению значений индекса. Однако при дальнейшем увеличении магнитного поля наблюдается монотонное уменьшение индекса (рассматривалась промежуточная область температур 0,5<T<3). С ростом энергии взаимодействия во второй координационной сфере зависимость корреляционной длины от температуры становится более слабой. Введение в цепочку спинов немагнитных атомов примеси приводит к уменьшению как корреляционного радиуса, так и критического индекса ν.