ВОЗМОЖНЫЕ СТРУКТУРНЫЕ СОСТОЯНИЯ ДЕТЕРМИНИСТИЧЕСКИХ МОДУЛЯРНЫХ СТРУКТУР С ФРАКТАЛЬНОЙ КОМПОНЕНТОЙ В 2D ПРОСТРАНСТВЕ

Иванов В.В.

Кандидат химических наук, доцент, Южно-Российский государственный технический университет (Новочеркасский политехнический институт)

ВОЗМОЖНЫЕ СТРУКТУРНЫЕ СОСТОЯНИЯ ДЕТЕРМИНИСТИЧЕСКИХ МОДУЛЯРНЫХ СТРУКТУР С ФРАКТАЛЬНОЙ КОМПОНЕНТОЙ В 2D ПРОСТРАНСТВЕ

Аннотация

Обсуждаются возможные структурные состояния детерминистических модулярных структур с фрактальной компонентой в 2D пространстве.

Ключевые слова: структурное состояние, модулярная структура, детерминистическая фрактальная структура.

Ivanov V.V.

PhD in Chemistry, associate professor, South-Russian state Еngineering University (Novocherkassk Polytechnic Institute)

POSSIBLE STRUCTURAL STATES OF DETERMINISTIC MODULAR STRUCTURES WITH FRACTAL COMPONENT IN 2D SPACE

Abstract

The possible structural states of deterministic modular structures with fractal component in 2D space were discussed.

Keywords: structural state, modular structure, deterministic fractal structure.

Представление основных классов возможных структурных состояний локальной структуры в ячейке структурированного 2D пространства основано на следующих предположениях.

1. Структурные элементы ячейки 2D пространства - результат локального проявления вполне определенных структурных элементов 2D ячейки одного из подпространств 3D пространства [1, 2].
2. Структурное состояние в ячейке может быть обусловлено как кристаллическими компонентами r подструктуры R², так и ее возможными фрактальными компонентами f [3 - 10].
3. Кристаллическая компонента r модулярной структуры R² может быть определена как с помощью дискретной группы трансляций {t_i}, так и с помощью непрерывной группы трансляций {τ_i} (i = 1, 2) [4 - 6, 11 - 16].
4. Фрактальная компонента f структуры R² может быть определена как i-модулярная гибридная структура (в общем случае i = 1, 2) с помощью соответствующих своих генераторов (точечных, линейчатых или их возможных комбинаций) [17 - 24].

Проанализируем вероятные структурные состояния с учетом кристаллической и фрактальной компонент. Структурные состояния R^2 _- подструктур соответствующей R³ структуры (рис.1): - структура R ³_2r1f (r₁ , r₂ , f) - R²-подструктуры: R²_2r(r₁ , r₂), R²_1r1f : (r₁ , f) и (r₂ , f), - структура R³_1r2f (r₁ , f₁ , f₂ ) - R²-подструктуры: R²_1r1f(r₁ , f₁ ) и (r₁ , f₂ ), R²_2f: (f₁ , f₂ ), - структура R³_3f(f₁ , f₂ , f₃ ) - R²-подструктуры: R²_2f: (f₁ , f₂ ), (f₁ , f₃ ) и (f₂ , f₃ ). С учетом характера элементов группы трансляций ячеистого 3D пространства, а также возможных топологических размерностей модулей фрактальных структур получены основные классы вероятных фрактал содержащих структур ячеистого 2D пространства (рис.1). По своим индивидуальным геометрико-топологическим характеристикам и размерности структуры разных классов существенно отличаются между собой. Очевидным образом это проявляется в локальных размерностях структуры 2D пространства с разными структурными состояниями. Будем принимать во внимание следующее:  

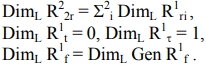
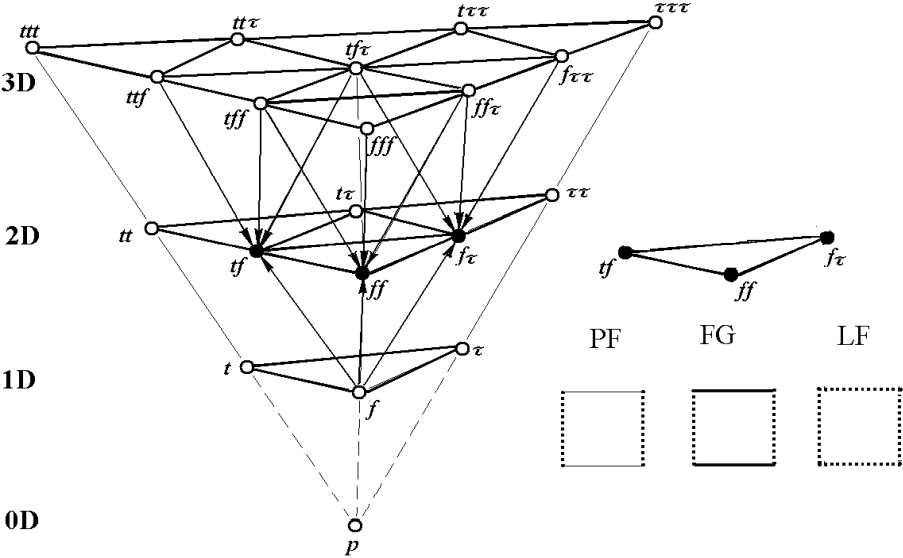Рис.1 – Схема взаимосвязей возможных структурных состояний объектов в 1D – 3D пространствах (t, τ и f – кристаллическая, линейчатая и фрактальная компоненты структурных состояний, соответственно; PF, FG и LF – основные классы фрактал содержащих детерминистических структур в 2D пространстве: точечные, гибридные и линейчатые). В этом случае локальные размерности структур могут быть определены следующим образом: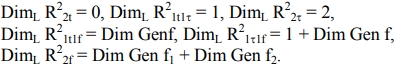

Следует отметить, что глобальная размерность структур только с кристаллической компонентой состояния Dim_G R²_2r=2. Однако, если присутствует хотя бы одна фрактальная компонента состояния структуры, то тогда глобальная размерность ее Dim_G R²_2r<2. В качестве примера приведем элементарные ячейки детерминистических предфрактальных структур на основе итерационной последовательности IC(1/2) и канторова множества точек CM(1/3) вида R²_2f  (рис.2). Элементарные ячейки соответствующих им модулярных структур вида R²_1t1f, R²_1τ1f  и R²_2f с минимальными периодами идентичности в 2D пространстве с указанием их группы симметрии G²₂ и количества занятых пространственных ячеек представлены там же (рис.2, б-г).

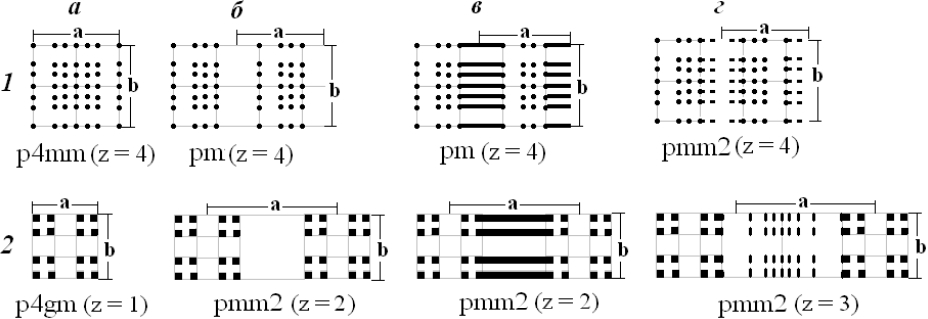Рис.2 – Элементарные ячейки детерминистических предфрактальных структур IC²(1/2) (1,а) и CM²(1/3) вида R²_2f  (2,а), а также возможные на их основе элементарные ячейки модулярных структур вида R²_1t1f, R²_1τ1f  и R²_2f  с минимальными периодами идентичности (б - г). Все приведенные детерминистические структуры являются невырожденными модулярными структурами. Это означает, что каждая из них – представитель множества слоистых модулярных структур, состоящих из набора одних и тех же модулей в определенном соотношении, но с разным их позиционным упорядочением в ячейках 2D пространства. Модулярные структуры каждого множества являются политипными модификациями исходной невырожденной структуры с фрактальной компонентой и обладают близкими геометрическими свойствами [6].

Литература

1. Лорд Э.Э., Маккей А.Л., Ранганатан С. Новая геометрия для новых материалов. - М.: ФИЗМАТЛИТ, - 264 с.
2. Стюарт Я. Концепции современной математики. – Мн: Выш. школа, – 384с.
3. Иванов В.В., Таланов В.М. Разбиение и структурирование пространства, описание процесса формирования модульного кристалла // Успехи соврем. естествознания, - №8. – С.75-77.
4. Иванов В.В., Таланов В.М. Разбиение структурированного 3D пространства на модулярные ячейки и моделирование невырожденных модулярных структур // Успехи соврем. естествознания, - №10. – С.78-80.
5. Иванов В.В., Таланов В.М. Формирование структурного модуля для модулярного дизайна в 3D пространстве // Успехи соврем. естествознания, 2012. - №9. – С.74-77.
6. Иванов В.В., Таланов В.М. Принципы модулярного строения регулярных фрактальных структур // Успехи соврем. естествознания, - №3. – С.56-57.
7. Иванов В.В., Демьян В.В., Таланов В.М. Эволюционная модель формирования и анализ детерминистических фрактальных структур // Успехи соврем. естествознания, 2012. - №4. – С.230-232.
8. Иванов В.В., Таланов В.М., Гусаров В.В. Информация и структура в наномире: модулярный дизайн двумерных наноструктур и фрактальных решеток // Наносистемы: Физика, Химия, Математика, - Т.2. - № 3. - С.121-134.
9. Иванов В.В. Формирование и символьное описание детерминистических гибридных фрактальных структур в 2D пространстве // Современные наукоемкие технологии. - №.9 – С.89-93.
10. Иванов В.В., Таланов В.М. Конструирование фрактальных наноструктур на основе сеток Кеплера-Шубникова // Кристаллография, – Т.58. - № 3. - С. 370–379.
11. Иванов В.В. Комбинаторное моделирование вероятных структур неорганических веществ. – Ростов-на-Дону: Изд-во СКНЦ ВШ, 2003. – 204с.
12. Иванов В.В., Таланов В.М. Принцип модулярного строения кристаллов // Кристаллография, - Т.55. - № 3. - С.385-398.
13. Иванов В.В., Таланов В.М. Алгоритм выбора структурного модуля и модулярный дизайн кристаллов // Журн. неорганической химии, 2010. - Т.55. - № - С.980-990.
14. Иванов В.В., Таланов В.М. Комбинаторный модулярный дизайн структур шпинелеподобных фаз // Физика и химия стекла, - Т.34. - №4. - С.528-567.
15. Иванов В.В., Шабельская Н.П., Таланов В.М., Попов В.П. Итерационный модулярный дизайн двумерных наноструктур // Успехи соврем. естествознания, 2012. - №2. – С.60-63.
16. Иванов В.В., Шабельская Н.П., Таланов В.М. Информация и структура в наномире: модулярный дизайн двумерных полигонных и полиэдрических наноструктур // Соврем. наукоемкие технологии, 2010. - №10. - С.176-179.
17. Иванов В.В. Общая характеристика возможных гибридных мономодулярных фрактальных структур// Соврем. наукоемкие технологии. 2013.- №.5. – С.29-31.
18. Иванов В.В. Формирование фрактальных структур на основе итерационной последовательности и канторова множества точек с заданными характеристиками в 1D пространстве // Успехи соврем. естествознания, 2013. - №8. – С.136-137.
19. Иванов В.В. Описание и классификация точечных мономодулярных фрактальных структур // Успехи соврем. естествознания, - №8. – С.134-135.
20. Иванов В.В. Анализ возможности получения новых точечных и квазиточечных фрактальных структур на основе итерационной последовательности и канторова множества точек // Успехи соврем. естествознания, - №8. – С.129-130.
21. Иванов В.В., Демьян В.В., Таланов В.М. Информация и структура в наномире: модулярный дизайн фрактальных структур в двумерном пространстве // Междунар. журн. эксп. образования, - №11. - С.153-155.
22. Иванов В.В., Таланов В.М. Модулярное строение наноструктур: Информационные коды и комбинаторный дизайн // Наносистемы: Физика, Химия, Математика, 2010. - Т.1. - №1. - С.72-107.
23. Иванов В.В., Таланов В.М., Гусаров В.В. Символьное описание структурных типов кристаллов // Наносистемы: Физика, Химия, Математика, 2012. - Т.3. - № - С.82-100.
24. Иванов В.В., Таланов В.М. Символьное описание упаковок модулей и коды структур кристаллов / Журн. структурной химии, - Т.54. - №2. - С.354-376.