SYNTHESIS METHODS OF ALGORITHMS FOR CALCULATING COORDINATES STATE AND PARAMETERS OF COMPLEX DYNAMIC OBJECTS ON THE BASIS OF FULL ORDER OBSERVER

Вдовин В.В.

Аспирант, Новосибирский государственный технический университет

МЕТОДИКА СИНТЕЗА АЛГОРИТМОВ ВЫЧИСЛЕНИЯ КООРДИНАТ СОСТОЯНИЯ И ПАРАМЕТРОВ СЛОЖНЫХ ДИНАМИЧЕСКИХ ОБЪЕКТОВ НА ОСНОВЕ НАБЛЮДАТЕЛЕЙ ПОЛНОГО ПОРЯДКА

Аннотация

В статье обсуждается методика синтеза алгоритмов наблюдения неизмеряемых координат состояния и оперативной идентификации изменяющихся параметров сложных динамических объектов, базирующаяся на структуре адаптивного наблюдателя полного порядка, а также ее применение в задачах бездатчикового векторного управления асинхронными электроприводами.

Ключевые слова: наблюдение, идентификация, синтез, адаптивный наблюдатель полного порядка.

Vdovin V.V.

Postgraduate student, Novosibirsk State Technical University

SYNTHESIS METHODS OF ALGORITHMS FOR CALCULATING COORDINATES STATE AND PARAMETERS OF COMPLEX DYNAMIC OBJECTS ON THE BASIS OF FULL ORDER OBSERVER

Abstract

The article discusses synthesis method of observation algorithm of  unmeasured coordinates state  and  the rapid identification of changing parameters of complex dynamic objects, based on the structure of adaptive full-order observer, and it also discusses its application in the problems of sensorless vector control of asynchronous electric drives.

Keywords: observing, identification, synthesis, adaptive full order observer.

Постановка задачи

Для обеспечения высокого качества технологического процесса и экономической эффективности производства к системам регулирования предъявляются все более высокие требования к статическим и динамическим показателям и одновременной простоте, надежности и невысокой стоимости. Именно по этой причине все чаще применяются замкнутые систем автоматического управления (САУ). Применительно к электроприводу – применение замкнутых систем регулирования частоты вращения вала двигателя. Для построения замкнутых систем необходима достоверная текущая информация о координатах системы. Однако использование датчиков для получения информации обо всех координатах состояния объекта управления необходимых для построения замкнутых САУ не всегда целесообразно и возможно. Например, для построения системы векторного управления машинами переменного тока необходима информация об опорном векторе потокосцепления, измерение которого датчиками холла затруднительно.

Кроме того, параметры объекта управления в процессе работы могут изменяться в широких пределах, что может потребовать использования адаптивных систем управления, для функционирования которых необходима информация об изменяющихся параметрах.

Следовательно, часто перед разработчиками САУ встает проблема наблюдения неизмеряемых координат состояния и идентификации параметров объекта управления в текущий момент времени. Для исключения двояких толкований в терминах «наблюдения» и «идентификации» в данной работе используется понятие «вычисления», под которым понимается восстановление информации о неизмеряемых координатах состояния или параметрах объекта по информации о доступных измерению координатах состояния. Таким образом, необходимы специальные алгоритмы вычисления координат и параметров.

В настоящее время существует большое количество алгоритмов  вычисления координат и параметров объектов управления. Их можно условно разделить на активные и пассивные. Под активными алгоритмами понимаются алгоритмы текущей алгоритмы используют в своей работе различные тестовые воздействия, которые влияют на координаты состояния и, соответственно, должны быть достаточно «малы» для того чтобы не влиять на ход технологического процесса, что в свою очередь требует использования высокоточных средств измерения для выявления реакции объекта управления. Пассивные алгоритмы используют лишь «рабочие»  сигналы координат состояния. Наилучшие результаты в данном классе методов показывают адаптивные алгоритмы вычисления координат и параметров. Данные системы используют эталонную и настраиваемую модель. В качестве эталонной модели может служить как математическая модель объекта (например, алгоритмы MRAS [1] для асинхронных двигателей) так и сам объект управления. В качестве настраиваемой модели используется математическая модель объекта, которая должна быть известна. Для построения таких алгоритмов используется метод функций Ляпунова [2].

Однако рядом авторов [3,4,5] при синтезе алгоритмов вычисления для машин переменного тока допускаются типовые ошибки, приводящие к наличию областей неработоспособности предлагаемых ими алгоритмов в области малых частот питания и генераторных режимах работы. Предлагаемые в работе [5] алгоритмы, позволяющие исправить эту ситуацию, теоретически не обоснованы и вызывают ряд вопросов по выбору числовых коэффициентов предлагаемых алгоритмических «костылей».

Ниже предложена методика синтеза алгоритмов вычисления координат состояния и параметров объекта, основанная на использовании адаптивной системы, использующей в качестве настраиваемой модели наблюдатель полного порядка. Методика получена в результате исследования и синтеза алгоритмов вычисления для машин переменного тока.

Синтез структуры алгоритма вычисления координат состояния и параметров объекта

Необходимо представить математическую модель объекта в виде:

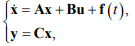                                                                                  (1)

где 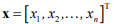 – n-мерный вектор координат состояния;

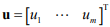 – m-мерный вектор измеряемых управляющих воздействий;

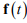 – вектор независимых возмущений, информация о которых доступна;

y  – k-мерный вектор выходных переменных (координат состояния доступных для прямых измерений);

A  – собственная матрица объекта,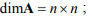 

B  – матрица управления;

C – матрица выхода,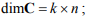 

Собственная матрица объекта А зависит от изменяемых во времени параметров объекта , которые должны в ходить в нее линейно. Матрица B должна не зависеть от изменяющихся параметров.

В качестве настраиваемой модели принимается модель наблюдателя полного порядка

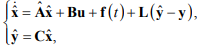                                                (2)

где ^ – знак оценки соответствующей величины;

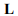 – искомая матрица стабилизирующей добавки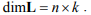 

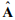 – собственная матрица наблюдателя, оперирующая оценками неизмеряемых параметров объекта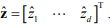

Вычитая из уравнений наблюдателя (2) уравнения объекта получим модель динамики ошибок наблюдения координат состояния

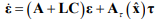
где 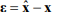 – вектор ошибок наблюдения координат состояния;

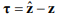 – d-мерный вектор отклонений параметров;

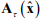 – матрица влияния отклонения параметров на ошибку наблюдения координат состояния зависящая от оценок координат.

Таким образом, отклонения параметров влияют на ошибки наблюдения координат.

Информация об отклонениях параметров должна восстанавливаться по информации об ошибках наблюдения координат

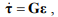                                                                                       (3)

где G– искомая матрица адаптации,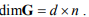 

Соответственно модель динамики ошибок наблюдения координат и параметров объекта имеет вид

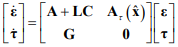                                                     (4)

       Так как адаптивные системы являются нелинейными для их синтеза необходимо применять метод функции Ляпунова [6]. В качестве метода построения функции Ляпунова предлагается использовать метод Красовского. Согласно этому методу функция Ляпунова задается в виде

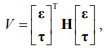
где Н – искомая симметричная квадратная матрица весовых коэффициентов,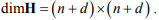

Матрицу весовых коэффициентов рекомендуется выбрать в виде

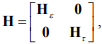                                                                           (5)

где 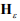 – искомая симметричная квадратная матрица весовых коэффициентов ошибок наблюдения координат, ;

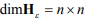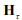 – искомая симметричная квадратная матрица весовых коэффициентов отклонений параметров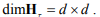

Нулевая побочная диагональ матрицы Н обеспечивает при синтезе «развязку» ошибок наблюдения координат и отклонений параметров друг от друга.

Функция Ляпунова должна быть положительно определенной, а так как она является квадратичной формой, то для ее положительной определенности, согласно критерию Сильвестра [6], необходимо и достаточно, чтобы квадратная матрица весовых коэффициентов  была положительно определенной.

Производная функции Ляпунова

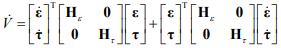
При подстановке модели динамики ошибок (4) в производную функции Ляпунова имеем

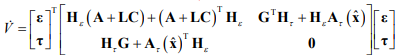
Для обеспечения отрицательной определенности производной функции Ляпунова (выполнение критерия Сильвестра) необходимо чтобы:

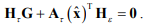
Соответственно матрица адаптации должна определяться согласно выражению

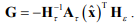
При этом из производной функции Ляпунова будут исключены отклонения параметров

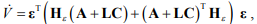
Производная функции Ляпунова должна быть отрицательно определенной функцией, соответственно квадратная матрица 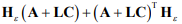 должна быть отрицательно определенной.

Законы вычисления отклонения параметров

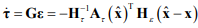                                                (6)

Тогда законы адаптации параметров

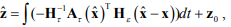
где 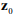 – априорные оценки параметров (получаемые в результате предварительной идентификации).

Следовательно, законы адаптации параметров в общем виде зависят от оценок координат состояния и самих координат. Однако для работы алгоритма доступны только выходные переменные .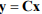

Таким образом, весовые коэффициенты и матрица «стабилизирующей» добавки должны одновременно обеспечить выполнение трех условий:

       1. Вхождение в закон вычисления оценок (6) только выходных переменных доступных для прямых измерений .

       2. Отрицательную определенность квадратной матрицы:

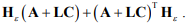
       3. Положительная определенность матрицы весовых коэффициентов H.

Синтез параметров алгоритма вычисления координат и параметров

Для обеспечения этих трех условий должна быть выбрана матрица стабилизирующей добавки и весовые коэффициенты либо соотношения между ними. Эта задача является достаточно сложной и может иметь не одно решение. Автором рекомендуется следующий порядок действий:

       1. Следует задаваться наибольшим количеством элементов матрицы 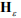 – не ограничиваться лишь коэффициентами по главной диагонали.

       2. Матрицу 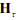 рекомендуется выбирать строго диагональной – для исключения связи между отклонениями параметров. Однако допускается применение недиагональных элементов.

    3. В общем виде найти законы вычисления оценок и исключить из них неизменяемые переменные путем выбора соотношений между весовыми коэффициентами. При этом могут быть получены соотношения только между несколькими весовыми коэффициентами.

     3. При принятых соотношениях коэффициентов проверить положительную определенность матрицы H либо наложить условия на соотношения между другими коэффициентами.

       4. Проанализировать матрицу

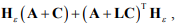
при L= 0 с учетом принятых соотношений между весовыми коэффициентами.

В случае если она отрицательно не определена, выбрать матрицу «стабилизирующей» добавки и при необходимости соотношения еще не определенных коэффициентов так чтобы обеспечить отрицательную определенность матрицы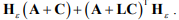

       5. В матрицу стабилизирующей добавки могут войти изменяющиеся параметры объекта L(z). В этом случае необходимо перейти к их оценкам, исходя из допущения .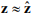

       6. В результате все весовые коэффициенты должны быть связаны между собой некоторыми соотношениями либо четко определены. Должна быть получена матрица «стабилизирующей» добавки

       7. Полученные в ходе синтеза законы адаптации являются в общем виде интегральными.

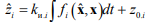
       В некоторых случаях они могут быть дополнены пропорциональной частью

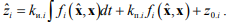
   8. Если весовые коэффициенты не определены, а определены лишь соотношения между ними, то для получения коэффициентов законов адаптации может быть использован метод линеаризации уравнений динамики объекта с учетом законов адаптации, либо метод проб и ошибок. В общем случае коэффициенты законов адаптации могут завесить от самих параметров объекта.

       Общая структурная схема алгоритма идентификации координат состояния и неизменяемых параметров представлена на рис. 1.

       9. Результаты должны быть проверены методом численного моделирования.

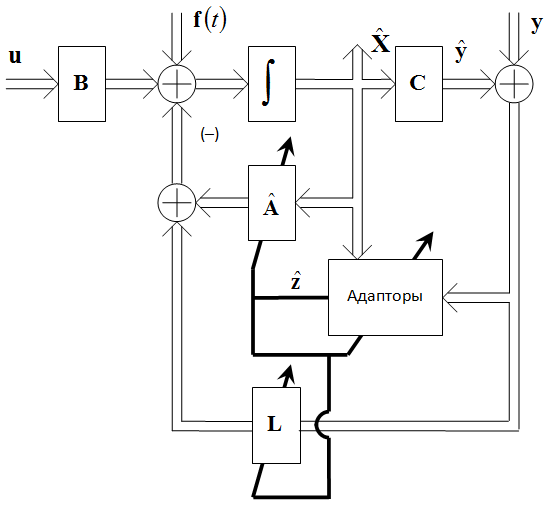
Рис. 1 – Структурная схема алгоритма вычисления координат и параметров

Согласно предлагаемой методике были синтезированы алгоритмы вычисления для асинхронного двигателя с короткозамкнутым (АДКЗР) [7] и фазным ротором [8], а также синхронного двигателя с магнитоэлектрическим возбуждением [9] предназначенные для работы в составе систем бездатчикового векторного управления. Использование методов линеаризации алгоритмов вычисления позволило рекомендовать конкретные методики расчета законов адаптации для этих систем. Ниже кратко приведены результаты синтеза для АДКЗР.

Алгоритм вычисления координат и параметров АДКЗР

Алгоритм вычисляет необходимую для построения системы векторного управления информацию об опорном векторе потокосцепления машины – потокосцеплении ротора, вычисляет оценку частоты вращения ротора двигателя необходимую для построения замкнутой САУ регулирования частоты вращения. Следует отметить, что частота вращения двигателя является координатой состояния для электропривода с учетом движения механической части, однако входит в математическую модель двигателя как изменяющийся параметр.

Математическая модель АДКЗР

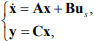
где 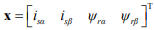 – вектор координат состояния объекта – токов и потокосцеплений,  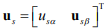– вектор  управляющих воздействий,  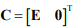– матрица выхода,  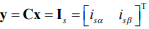– вектор-столбец доступных для прямого измерения переменных, А – собственная матрица АДКЗР,

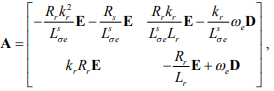
где 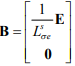 – матрица управления;

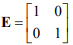 – единичная матрица;

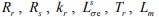 – неизменяемые параметры двигателя;

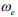– электрическая частота вращения ротора двигателя – изменяющийся параметр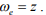

Собственная матрица наблюдателя 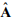будет иметь вид

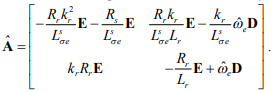
Соответствующая матрица влияния отклонения параметров на ошибку наблюдения координат состояния

.

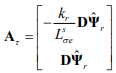Предлагается использовать матрицы весовых коэффициентов вида:

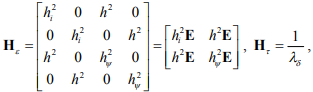
где 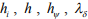 – некоторые положительные константы.

Закон адаптации частоты вращения:

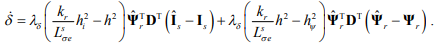
Для исключения, не измеряемого вектора потокосцепления ротора необходимо принять соотношение

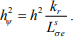                                                                                 (7)

При анализе положительной определенности матрицы H получим условие, накладываемое на соотношение весовых коэффициентов

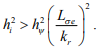                                                                          (8)

Для отрицательной определенности квадратичная матрица 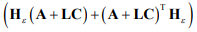 при принятом соотношении (7) можно принять соотношение

        

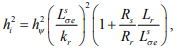
которое удовлетворяет условию (8).

И использовать матрицу стабилизирующей добавки

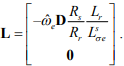
При принятых соотношениях закон адаптации электрической частоты вращения ротора

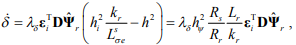
в который входят две неопределенные величины 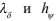, поэтому для получения численных значений коэффициентов адаптации необходимо использовать, например, подход, описанный в [7].

Дополняя (2.14) пропорциональной частью получим пропорционально-интегральный закон формирования оценки электрической частоты вращения двигателя:

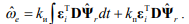
Стоить отметить, что весовые коэффициенты и соотношения между ними фигурируют только при синтезе закона адаптации и стабилизирующей добавки.

Результаты моделирования предлагаемого алгоритма подтверждают его работоспособность и устойчивость во всей плоскости механических характеристик.

Заключение

Предлагаемая методика синтеза алгоритма вычисления позволяет синтезировать структуру и численные значения коэффициентов законов адаптации и матрицы «стабилизирующей» добавки. Использование в качестве настраиваемой модели наблюдателя полного порядка обеспечивает отсутствие в структуре алгоритма «открытых» интеграторов.