SIMULATION OF BANDPASS FILTER

Иванов М.Л.

Аспирант, Томский политехнический университет

МОДЕЛИРОВАНИЕ ПОЛОСОВОГО ФИЛЬТРА

Аннотация

Приведены результаты моделирования фильтров нижних и верхних частот в пакете Orcad. Рассмотрено влияние полосового фильтра Баттерворта четвертого порядка с нижней и верхней границей 0,05 Гц и 75 Гц соответственно на смесь синусоидальных сигналов с частотами 0,001 Гц, 5 Гц, 100 Гц в пакете Matlab.

Ключевые слова: фильтр, АЧХ, моделирование.

Ivanov M.L.

Postgraduate student, Tomsk Polytechnic University

SIMULATION OF BANDPASS FILTER

Abstract

Simulation results of low-pass filters and high frequencies are represented in the package Orcad. The effect of Butterworth bandpass filter of the fourth order with the lower and upper boundary of 0.05 Hz and 75 Hz, respectively, are investigated on a mix of sine waves with frequencies of 0,001 Hz, 5 Hz, 100 Hz in the package Matlab .

Keywords: filter, amplitude-frequency characteristics, simulation  

В настоящее время в современной медицине используются различные средства для определения диагноза пациента. Одним из таких средств является электрокардиограф, при помощи которого производится регистрация электрических полей, образующихся при работе сердца. Снятие ЭКГ-сигнала происходит посредством электродов, прикрепленных к телу пациента, и дальнейшим записыванием его во внутренний носитель информации. Перед этапом сохранения сигнал проходит через электрические фильтры, встроенные в электрокардиограф. Они осуществляют фильтрацию шума, но также искажают и полезную информацию. Для исследования влияния фильтров на ЭКГ-сигнал, необходимо неотфильтрованный сигнал пропустить через различные типы фильтров и провести анализ полученной кривой.

Фильтры могут быть классифицированы по ряду признаков:

1) по виду АЧХ они разделяются на: фильтры нижних частот (ФНЧ, рисунок 1,а); фильтры верхних частот (ФВЧ, рисунок 1,б); полосовые фильтры (ПФ, рисунок 1,в); режекторные (заграждающие) фильтры (РЖ, рисунок 1,г);

2) в зависимости от полиномов, используемых при аппроксимации передаточной функции, различают фильтры: критического затухания, Бесселя, Баттерворта, Чебышева;

3) по элементной базе фильтры разделяются на пассивные и активные фильтры. Активные фильтры включают в схему RLC-фильтра активный элемент, в качестве которого часто используются операционные усилители [1].

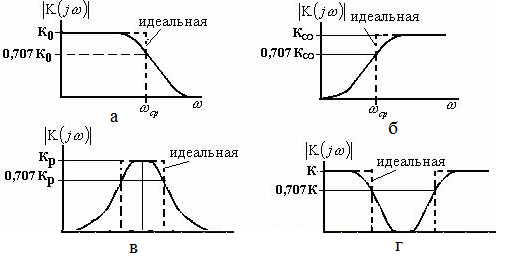
Рис. 1 –  Амплитудно-частотные характеристики различных фильтров

Различные виды АЧХ ФНЧ представлены на рисунке 2.

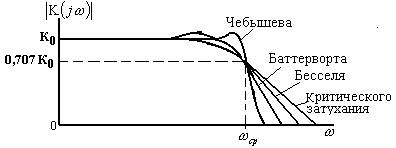
Рис. 2 – АЧХ различных фильтров нижних частот

АЧХ ФНЧ Баттерворта имеет довольно длинный горизонтальный участок и резко спадает за частотой среза. Переходная характеристика такого фильтра имеет колебательный характер. С увеличением порядка фильтра колебания усиливаются.

Характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она имеет волнообразный характер с постоянной амплитудой. Колебания переходного процесса сильнее, чем у фильтра Баттерворта.

Фильтр Бесселя характеризуется меньшей длиной горизонтального участка, чем фильтр Баттерворта, и более пологим спадом АЧХ за частотой среза, чем фильтры Баттерворта и Чебышева.

Моделирование фильтров с заданными параметрами заключается в исследовании электрической схемы и определении влияния RC-элементов на АЧХ. Активный фильтр представляет собой схему из RC-элементов и операционного усилителя (рисунок 3).

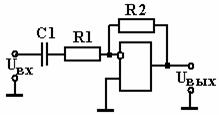
Рис. 3 – Пример схемы активного ФВЧ первого порядка

Так как фильтр, представленный выше, имеет первый порядок, то расчет RC-элементов не вызывает затруднений. В медицинской технике используются фильтры больших порядков, потому что АЧХ таких фильтров имеют лучшие характеристики. С повышением порядка фильтра расчет RC-элементов усложняется, поэтому целесообразно использовать программные пакеты, которые позволяют упростить процесс моделирования. Например, в программном пакете Orcad составляется электрическая схема из элементов, номиналы которых будут подбираться в процессе моделирования для получения требуемой характеристики фильтра.

Моделирование фильтров в Orcad производится по стандартным схемам, где реализация активного фильтра достигается за счет добавления в схему операционного усилителя. На рисунке 4 приведена схема активного фильтра высоких частот второго порядка с частотой среза 2 Гц, АЧХ данного фильтра представлена на рисунке 5. На этом рисунке видно плавную кривую с небольшим изменением коэффициента передачи, следовательно, амплитуда сигнала, проходящая через фильтр, будет искажаться незначительно в полосе пропускания.

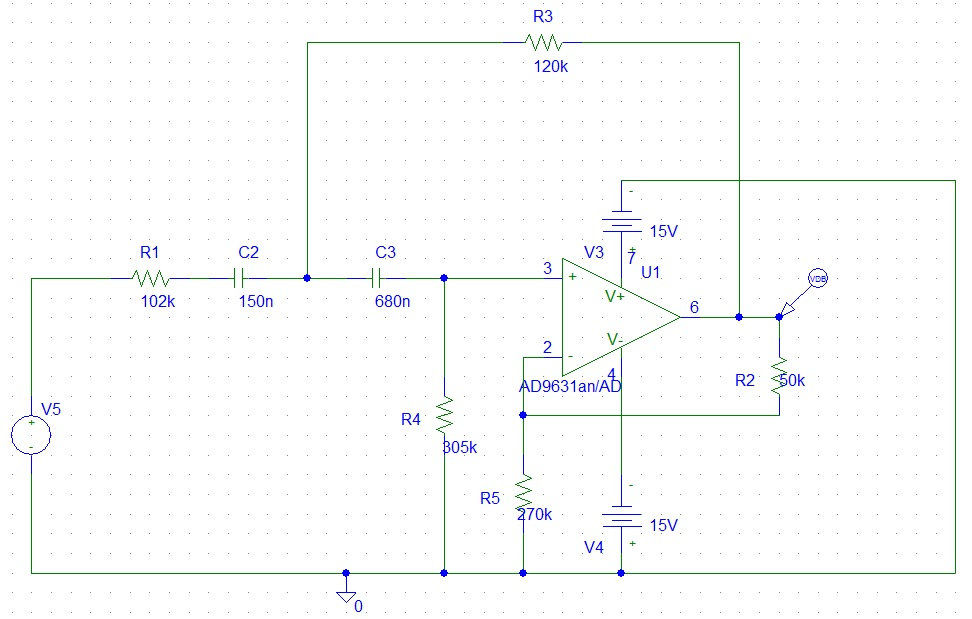
Рис. 4 – Схема активного ФВЧ второго порядка

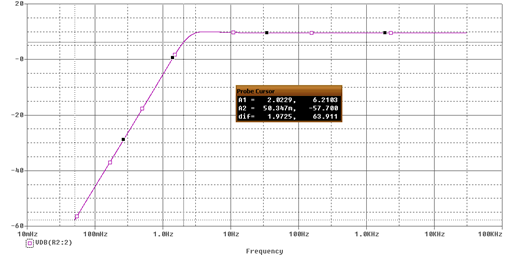
Рис. 5 – АЧХ активного ФВЧ второго порядка

В электрокардиографе кроме ФВЧ присутствует ФНЧ, вместе эти два фильтра образуют полосовой фильтр. Схема ФНЧ представлена на рисунке 6, на которой видно, что расположение RC элементов изменилось относительно схемы ФВЧ. Кроме расположения элементов так же изменились их значения, которые были рассчитаны для получения частоты среза 75 Гц. АЧХ фильтра низких частот второго порядка представлена на рисунке рисунок 7. На графике видно небольшое изменение коэффициента передачи в полосе пропускания, что внесет искажение во входной сигнал в этой полосе.

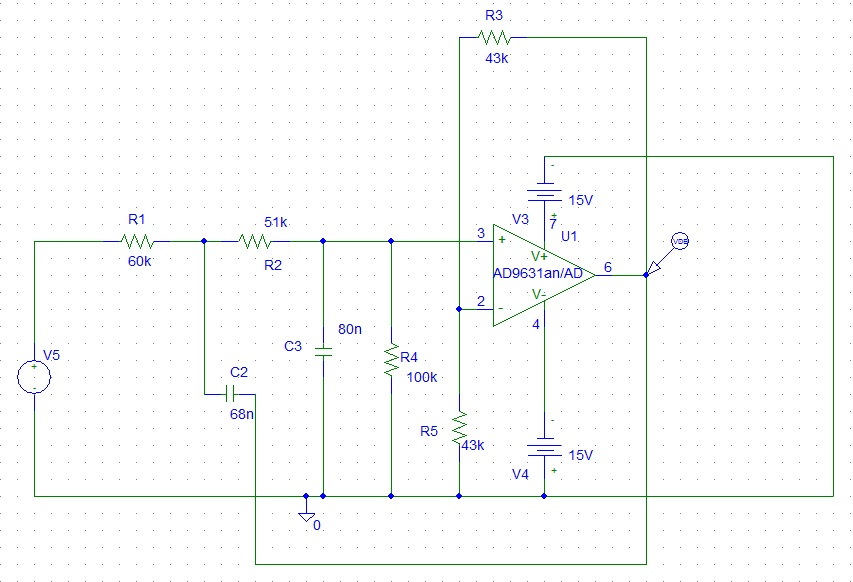
Рис. 6 – Схема активного ФНЧ второго порядка

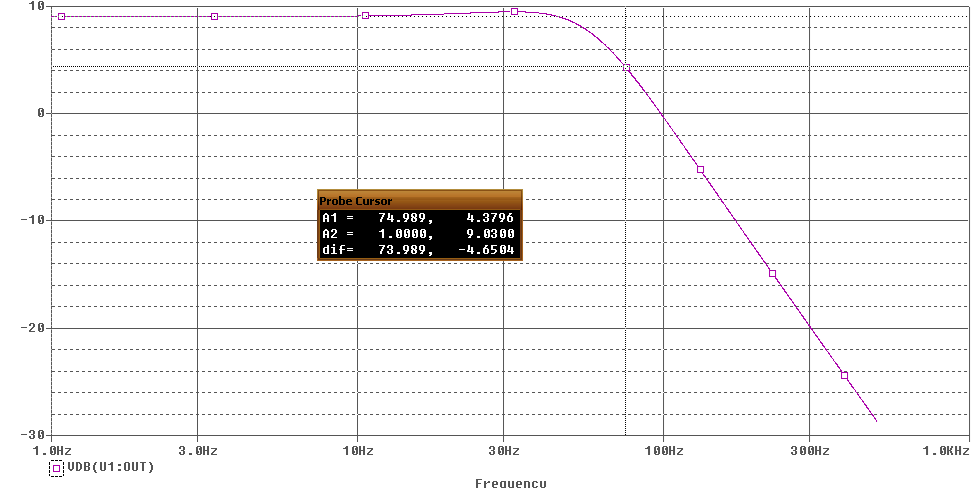
Рис. 7 – АЧХ активного ФНЧ второго порядка

АЧХ смоделированных фильтров описывает кривую похожую на фильтр Чебышева: обладает крутым спадом, но в полосе пропускания есть изменение коэффициента передачи. Для более полного исследования влияния фильтров на сигнал следует смоделировать несколько типов фильтров, увеличивать их порядок, изменять полосу пропускания. Так как в Orcad это займет немало времени, то будет целесообразно использовать программу, которая позволить упростить моделирование фильтров. Одной из таких программ является Matlab, где получение передаточной функции звена фильтра сводится к использованию встроенных команд с заданием параметров.

Для моделирования фильтров, например, полосового, состоящего из ФВЧ и ФНЧ, в программе Matlab существует несколько команд, последовательное применение которых позволяет получить желаемую передаточную функцию фильтра. После её получения составляется структурная схема со звеньями, генератором синусоидальных сигналов и осциллографа. Для определения влияния фильтров на сигнал требуется сравнить входной и выходной сигналы.

Моделирование фильтров происходит в несколько этапов, в каждом из которых требуется выполнение определенных действий: выбор типа фильтра, подбор параметров для вычисления передаточной функции звена фильтра и построение структурной схемы [2]. Пусть требуется смоделировать ПФ Баттерворта 4-го порядка с нижней и верхней границей 0.05 Гц и 75 Гц соответственно. Для того чтоб получить ПФ, сначала моделируется ФВЧ и ФНЧ, а потом они устанавливаются в схему последовательно. Расчет передаточных функций для звеньев ФВЧ и ФНЧ производится функциями:

1. [n, Wn] = buttord (Wp, Ws, Rp, Rs, 's');
2. [b,a]=butter(n, Rp, Wn, 's').

АЧХ схемы (рисунок 8), которая состоит ПФ 4-го порядка Баттерворта и режекторного фильтра 50 Гц, представлена на рисунке 9.

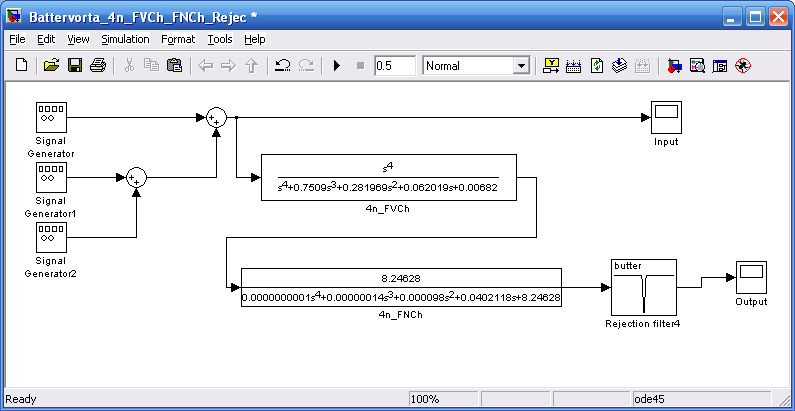
Рис. 8 – Структурная схема

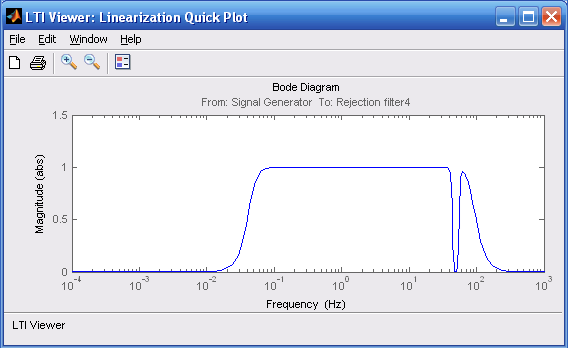
Рис. 9 – АЧХ ПФ и режекторного 4-го порядка

В процессе исследования на вход фильтров подается смесь синусоидальных сигналов с частотами 0.001 Гц, 5 Гц, 100 Гц, который проходит через фильтры и отображается на осциллографе, для удобства сравнения также отображается сигнал, поступающий на вход фильтров. Из сравнения входного и выходного сигналов (рисунок 10, рисунок 11) видно уменьшение  высокочастотных пиков.

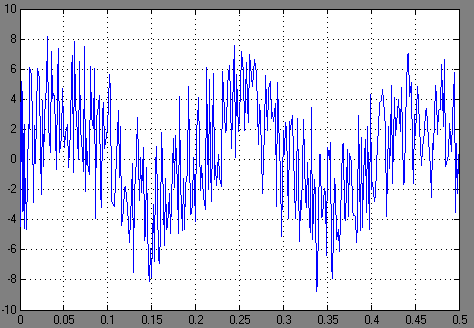
Рис. 10 – Сигнал на входе фильтров

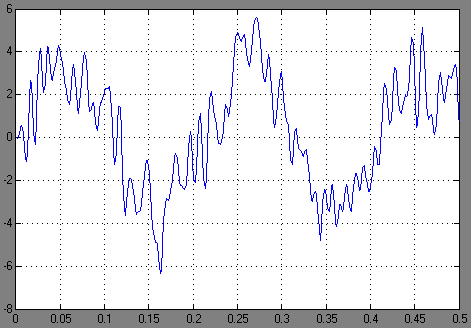
Рис. 11 – Выходной сигнал

Сигнал с частотой 5 Гц претерпел наименьшие изменения, так как находится в полосе пропускания полосового фильтра. Если брать во внимание ЭКГ-сигнал, то влияние на него может по-разному сказаться на результате, либо он поможет определить диагноз пациента, убрав шум из сигнала, либо исказить полезный. Поэтому следует тщательно подходить к вопросу о выборе типа и порядка фильтра для достижения поставленной цели.