OPTIMUM MANAGEMENTS OF ENTERPRISE PROFIT WITH USE OF PRODUCTION LEVERAGES

Люкманов В.Б.¹, Мандыч И.А.², Скрябина О.С.³

¹Доцент, кандидат технических наук; ²доцент, кандидат экономических наук; ³студент; Московский Государственный университет Тонких Химических технологий имени М.В.Ломоносова

ОПТИМАЛЬНОЕ УПРАВЛЕНИЯ  ПРИБЫЛЬЮ ПРЕДПРИЯТИЯ С ИСПОЛЬЗОВАНИЕМ ПРОИЗВОДСТВЕННЫХ ЛЕВЕРИДЖЕЙ

Аннотация

В данной статье рассмотрено влияние скорости изменения взаимосвязанных экономических показателей, с использованием «чистых» и «натуральных» левериджей. Разработана оптимизационная модель позволяющая определить оптимальный объем выпуска продукции с учетом известных зависимостей между выпуском, ценой и затратами на производство, которые выражаются уравнениями зависимостей и соответствующими уровнями левериджей.

Ключевые слова: леверидж, «чистый» леверидж, «натуральный» леверидж.

lyukmanov V.B.¹, Mandych I.A.², Skryabina О.S.³

¹Assosiate professor, Ph.D.; ²assosiate professor, Cand.Econ.Sci.; ³student; Lomonosov Moscow State University of Fine Chemical Technologies.

OPTIMUM MANAGEMENTS OF ENTERPRISE PROFIT WITH USE OF PRODUCTION LEVERAGES

Abstract

In this article considers the influence of the rate of change of the interconnected economic indicators, with use of "pure" and "natural" leverages. The optimizing model allowing to determine the optimum volume of output taking into account known dependences between release, the price and costs of production which are expressed by the equations of dependences and appropriate levels of leverages is developed.

Keywords: leverage, "pure" leverages, "natural" leverages.

Понятие «леверидж» в теории финансов связано с различной скоростью изменения взаимосвязанных экономических показателей, когда изменение одного из них вызывает большее или меньшее изменение другого [1]. Например, изменение объема выпуска продукции или цены на нее или затрат вызывает  больший или меньший темп роста прибыли.

Исходя из формулы прибыли:  P=Q·(p-v) – C, где Pr – прибыль, Q - объем выпуска продукции,  p- цена, v – переменные затраты,  C – постоянные затраты,  можно говорить о 4-х левериджах:

Натуральный леверидж: его сила L_Q= (Pr+C)/Pr  или  = Q·(p-v)/Pr  показывает, во сколько быстрее вырастит прибыль по сравнению с ростом объема выпуска (если все остальные показатели не изменяются).

Ценовой леверидж: его сила L_p=Q·p/Pr показывает, во сколько быстрее вырастит прибыль по сравнению с ростом цены (если  все остальные показатели не изменяются). Эту формулу легко понять: изменение цены увеличивает или уменьшает одновременно и выручку и прибыль на одну и туже величину – на Q·∆p, но процент изменения и того и другого будет разный. Вот вывод формулы ценового левериджа:

L_p = (Q·∆p/Pr) : (Q·∆p/Qp) =  Q·p/Pr

Леверидж переменных затрат: его сила определяется аналогично: L_v = - Qv/Pr  показывает, во сколько быстрее вырастает прибыль по сравнению с переменными затратами (если  все остальные показатели не изменяются).

L_v = - (Q·∆v/ Pr) : (Q·∆v/Qv) = - Q·v/Pr

Леверидж постоянных затрат: его сила определяется аналогично L_с = - С/Pr  показывает, во сколько быстрее вырастает прибыль по сравнению с постоянными затратами (если  все остальные показатели не изменяются). L_c = - (Q·∆С/Pr)  :  (Q·∆С/C) =  - C/Pr

Все левериджи связаны между собой и эти связи помогают  глубже понять их экономическую суть.

Натуральный леверидж  связан с левериджем постоянных затрат: L_Q=1-L_c. Это равенство показывает, что дополнительный прирост прибыли  связан с более эффективным использованием  постоянных затрат – они не растут при увеличении объема выпуска продукции.

Ценовой леверидж  связан с левериджами и переменных и постоянных затрат:

L_p = 1 - L_c - L_v

Это равенство показывает, что возможность реализации продукции по более высокой цене повышает эффективность использования и постоянных и переменных затрат, именно за счет этого прибыль растет еще быстрее.

Это же равенство показывает, что левериджи переменных и прибыли постоянных затрат и имеют обратную зависимость: при неизменной цене и прибыли структура затрат определяет каждый из этих левериджей и соответственно силу их влияния на прибыль.

Но левериджи постоянных и переменных затрат могут являться не только  вспомогательными для понимания процессов получения дополнительной прибыли при увеличении выпуска продукции и цены, но и могут играть самостоятельную роль при формировании прибыли: они могут быть самостоятельным фактором роста прибыли.

Левериджи ценовой, переменных и постоянных затрат являются чистыми левериджами, т.е. в такой записи работают только в случае, если объем производства при этом не меняется, а меняются только рыночные условия реализации продукции, или только повышается качество продукции, или только проводятся мероприятия по снижению переменных и/или постоянных затрат без изменения объема производства и т.п. Эти 3 левериджа работают независимо друг от друга.

Но если меняется выпуск продукции и работает натуральный леверидж, то это обстоятельство меняет силу всех остальных левериджей:

L_p’= L_p·I_Q/I_pr

L_v^’ =  L_v·I_Q/I_Pr

L_c^’= L_c/I_pr   

где  I_Q= 1+∆Q (в долях единицы),  I_pr = 1+L_q·∆Q  - индексы изменения объема выпуска продукции и прибыли.

Эти новые левериджи применяются для новых уровней Q и Pr.

В теории индексов так же, как правило, сначала определяется влияние количественного фактора, а затем качественных. Часто это логически объяснимо: рост объема выпуска и продаж вызывает необходимость снизить цену, чтобы реализовать большее количество продукции; снижает переменные затраты в связи с приобретением большего опыта производства; увеличивает постоянные затраты (дополнительное оборудование, управление, склады, экологические мероприятия и т.п.).  И наоборот, снижение затрат позволяет снизить цену на конкурентном рынке и реализовать больше   продукции.

Прогноз роста прибыли за счет изменения качественных факторов равен:

∆Pr’’ = Pr’· (L_p·∆p + L_v·∆v + L_c·∆C)

Можно рассчитать прогнозное значение изменения прибыли более просто по одной общей формуле с использованием чистых левериджей и исходных данных:

∆Pr = Pr · (L_Q·∆Q + L_p·I_Q·∆p + L_v·I_Q·∆v + L_c·∆C)

Задача управления прибылью предприятия может заключаться в определении оптимального объема выпуска продукции с учетом известных зависимостей между выпуском, ценой и затратами на производство, которые выражаются уравнениями зависимостей и соответствующими уровнями левериджей.

В примере известны базовые значения выпуска продукции, цены, переменных и постоянных затрат: Q=100 млн. ед.,  p=20 руб./ед.,   v=10 руб./ед.,   C=600 млн. руб.,     Pr=400 млн. руб.

Известны зависимости изменения основных показателей от изменения объема выпуска продукции:

∆p = -0,07 ∆Q – 0,25 ∆Q²;

∆v =   - 0,2 ∆Q;

∆C =  0,02 ∆Q.

Оптимизационная модель имеет вид:

Переменной является изменение объема выпуска продукции: ∆Q.

Целевая функция -  суммарное изменение прибыли: F = ∆Q∙ L_Q+ ∆p∙ L_p + ∆v∙ L_v +∆C∙ L_c

Ограничения:

∆p = -0,07 ∆Q – 0,25  ∆Q²;

∆v =   - 0,2 ∆Q

∆C =  0,02 ∆Q ,

L_p’= L_p∙I_Q/I_pr ,

L_v^’ =  L_v∙I_Q/I_Pr  

L_c^’= L_c/I_p.

На рисунке 1 представлена модель и результаты ее решения оптимизационным методом в программе  Excel.

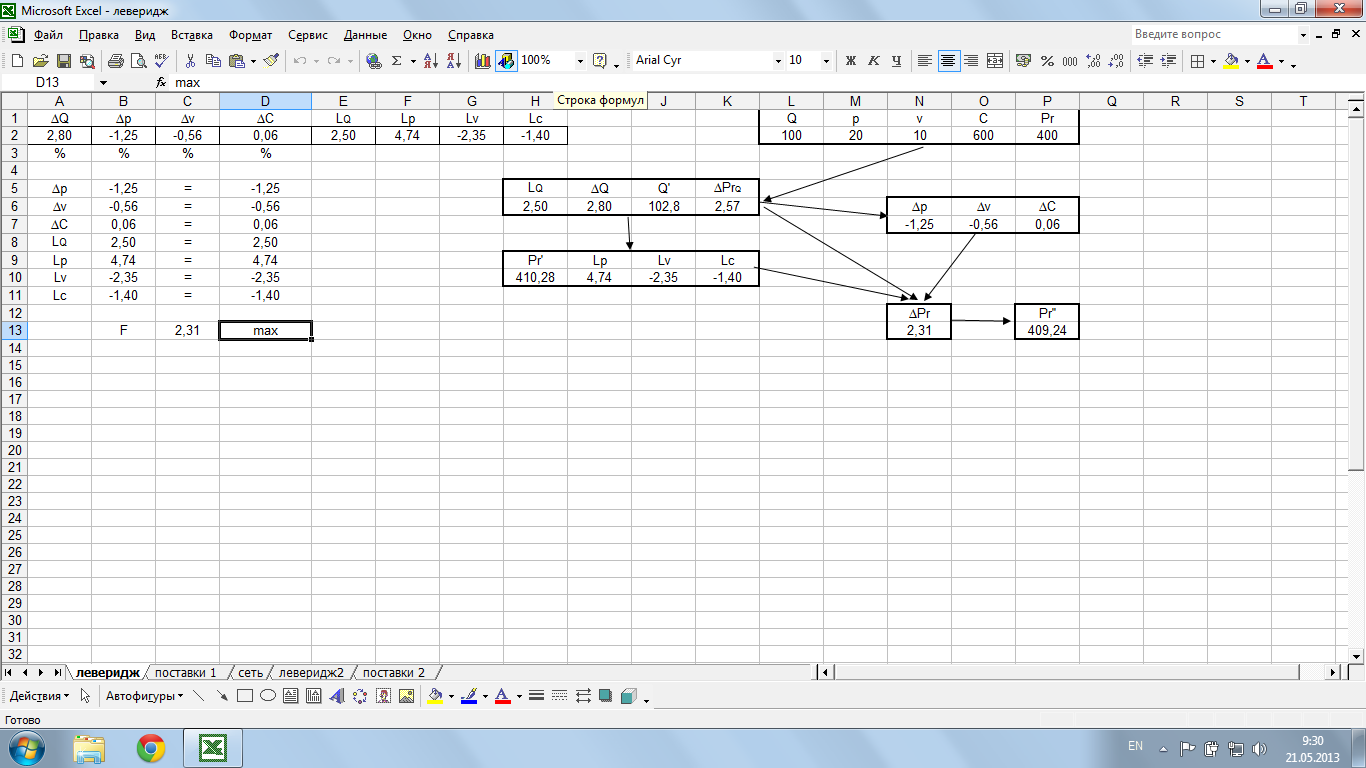
Рис.1 Расчет задачи управления прибылью предприятия оптимизационным методом.

Оптимально целесообразно увеличить объем производства на 2,8%, что дает суммарный максимальный прирост прибыли на 2,31%, которая увеличится на 9,24 млн.руб.

 В результате известны изменения всех показателей и их новые левериджи.