NEW LAWS AND MATHEMATICAL FORMULAS ON HYDRODYNAMICS
Белашов А.Н.
Автор более 60 изобретений, одной константы, двух физических величин и более 25 законов физики в области электротехники, электрических явлений,гидродинамики, механизма образования планет и Галактик нашей Вселенной.
E-mail: aleksey@belashov.info Сайт: http://www.belashov.info
НОВЫЕ ЗАКОНЫ И МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ ПО ГИДРОДИНАМИКЕ
Аннотация
Статья посвящена открытию новых законов гидродинамики определяющих момент силы, работу, энергию и период времени необходимый для перемещения одного исследуемого слоя водного потока или жидкой смеси проходящего по переменному сечению русла реки или трубопровода. По новым законам и математическим формулам гидродинамики, с учётом общих потерь в переменном сечении горизонтальной трубы или устье реки, можно определить момент силы, работу и энергиюжидкой смеси проходящей по переменному сечению реки или трубопровода. Эти законы нужны для того чтобы глубже разобраться в механизме перемещении жидкости по переменному сечению русла реки или трубопровода, где часто используют закон Бернулли, который являетсякак бы, следствием закона сохранения энергии. При этом необходимо отметить, что закон Даниила Бернулли не соответствует размерным единицам физических величин и не учитывает множество потерь при перемещении водного потока или жидкой смеси по переменному сечению трубопровода, и тем более, данный закон не может определить момент силы, работу или энергию водного потока перемещающегося по руслу реки.
Ключевые слова: формулы, гидродинамика.
Balashov A.N.
Author of more than 60 inventions, one constant, two physical quantities, and more than 25 of the laws of physics in the field of electrical engineering, electrical phenomena, fluid dynamics, the mechanism of the formation of planets and galaxies in our universe.E-mail: aleksey@belashov.infoWebsite: http://www.belashov.info
NEW LAWS AND MATHEMATICAL FORMULAS ON HYDRODYNAMICS
Abstract
The article is dedicated to the discovery of new laws of hydrodynamics defining moment of force, work, energy and time required to move one of the layer of water flow or liquid mixture flowing in the variable section of the river channel or pipe. According to the new laws of hydrodynamics and mathematical formulas, considering the total loss in the AC section or the horizontal tube, the mouth of the can to determine torque, work and energy of the liquid mixture passing through the variable section of the river or pipe. These laws are necessary in order to better understand the mechanism of movement of the fluid in the variable section of the river channel or pipeline, which often use Bernoulli's law, which is, as it were, a consequence of the law of conservation of energy. It should be noted that the law of Daniel Bernoulli does not meet the dimensional units of physical quantities and do not take into account a lot of losses in water flow or movement of the liquid mixture in the variable section of the pipeline, and even more so, the law can not determine the moment of force, work or energy of moving water flow the bed of the river.
Keywords: formula, hydrodinamics.
Гидродинамика - раздел гидравлики, в котором изучаются законы движения несжимаемой жидкости и её взаимодействие с неподвижными и подвижными поверхностями. С точки зрения механики, жидкостью называется вещество, у которого в равновесии отсутствуют касательные напряжения. Жидкость обладает свойствами течь и принимать форму сосуда, в который она наливается или принимать форму неподвижной или подвижной поверхности, через которую она проходит. Методами гидравлики можно исследовать также движение газов, если скорость этого движения значительно меньше скорости звука, так как при скорости движения газа, близкой к скорости звука или превышающей её, начинает играть заметную роль сжимаемость газа, где методы гидравлики уже неприменимы. Практические применения гидродинамики чрезвычайно разнообразны. Гидродинамикой пользуются при проектировании кораблей и самолётов, расчёте трубопроводов, насосов, гидротурбин и водосливных плотин, при исследовании морских течений и речных наносов, изучении фильтрации грунтовых вод и нефти в подземных месторождениях и так далее…
В потоках несжимаемых жидкостей обычно действуют разные течения и силы. Например, ламинарное или турбулентное течение, которое включает в себя силы давления, сопротивления, вязкости, тяжести и так далее… Соблюдение их пропорциональности означает полное гидродинамическое подобие. Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, при котором соблюдается пропорциональность лишь основных, главных сил.
Ламинарное течение жидкости по плоской поверхности, которое не огибает какие-либо препятствия и перемещается определёнными слоями, является более предсказуемым и прогнозируемым. Тогда как турбулентное течение жидкости, сопровождается интенсивным перемешиванием и беспорядочным движением молекул жидкости и газа, пульсациями скоростей и давлений. При турбулентном течении жидкости векторы скоростей имеют не только осевые, но и нормальные к оси русла составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объёмов жидкости. Этим и объясняются пульсации скоростей и давления. Турбулентность может возникать и при нарушении однородности какой-либо среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха и пены. Мгновенные параметры среды становятся хаотичными.
Моделирование турбулентности - одна из наиболее трудных и нерешённых проблем в гидродинамике и теоретической физике. Турбулентность всегда возникает при превышении некоторых критических параметров - скорости и размеров обтекаемого тела или уменьшения вязкости текучей среды. Она так же может возникать при сильно неравномерных граничных и начальных условиях на границе обтекаемого тела. Или, может исчезать при сильном ускорении потока на поверхности, при сильной стратификации среды. Поскольку турбулентность характеризуется случайным поведением мгновенных значений скорости, давления и температуры в данной точке жидкости или газе, то это означает, что при одних и тех же условиях детальная картина распределения этих величин в жидкости будет различной и практически никогда не повторяется. Поэтому, мгновенное распределение скорости в различных точках турбулентного потока обычно не представляет интереса, а важными являются усреднённые величины. Проблема описания гидродинамической турбулентности заключается, в частности, и в том, что пока не удаётся на основании только уравнений гидродинамики предсказать, когда именно должен начинаться турбулентный режим и что именно в нём должно происходить без экспериментальных данных. На мощных компьютерах удаётся моделировать только некоторые типы течений. В результате, нам приходится довольствоваться лишь феноменологическим и приближённым описанием.
При изобретении гидрофизического кавитационного теплового нагревателя и бесплотинной гидроэлектростанции были открыты новые законы и математические формулы по гидродинамике, которые я представляю для вашего рассмотрения.
1. Новый закон определения периода времени необходимого для перемещения одного исследуемого ламинарного слоя водного потока жидкости можно сформулировать так:
Период времени необходимый для перемещения одного исследуемого ламинарного слоя водного потока равен корню квадратному от произведениясуммы массы исследуемого слоя водного потока и массы слоя находящегося над исследуемым слоем водного потока на сумму высоты исследуемого слоя и высоты слоя находящегося над исследуемым слоем водного потока и обратно пропорциональна разнице сил всего водного потока и потерь сил на перемещение каждого слоя.
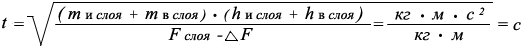
где:t - период времени необходимый для перемещения одного исследуемого ламинарного слояводного потока, с m в слоя - масса слоя находящегося над исследуемым слоем водного потока, м
h в слоя - высота слоя находящегося над исследуемым слоем водного потока, м
Δ F - потеря силы по перемещению каждого слоя водного потока, Н h и слоя - высота исследуемого слоя водного потока, м
m и слоя - масса исследуемого слоя водного потока, м
F - сила для перемещения всего водного потока, Н.
Нужно понять, что водный поток в русле реки перемещается с разным ускорением. Например, верхний слой водного потока будет течь быстрее, чем средний слой, а средний слой водного потока будет течь быстрее, чем нижний слой водного потока. Для подтверждения периода времени необходимого для перемещения одного исследуемого слоя водного потока жидкости, наглядно определим максимальную работу водного потока, который ламинарным потоком перемещается по руслу реки имеющего:
V - скорость водного потока русла реки = 1 м/с
L - длина водного потока русла реки = 1 м
a - ширина водного потока русла реки = 5 м
h - высота водного потока русла реки = 1 м.
Определим объём воды, которыйпротекает по руслу реки за 1 с:
V = (h · a) · L = (1 м · 5 м) · 1 м = 5 м ³
где:
V - объём воды, которыйпротекаетпо руслу реки, м ³
h - высота водного потока русла реки = 1 м
a - ширина водного потока русла реки = 5 м
L - длина водного потока русла реки = 1 м.
Из физики мы знаем, что плотность воды при 20°С, рв = 0,99823 г/см ³или998,23 кг/м ³.
Определим вес воды имеющего объём 5 м ³,который проходит за 1 с:
G = V · pв = 5 м ³ · 998,23 кг/м ³ = 4991,15 кг
где:
G - вес измеряемого объёма водного потока, кг
V - объём измеряемого объёма воды = 5 м ³
рв - плотность воды при 20 °С = 998,23 кг/м ³.
Переведём вес воды, который находится в 5 м ³ в Ньютоны:
9,80665 Н = 1 кг Х Н = 4991,15 кг
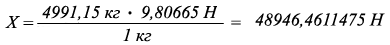
В Международной системе единиц принимается сила, которая телу массой 1 кг сообщает ускорение 1 м/с ².Такаяединица называется Ньютоном (Н).
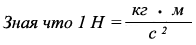
Определим работу водного потока находящегося в 5 м ³.
А = F · L = 48946,4611475 Н · 1 м = 48946,4611475 Н · м
где:
A - работа водного потока русла реки, Н · м
L - длина водного потока русла реки = 1 м
F - силаводного потока русла реки = 48946,4611475Н.
Из физики мы знаем, что мощностью называется работа производимая (или потребляемая) в одну секунду:
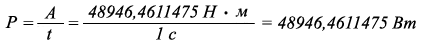
где:
P - мощность водного потока русла реки, Вт
A - работа водного потока русла реки = 48946,4611475 Н · м
t - время в течении которого производится данная работа = 1 с.
Переведём Вт в кВт:
1 кВт = 1000 Вт Х кВт = 48946,4611475 Вт
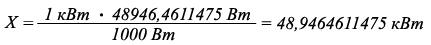
Необходимо подчеркнуть, что при проектировании бесплотинных гидроэлектростанций необходимо учитывать, что водный поток в русле рекиперемещается с разным ускорением. Например, верхний слой водного потока будет течь быстрее, чем средний слой, а средний слой водного потока будет течь быстрее, чем нижний слой водного потока.
Например,разделимвысоту водного потока русла реки на три равные части и определим массу каждого слоя, который проходит за 1 с:
где:
V - скорость водного потока русла реки = 1 м/с
h - высота водного потока русла реки = 1 м
n - количество слоёв водного потока = 3
L - длина водного потока русла реки = 1 м
a - ширина водного потока русла реки = 5 м
h слоя - высота одного слоя водного потока русла реки, м.
Определим высоту одного слоя водного потока реки:
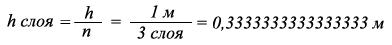
где:
h слоя - высота одного слоя водного потока русла реки, м
n - количество слоёв водного потока = 3
h - высота водного потока русла реки = 1 м.
Определим объём воды одного слоя протекающего по руслу реки:
V слоя = S · L = (0,3333333 м · 5 м) · 1 м = 1,666666666 м ³
где:
V слоя - объём одного слоя водного протока реки, м ³
S - площадь струи одного слоя водного протока реки, м ²
L - длина струи одного слоя водного потока реки, м.
Из физики мы знаем, что плотность воды при 20 °С,рв = 0,99823 г/см ³ или998,23кг/м ³.
Определим вес воды имеющего объём 1,6666666666 м ³, который проходит за 1 с:
G = V · pв = 1,6666666666 м ³ · 998,23 кг/м ³ = 1663,7166666 кг
где:
G - вес воды одного слоя водного потока, кг
V - объём воды одного слоя водного потока= 1,66666666665 м ³
рв - плотность воды при 20 °С = 998,23 кг/м ³.
Переведём вес воды, который находится в 1,6666 м ³ в Ньютоны:
9,80665 Н = 1 кгХ Н = 1663,7166666500295 кг.
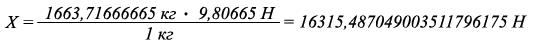
Необходимо учесть, что при перемещении каждого слоя водного потока в нём будут происходить потери силы, работы и энергии, где самые большие потери будут происходить в нижнем слое водного потока.
Например:
потери силы верхнего слоя водного потока составляют = 0,0876688206321233115Н
потери силы среднего слоя водного потока составляют = 0,1753376412642466236Н
потери силы нижнего слоя водного потока составляют = 0,2191720515803082787Н.
Необходимо также учесть,что безнапорное движениежидкости со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.д.)у которогоскорость и давление изменяются не только от координат пространства, но и от времени, считаетсянеустановившимся или нестационарным.Поэтому с учётомперемещения водного потока масса верхнего слоя находящегося над исследуемым слоем водного потока уменьшается и составляет приблизительно80 %от естественной массы верхнего слоя. Для точных расчётов нужен интегрированный подход,который включает множество составляющих этого технологического процесса происходящего во времени.
Зная силу, которая производит перемещение всего водного потока реки, мы можем определить период времени необходимый для перемещения одного слоя водного потока реки. Вся работа по перемещению всех трёх слоёв водного потока реки была произведена за 1 с.
Например, определим период времени необходимый для перемещения верхнего слоя водного потока реки по новому закону:
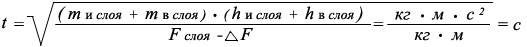
где:
t - период времени необходимый для перемещения одного исследуемогослоя водного потока, с
F - сила для перемещения всего водного потока = 16315,487049003511796175Н
Δ F - потеря силы по перемещению каждого слоя водного потока = 0,087668820632123Н
m и слоя - масса исследуемого слоя водного потока (верхнего) = 1663,716666666кг
m в слоя - масса верхнего слоя находящегося над исследуемым слоем= 0 кг
h и слоя - высота исследуемого слоя водного потока (верхнего) = 0,333333333 м
h в слоя - высота верхнего слоя находящегося над исследуемым слоем= 0 м.
Например, определим период времени необходимый для перемещения среднего слоя водного потока реки по новому закону:
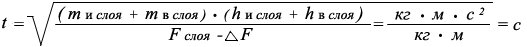
где:
t - период времени необходимый для перемещения одного исследуемогослоя водного потока, с
F - сила для перемещения всего водного потока = 16315,487049003511796175Н
Δ F - потеря силы по перемещению каждого слоя водного потока = 0,1753376412642466Н
m и слоя - масса исследуемого слоя водного потока (среднего) = 1663,716666666кг
m в слоя - с учётомперемещения водного потока масса верхнего слоя находящегося над исследуемым слоем водного потока уменьшается и составляет приблизительно80 %от естественной массы верхнего слоя, что составляет 1330,9733333328кг
h и слоя - высота исследуемого слоя водного потока (среднего) = 0,333333333 м
h в слоя - высота верхнего слоя находящегося над исследуемым слоем= 0,333333333м.
Например, определим период времени необходимый для перемещения нижнего слоя водного потока реки по новому закону:
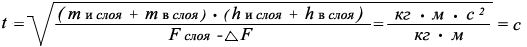
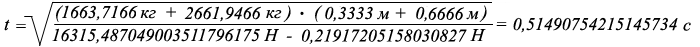
где:
t - период времени необходимый для перемещения одного исследуемогослоя водного потока, с
F - сила для перемещения всего водного потока = 16315,487049003511796175Н
Δ F - потеря силы по перемещению каждого слоя водного потока = 0,2191720515803082 Н
m и слоя - масса исследуемого слоя водного потока (нижнего) = 1663,716666666кг
m в слоя - с учётомперемещения водного потока масса верхних слоёв находящихся над исследуемым слоем водного потока уменьшается и составляет приблизительно80 %от естественной массы верхних слоёв, что составляет2661,9466666656кг
h и слоя - высота исследуемого слоя водного потока (среднего) = 0,333333333м
h в слоя - высота верхнего слоя находящегося над исследуемым слоем= 0,666666666м.
Произведём проверку количества секунд затраченных на перемещение водного потока реки имеющего объём 5 м ³.
0,184365731839 с+0,349810320892 с+0,514907542151 с=1,049083594882 c
Как нам стало известно из нового закона, что даже при ламинарном перемещении жидкости в водном потоке реки каждый слой водного потока испытывает потери в силе, работе и энергии. Если водный поток проходит по переменному сечению горизонтальной трубы или устью реки необходимо учитывать ещё общие потери в переменном сечении устья реки или горизонтальной трубы включающие:
- потери силы водного потока на перемещение каждого слоя,
- потери температурные внутри каждого слоя водного потока,
- потери работы водного потока на перемещение каждого слоя,
- потери энергии водного потока на перемещение каждого слоя,
- потери времени на перемещение каждого слоя водного потока,
- потери на трение водного потока о стенки трубы или устье реки,
- потери от химического состава и механических свойств жидкости,
- потери от физических свойств и кинематической вязкости жидкости, - потери силыв сужающем устройстве при перемещении водного потока,- потери работыв сужающем устройстве при перемещении водного потока,- потери энергиив сужающем устройстве при перемещении водного потока и т д…
Необходимо напомнить, что вода обладает аномальной высокой теплоёмкостью [4,18 Дж/(г · К)], то есть вода медленно нагревается и медленно остывает, таким образом,являясь регулятором температуры.
Для перемещения жидкости по переменному сечению горизонтальной трубы часто используют закон Бернулли, который является, как бы следствием закона сохранения энергии. Необходимо отметить, что закон Даниила Бернулли не соответствует размерным единицам физических величин и не учитывает множество потерь при перемещении водного потока или жидкой смеси по переменному сечению трубопровода.
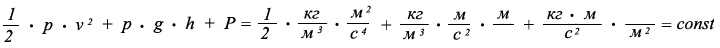
где:
h - уровень жидкости, мм
v - скорость перемещения жидкости, м/с ²
p - плотность перемещаемой жидкости, кг/м ³
g - ускорение свободного падения тел в пространстве, м/с ²
P - давление перемещаемой жидкости, Па где: 1 Па = 1 Н/м ².
2. Новый закон, определяющий момент силы для перемещения водного потока или жидкой смеси проходящей по переменному сечению трубопровода или устья реки, можно сформулировать так:
Момент силы для перемещения водного потока или жидкой смеси проходящей по переменному сечению трубопровода или устья реки равен произведению плотности водной среды, ускорению свободного падения тел в пространстве, площади сечения водного потока и длины измеряемого водного потока на разницу потерь силы водного потока или жидкой смеси.
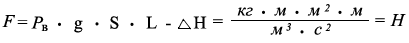
где:
Р в - плотность воды, кг/м ³
g - ускорение свободного падения тел в пространстве, м/с ²
L - длина измеряемого водного потока или жидкой смеси, м
F - сила для перемещения водного потока или жидкой смеси, Н
S - площадь сечения водного потока или трубопровода,внутрикоторого перемещается вода или жидкая смесь, м ²
Δ H - потери давления в трубопроводе или другом объёме,внутри которого перемещается водный поток или жидкая смесь, Н.
Примечание:
При измерении силы водного потока перемещающегося по руслу реки необходимо измерять площадь сечения водного потока по формуле:
S = a · h
где:
S - площадь сечения водного потока русла реки, м ²
a - ширина водного потока русла реки, м
h - высота водного потока русла реки, м.
При измерении силы водного потока перемещающегося внутри трубопровода необходимо измерять площадь сечения трубопровода по формуле:
S = П · r ²
где:
r - радиус трубопровода, м ²S - площадь сечения трубопровода, м ²П - 3,141592653589793238462643383...(отношение длины окружности к его диаметру) .
При этом необходимо особо подчеркнуть, что закон, который определяет момент силы водного потока, очень чувствителен к ускорению свободного падения тел в пространстве, поэтому механизм его возникновения был изложен в описании патента Российской Федерации № 2382232 от 19 сентября 2008 года.
3. Новый закон,определяющий работу перемещения водного потока или жидкой смеси проходящей по переменному сечению трубопровода или устья реки, можно сформулировать так:
Работа по перемещению водного потока или жидкой смеси проходящей по переменному сечению равна произведению плотности водной среды, ускорению свободного падения тел в пространстве, площади сечения водного потока и длины измеряемого водного потока на разницу потерь силы водного потока или жидкой смеси и на произведение расстояния пройденного пути измеряемого водного потока или жидкой смеси.
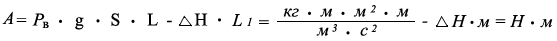
где:
А - работа по перемещению водного потока или жидкой смеси, Н · м
Р в - плотность воды, кг/м ³
g - ускорение свободного падения тел в пространстве, м/с ²
S - площадь сечения водного потока или трубопровода,внутри которого перемещается вода или жидкая смесь, м ²
L - длина измеряемого водного потока или жидкой смеси, м
L 1 - расстояние пройденного пути измеряемого водного потока или жидкой смеси, м
Δ H - потери давления в трубопроводе или другом объёме,внутри которого перемещается водный поток или жидкая смесь, Н.
4. Новый закон, определяющий энергию перемещения водного потока или жидкой смеси проходящей по переменному сечению, можно сформулировать так:
Энергия по перемещению водного потока или жидкой смеси проходящей по переменному сечению прямо пропорциональна произведению плотности водной среды, ускорению свободного падения тел в пространстве, площади сечения водного потока и длины измеряемого водного потока на разницу потерь силы водного потока или жидкой смеси и на произведение длины пройденного пути измеряемого водного потока или жидкой смеси и обратно пропорциональна периоду времени перемещения водного потока или жидкой смеси.
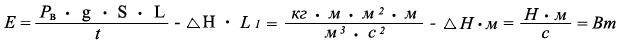
где:
Р в - плотность воды при 20 °С = 998,23 кг/м ³
g - ускорение свободного падения тел в пространстве, м/с ²
L - длина измеряемого водного потока или жидкой смеси, м
Е - энергия по перемещению водного потока или жидкой смеси, Вт
t - период времени перемещения водного потока или жидкой смеси, с
S - площадь сечения водного потока или трубопровода внутри которого перемещается вода или жидкая смесь, м ²
L 1 - расстояние пройденного пути измеряемого водного потока или жидкой смеси, м
Δ H - потери давления в трубопроводе или другом объёме,внутри которого перемещается водный поток или жидкая смесь, Н.
Новые законы Белашова соответствуют размерным единицам физических величин и по ним можно вычислить не только перемещение водного потока или жидкой смеси, но и перемещение воздушного потока или газовой смеси, где в законах необходимо заменить
Р в - плотность воды или жидкой смеси на
Р о - плотность воздушного потока или газовой смеси.
Например, рассмотрим трубопровод переменного сечения, внутри которого проходит водный поток имеющий:
L - длина трубопровода = 3 м
r - радиус трубопровода = 0,04 м
Р в - плотность воды при 20 °С = 998,23 кг/м ³
Δ Н - потери давления в трубопроводе = 0,005 Н
V - скорость водного потока или водной смеси = 3 м/с
L 1 - расстояние пройденного пути водного потока или жидкой смеси = 3 м.
Определим объём воды,который проходит по трубопроводу радиусом 0,04 м за 1 с:
V = П · r ² · L = 3,141592653589793238 · 0,04 ² · 3 = 0,01507964473723100754 м ³
где:
L - длина трубопровода, 3 м
r - радиус трубопровода, 00,4 м
V - объём воды,который проходит по трубопроводуза 1 с, м ³
П - 3,141592653589793238462643383...(отношение длины окружности к его диаметру).
Из физики мы знаем, что плотность воды при 20 °С, рв = 0,99823 г/см ³ или 998,23 кг/м ³.
Определим вес воды имеющего объём 0,01507964473723100754 м ³, который проходит по трубопроводу диаметром 0,08 м за 1 с.
G = V · pв = 0,01507964473723100754 м ³ · 998,23 кг/м ³ = 15,0529537660461086612667 кг
где:
G - вес воды находящегося в трубопроводе, кг
рв - плотность воды при 20 °С, кг/м ³
V - объём воды, м ³.
Переведём вес воды, который находится в 0,01507964473723100754м ³ в Ньютоны:
9,80665 Н = 1 кг
Х Н = 15,052953766046108661266709621557 кг.
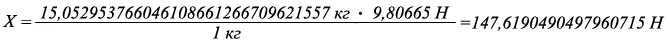
Определим работу водного потока проходящего по переменному сечению трубопровода:
A = F · L 1 = 147,6190490497960715031 Н · 1 м = 147,61904904979607150311 Н · м
где:
А - работа водного потока проходящего по переменному сечению трубопровода, Н · м
F - сила водного потока проходящего по переменному сечению трубопровода, Н
L 1 - расстояние пройденного пути водного потока или жидкой смеси = 3 м.
При этом потери при прохождении водного потока по трубопроводу переменного сечения составляют 0,005 Н.
Определим силу водного потока с потерями в трубопроводе:
F = 147,619049049796071503011 Н - 0,005 Н = 147,614049049796071503011 Н.
Силу перемещения водного потока, проходящего по трубопроводу имеющего площадь сечения трубопровода = 0,0050265482457436691815402294132472 м ²,вычислим по новому закону:
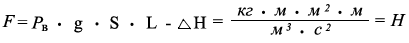
F = (998,23 · 9,80665 · 3,141592 · 0,0016 · 3) - 0,005 = 147,614049049796071503011 Н
где:
Р в - плотность воды при 20 °С = 998,23 кг/м ³
F - сила для перемещения водного потока или жидкой смеси, Н
L - длина измеряемого водного потока или жидкой смеси = 3 м
g - ускорение свободного падения тел в пространстве = 9,80665 м/c ²
Δ H - потери давления в трубопроводе или другом объёме внутри,которого перемещается водный поток = 0,005 Н.
S - площадь сечения водного потока или трубопровода внутри, которого перемещается вода или жидкая смесь вычислялась по формуле:
S = П · r ²
где:
r - радиус трубопровода = 0,04 м
S - площадь сечения трубопровода, м ²
П - 3,14159265358979323846264338327...(отношение длины окружности к его диаметру).
Точность определения силы по перемещению водного потока или жидкой смеси проходящей по переменному сечению трубопровода = 0,04 м на высоте имеющей ускорение свободного падения тел в пространстве = 9,80665 м/c ²составляет 100 %.
Силу для перемещения водного потока или жидкой смеси проходящей по переменному сечению водного потока реки имеющего площадь 5 м ² вычислим по новому закону:
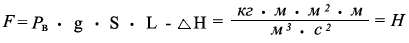
F = 998,23 · 9,80665 · 5 · 1 = 48946,4611475 Н
где:
Р в - плотность воды при 20 °С = 998,23 кг/м ³
F - сила для перемещения водного потока или жидкой смеси, Н
L - длина измеряемого водного потока или жидкой смеси = 1 м
g - ускорение свободного падения тел в пространстве = 9,80665 м/c ²
S - площадь сечения водного потока русла реки, внутри которого перемещается вода или жидкая смесь вычислялась по этой формуле:
S = a · h = 5 м · 1 м = 5 м ²
где:
S - площадь сечения водного потока русла реки, м ²
a - ширина водного потока русла реки = 5 м
h - высота водного потока русла реки = 1 м.
Точность определения силы, по перемещению водного потока проходящего по переменному сечению водного потока реки имеющего площадь 5 м ², на высоте имеющей ускорение свободного падения тел в пространстве= 9,80665 м/c ²составляет 100 %.
Необходимо особо подчеркнуть, что в данном законе очень важно знать, на какой высоте происходит данное перемещение водного потока реки и точные значения ускорения свободного падения тел в пространстве.
После открытия кинематической вязкости воздушного потока за единицу времени:
Б = 7,70212489908158646549242043365948 м ² /с
смотрите патент Российской Федерации № 2247860 под названием "Ветряной двигатель Белашова"икинематическойвязкостиводногопотоказаединицувремени:
Бв = 462,12749394489518792954522541906 м ² /с
смотрите патент Российской Федерации № 2277678 под названием "Гидрофизический кавитационный тепловой нагреватель Белашова" выяснилось:
Зная кинематическую вязкость водного и воздушного потока за единицу времени, можно вывести формулы для определения работы по перемещению жидкой или газообразной смеси по переменному сечению трубопровода. Данные формулы будут иметь правильную размерность физических величин и могут быть применены для жидких или газообразных сред имеющих разную кинематическую вязкость.
Работу по перемещению водного потока или жидкой смеси проходящей по переменному сечению трубопровода, можно вычислить, по первой формуле Белашова:
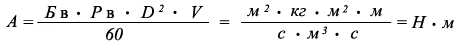
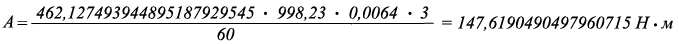
где:
Р в - плотность воды при 20 °С = 998,23 кг/м ³
V - скорость водного потока или водной смеси = 3 м/с
А - работа по перемещению водного потока или жидкой смеси, Н · м
Б в - кинематическая вязкость водного потока за единицу времени
при 20 °С = 462,12749394489518792954522541906 м ² /с
D - диаметр трубопровода, где проходит водный поток или водная смесь = 0,08 м.
Точность определения работы по перемещению водного потока или жидкой смеси проходящей по переменному сечению трубопровода, вычисленного по первой формуле Белашова,составляет - 0,00000000000000000000000032564 Н · м.
Работу по перемещению водного потока проходящей по переменному сечению русла реки имеющего площадь сечения водного потока = 5 м ² вычислим по первой формуле Белашова:
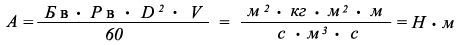
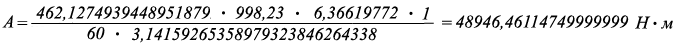
где:
D - диаметр водного потока реки, м
V - скорость водного потока реки = 1 м/с
Р в - плотность воды при 20 °С = 998,23 кг/м ³ S - площадь переменного сечения водного потока реки = 5 м ²
А - работа по перемещению водного потока проходящей по переменному сечению водного потока реки, Н · м Б в - кинематическая вязкость водного потока за единицу времени при 20 °С
= 462,12749394489518792954522541906 м ² /с
В первой формуле БелашоваD ² было определено по уже давно известной формуле:
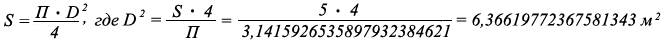
где:
D - диаметр трубопровода, м
S - площадь переменного сечения водного потока реки = 5 м ²
П - 3,1415926535897932384626433832...(отношение длины окружности к его диаметру).
Зная, как был вычислен условный диаметр водного потока проходящей по переменному сечению русла реки для первой формулы Белашова, то вторую формулу можно записать так:
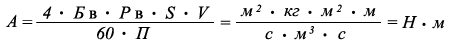
Например, определим работу по перемещению водного потока проходящей по переменному сечению русла реки имеющего площадь сечения водного потока = 5 м ² вычисленного по второй формуле Белашова:
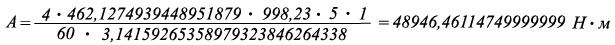
где: А - работа по перемещению водного потока проходящей по переменному сечению водного потока реки, Н · м
Б в - кинематическая вязкость водного потока за единицу времени при 20 °С
= 462,12749394489518792954522541906 м ² /с
П - 3,14159265358979323846264338327...(отношение длины окружности к его диаметру)
S - площадь переменного сечения водного потока реки = 5 м ²
Р в - плотность воды при 20 °С = 998,23 кг/м ³
V - скорость водного потока реки = 1 м/с.
Точность определения работы по перемещению водного потока или жидкой смеси проходящей по переменному сечению русла реки, вычисленного по второй формуле Белашова,составляет -0,00000000000000000000006361 Н · м.
Как видно из представленных расчётов сила, работа и энергия перемещения водных потоков по переменному сечению в трубе или устье водного потока реки полностью доказана по новым законам и математическим формулам Белашова, которые соответствуют закону сохранения энергии и ещё раз доказывает открытие кинематической вязкости воздушного потока за единицу времени:
Б = 7,70212489908158646549242043365948 м ² /с
и открытие кинематической вязкости водного потока за единицу времени:
Бв = 462,12749394489518792954522541906 м ² /с.
Ускорение свободного падения тел в пространстве сильно влияет на все процессы перемещения твёрдых и жидких тел на планете Земля. Так как в Российской Федерации, даже на законодательном уровне нет таких понятий как открытие, то механизм и закон образования ускорения свободного падения тел в пространстве был хорошо изложен в заявках на изобретение:
№ 2005129781/06 (033405) от 28 сентября 2005 года,
№ 2005140396/06 (033405) от 26 декабря 2005 года.
В заключении можносказать, что предложенные для вашегорассмотрения новые законы и математические формулы по гидродинамике,подтверждают, что наш материальный мир очень многообразен и все процессы, совершаемые в нём от случайно сложившихся обстоятельств, которые происходят во времени, в разной мере, влияют один на другой. В этом мире всё переплетено, и одно явление природы в разной мере находиться в зависимости к другому, поэтому не может быть постоянных констант,законовилифизическихвеличин, которые бы существовали независимо один от другого. В связи с этим выдвигается новая теория многогранной зависимости. Например,перемещение жидкости по переменному сечению трубопровода или устью реки тесно связано с законом ускорения свободного падения тел в пространстве, температурой и кинематической вязкостью жидкой смеси. В тоже время закон ускорения свободного падения тел в пространстве тесно связан с новым законом тяготения между двумя материальными телами, которые расположены в пространстве Солнечной (или другой) системы и новым законом тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу). Перечисленные законы тяготения находятся в постоянной зависимости от нового закона энергии между двумя материальными телами, которые находятся в пространстве Солнечной (или другой) системы и нового закона энергии одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу) и многим другим. Поэтому для любых расчётов нужен интегрированный подход,который будет включать множество составляющих любого технологического процесса происходящего во времени.
Литература
1. "Единцы физических величин и их размерности". Автор Л.А.Сена. Издательство "Наука" Москва 1988 год страницы 64-80.
2. "Ветряной двигатель Белашова".Автор А.Н. Белашов. Патент Российской Федерации № 2247860 от 22 сентября 2003 года.
3. "Гидрофизический кавитационный нагреватель Белашова".Автор А.Н. Белашов. Патент Российской Федерации № 2277678 от 18 ноября 2004 года.
4. "Бесплотинная гидроэлектростанция Белашова". Автор А.Н. Белашов. Патент Российской Федерации № 2382232 от 19 сентября 2008 года.
5. "Новые законы и математические формулы по гидродинамике". Автор А.Н. Белашов URL: http://www.belashov.info/SGIDRO/s-gidro.htm
6. "Открытия, изобретения, новые технические разработки". Автор А.Н. Белашов URL: http://www.belashov.info/index.html
7. "Новая теория многогранной зависимости". Автор А.Н. Белашов URL: http://www.belashov.info/LAWS/theory.htm
8. "ГравитационноеустройствоБелашова",описаниезаявкинаизобретение № 2007126789 от 16 июля 2007 года стр.15.
9. "Устройство вращения магнитных систем Белашова",описание заявкина изобретение № 2005129781 от 28 сентября 2005 года стр.9.
10. "Силы в природе", В.И.Григорьев, Г.Я.Мякишев, Москва "Наука" 1988 года.
11. "Датчики контроля и регулирования".Авторы Д.И. Агейкин Е.Н Костина, Н.Н Кузнецова. Издательство «Машиностроение» Москва 1965 г.стр. 692.