INFLUENCE OF POWER CIRCUIT LINKS OSCILLATIONS DYNAMIC CONNECTEDNESS ON TORSIONAL VIBRATIONS PROPAGATION CHARACTER IN THE SHAFTING

Шеховцов В.В.¹, Ляшенко М.В.², Шевчук В.П.³, Соколов-Добрев Н.С.⁴, Шеховцов К.В.⁵

¹Доктор технических наук, доцент; ² доктор технических наук, профессор, ³кандидат технических наук, профессор, ⁴кандидат технических наук, доцент, ⁵аспирант; Волгоградский государственный технический университет

ВЛИЯНИЕ ДИНАМИЧЕСКОЙ СВЯЗАННОСТИ ЗВЕНЬЕВ СИЛОВОЙ ЦЕПИ НА ХАРАКТЕР РАСПРОСТРАНЕНИЯ КРУТИЛЬНЫХ КОЛЕБАНИЙ В ВАЛОПРОВОДЕ

Аннотация

Описаны результаты исследований с помощью созданной компьютерной программы влияния коэффициента динамической связанности колебаний звеньев на характер распространения колебаний по валопроводу силовой передачи.

Ключевые слова: силовая передача, крутильные колебания, динамическая связанность колебаний.

Shekhovtsov V.V.¹, Lyashenko M.V.², Shevchuk V.P.³, Sokolov-Dobrev N.S.⁴, Shekhovtsov K.V.⁵

¹Doctor of Engineering Science, docent; ²Doctor of Engineering Science, professor; ³Candidate of engineering science, professor; ⁴Candidate of engineering science, docent; ⁵Post-graduate student; Volgograd State Technical University

INFLUENCE OF POWER CIRCUIT LINKS OSCILLATIONS DYNAMIC CONNECTEDNESS ON TORSIONAL VIBRATIONS PROPAGATION CHARACTER IN THE SHAFTING

Abstract

The article describes the results of research (using the computer program) of the influence of the vibration units dynamic coupling coefficient on the nature of oscillation propagation on the power transmission shafting.

Keywords: power train, torsional vibration, oscillations dynamic connectivity.

1. Введение

Известно [2, 3, 4, 5, 6, 7, 8, 9], что в одних силовых передачах крутильные колебания определенной частоты проходят через весь валопровод практически без гашения, а в других они гасятся на соседних с источником участках.

Изучением процесса распространения колебаний в связанных динамических системах занимался профессор Мандельштам Л. И. В его работах показано, что на процесс распространения колебаний оказывает влияние степень динамической связанности колебаний звеньев системы. Процесс распространения колебаний изучался на примере движения двух маятников [1], соединенных упругой связью. При этом установлено, что если парциальная частота колебаний одного звена этой системы (одного маятника) равна парциальной частоте другого звена (другого маятника), то колебания быстро и практически без гашения передаются от одного звена к другому.

Некоторые положения этих работ могут быть использованы для исследования характера распространения крутильных колебаний в силовых приводах машин [6, 7, 8, 9], являющихся n-массовыми системами, совершающей связанные колебания.

2. Определение степени динамической связанности колебаний звеньев

Для простоты рассмотрим двухзвенную крутильно колеблющуюся модель системы с вращательным движением [2, 4, 6, 8, 9], включающую в себя три массы, соединенные двумя упругими связями (рис. 1). Под звеном будем понимать участок модели, связывающий две колеблющиеся массы.

Рис. 1. Двухзвенная модель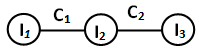

Дифференциальные уравнения свободных колебаний звеньев такой модели можно записать в следующем виде:

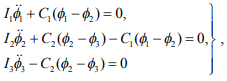                                                           (1)

где I_i  – моменты инерции масс; С_i – крутильная жесткость их связей;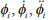 – угловые перемещения, скорости и ускорения масс соответственно.

Введем новые переменные:

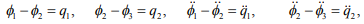                     (2)

где q_i  и 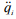– относительные угловые перемещения и ускорения звеньев соответственно.

Проведя ряд преобразований, в итоге получим систему из двух уравнений:

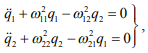                                                                               (3)

где 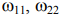– парциальные частоты звеньев, причем

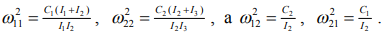
Частотное, или характеристическое уравнение системы (3) записывается в виде

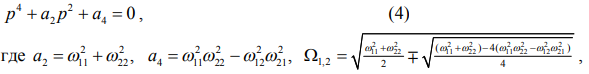
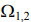– частоты собственных колебаний.

В соответствии с [1], максимальное взаимное влияние колебаний звеньев, или их максимальная динамическая связанность, имеет место при равенстве их парциальных частот, то есть при 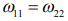, а степень динамической связанности колебаний звеньев определяется отношением

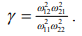                                                                                     (5)

Параметр g называют коэффициентом динамической связанности колебаний звеньев. Он получается из рассмотрения характеристического уравнения (4) и показывает степень отличия от нуля свободного члена а₄. Когда

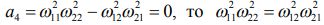
и коэффициент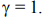

Каков физический смысл этого коэффициента? При 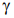<< 1 динамическая связанность звеньев мала – при свободных колебаниях каждое из них будет совершать колебания с частотой, близкой к парциальной, то есть с той, с которой это звено совершало бы колебания, не будучи в составе системы. При этом влияние других звеньев на частоту колебания каждого отдельного звена ничтожно мало. Чем дальше значение коэффициента g от нуля, тем более возрастает динамическая связанность звеньев, тем более отличаются собственные частоты их колебаний от парциальных и становятся присущими всей системе, а не ее локальным парциальным элементам.

3. Влияние степени динамической связанности звеньев

на характер распространения крутильных колебаний

Исследования выполнены на основе трехзвенной системы [8, 9, 10]. В табл. 1 приведены значения моментов инерции масс и коэффициента динамической связанности g при одинаковой жесткости всех связей системы, равной 100000 Н×м/рад.

Таблица 1 Влияние моментов инерции масс на степень динамической связанности колебаний звеньев

№№ п/п	Моменты инерции масс, кг×м2				Значение
	I1	I2	I3	I4
1	0,001	1	1	1	0,2630
2	0,01	1	1	1	0,2650
3	0,1	1	1	1	0,3075
4	1	1	1	1	0,5261
5	10	1	1	1	0,7057
6	100	1	1	1	0,7454
7	1000	1	1	1	0,7512
8	10000	1	1	1	0,7510
9	0,001	1	0,001	1	0,9980
10	0,001	1	0,01	1	0,9803

Как видно из табл. 1, изменение момента инерции первой массы системы от 0,001 до 10000 кг×м² (варианты 1 ‑ 8) вызывает изменение коэффициента g только в пределах 0,263 ‑ 0,7512, то есть за счет изменения момента инерции одной массы системы от самого нижнего до самого верхнего пределов (для силовых передач автотранспортных средств) не удается достичь сильной динамической связанности ее звеньев [2, 5, 6, 10]. При изменении же момента инерции еще одной массы системы возможно получение близких к единице значений g (варианты 9 и 10). Во время исследований колебания на первой массе возбуждались единичным моментом с частотой 1 Гц и анализировался процесс передачи колебательной энергии от одного звена к другому.

Анализ результатов показывает, что при слабой динамической связанности (варианты 1, 4, 7) звеньев не прослеживается закономерность в передаче колебательной энергии от одного звена к другому (рис. 2), при сильной же связанности (рис. 3, вариант 9) значения потенциальной энергии второго и третьего звеньев в каждый момент времени оказываются одинаковыми [2, 3, 4, 9]. Символами W1, W2 и W3 обозначены величины потенциальной энергии закрутки соответствующих участков при колебаниях.

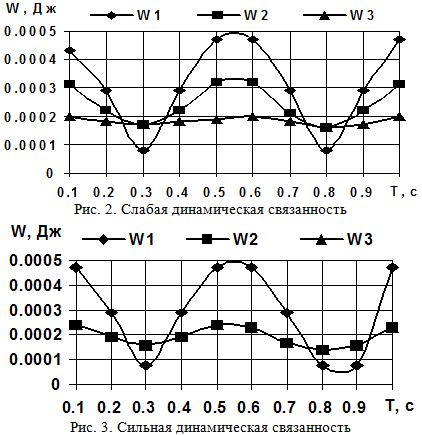
Рис. 3. Сильная динамическая связанность

Из рассмотрения выражения для определения значения коэффициента 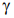 следует, что его значение будет тем более велико, чем более велика разница между произведениями собственных и парциальных частот звеньев системы. В табл. 2 приведены значения собственных и парциальных частот вариантов системы из табл. 1.

Таблица 2 Собственные и парциальные частоты вариантов системы

№№ п/п	Собственные частоты, Гц			Парциальные частоты, Гц
	1	2	3	1	2	3
1	50	87	1592	10000	447	447
2	50	87	505	3180	447	447
3	49	86	167	1050	447	447
4	38	71	92	447	447	447
5	25	63	90	332	447	447
6	22	62	90	318	447	447
7	22	62	90	316	447	447
8	22	62	90	316	447	447
9	50	1592	2251	10000	10000	10000
10	50	713	1592	10000	3180	3180
11	50	230	1592	10000	1050	1050

Данные табл. 2 свидетельствуют о том, что из рассмотренных только вариант 9 характеризуется тем, что при сильной динамической связанности колебаний все звенья системы имеют одинаковую парциальную частоту колебаний. Для того, чтобы проверить, как этот факт влияет на процесс распространения энергии колебаний, выполнено исследование еще нескольких вариантов модели с сочетаниями упруго-инерционных параметров, приведенными в табл. 3, при которых имеет место одинаковая парциальная частота колебаний всех звеньев [9, 10].

Таблица 3 Варианты с одинаковой парциальной частотой

№№ п/п	Жесткость связей, Н×м/рад			Моменты инерции масс, кг×м2				Парциальные частоты, Гц			Значе-ние g
	1	2	3	1	2	3	4	1	2	3
1	102	102	102	1	10-3	1	10-3	316	316	316	0,9982
2	10	10	10	1	10-3	1	10-3	100	100	100	0,9980
3	103	103	103	1	10-3	1	10-3	104	104	104	0,9980
4	104	104	104	1	10-3	1	10-3	104	104	104	0,9980

Для каждого из этих вариантов энергия закрутки первого и второго участков системы все время одинакова, то есть подтверждается положение о том, что для передачи одинаковых значений колебательной энергии от участка к участку необходимым условием является наличие сильной динамической связанности колебаний звеньев системы и одинаковых значений парциальных частот их колебаний [2, 3, 4, 5].

Влияет ли частота сигнала возбуждения на характер процесса распространения колебательной энергии? Для получения ответа на этот вопрос выполнено исследование для вариантов системы с одинаковыми парциальными частотами звеньев при возбуждении колебаний с частотами 0,1 Гц, 5 Гц и 10 Гц [2, 4, 5, 6]. Для примера результат с сигналом частотой 0,1 Гц приведен на рис. 4.

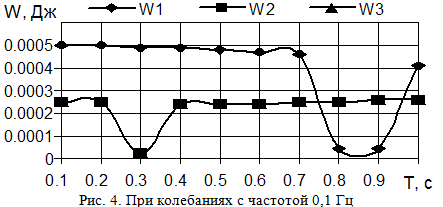
Анализ зависимостей на рис. 4 свидетельствует о том, что изменение частоты сигнала возбуждения не оказывает влияния на характер передачи колебательной энергии между вторым и третьим участками системы – кривые W2 и W3 совпадают. С увеличением частоты сигнала возбуждения до 10 Гц значения средней потенциальной энергии закрутки участков в каждый момент времени становятся одинаковыми.

Приведенные результаты получены на основе изучения свойств четырехмассовой системы. Насколько они справедливы для систем с большим числом масс? Для получения необходимых данных выполнены исследования характера распространения колебательной энергии шестимассовой и семимассовой системами, которые получены на основе четырехмассовой системы путем добавления звеньев с таким же чередованием значений моментов инерции масс [8, 9, 10]. Для примера результаты исследования для семимассовой системы приведены на рис. 5.

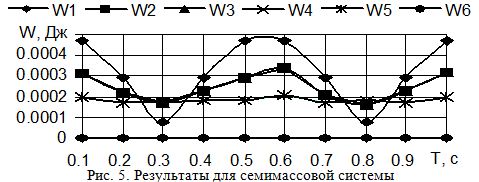
Анализ результатов всего комплекса выполненных исследований позволил выявить ряд закономерностей, которому подчиняется характер распространения крутильных колебаний в системах с вращательным движением. Они отражены в выводах.

4. Выводы

Характер передачи энергии крутильных колебаний от одного участка в системах с вращательным движением к другому определяется сочетанием упруго-инерционных параметров их элементов и порядком их соединения. Энергия колебаний от участка к участку передается без потерь, если выполняются следующие условия:

а) динамическая связанность колебаний звеньев системы сильная;

б) парциальные частоты колебаний всех звеньев системы одинаковы;

в) передача энергии осуществляется от участка, начинающегося массой с большим моментом инерции и заканчивающегося массой с малым моментом инерции, на участок, начинающийся массой с малым моментом инерции и заканчивающийся массой с большим моментом инерции, причем значение большего момента инерции должно минимум на порядок превышать значение меньшего.