HYPERCOMPACT DETERMINISTIC HYBRID STRUCTURES BASED ON SOME MULTITUDE INTERPENETRATING FRACTAL SUB-LATTICES ON SQUARE NET
Иванов В.В.
Кандидат химических наук, доцент, Южно-Российский государственный технический университет (Новочеркасский политехнический институт)
ГИПЕРКОМПАКТНЫЕ ДЕТЕРМИНИСТИЧЕСКИЕ ГИБРИДНЫЕ СТРУКТУРЫ НА ОСНОВЕ МНОЖЕСТВА ВЗАИМОПРОНИКАЮЩИХ ФРАКТАЛЬНЫХ ПОДРЕШЕТОК НА КВАДРАТНОЙ СЕТКЕ
Аннотация
Обсуждается возможность формирования гиперкомпактных детерминистических гибридных структур на основе определенного множества взаимопроникающих фрактальных подрешеток на квадратной сетке.
Ключевые слова: модуль, гибридный генератор, гиперкомпактная фрактальная структура.
Ivanov V.V.
PhD in Chemistry, associate professor, South-Russian state Еngineering University (Novocherkassk Polytechnic Institute)
HYPERCOMPACT DETERMINISTIC HYBRID STRUCTURES BASED ON SOME MULTITUDE INTERPENETRATING FRACTAL SUB-LATTICES ON SQUARE NET
Abstract
The forming possibility of the hyper-compact deterministic hybrid structures based on some multitude interpenetrating fractal sub-lattices on square net is discussed.
Keywords: module, hybrid generator, hyper-compact fractal structure.
Формально существуют два способа получения генераторов гиперкомпактных фрактальных структур. Оба способа основаны на принципе минимизации доли лакунарного пространства в генераторе, заданном в единичной пространственной ячейке, например в единичной ячейке [0…1; 0…1] квадратной сетки. Вид (инъективный или сюръективный) итерационного формирования фрактальной структуры не влияет на процесс ее гиперкомпактификации. [1, 2]. При инъективном итерировании гиперкомпактный фрактал образуется в ячейке. Позиционное и ориентационное упорядочение этих фракталов во всем ячеистом пространстве приводит к образованию детерминистической фрактальной структуры, представляющей собой бесконечное множество локальных фракталов [3 - 10].
Первый способ гиперкомпактификации основан на использовании гомологического закона изменения конфигурации некоторого генератора. При этом в ряду генераторов-гомологов будет закономерно изменяться и фрактальная размерность. Для бесконечного члена гомологического ряда фракталов размерность будет совпадать с размерностью ячеистого пространства. В частности, для гомологического ряда структур CS(4n(n+1)/(2n+1)), основанных на классическом ковре Серпинского (рис.1), локальная размерность каждой из них определяется следующим образом:
Dim CS(4n(n+1)/(2n+1)) = ln(4n(n+1)) / ln (2n+1)
и при n = ¥ равна 2.
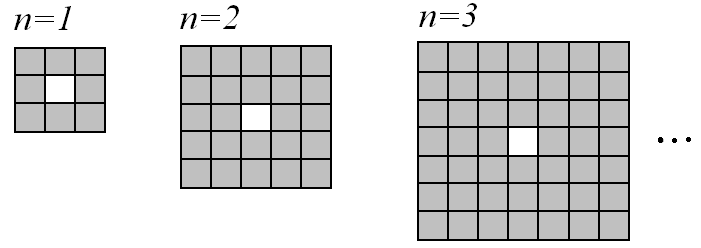
Рис.1 – Генератор классического ковра Серпинского CS(8/3) и два его ближайших гомолога из ряда генераторов CS(4n(n+1)/(2n+1)).
Второй способ основан на формировании гибридного генератора из двух простых структурно совместимых в пространственной ячейке генераторов с одинаковым коэффициентом подобия К. Если генераторы предполагаются невзаимодействующими, то их действие распространяется только на ту часть ячейки, которую они занимают в составном генераторе (рис.2). Гибридная компактная фрактальная структура характеризуется двумя взаимопроникающими подрешетками, а ее средневзвешенная локальная размерность является постоянной величиной, т.е.
<DimL> = DimL F(GenF1+GenF2) = K[N1 DimL (GenF1) + N2 DimL (GenF2)],
DimL (GenFi) = (lnNi / ln(K-1/2)),
где N1 и N2 - числа занятых подъячеек в соответствующих генераторах, (N1+N2) = K-1.
В качестве примера рассмотрим некоторые простые симметричные (G22 = p4mm) фрактальные структуры в 2D пространстве с К = 1/9: фрактал Вичека (FV, Dim = 1,465), фрактал на основе канторова множества точек (CM2, Dim = 1,262), ковер Серпинского (CS, Dim = 1,893) [1, 2] и соответствующие их дополнения: Ромб (Rh, Dim = 1,262), Крест (Cr, Dim = 1,465) и Точка (P, Dim = 0).
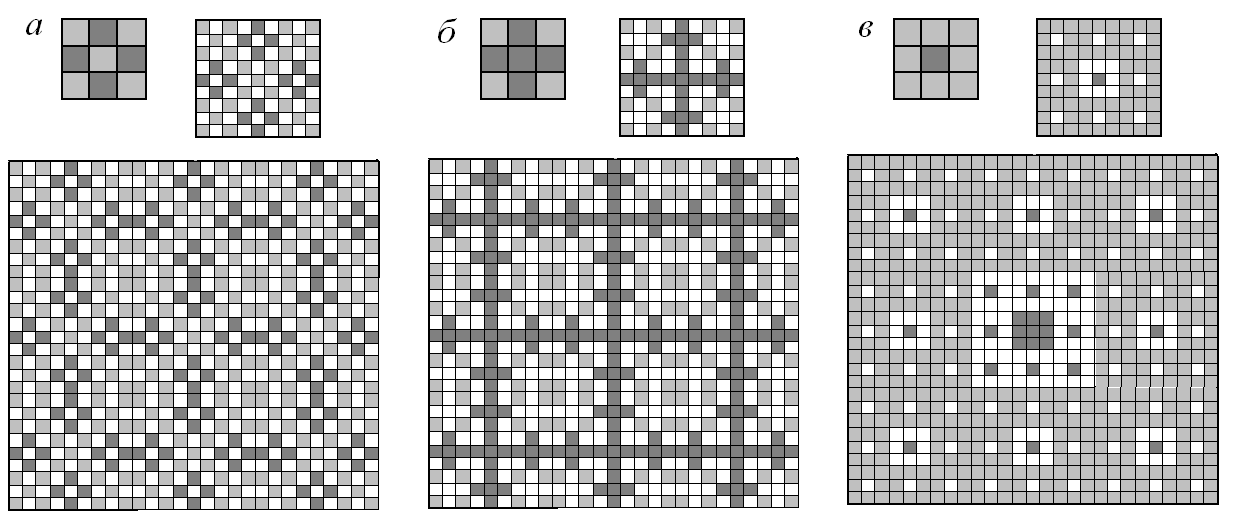
Рис.2 – Изображения гибридных генераторов (FV+Rh) (а), (CM2+C) (б), (CS+P) (в) и соответствующих им гиперкомпактных генераторов-предфракталов 2-го и 3-го поколения в квадратной единичной ячейке 2D пространства.
Для дальнейшей компактификации гибридной фрактальной структуры ее генераторы предполагаются взаимодействующими. В этом случае образующийся предфрактал 2-го поколения является гибридным генератором для формирования предфрактала 3-го поколения, который, в свою очередь, является генератором для предфрактала 4-го поколения и т.д (рис.2). Таким образом, имеем эволюционирующий с каждой итерацией генератор, необходимый для достижения максимально компактной структуры. Соответствующим образом изменяются и размерности каждого эволюционного предфрактала-генератора
Dim Fi-1, I = Dim Gen Fi-1, I = (2(i-2)/i) + i-1 DimGenF1,2 ,
монотонно приближаясь при i ® ¥ к своему естественному пределу
DimFi |i=¥ = 2.
Таблица 1 – Свойства некоторых симметричных (G22 = p4mm) гибридных фракталов, компактно сформированных в квадратной ячейке 2D пространства.
|
Наименование |
Гибридный генератор 2-го поколения |
Поколение генератора-предфрактала |
<DimL> |
DimG |
|
Фрактал Вичека и Ромб (Rhombus) и Множество канторовых множеств и Крест (Cross) |
(FV+Rh) и (CM2+Cr) |
2 3 4 10 |
1,680 1,787 1,840 1,936 |
2 |
|
Ковер Серпинского и Точка (Point) |
(CS+P) |
2 3 4 10 |
1,899 1,937 1,950 1,980 |
2 |
Полученные данные о гиперкомпактных детерминистических гибридных фрактальных структурах могут быть использованы при интерпретации некоторых эволюционных процессов, протекающих на поверхности активных анодных покрытий [11-13] и композиционных материалов и покрытий с антифрикционными свойствами [14-20] при их функционировании.
Литература
1. Фракталы в физике. Под ред. Л. Пьетронеро и Э. Тозатти. – M.: Мир, 1988. - 420 с.
2. Федер Е. Фракталы. - M.: Мир, 1991. - 260 с.
3. Иванов В.В., Таланов В.М. Принципы модулярного строения регулярных фрактальных структур // Успехи соврем. естествознания, 2012. - №3. – С.56-57.
4. Иванов В.В., Демьян В.В., Таланов В.М. Эволюционная модель формирования и анализ детерминистических фрактальных структур // Успехи соврем. естествознания, 2012. - №4. – С.230-232.
5. Иванов В.В. Принципы формирования регулярных простых фрактальных структур // МНИЖ, 2013. - №7. – С.-.
6. Иванов В.В. Общая характеристика возможных гибридных мономодулярных фрактальных структур// Соврем. наукоемкие технологии. 2013.- №.5. – С.29-31.
7. Иванов В.В. Формирование фрактальных структур на основе итерационной последовательности и канторова множества точек с заданными характеристиками в 1D пространстве // Успехи соврем. естествознания, 2013. - №8. – С.136-137.
8. Иванов В.В. Описание и классификация точечных мономодулярных фрактальных структур // Успехи соврем. естествознания, 2013. - №8. – С.134-135.
9. Иванов В.В. Анализ возможности получения новых точечных и квазиточечных фрактальных структур на основе итерационной последовательности и канторова множества// Успехи соврем. естествознания, 2013. - №8. – С.129-130.
10. Иванов В.В. Формирование и символьное описание детерминистических гибридных фрактальных структур в 2D пространстве // Соврем. наукоемкие технологии, 2013. - №.9 – С.89-93.
11. Иванов В.В. Комбинаторное моделирование вероятных структур неорганических веществ. – Ростов н/Д: Изд-во СКНЦ ВШ, 2003. – 204 с.
12. Bespalova Zh.I., Ivanov V.V., Smirnitskaya I.V., et al. Fabrication of a titanium anode with an active coating based on mixed oxides of base metals // Rus. J. Appl. Chem., 2010. - Т.83. - N.2. – С.242-246.
13. Ivanov V.V., Bespalova Zh.I., Smirnitskaya I.V., et al. Study of the composition of titanium anode with electrocatalytic coat based on cobalt, manganese, and nickel oxides // Rus. J. Appl. Chem., 2010. - Т.83. - N.5. – С.831-834.
14. Ivanov V.V., Balakai V.I., Ivanov A.V., Arzumanova A.V. Synergism in composite electrolytic nickel-boron-fluoroplastic coatings // Rus. J. Appl. Chem., 2006. - Т.79. - №4. - С.610-613.
15. Ivanov V.V., Balakai V.I., Kurnakova N.Yu. et al. Synergetic effect in nickel-teflon composite electrolytic coatings // Rus. J. Appl. Chem., 2008. - Т.81. - № 12. - С.2169-2171.
16. Balakai V.I., Ivanov V.V., Balakai I.V., Arzumanova A.V. Analysis of the phase disorder in electroplated nickel-boron coatings // Rus. J. Appl. Chem., 2009. - Т.82. - №.5. - С.851-856.
17. Иванов В.В., Щербаков И.Н. Моделирование композиционных никель-фосфорных покрытий с антифрикционными свойствами. – Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион», 2008. – 112 с.
18. Иванов В.В., Щербаков И.Н. Моделирование антифрикционных свойств композиционных покрытий с учетом вероятных конфигураций межфазных границ // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2011. - №3. - С.54-57.
19. Иванов В.В., Щербаков И.Н. Анализ возможных модификаторов для получения композиционных Ni-P покрытий с антифрикционными свойствами // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2011. - №5. - С.47-50.
20. Дерлугян П.Д., Иванов В.В., Иванова И.В. и др. Поиск эффективных модификаторов для получения композиционных Ni-P покрытий с антифрикционными свойствами // Соврем. наукоемкие технологии. 2013.- №.5. – С.21-24.