APPLICATION OF THE COMBINED METHOD OF FINDING SOLUTIONS OF PARABOLIC TYPE EQUATIONS OF THE SECOND ORDER WITH CONSTANT COEFFICIENTS

Мухаметов Е.М. ¹, Мустафаев А.П. ²

^1,2Кандидат физико-математических наук, профессор, Семипалатинский государственный университет им. Шакарима, Республика Казахстан

ПРИМЕНЕНИЕ КОМБИНИРОВАННОГО МЕТОДА ДЛЯ НАХОЖДЕНИЯ РЕШЕНИЯ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

Аннотация

В данной работе делается попытка дать на элементарном уровне представления о применения комбинированного метода, т.е. метод характеристики и метод Фурье к решению одного линейного уравнения параболического типа второго порядка с постоянными коэффициентами.

Ключевые слова: Дифференциальные уравнения, функция нескольких переменных, уравнений параболического типа, метод Фурье, метод характеристики.

Mukhametov E.M. ¹, Mustaphaev A.P. ²

^1,2Semey State University named after Shakarim, Republic of Kazakhstan

APPLICATION OF THE COMBINED METHOD OF FINDING SOLUTIONS OF PARABOLIC TYPE EQUATIONS OF THE SECOND ORDER WITH CONSTANT COEFFICIENTS

Abstract

This paper attempts to give a basic idea about the application of the combined method, i.e. a method of the characteristics and the Fourier method to the solution of the linear equation of parabolic type of second order with constant coefficients.

Keywords: differential equations, function of several variables, equations of parabolic type, Fourier method, method of characteristics.

Многие задачи физики приводят к разысканию той или иной функции нескольких переменных. Для ее определения составляет дифференциальное уравнения в частных производных, которому должна удовлетворят искомая функция.

Большое значение особенно в прикладных вопросах имеет получение явных формул интегральных представлений решений дифференциальных уравнений в частных производных.

Наряду с общими методами принимаемые при нахождения общего интеграла упомянутых уравнений для каждого типа уравнений существует,  и некоторые специфические методы, с помощью которого могут быть решены те или иные задачи математической физики.

Полученные при помощи уравнений математической физики решения тех или иных задач дают нам математическое описание ожидаемого хода или вида физических явлений, описываемых этими уравнениями.

В настоящей работе делается попытка дать на элементарном уровне представления о применения комбинированного метода, т.е. метод характеристики и метод Фурье к решению одного линейного уравнения параболического типа второго порядка с постоянными коэффициентами. Известно, что уравнения

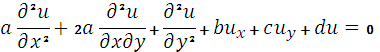                                      (1)

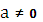где , и 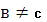 имеют одну характеристику

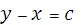 .                                                                                                                        (2)

В характеристических переменных

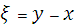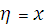,                                                                                                           (3)

уравнение (1) записывается в виде

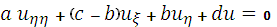                                                                    (4)

Далее вводим новую функцию

,                                                                                            (5)

где значение 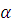 и 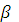 определим из системы

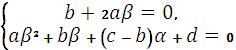                                                                               (6)

т.е.

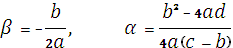                                                                                (7)

тогда (4) приводится более упрощенному уравнению вида

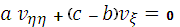.                                                                                             (8)

Для нахождения решения этого уравнения используем метод разделения переменных, т.е решения 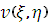 ищем в виде произведения

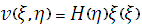,                                                                                                         (9)

где  - функция только переменного η, 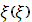  - функция только переменного ξ. Подставляя предполагаемую форму (9) в уравнение (8) получим

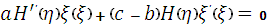                                                                   (10)

или после деления на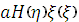 

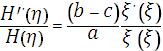 .                                                                                                (11)

Чтобы функция (9) была решением уравнения (8) равенство (11) должно удовлетворяться тождество.

Правая часть равенства (11)  является функцией только переменного 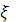, а левая только 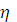, поэтому правая и левая части равенства (11) при изменений своих аргументов сохраняют постоянное значения. Это значение удобно обозначить через  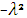 т.е.

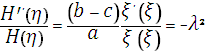.                                                                                   (12)

Из соотношения (12) получаем обыкновенные дифференциальные уравнения для определения 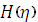 и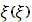 

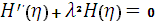,                                                                                               (13)

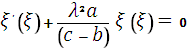.                                                                                      (14)

Общее решения уравнения (13) и (14) соответственно может быть записано в виде

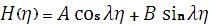,                                                                                (15)

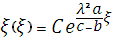                                                                                                           (16)

возвращаясь к старым переменным и подставляя (15), (16) в (9), заметили что функция

 

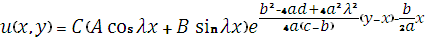
является частным видом общего решения уравнения (1).

Следует заметить полученные решения позволяет легко найти частное решения некоторых краевых задач для рассматриваемого уравнения.