ALGORYTHM DEVELOPMENT FOR CONTROL THE CERAMIC BLOCKS DYING AND BURNING PROCESES

Тиняков С.Е.¹, Андреев В.О.²

¹Кандидат технических наук, Филиал ФГАОУ ВПО «Сибирский федеральный университет» в г. Железногорске, г. Железногорск Красноярского края, ООО «Агро - Промышленная компания «ПаК», г. Красноярск; ²кандидат технических наук, ФГБОУ ВПО «Госуниверситет-учебно-научно-производственный комплекс», г. Орел

РАЗРАБОТКА АЛГОРИТМОВ УПРАВЛЕНИЯ ПРОЦЕССАМИ СУШКИ И ОБЖИГА КЕРАМИЧЕСКИХ БЛОКОВ С УЧЕТОМ ФОРМЫ И ТИПОРАЗМЕРОВ

Аннотация

Статья посвящена исследованию режимов управления температурой в процессах сушки и обжига керамических блоков, с учетом формы и типоразмеров изделий. Объектами исследования являются  алгоритмы управления температурой в процессах тепловой обработки керамических изделий. Приведено описание обобщенного уравнения тепловой обработки керамического тела, с учетом теплофизических характеристик и геометрии изделия. Рассмотрены методы автоматизации управления процессами тепловой обработки керамических тел, алгоритмы управления неустойчивыми процессами тепловой обработки с временным запаздыванием.

Ключевые слова: алгоритм управления температурой, временное запаздывание, керамический блок, обжиг, сушка, уравнение тепловой обработки.

Tinyakov S.Е.¹, Andreev V.O.²

¹PhD in Technical Sciences, Branch of Siberian Federal University; Agro-Industrial Company «PaK»; ² PhD in Technical Sciences, State university-Study-Science-Industrial complex

ALGORYTHM DEVELOPMENT FOR CONTROL THE CERAMIC BLOCKS DYING AND BURNING PROCESES

Abstract

The article considers to research of temperature control models in the drying and firing ceramic blocks processes depending on the shape and size of a product. The objects of study are algorithms of the temperature controlling process for a heat treatment of ceramic products. There are the generalized equation description of the ceramic block heat treatment, which depends on a thermal characteristics and geometry of the product. It also includes the automation methods of a ceramic blocks heat treatment processes and the control algorithms of a time-delay heat treatment unstable processes.

Keywords: temperature control algorithm, time-delay, ceramic block, firing, drying, heat treatment equation.

При разработке алгоритмов управления процессами сушки и обжига керамических блоков, с учетом их формы и типоразмеров, необходимо понимание теплофизики технологических этапов нагрева и охлаждения.

Для исследования процессов нагрева и охлаждения необходимо решить следующие задачи:

• сформулировать обобщенное уравнение тепловой обработки керамического тела с учетом геометрии изделия;
• предложить методы автоматизации управления процессами тепловой обработки керамических тел, с учетом геометрии изделий;
• на основе предложенных методов автоматизации управления, разработать алгоритмы управления нагревом и охлаждением керамических тел, с учетом геометрии изделий;
• предложить структуру системы автоматического управления температурой на основе ПИД регуляторов;
• исследовать алгоритмы управления неустойчивыми процессами тепловой обработки с временным запаздыванием;

1. Обобщенное уравнение тепловой обработки керамических тел, с учетом геометрии изделий

Рассмотрим процесс управления конвекционным теплообменом керамических тел с окружающей средой воздушной средой, имеющей постоянную температуру .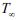

Пусть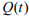 - некоторый параметр управления теплообменом, представляющий собой тепловой источник или компенсатор. Целью управления является регулирование температуры тела, манипулируя величиной параметра управления.

Один из критериев подобия стационарного теплообмена между нагретым и охлажденным твердым телом  - число Био (Bi) для керамического блока определяется как:

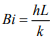
Здесь:

h -  коэффициент конвективного теплообмена - теплоотдачи от поверхности тела к окружающей среде (и наоборот);

L – характерный размер блока;

k – теплопроводность керамического тела.

В общем случае, процесс конвективного теплообмена керамического тела с окружающей средой описывается  квазилинейным линейным уравнением тепловодности. В предположении одинаковой температуры  точек керамического тела в процессе теплообмена, энергетический баланс между телом и окружающей средой апроксимируется дифференциальным уравнением первого порядка:

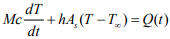                                                                               (1)

Здесь:

M – масса керамического тела;

c – удельная теплоемкость керамического вещества;

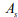 – площадь конвективной поверхности тела.

В сформулированной модели (1), геометрию изделия (форму и типоразмеры)  учитывает совокупность трех параметров – L,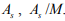

Перейдем к безразмерным переменным:

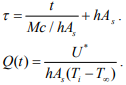
В таком случае, уравнение (1) принимает вид:                                                                                               

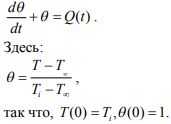                                                                               (2)

Уравнение (2) описывает управляемую систему. Обозначая параметр регулирования 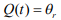, можно показать, что решение уравнения (2) (без запаздывания) имеет следующий вид:

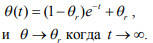                                                                                  (3)

2. Алгоритмы регулирования температуры керамического блока

Система автоматического управления с обратной связью для регулирования температуры керамического тела на основе уравнения (3) может быть, в общем виде,  представлена в следующем виде (рис. 1):

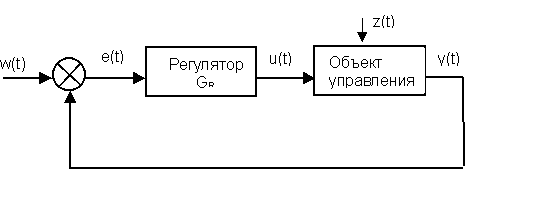
Рис. 1 Система автоматического управления с обратной связью

2.1 ПИД регулятор

Алгоритм пропорционально-интегрально-дифференциального управления по обратной связи (ПИД управление) определяется выражением:

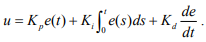                                                                        (4)

Здесь величина ошибки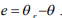

 

2.2 On-Off управление

Алгоритм определяется базовым уравнением [1]:

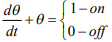                                                                                                 (5)

Решение уравнения (6) определяется как:

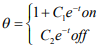                                                                                                  (6)

2.3 Пропорциональное управление с временным запаздыванием

Базовое уравнение для пропорционального управления в временной задержкой  определяется как [2]:

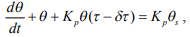                                                                          (7)

здесь 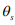- установочное значение.

Решение уравнения (7) имеет вид:

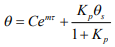,                                                                                            (8)

причем, при малых значениях , значение 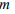аппроксимируется выражением:

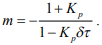
2.4 Управление при переменной температуре окружающей среды

Пусть температура окружающей среды изменяется синусоидально по закону:

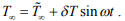
Тогда безразмерное базовое уравнение определится как:

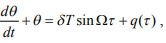                                                                             (9)

где

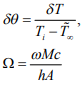                                                                                                  (10)

Одно из решений уравнения (10) представляется в виде:

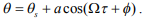
Здесь:

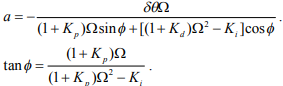
3. Исследование алгоритмов управления неустойчивыми процессами с временным запаздыванием

Будем рассматривать систему автоматизированного управления (температурный регулятор) с обратной связью, на основе ПИД контроллера, как показано на рис. 2.

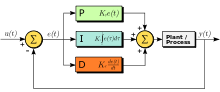
Рис. 2 Система автоматического управления с обратной связью на основе  ПИД-регулятора

При моделировании исследуемых алгоритмов, будем представлять управляемый процесс, с временным запаздыванием, неустойчивым звеном первого порядка:

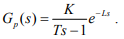                                                                                          (11)

Для лучшего понимания процесса регулирования рассматриваем период временного запаздывания в трех разных диапазонах нормализованного мертвого периода запаздывания [3]:

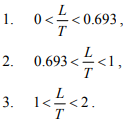
При изучении алгоритмов управления используется ряд технических параметров оценки качества управляемого процесса, в т.ч.:

• время подъема 
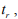
• время формирования  режима 
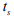
• перерегулирование
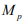
• интегральная абсолютная ошибка IAE,
• время восстановления после возмущения 
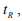
• максимальная ошибка вызванная возмущением 

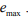
Заключение

В ходе выполнения работ получены следующие результаты:

• с учетом физики процессов  сушки и обжига керамических блоков, разработано обобщенное дифференциальное уравнение тепловой обработки с учетом геометрии и теплофизических характеристик изделий;
• на основе анализа научных публикаций, предложены методы автоматизации управления процессами тепловой обработки керамических тел, учитывающие геометрию изделий;
• исследованы подходы к управлению неустойчивыми процессами тепловой обработки, при наличии временного и мертвого запаздывания;
• предложена структура системы автоматического управления температурой на основе ПИД регуляторов, с учетом неустойчивости тепловых процессов и явления временного запаздывания;