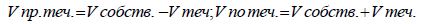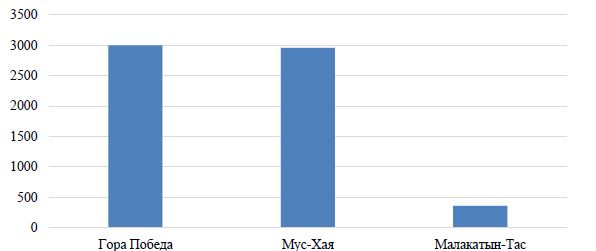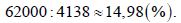LOCAL HISTORY MATERIAL IN MATHEMATICS LESSONS AS A MEANS OF FORMING THE EDUCATIONAL AND COGNITIVE COMPETENCE OF 5-6 GRADERS

КРАЕВЕДЧЕСКИЙ МАТЕРИАЛ НА УРОКАХ МАТЕМАТИКИ КАК СРЕДСТВО ФОРМИРОВАНИЯ УЧЕБНО-ПОЗНАВАТЕЛЬНОЙ КОМПЕТЕНЦИИ УЧАЩИХСЯ 5-6 КЛАССОВ

Научная статья

Дьячковская М.Д.¹, ^*, Кондакова К.В.² , Кондакова С.В.³

¹ ORCID: 0000-0001-8461-8235;

^1–3 Северо-Восточный федеральный университет, Якутск, Россия;

* Корреспондирующий автор (ter_rena777[at]mail.ru)

Аннотация

В статье рассматриваются некоторые вопросы использования элементов краеведения в обучении математике как средства формирования учебно-познавательной компетенции учащихся 5-6 классов. В качестве примера приводятся задачи и задания, разработанные на основе краеведческого материала Республики Саха (Якутия). Представлено описание педагогического эксперимента, проведенного на базе МБОУ «Тыайинская СОШ им. Н. Х. Дьяконова» Кобяйского улуса. Сделан вывод о том, что использование местного краеведческого материала на уроках математики способствует формированию у обучающихся способности к математическому познанию объектов и явлений окружающего мира и применению математических знаний на практике.

Ключевые слова: методика обучения математике, этнокультурный компонент, математические задачи с краеведческим содержанием, учебно-познавательная компетенция.

LOCAL HISTORY MATERIAL IN MATHEMATICS LESSONS AS A MEANS OF FORMING THE EDUCATIONAL AND COGNITIVE COMPETENCE OF 5-6 GRADERS

Research article

Dyachkovskaya M.D.¹, ^*, Kondakova K.V.² , Kondakova S.V.³

¹ ORCID: 0000-0001-8461-8235;

^1–3 North-Eastern Federal University, Yakutsk, Russia

* Corresponding author (ter_rena777[at]mail.ru)

Abstract

The article discusses some issues of using elements of local history in teaching mathematics as a means of forming the educational and cognitive competence of 5-6 graders. As an example, the tasks and problems developed on the basis of the local history material of the Republic of Sakha (Yakutia) are given. The description of the pedagogical experiment conducted on the basis of Tyayinsk Secondary school Of Kobyai ulus named after N.H. Diakonov is presented. It is concluded that the use of local history material in mathematics lessons contributes to the formation of pupils' ability to mathematically recognize objects and phenomena of the surrounding world and the application of mathematical knowledge in practice.

Keywords: methods of teaching mathematics, ethnocultural component, mathematical problems with local history content, educational and cognitive competence.

Введение

В современной региональной системе общего образования важное место в обучении математике занимает проблема развития учебно-познавательной компетенции учащихся школ с этнокультурным компонентом. Так, одна из основных задач учителя математики заключается в обеспечении качественного усвоения предметных знаний и умений учащимися, а также в создании педагогических условий для саморазвития личности каждого ученика в соответствии с его интересами, духовно-нравственными и жизненными ценностями.

Согласно Федеральному государственному образовательному стандарту (ФГОС) изучение математики должно формировать представления о социальных, культурных и исторических факторах становления математической науки, представление о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления [9]. В данном направлении несомненный методический потенциал имеет включение в содержание обучения элементов народной математики, а также составление и решение задач на историческом и краеведческом материале.

Различные аспекты теории и практики использования краеведческого материала в обучении математике содержатся в трудах А.П. Аргуновой [1], Л.Ю. Бучневой [2], А.В. Завалиной, О.А. Шаповал, О.Ю. Ходыревой [4], Н.И. Мерлиной [5; 6], С.С. Салаватовой, М.Ю. Солощенко [7], А.У. Уртеновой [8], М.М. Шихшинатовой [11], где дается научное обоснование того, что решение и составление задач на краеведческом и историческом материале способствуют повышению интереса и познавательной активности учащихся 5-6 классов, помогают сделать обучение математике более содержательным.

В данной работе использование краеведческого материала и задач с краеведческим содержанием в обучении математике выступает как одно из средств формирования учебно-познавательной компетенции учащихся. В качестве рабочего определения в нашем исследовании была принята дефиниция А.В. Хуторского: «учебно-познавательная компетенция – это ключевая компетенция, направленная на приращение знаний, освоение методов познавательной деятельности, развитие определенных умений и навыков в образовательной деятельности, развитие творческого мышления и самостоятельности в учебной деятельности» [10, С.135].

При составлении авторских задач и заданий мы основывались на классификацию задач с краеведческими сюжетами предложенной С.С. Салаватовой и М.Ю. Солощенко [7]. Ниже в качестве примера приведем несколько задач составленных на основе краеведческого материала Якутии, в частности Кобяйского улуса.

I. Задачи, содержание которых знакомит учащихся с отдельными фактами краеведческого характера

Приведенная ниже задача направлена на закрепление понятий «собственная скорость», «движение по течению реки», «движение против течения реки». Формирует умение применять правила нахождения скорости движения по течению и против течения реки, также умения извлечь нужную информацию из текста задачи.

Пример 1. В 1894 г. императором Александром III на реке Лена было одобрено создание пароходной линии по маршруту Усть-Кут–Якутск. К началу открытия пароходства, по Лене и Витиму работали 15 пароходов, среди которых был самый мощный дореволюционный пароход «Святой Иннокентий», названный так в честь первого иркутского архиепископа. Скорость парохода в стоячей воде 18 км/ч. Скорость течения реки Лена 4 км/ч. С какой скоростью будет двигаться пароход по течению реки? Против течения?

Решение: Формулы, необходимые для решения задач на движение:

Поставим в формулы данные задачи и найдем искомые величины: 18 – 4 = 14 км/ч; 18 + 4 = 22 км/ч.

Ответ: по течению – 22 км/ч., против течения – 18 км/ч.

Следующая задача направлена на формирование умения применять формулы зависимости между скоростью, временем и расстоянием.

Пример 2. 8 октября 1925 года британский одноместный истребитель «Сопвич», пилотируемый летчиком П. М. Фадеевым, взлетев с пристани Даркылах города Якутска, совершил посадку в местности Зеленый луг. Расстояние между которыми 10 км. Известно, что максимальная скорость истребителя «Сопвич» достигал 77 км/ч. Определите время полета истребителя, если данное расстояние он пролетел со скоростью 60 км/ч?

Решение: Поставим данные в формулу 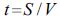. В данной формуле S – это путь, V – скорость, аt – время. Получим: 

Ответ: Данное расстояние истребитель пролетел за 10 минут.

II. Задачи, данные и процесс решения которых ведут к углублению знаний, учащихся по дисциплинам национально-регионального компонента

Задача направлена на закрепление и проверку умения обучающихся решать и оформлять задачи арифметическим способом. Задача развивает умение осуществлять для решения учебных задач операции анализа, синтеза, сравнения.

Пример 3. В 2021 году в Кобяйском улусе селе Сегян-Кюель состоялся двадцатипятилетний юбилейный национальный эвенкийский праздник Бакалдын. В каком году состоится следующий юбилей? Сколько исполнится национальному празднику через 8 лет?

Решение: 1) 2021 – 25 = 1996 – год основания праздника «Бакалдын»; 2) 2030 – 1996 = 34 года.

Ответ: национальному празднику через 8 лет исполнится 34 года.

Задача ниже направлена на формирование умения использовать знаково-символичные средства для решения учебных задач, в частности решать задачи с помощью системы линейных уравнений. Решение задачи способствует овладению действием моделирования.

Пример 4.     Кисломолочный напиток кумыс считается не только компонентом традиционной пищи якутов, но и важной составляющей традиционной культуры народа саха. Якутский кумыс готовится в большом кожаном сосуде «симиир». В двух сосудах симиир 62 л кумыса. После того как из каждого сосуда продали по 10 л кумыса, в одном осталось в 2 раза больше кумыса, чем в другом. Сколько литров кумыса было в каждом сосуде первоначально?

Решение: Пусть x  – количество кумыса в первом сосуде; y  – количество кумыса во втором сосуде. Составим систему уравнений:

Ответ: Первоначально в первом сосуде было 24 литра кумыса, во втором – 38 литра.

III. Задачи, требующие от учащихся закрепления признаков «сквозных понятий» (т.е. понятий, которые вскрываются в процессе изучения различных учебных дисциплин, например оперирование такими понятиями как масштаб, диаграмма, долгота и др.)

Задача знакомит учащихся с понятием «масштаб», с его типами и видами. На примере данной задачи учитель учит определять линейные масштабы карт. Перед началом решения нужно вспомнить географические понятия «протяженность реки», «длина реки». Задача формирует умение устанавливать причинно-следственные связи, делать обобщения, выводы.

Пример 5. На территории Кобяйского улуса протекает множество рек и речек. Среди которых река Лунгха, Лена, Сордонноох и Лабынкыр. Определите протяженность данных рек в километрах, если на карте с масштабом 1:2500000 их длины равны 20,32 см, 176 см, 26,8 см, 16,8 см соответственно. Чему будут равны длины рек на карте с масштабом 1:25000?

Решение: численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе – степень уменьшения проекции. Например, масштаб 1:2500000 показывает, что 1 см на плане соответствует 2500000 см (25000 м или 25 км) на местности. Найдем длину реки Лунгха, для этого 20,32 см нужно умножить на 2500000. Получаем 50800000 см, переводим в километры и получаем 508 км. Длины других рек находятся соответственно.

После решения задачи учащиеся должны ответить на следующий вопрос «Как меняется длина линии на карте при изменении масштаба карты?».

Ответ: 1) 508 км; 4400 км; 670 км; 420 км.; 2) 2 м 3,2 см; 1 м 76 см; 2 м 68 см; 1 м 68 см.

IV. Задачи, выполнение и решение которых требует применения умений и навыков, приобретенных учащимися при изучении различных предметов: работа со статистическим материалом, со справочной литературой, чтение схем, чертежей и диаграмм и др.

На примере следующей задачи вводится понятие столбчатых диаграмм, осуществляется ознакомление с принципом их построения. Задача направлена на формирование умения «читать» и строить столбчатые диаграммы, закрепления у учащихся правила округления натуральных чисел до десятков. Формируется умение понимать информацию, представленную в изобразительной, схематичной, модельной форме.

Пример 6. Приведенные ниже данные округлите до десятков и постройте столбчатую диаграмму: Гора Победа абсолютная высота 3003 м, Мус-Хая (самая высокая вершина горного хребта Сунтар-Хаята) абсолютная высота 2959 м, Малакатын-Тас (гора на юге острова Котельный (Якутия)) абсолютная высота 361 м.

Решение: округлим данные до десятков: 3003 ≈ 3000 м; 2959 ≈ 2960 м; 361 ≈ 360 м. Построим диаграмму:

Рис. 1 – Сттолбчатая диаграмма

VI. Задачи, решение которых дает возможность проводить воспитательную работу, в частности по формированию патриотических качеств личности обучаемых

Задача формирует умение нахождения процентного отношения двух чисел. Важно показать учащимся несколько способов решения задач такого типа. Таким образом, формируется действие выбора наиболее эффективных способов решения задач.

Пример 7. Во время Великой Отечественной войны (1941-1945 гг.) было призвано свыше 62 тысяч якутян. Сколько процентов от общего числа жителей республики было призвано за годы войны, если по данным 1939 г., на территории Якутии проживало 413,8 тысяч человек?

Решение: 1 способ. Задача сводится к определению числа процентов, которое составляет 62 тыс. от 413,8. Примем 413800 человек за 100%. Тогда 4138 человека составляют 1 %, так как 413800:100 = 4138. Определим, сколько-процентов составляют 62000 якутян: 

2 способ. Отношение 62000 к 413800 равно

Ответ: 14,98 %.

Следующие задачи можно использовать при формировании вычислительных умений и навыков быстрого счёта. Задачи способствуют развитию умения выполнять учебно-познавательные действия в умственной форме.

Пример 8. В годы Великой Отечественной войны труженики тыла Якутии приняли активное участие в сборе средств для укрепления оборонной мощи страны. Так, в фонд обороны ими было внесено золотом и серебром 553 кг. Из которых 550 кг серебра. На сколько килограмм меньше собрано золота?

Решение: 1) 553 – 550 = 3 кг золота; 2) 550 – 3 = 547 кг.

Ответ: собрано на 547 кг меньше золота, чем серебра.

Пример 9. Народный писатель Якутии, известный государственный и общественно-политический деятель Андрей Васильевич Кривошапкин родился 17 октября 1940 года в селе Себян-Кюель в семье оленевода. Его известные произведения как «Олени моего детства», «Берег судьбы», «Золотой осень» были написаны в 1985, 1988, 1990 годах. Будучи в каком возрасте А.В. Кривошапкин написал свою повесть «Олени моего детства»?

Решение: 1985 – 1940 = 45 лет.

Ответ: А.В. Кривошапкин повесть «Олени моего детства» написал в возрасте 45 лет.

В процессе исследования проводился педагогический эксперимент на базе МБОУ «Тыайинская СОШ им. Н. Х. Дьяконова» Кобяйского улуса с целью определения эффективности предлагаемой методики. Разработанные нами задачи можно использовать на всех этапах урока и процесса обучения: при изучении нового материала, при усвоении основного материала, при закреплении, применении знаний, в процессе контроля за усвоением знаний.

Как показала апробация, наиболее удачными формами являются: урок-экскурсия, урок-квест, урок-викторина. Они позволяют «погрузиться» учащимся одновременно в предметную и краеведческую тему.

К примеру, при повторении изученного материала учитель на уроках может использовать метод очной или заочной экскурсии по музеям и памятникам родного города или села, где обучающиеся смогут ознакомиться одновременно с историей родного края. Так, учащиеся посетили заочную экскурсию «Площадь Победы» и узнали про историю создания танковой колонны «Советская Якутия» в годы Великой Отечественной войны.

По итогам экскурсии школьникам была предложена следующая задача: «В годы Великой Отечественной войны на добровольные пожертвования трудящихся республики для действующей Красной Армии с января 1943 г. для создания танковой колонны «Советская Якутия» было собрано 5 млн. тыс. руб., а для второй танковой колонны под этим же названием – 10 млн. руб. Танки были переданы войскам 1-го Украинского фронта. Всего сколько средств было собрано в годы войны?».

На уроке-викторине учитель знакомит учащихся с шерстистым мамонтом. Этот вид – вид северных мамонтов, обитавших в регионах Европы, Азии и Северной Америки во времена ледникового периода плейстоценовой эпохи от 2,5 миллионов до 4 тысяч лет назад. На территории Якутии были обнаружены значительная часть находок этого животного. После чего учителем проводится конкурс марафон, где учащиеся разделившись на группы отвечают на вопросы. Например, «Сколько весил мамонт?», «Сколько достигал он в высоту?», «Сколько сантиметров толщины мог достигать слой жира у мамонта?» и т.д.

На уроке-квест все участники собираются, делятся на команды по 5-10 человек и выбирают капитана. Цель данного урока найти секретный пакет, с сюрпризом, выполняя задания. Задача может быть следующей: Структура социального положения горожан Якутска по данным переписи 1923 г. была следующей: прислуга – 7,2%; служащий – 28,1%; хозяин (горожане с собственным делом – «нэпманы») – 10,3%; помогающие члены семьи – 12%; лица свободных профессий – 0,7%; горожане занятые прочими занятиями – 8,4%. Остальные рабочие. Сколько процентов от всего количества горожан составляли рабочие?

С учетом малокомплектности МБОУ «Тыайинская СОШ им. Н. Х. Дьяконова» и малой наполняемостью классов экспериментальная группа была сформирована из числа учащихся 5-6 классов в количестве 14 человек. Диагностика уровня сформированности учебно-познавательной компетенции учащихся до и после эксперимента проведена посредством теста «Методика изучения уровня сформированности учебно-познавательной компетенции учащихся», предложеной В.А. Кошиной [3].

Для установления совпадений или различий между сформированностью учебно-познавательной компетенции учащихся экспериментальных групп до и после эксперимента сформулированы гипотезы:

H₀: гипотеза о значимости различий: показатели уровня сформированности учебно-познавательной компетенции после проведения эксперимента превышают значения показателей до эксперимента.

H₁: гипотеза об отсутствии различий: показатели уровня сформированности учебно-познавательной компетенции учащихся после проведения эксперимента меньше значений показателей до эксперимента.

Для статистической проверки достоверности различий в уровнях сформированности учебно-познавательной компетенции учащихся использовался Т-критерий Вилкоксона.

Таблица 1 – Результаты экспериментальной работы по формированию учебно-познавательной компетенции учащихся

Уровень сформированности учебно-позавательной компетенции (до эксперимента)	Уровень сформированности учебно-познавательной компетенции (после эксперимента)	Сдвиг (после – до)	Абсолютное значение разности	Ранговый номер разности
15	17	2	2	10,5
6	9	3	3	13,5
12	14	2	2	10,5
3	4	1	1	3,5
6	5	-1	1	3,5
10	12	2	2	10,5
10	11	1	1	3,5
7	7	0	0	0
11	12	1	1	3,5
6	4	-2	2	10,5
11	14	3	3	13,5
12	13	1	1	3,5
5	4	-1	1	3,5
16	17	1	1	3,5

Результат: Т_эмп=∑Rt=17,5. При n=13 (с исключением нулевого сдвига) для p≤0.05 Tкр =21. Следовательно, T_кр=21>17,5=Т_эмп , а значит различия в уровне сформированности учебно-познавательной компетенции учащихся можно считать существенным.

Заключение

В целом как показал анализ экспериментальных данных, наблюдается рост уровня сформированности учебно-познавательных компетенций учащихся. Полученные результаты позволили сделать вывод, о том, что предлагаемые нами методические материалы достаточно эффективны и способствуют развитию личности школьника, его интеллектуальных и творческих способностей, ценностных ориентаций.

Таким образом, использование подходящего местного краеведческого материала на уроках математики способствует формированию у обучающихся способности к математическому познанию объектов и явлений окружающего мира и применению математических знаний на практике.

Конфликт интересов  Не указан.

Conflict of Interest  None declared.