DEVELOPMENT OF IMAGINATION, «SPATIAL VISION», «SPATIAL AWARENESS» IN THE PROCESS OF STUDYING THE GEOMETRY COMPONENT IN ELEMENTARY SCHOOL

РАЗВИТИЕ ВООБРАЖЕНИЯ, «ПРОСТРАНСТВЕННОГО ВИДЕНИЯ», «ПРОСТРАНСТВЕННОГО ВООБРАЖЕНИЯ» В ПРОЦЕССЕ ИЗУЧЕНИЯ ГЕОМЕТРИЧЕСКОЙ СОСТАВЛЯЮЩЕЙ В НАЧАЛЬНОЙ ШКОЛЕ

Научная статья

Трофименко Ю.В.*

Ростовский государственный экономический университет, Таганрог, Россия

* Корреспондирующий автор (jultro[at]rambler.ru)

Аннотация

В статье исследованы ключевые противоречия при формировании первоначальных геометрических представлений младших школьников. Исследованы вопросы психолого-педагогических подходов к развитию воображения обучающихся начальных классов. Приводятся обоснования абстрактности изучаемых геометрических понятий. Показана методическая реализация фрагментов деятельности учителя начальных классов по формированию понятий точка, линия, кривая, прямая как абстрактных понятий, отражающих реальную действительность. В ходе исследования, устанавливается, что на первом этапе младшие школьники знакомятся с основными геометрическими фигурами и их свойствами; на втором, на основе предметных действий с моделями геометрических фигур, делают выводы об их свойствах и выполняют элементарные построения; на третьем – обобщают полученный опыт и на его основе учатся абстрагированию и анализу, что влечет за собой развитие пространственного воображения.

Ключевые слова: воображение, геометрические понятия, точка, прямая, кривая, младшие школьники, обучение, начальная школа.

DEVELOPMENT OF IMAGINATION, «SPATIAL VISION», «SPATIAL AWARENESS» IN THE PROCESS OF STUDYING THE GEOMETRY COMPONENT IN ELEMENTARY SCHOOL

Research article

Trofimenko Y.V.*

Rostov State University of Economics, Taganrog, Russia

* Corresponding author (jultro[at]rambler.ru)

Abstract

The article examines the key contradictions in the formation of the initial concepts of geometry among elementary school children. The issues of psychological and pedagogical approaches to the development of imagination of primary school students are researched. The substantiation of the abstractness of the studied geometric concepts is presented. The methodical implementation of fragments of the primary school teacher's activity on the forming the concepts of point, line, curve, straight line as abstract concepts reflecting objective reality is shown. Over the course of the study, it is established that at the first stage, primary school children get acquainted with the basic geometric figures and their characteristics; at the second, on the basis of subject actions with models of geometric shapes, draw conclusions about their features and make elementary constructions; at the third, generalize the experience and on its basis learn abstraction and analysis, which entails the development of spatial imagination.

Keywords: imagination, geometric concepts, point, straight line, curve, elementary school students, education, elementary school.

Воображение представляет собой психический процесс создания новых образов на основе ранее воспринятых. Воображение – это отражение реальной действительности в новых непривычных сочетаниях и связях, оно занимает промежуточное положение между восприятием и мышлением, мышлением и памятью. Психологи утверждают, что воображение одно из самых загадочных психических явлений, механизмы которого еще не изучены [1, С. 55]. Формирование у младших школьников пространственного воображения – одна из главных опор мышления, поскольку внутренние образы, их содержание служат базой умственных действий, которые лежат в основе психических процессов, начиная от простого воспоминания до абстрактного рассуждения. Воображение присуще только человеку, оно позволяет ему выйти за пределы реального мира во времени и пространстве, оно дает возможность человеку в практической деятельности, осознав, представить готовый результат труда. Известно, что материальная и духовная культура человека является продуктом воображения и творчества. Психологи различают активное и пассивное воображение. Активное воображение может быть творческим, продуктивным и воссоздающим (репродуктивным) [2, С. 41]. Активное воображение характеризуется тем, что, пользуясь им, человек по собственному желанию, усилием воли вызывает у себя соответствующие образы. Творческое активное воображение, возникающее в процессе учебной деятельности, предполагает самостоятельное создание образов, которые реализуются в продуктах деятельности. Творческое воображение, как правило, развито у креативных людей: ученых, художников, музыкантов, инженеров и т.д. Воссоздающее активное воображение способствует созданию различных образов, событий, фактов, явлений, которые соответствуют реальной действительности, им пользуются при чтении литературы, изучении топографических карт, чертежей, решении логических и практических задач. Пассивное воображение характеризуется созданием образов, которые не воплощаются в жизнь.

Воображение связано с мышлением, поскольку воображение и мышление возникает тогда, когда необходимо найти новое решение гипотезы, догадки, мысленно представить научные эксперименты, искать и находить решения конкретной проблемы. В математике, например, доказательство различных теорем начинается со слов: «Допустим, что...», «представим себе, что...», то есть процесс математического доказательства начинается с творческого представления или воображения [3, С. 187].

В психологии и нейрофизиологии были получены данные о работе зрительного аппарата человека, роли полушарий головного мозга в опознании зрительных образов, которые приблизили разгадку феномена «видеть» и привели к необходимости пересмотра представлений дидактики о формировании пространственного воображения. В результате исследований установлено, что, рассматривая (оглядывая) предмет, глаз человека не обводит контуры предмета, а совершает сложные движения, имеющие, на первый взгляд, хаотический характер. Феномен «видеть», умение человека «видеть» прошло определенный путь эволюции, в котором выделяются процессы биологического развития органа зрения человека, развития исторического опыта видения и индивидуального развития мышления человека. В процессе видения главным является не то что механически воспринимает наш глаз, а то, что осознает человек в ходе и результате этого процесса. Опыт видения характеризуется такими стадиями:

1) контурное видение;

2) силуэтное видение;

3) объемное видение;

4) светотеневое видение;

5) подвижное видение;

6) аккомодационное видение.

Это нарастание сопровождается расширением объема математических знаний, повышением графической культуры. Не менее важное значение для феномена видеть имеет индивидуальный опыт, который приобретается в процессе развития мышления ребенка, в частности, в период обучения в школе. Путь эволюционного «дозревания» опыта видения находит отражение и в познании ребенком окружающего пространства, и в его собственной деятельности (например, в рисовании), в его мышлении [4, С. 35]. Детское рисование – это индивидуальное спонтанное нарастание графической культуры. Оно должно активно использоваться в процессе обучения математике и служить, таким образом, опорой математического образования обучающихся. Пространство, окружающая среда, интеллектуальное окружение оказывают существенное благотворное влияние на умение человека «видеть», на формирование у него представлений и понятий. Так, Ж. Пиаже, рассматривает мыслительные операции как основную составляющую математического мышления, что оказывает позитивное влияние на формирование, в частности, геометрических представлений и понятий [5, С. 21]. Геометрические представления и понятия связаны с пространственными отношениями, а их усвоение – с особенностями локального восприятия, интерпретации выделенных черт объекта в контексте целостного объекта, так называемого глобального восприятия. Большое значение в процессе формирования геометрических представлений и понятий имеет база наглядных представлений обучающихся, которая изменяется с возрастом и, которая носит индивидуальный характер, о чем свидетельствуют исследования И.С. Якиманской [6, С. 18]. Геометрия как учебный предмет обладает большим потенциалом для развития образной и логической составляющих мышления, для гармонизации деятельности полушарий головного мозга. Устанавливая цели обучения геометрии в начальной школе, следует обращать внимание на создание возможностей приобретения геометрического опыта. Геометрическая деятельность младших школьников должна быть организована таким образом, чтобы познание ими геометрических объектов требовало не только участия зрения и слуха, но и осязания, работы рук, работы мысли. Открытие асимметрии полушарий головного мозга сделало необходимым перенесение в обучении акцентов на формирование образного мышления обучающихся, что подчеркивает актуальность выделения «линии воображения» в методической системе школьного математического образования [7, С. 44–5].

Анализ существующих образовательных УМК позволил выделить противоречия между:

– приоритетом развития пространственных представлений, пространственного воображения, означенных в Примерной программе начального общего образования в одном ряду с развитием исследовательских способностей и логического мышления в процессе изучения элементов геометрии и недостаточным уровнем развития пространственного воображения, овладения обучающимися приемами абстрагирования, анализа, синтеза, классификации и др. для решения математических задач;

– необходимостью развития пространственного воображения и отсутствием доступного учителю систематического дидактически обработанного материала, направленного на развитие пространственного воображения обучающихся.

Означенные положения свидетельствуют об отсутствии целостного осмысления проблемы развития пространственного воображения, пространственного видения младшими школьниками объектов реального мира в процессе изучения геометрической составляющей.

Феномену «видеть», «линии воображения» значительное внимание уделяет и философия математики. В современных направлениях философии математики, интуиция рассматривается как форма видения «в сознании». В дидактике соответствующие исследования рассматривают функции интуиции в разнообразных аспектах, и характеризуют ее (интуицию), как источник идей и гипотез, как генератор образов, схем и других визуализаций математического содержания; как «акселератор» математического мышления, которое направляет и стимулирует дедукцию. Интуиция всегда является потенциальным источником познавательного контакта между представлениями об объекте и его реальным существованием. Многие выдающиеся математики и дидакты математики понятие интуиции отождествляют с понятием воображения, в том числе пространственного, геометрического воображения [8, С. 47].

Для пространственного воображения, в процессе психического развития (языка, мышления, свободного «бега воображения») воображение конкретных понятий или явлений уступает место воображению (зрительному, чаще слуховому) слов как представителей понятий. Пространственное воображение понимается как способность человека к деятельному конструированию и реконструированию образов, которые являются отражением линейных, плоских и пространственных форм реальной действительности [9, С. 17]. Пространственное воображение связано с физическим пространством, оно способствует «изучению» объектов и отношений этого пространства геометрическими и математическими средствами, используя понятия, утверждения, методы, язык, которые являются производными по отношению к физическому пространству, но используются для математического, в частности, геометрического моделирования.

С точки зрения дидактики математики, в частности, практики обучения младших школьников, нас интересует не только пространственное воображение и его применение, но и формирование пространственного воображения в процессе обучения математике. Использование пространственного воображения в учебном процессе понимается как конструирование и реконструирование изучаемых образов реальных объектов, как выполнение с ними некоторых мыслительных операций, связанных с физическим и с геометрическим «оглядыванием» этих образов, заключающихся в: оценке величины образов или реального объекта (абсолютной и относительной); пространственном упорядочении; различении предметов и явлений с точки зрения их геометрических свойств, их положения в пространстве; определение составляющих элементов, сходства и различий между предметами и явлениями окружающего пространства; практическом рассуждении на основе структуры и аналогий; описании вида некоторых разверток; представлении об инвариантности или неинвариантности некоторых их свойств в результате гипотетического преобразования. Такое понимание пространственного воображения следует отличать от понятия геометрического воображения. Геометрическое воображение понимается как способность геометрического моделирования в других разделах математики («геометрического видения»), ведущего к созданию собственных точных образов абстрактных геометрических объектов без опоры на физическое пространство. Разделение понятий пространственного воображения и геометрического воображения обучающихся имеет предметный характер. Физическое пространство на некотором этапе математического образования подвергается «исследованию» в форме абстрагированного от него идеального геометрического пространства. При этом происходит разделение феноменов «видеть» и «знать». Практика работы в школе показывает, что «знать» связано со знанием различных деталей объекта изучения, однако, феномен «знать» не связан с усвоением сформированных и функционирующих онтологических связей. В дидактическом аспекте феномена «видеть» в процессе обучения математике и, в частности, геометрии, возникает необходимость решения многочисленных проблем (например, разработка концепции курса школьной геометрии, методов формирования и развития пространственного воображения в процессе обучения геометрии). Возникает дилемма, на которую указывал А.Д. Александров. Что первично? Интуиция и воображение или строгость и формализм в геометрии и ее преподавании? Геометрия как наука разрешила эту дилемму не выбором одной из указанных альтернатив, а их соединением. Особое значение «геометрическому воображению» или «геометрической интуиции» уделял в своих работах А.Н. Колмогоров, характеризуя их как элемент системы, составляющей математические способности [10, С. 18].

Важная роль в решении соответствующих проблем принадлежит также учителю начальной школы, учителю математики. В результате их активной работы пространственное воображение обучающихся, которое формируется, развивается и совершенствуется, становится существенной структурной компонентой познавательной деятельности обучающихся. Постепенное формирование пространственного воображения расширяет круг интеллектуальных способностей учеников, является адаптивным фактором для подготовки их к использованию в повседневной жизни полученных знаний. Развитие пространственного воображения представляет собой такой характер мыслительной деятельности, как создание образа; оперирование созданным образом в односложных связях и в измененных условиях; творческое конструирование образов; как процесс качественных изменений, характеризующихся элементарным, фрагментарным, статично-динамическим, динамическим и творческим уровнями процесса познания.

Не случайно, поэтому в настоящее время проблеме развития воображения, пространственного воображения, уделяется серьезное внимание. Отметим, что в основе формирования геометрических представлений лежит воображение, пространственное видение. Покажем реализацию развития пространственного воображения, пространственного мышления в практике работы учителей начальной школы, приведя в качестве примеров систему заданий по формированию представлений о точке, видах линий.

Младшим школьникам не скажешь, что «точка есть то часть чего есть – ничто» (Эвклид III в. до н.э.). Представление о точке формируется на основе практических действий.

– Возьмите лист бумаги, проколите его острием карандаша. Мы получили модель, образ точки. Поставьте точку на листе бумаги карандашом, на доске мелом (выполняют). Изображение точки – это видимый след от прикосновения остро оточенного карандаша или другого предмета (мела, фломастера).

– Приведите примеры окружающей действительности, дающие представления о точке. (– Капелька дождя, звезды, видимые ночью с Земли, дают представления о точке. Например, планеты Марс, Венера и др.).

– О звездах космического пространства, видимых с Земли, можно говорить как о точке. На самом деле, звезды, видимые с Земли как точки, представляют собой огромные по величине космические объекты.

– Закройте глаза, представьте, что вы наблюдаете за летящим самолетом, который оставляет след. Зафиксируйте в своем сознании, в своем воображении след летящего самолета, перенесите след летящего самолета на лист бумаги (выполняют).

– Вы когда-нибудь бросали камешки в речку, море? Зафиксируйте в своем сознании след «бегущего» по волнам камешка. Перенесите, зафиксированный в своем воображении след, бегущего по волнам, камешка на лист бумаги, доски (выполняют).

– Представьте камень, падающий с крыши. Перенесите след камня, падающего с крыши, на лист бумаги (выполняют). На доске и в тетрадях получились фигуры (рис. 1).

Рис. 1 – Образы линий

– Посмотрите внимательно, что мы получили? (– Это линии.)

В природе линии, как таковые, не существуют, они существуют в нашем воображении. Мы можем в реальной жизни видеть, представлять только образы, модели этих линий.

– Какие это линии? (– Кривые, прямые, волнистые.)

– В математике такие объекты называют геометрическими фигурами: прямыми и кривыми линиями. Посмотрите в окно. Вы видите провисшие провода, представление, о каких линиях дают провисшие провода? (– О кривых линиях.)

– А туго натянутая веревка, нить? (– О прямой линии.)

Учитель констатирует: «В математике для линий (прямой, кривой), как и для точки не существует определения, мы можем отличать их друг от друга только по набору существенных свойств, одни из которых устанавливаем путем воображения, другие экспериментально, выполнив практическую работу.

Учитель предлагает паре учеников туго натянуть нить, концы нити прячутся от взгляда обучающихся. Каким инструментом нужно воспользоваться, чтобы получить на листе бумаги прямую линию. (– Линейкой.)

– Подумайте, как получить представление о прямой линии без помощи линейки? (– Нужно согнуть лист бумаги.)

 

∙

∙

– Согните лист бумаги (выполняют). Линия сгиба листа бумаги дает представление о прямой линии. Отметьте на линии сгиба две точки, приложите линейку к линии сгиба и проведите линию по линейке. Укажите на прямой две точки, обозначив их латинскими буквами А и В (выполняют), рис. 2.

В

А

 

 

Рис. 2 – Прямая линия с двумя точками

– Прямую линию обозначают любыми точками, лежащими на ней. Читают: прямая АВ или прямая ВА. Попытайтесь через эти же две точки провести другую прямую линию. (– Не получается.)

Учитель констатирует: «Через две точки можно провести только одну прямую линию. Это первое свойство прямой линии, с которым мы познакомились практически».

– Теперь попытайтесь продолжить прямую АВ вправо и влево как угодно далеко. (– Не хватает места в тетради.)

– На рисунке мы можем изобразить только часть прямой линии, а всю линию изобразить нельзя. В математике говорят, что прямая линия бесконечна, она не имеет начала и не имеет конца. Ее нельзя измерить, длину линии нельзя выразить числом. Бесконечность линии – это второе свойство прямой линии, в котором вы убедились опытным путем.

– Поставьте точку А в тетради (учитель выполняет эту работу на доске), проведите через нее несколько различных прямых линий (рис. 3). В геометрии место, где пересекаются прямые линии, называют точкой их пересечения.

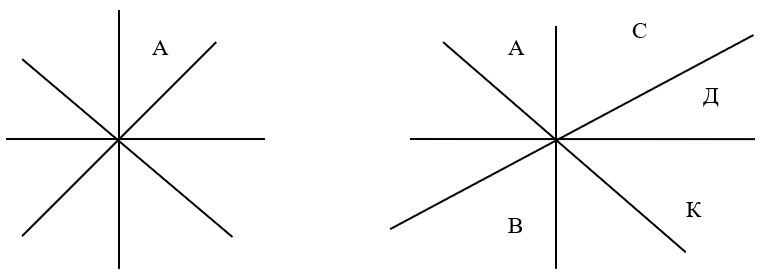
Рис. 3 – Пересечение прямых

Все линии (рис. 3) имеют разное направление (горизонтальное, вертикальное, наклонное). Сколько точек нужно отметить, чтобы через них можно было провести линию нужного направления? Объясните, почему? (– Каждая прямая линия определяется двумя точками. Линий всего 4. Значит, чтобы каждая линия имела свое направление и название, нужно отметить 4 точки.)

– Поставьте точки, назовите и запишите образовавшиеся линии. Выполняют (рис. 3). Читают: прямая АВ, АС, АД, АК или ВА, СА, ДА, КА.

Абстрактное понятие прямой, таким образом, наделяется рядом конкретных свойств:

1. Для построения прямой пользуются линейкой или предметом с идеально ровными краями (является обобщением опыта работы).

2. У прямой линии нет начала и нет конца – она бесконечна (это свойство выделено после эксперимента)

3. Прямая линия однозначно задается двумя точками (проанализировано и аргументировано учащимися в соответствии с рисунком 3).

На этапе закрепления темы полезно выполнить несколько нестандартных заданий:

1. Будет ли точка пересечения у прямых линий, если это железнодорожные или трамвайные рельсы, или края линейки и др.?

2. Может ли у двух пересекающихся прямых быть две точки пересечения? Поясните.

3. Будут ли прямые АВ и СД пересекаться (рис. 4). Объясните.

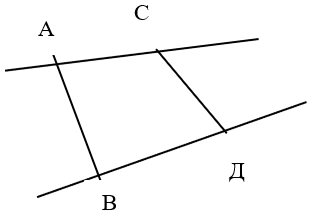
Рис. 4 – Задание для выполнения ученикам

Выполнение задания требует анализа рисунка и аргументированного вывода, типа: поскольку прямые линии бесконечны, то их можно продолжить как угодно далеко вверх и вниз. Очевидно, что, продолжив прямые АВ и СД, они пересекутся в одной точке.

Предложенные задания являются абстрактными, они активизируют образное и логическое мышление. Их выполнение способствует закреплению знаний о прямой линии как абстрактного понятия. Задания такого характера выполняются под наблюдением учителя, который следит за ходом рассуждений учащихся, и по мере необходимости корректирует их. Такой подход к процессу развития пространственного воображения, позволяет каждому обучающемуся быть активным на уроке.

Итак, на первом этапе младшие школьники знакомятся с основными геометрическими фигурами и их свойствами; на втором, на основе предметных действий с моделями геометрических фигур, делают выводы об их свойствах и выполняют элементарные построения; на третьем – обобщают полученный опыт и на его основе учатся абстрагированию и анализу.

Таким образом, у учителя начальной школы имеются потенциальные возможности для развития у младших школьников воображения, «пространственного видения», пространственного воображения в процессе изучения геометрической и не только геометрической составляющей. Учителю для реализации означенных задач, необходимо тщательно готовиться к уроку по какой бы из существующих УМК он не работал.

Конфликт интересов  Не указан.

Conflict of Interest  None declared.