MAGNETIC FLOW AND INDUCTION IN THE HEARTS OF MAGNETIZABLE BALL CHAINS

МАГНИТНЫЙ ПОТОК И ИНДУКЦИЯ В СЕРДЦЕВИНАХ НАМАГНИЧИВАЕМЫХ ЦЕПОЧЕК ШАРОВ

Научная статья

Сандуляк А.В.¹, Горпиненко Ю.О.², Полисмакова М.Н.³*, Сандуляк Д.А.⁴, Сандуляк А.А.⁵

¹ ORCID: 0000-0001-7605-2702;

³ ORCID: 0000-0002-4564-6206;

⁴ ORCID: 0000-0003-4269-6133;

⁵ ORCID: 0000-0002-5111-6092;

^{1, 2, 3, 4, 5} МИРЭА – Российский технологический университет, Москва, Россия

* Корреспондирующий автор (m.polismakova[at]mail.ru)

Аннотация

Изложены результаты экспериментальных исследований цепочек шаров в магнитном поле длинного соленоида – при различных значениях напряженности намагничивающего поля H = 4,8-54,5кА/м и числа шаров n = 2-14 в цепочке: с шарами радиусом R = 15мм, а также с шарами радиусом R = 20мм. Вместо традиционных измерительных датчиков в виде круговых петель из провода (подключаемых к микровеберметру) применены аналогичные по принципу, но более технологичные датчики, выполненные в виде круговых контуров разного относительного радиуса r/R = 0,2-0,9 – на печатных платах, помещаемых между смежными шарами в средней части цепочки. Получены семейства (по r/R и n) полевых зависимостей магнитного потока Ф сквозь эти датчики, а также соответствующие семейства полевых зависимостей магнитной индукции B в каждой (по r/R) условной сердцевине цепочки шаров. Установлен регрессирующий (но без признаков приближающего насыщения) рост полевых зависимостей Ф и B. Показано, что при увеличении r/R, т.е. по мере «утолщения» условных сердцевин, несмотря на увеличение значений Ф, значения B снижаются – ввиду уменьшения объема металла в сердцевине. Выявлено, что цепочки, характеризующиеся относительно малыми значениями n, по всем сердцевинным значениям Ф и B уступают более длинным цепочкам: из-за большего проявления размагничивающего фактора «коротких» цепочек шаров; значения Ф и B стабилизируются (достигая области автомодельности) при n = 10-12, причем независимо от R. На примере зависимостей B от r/R и n для цепочек с шарами R = 15мм и цепочек с шарами R = 20мм (взаимно согласующихся) показана универсальность этих зависимостей для подобного рода магнетиков.

Ключевые слова: намагничиваемая цепочка шаров, относительный радиус ее условной сердцевины, датчик-контур на печатной плате, магнитный поток, магнитная индукция.

MAGNETIC FLOW AND INDUCTION IN THE HEARTS OF MAGNETIZABLE BALL CHAINS

Research article

Sandulyak A.V.¹, Gorpinenko Yu.O.², Polismakova M.N.^3,*, Sandulyak D.A.⁴, Sandulyak A.A.⁵

¹ ORCID: 0000-0001-7605-2702;

³ ORCID: 0000-0002-4564-6206;

⁴ ORCID: 0000-0003-4269-6133;

⁵ ORCID: 0000-0002-5111-6092;

^{1, 2, 3, 4, 5} Russian Technological University (MIREA), Moscow, Russia

* Correspondent author (m.polismakova[at]mail.ru)

Abstract

The article contains the results of experimental studies of ball chains in the magnetic field of a long solenoid for different values of the magnetizing field strength H = 4.8-54.5 kA/m and the number of balls n = 2-14 in the chain: with balls of radius R = 15 mm, as well as with balls of radius R = 20 mm. Instead of traditional measuring sensors in the form of circular loops from a wire (connected to a micro-webermeter), similar but more technologically advanced sensors made in the form of circular loops of different relative radii r/R = 0.2-0.9 are used on printed circuit boards between adjacent balls in the middle of the chain. The families (in r/R and n) of field dependences of the magnetic flux Φ through these sensors are obtained, as well as the corresponding families of field dependences of the magnetic induction B in each (in r/R) conditional core of the ball chain. A regressive (but without the signs of approaching saturation) growth of the field dependences Φ and B was established. It is shown that with increasing r/R, i.e., as the conditional cores “thicken” despite the increase in Φ values, B values decrease due to a decline in the volume of metal in the core. It was revealed that chains characterized by relatively small values of n are inferior to longer chains in all core values of Ф and B: due to the greater manifestation of the demagnetizing factor of “short” ball chains; the values of Ф and B are stabilized (reaching self-similarity region) at n = 10-12, and independently of R. The universality of these dependences for this kind of magnets is shown on the example of the dependences of B on r/R and n for chains with balls R = 15 mm and chains with balls R = 20 mm (mutually consistent).

Keywords: magnetizable ball chain, relative radius of its conditional core, sensor circuit on a printed circuit board, magnetic flux, magnetic induction.

Введение

Изучение магнитных свойств неоднородных, в частности, сыпучих (гранулированных [1], [2], [3], зернистых [4], [5] и порошковых [6], [7], [8]) сред сводится, как правило, к так называемой макромодели эффективной среды [5], когда используемый образец сыпучей среды уподобляется квазисплошному магнетику, характеризующемуся определенными общими (как для сплошного магнетика) свойствами. Однако наряду с этим самостоятельный интерес представляет изучение таких специфичных сред на уровне как бы «микромодели» – с углублением представлений о ряде магнитных параметров именно внутри такого рода магнетиков, в том числе между самими элементами (гранулами), что требует соответствующей диагностики (реализация которой в микрообъемах, как известно, сопряжена с определенными сложностями). Между тем, именно такая информация крайне необходима, в частности, для результативного решения задач фильтрационной магнитной сепарации [1], когда в качестве рабочего органа (фильтр-матрицы) используются намагничиваемые гранулированные среды.

Если исходить из структурных особенностей гранулированных сред, то с точки зрения их намагничивания заслуживают особого внимания ключевые здесь компоненты этих структур – прямые и извилистые цепочки гранул (всегда проявляющие себя в направлении намагничивания), выполняющие функцию «проводников» магнитного потока, ответственных за намагничивание таких сред в целом [1], [9], [11]. Согласно разработанной в [1], [9], [11] модели избирательного (поканального) намагничивания гранулированной среды, концептуальными в этой модели являются такие параметры как магнитная проницаемость той или иной сердцевины радиусом r ≤ R (внутри цепочки шаров радиусом R) и магнитная проницаемость любого из тонких слоев этой, условно представляемой в виде многослойной, сердцевины (вплоть до ее предельного радиуса r → R). Благодаря этому становится возможным получение решений обеих задач. Так, кроме значений макромодельных магнитных параметров гранулированной среды, т.е. среды-«жгута» цепочек гранул (в частности, магнитной проницаемости среды как квазисплошного магнетика и магнитной индукции в нем), можно также определять значения магнитной индукции в разных (по радиусу r) сердцевинах цепочки шаров и тонких слоях этих сердцевин (а это дает основания для определения напряженности поля и его неоднородности непосредственно в порах и пр.) [1], [9], [11].

Конкретизация задач экспериментальных исследований

Разумеется, доказательством состоятельности модели поканального намагничивания гранулированной среды в дополнение к сравнению расчетных и экспериментальных (вполне доступных) данных макромодельных магнитных параметров [1], [9], [10], могли бы послужить, в частности, экспериментальные данные такого ключевого магнитного параметра как магнитная индукция в разных (по радиусу r) сердцевинах цепочки шаров.

Предпринимавшиеся решения этой задачи, которые во многом способствовали созданию и развитию модели поканального намагничивания гранулированной среды, изложены в [1], [9], [11]. Эмпирической базой служили эксперименты [1] по измерению магнитного потока Ф сквозь измерительные, выполненные из тонкого провода, концентричные петли (разного радиуса r ≤ R), подключаемые к микровеберметру и располагаемые между шарами в средней части достаточно длинной цепочки шаров, намагничиваемой в еще более длинном соленоиде.

Такой подход к получению столь необходимых, характеризующих те или иные сердцевины цепочки шаров, экспериментальных данных Ф, являющихся принципиальными (для определения магнитной индукции и проницаемости сердцевин и «слоев» этих сердцевин, а также напряженности поля и его индукции между шарами), следует признать весьма перспективным. При этом измерениями охватывается существенная часть сечения микрообъема между шарами – за счет имеющейся возможности «углубить» измерительные датчики (петли) в изучаемый образец-магнетик, т.е. в цепочку контактирующих шаров, особенно при использовании шаров повышенного радиуса [1], [9], [11]. Так, радиус петли r может варьироваться от значений r, соизмеримых с радиусом шаров, до значений r, отстоящих от точки контакта шаров сравнительно недалеко (пока диаметр провода петли станет соизмеримым с расстоянием между поверхностями смежных шаров).

Вместе с тем, реализация этого подхода была бы более информативной (по сравнению с [1], [9], [11]) при выполнении, в частности, следующих расширенных требований.

Так, придерживаясь того же, наиболее приемлемого здесь варианта датчика (основывающегося на принципе «петли»), необходимо совершенствовать как технологию его изготовления (с обеспечением формы датчика – именно в виде строго плоской окружности, причем для системы разных по радиусу датчиков – и их строгой концентричности), так и технологию оперативного позиционирования датчика (строго в плоскости симметрии межшарового объема, причем при полном совпадении центра окружности датчика и точки контакта шаров).

Далее, необходимо при проведении подобного рода опытов увеличить число разных по радиусу датчиков, т.е. минимизировать шаг радиуса используемых датчиков.

Важным является также проведение экспериментов с использованием изучаемых образцов-цепочек разной длины, в данном случае – разного числа шаров в цепочке, начиная с двух и завершая таким их числом, когда при его дальнейшем увеличении достигалось бы только простое воспроизводство измеряемых данных (что свидетельствовало бы о практическом обнулении размагничивающего фактора такого удлиненного специфичного магнетика).

Кроме того, следовало бы не ограничиваться экспериментами с одинаковыми по диаметру образцами-цепочками, а использовать образцы-цепочки разного диаметра (т.е. с шарами в них одинакового, но иного диаметра).

Результаты экспериментальных исследований и их анализ

При проведении опытов с той или иной цепочкой шаров диаметром D (радиусом R), помещаемой в достаточно длинный секционный соленоид, измеряли магнитный поток Ф датчиками этого потока, размещаемыми между срединными шарами цепочки шаров (рис.1а) – подобно размещению традиционных круговых датчиков-петель (из провода) в ранее выполняемых экспериментах [1], [9], [11].

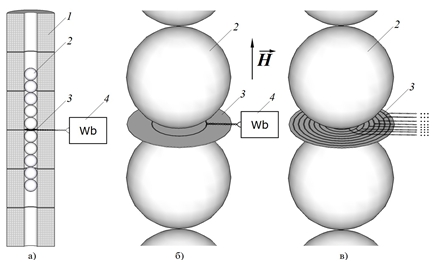
Рис. 1 – Схема экспериментальной установки: 1 – секционный соленоид, 2 – цепочка шаров, 3 – датчик (дополнительно иллюстрируется справа) в виде печатной платы с круговым контуром, имеющим проводные выводы к микровеберметру (или блоком концентричных контуров, каждый из которых имеет проводные выводы к микровеберметру, 4 – микровеберметр

 

Однако в данной работе, в отличие от существующих решений, когда для подобных целей традиционно изготовляются или заимствуются датчики в виде потокоизмерительных петель (обычно из круглого провода), а также катушек, для проведения экспериментов в данной работе изготовлен и протестирован модернизированный датчик. Будучи эквивалентным по принципу традиционным датчикам, он является более технологичным по отношению к ним, особенно если речь идет о его применении для диагностики поля в характерных для рассматриваемой задачи микрообъемах. Это – выполненный на тонкой (0,25мм) печатной плате круговой контур (рис.1б), разумеется, с малым разрывом для проводного соединения соответствующих концов этого контура с микровеберметром, а для большей оперативности (для исключения частых замен датчиков с контурами-петлями иных радиусов) – система концентричных контуров (рис.1в).

При таком техническом решении создаются лучшие, чем в аналоге, возможности для создания требуемой формы датчика (контура-петли) – как практически идеальной окружности на плоскости, а при использовании системы датчиков – их концентричности. К тому же, обеспечиваются также лучшие возможности (причем с упрощением) для позиционирования датчика (системы концентричных контуров-петель) – строго в плоскости симметрии микрообъема между шарами, куда помещается такой датчик (на базе печатной платы). Кроме того, лучшими становятся возможности для выполнения необходимого требования о «совпадении» центра окружности датчика (датчиков) с точкой контакта смежных шаров (т.е. с центром симметрии межшарового объема). Для этого и одновременно для обеспечения взаимного контакта смежных шаров, между которыми размещается датчик, в центре платы, т.е. концентрично контуру-петле (контурам-петлям), выполнено посадочное отверстие, диаметр d₀ которого определяется в зависимости от диаметра D используемых шаров и толщины δ рабочей платы:

    (1)

Это условие следует из несложных геометрических связей, если в звене цепочки шаров, где расположен датчик (рис.2), рассмотреть прямоугольный треугольник (пунктир) между центром шара, характерной точкой кромки отверстия в плате и основанием нормали, проведенной из этой точки к межцентровой линии шаров.

Опыты (с измерением магнитного потока Ф сквозь измерительные датчики: контуры-петли) выполнены при различных значениях напряженности намагничивающего поля H – от 4,8кА/м до 54,5кА/м, числа шаров n в цепочке – от 2 до 14 (соответственно длины цепочки – от 2D до 14D), радиуса датчика r (относительного радиуса r/R) – от 0,2 до 0,9. После каждого измерения Ф проводилось размагничивание изучаемой цепочки шаров (обладающей остаточной намагниченностью) затухающим переменным полем.

 

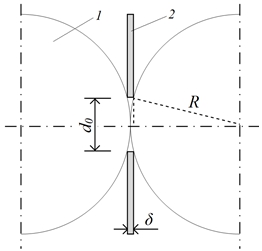
Рис. 2 – Схема звена цепочки шаров 1 (двух срединных) диаметром D=2R, между которыми размещен датчик 2 с толщиной (печатной платы) δ и центральным отверстием диаметром d₀, определяемом согласно условию (1)

 

В опытах использовались цепочки шаров диаметром D=30мм (R=15мм) и дополнительно – цепочки шаров диаметром D=40мм (R=20мм). При этом выбор шаров именно повышенного диаметра (в цепочках шаров повышенного габарита) обусловлен необходимостью «проникновения» датчика (насколько это возможно даже при столь малой толщине датчика) вглубь межшарового объема (рис.2), все более уменьшающегося по «поперечнику» при уменьшении относительного радиуса r/R применяемого датчика.

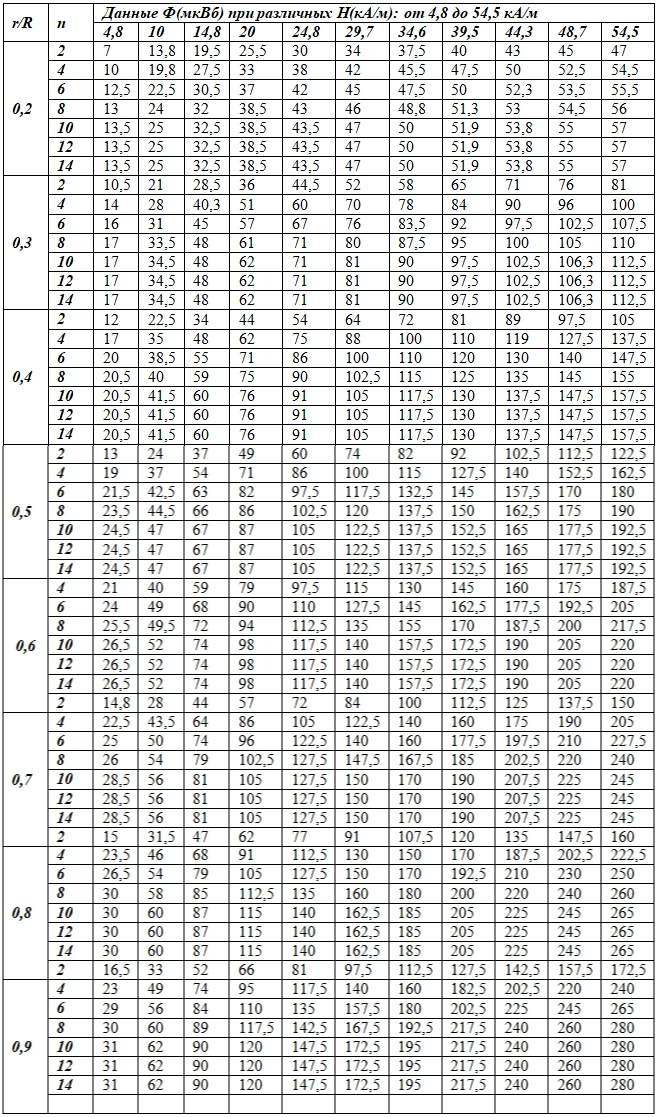
Данные измерений магнитного потока Ф, полученные при различных значениях H, n и r/R (в указанных выше диапазонах варьирования этих параметров), приведены в табл.1 – для цепочек шаров диаметром D =30мм.

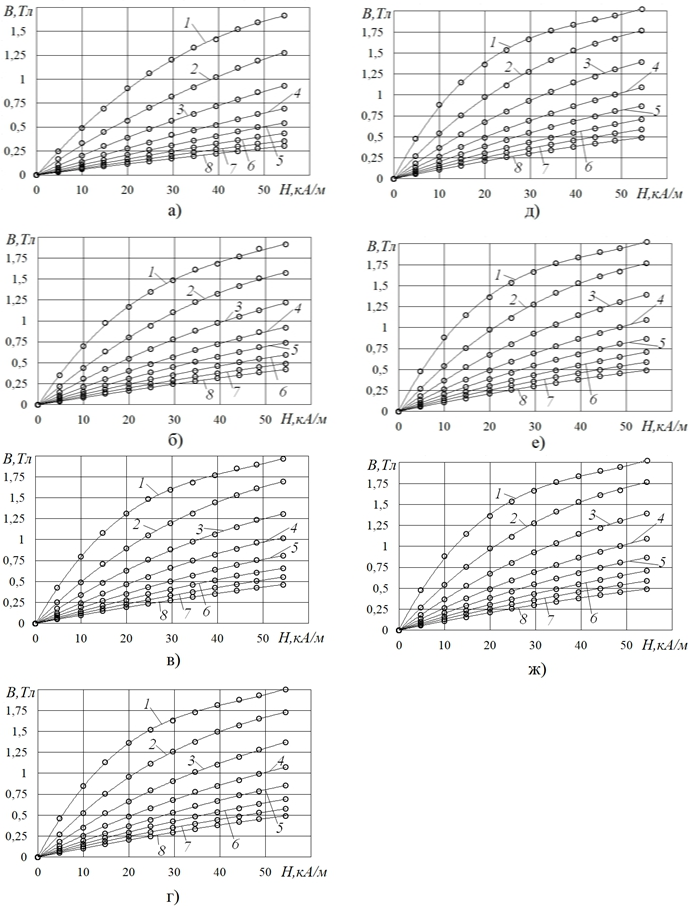
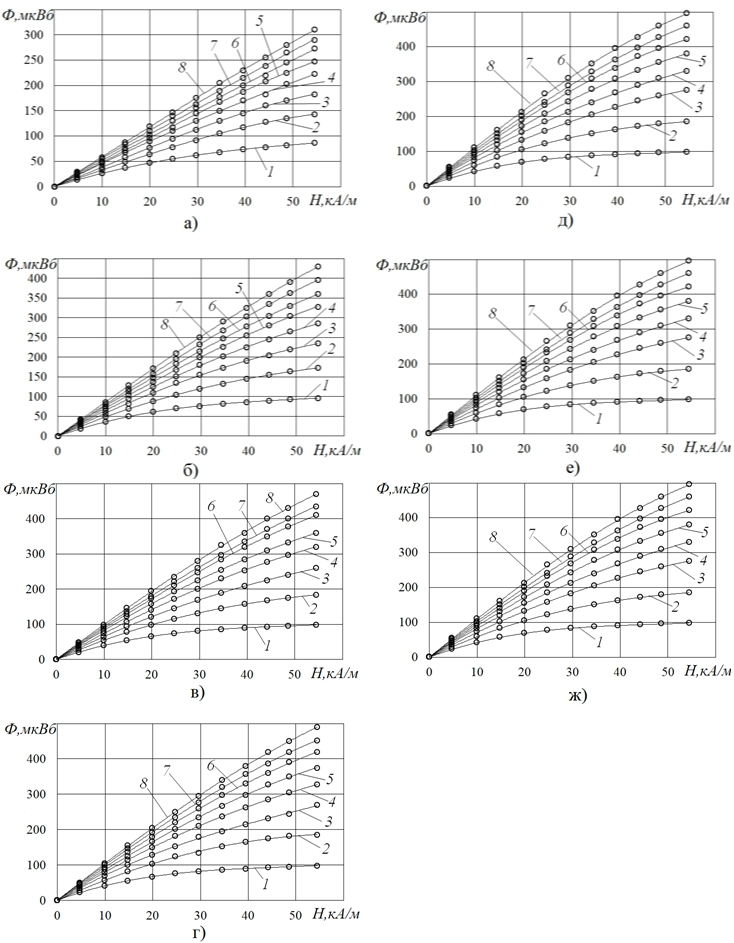
О характере найденных полевых зависимостей Ф, т.е. зависимостей Ф от H, причем в виде весьма представительных семейств таких зависимостей (для различного числа шаров в цепочке n и различного относительного радиуса контуров-петель r/R, т.е. различного относительного радиуса той или иной сердцевины цепочки шаров), можно судить по иллюстрациям на рис.3.

 По всем зависимостям Ф от H полученных семейств видно (рис.3), что с повышением напряженности поля H значения магнитного потока Ф монотонно возрастают, но, заметим – со снижением интенсивности этого роста по мере повышения H. При этом параметры n и r/R, практически не влияя на характер этих зависимостей, тем не менее, оказывают существенное влияние на значения Ф. В частности, чем больше радиус контура r (относительный радиус r/R), тем больше и магнитный поток Ф сквозь него (рис.3), что свидетельствует и о все большем (при повышении r/R) магнитном потоке Ф в соответствующей сердцевине цепочки шаров.

Вместе с тем, если перейти от данных магнитного потока Ф к данным магнитной индукции B (как частное от деления величины Ф на сечение контура-петли S=πr², отражающее поперечное сечение сердцевины того или иного радиуса r), т.е. используя связь:

      (2) то в дополнение к семействам зависимостей Ф от H (рис.3) можно получить родственные им, тоже с регрессирующим ростом, семейства зависимостей B от H (рис.4), где, заметим, взаимное положение соответствующих кривых ожидаемо изменилось на обратное.

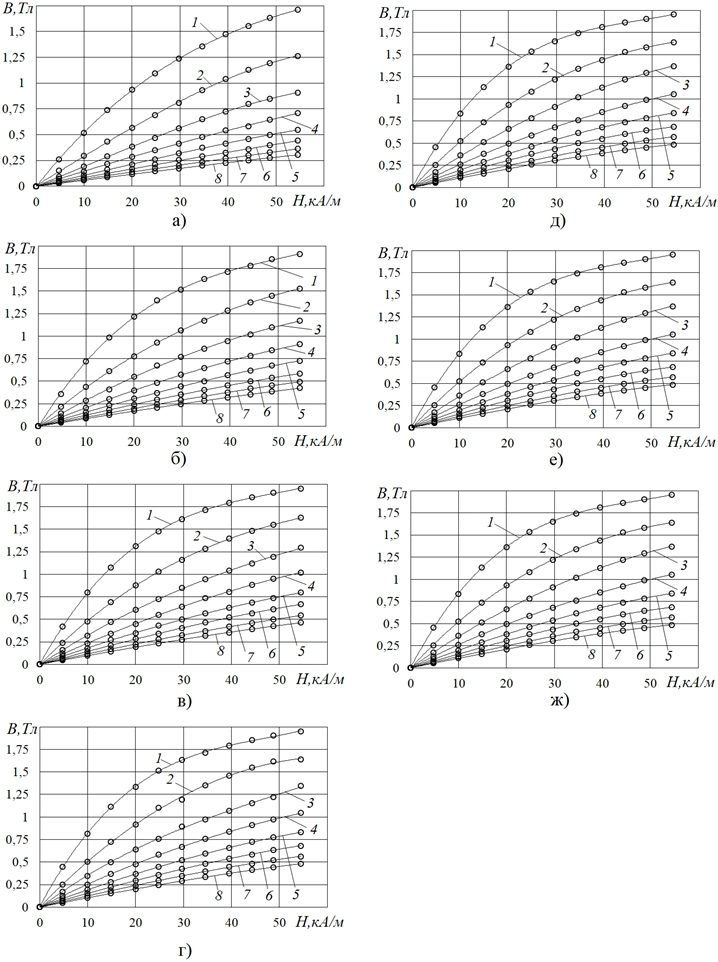
Действительно, показанные на рис.4 кривые B от H – это, по сути, кривые намагничивания сердцевин (того или иного радиуса r) цепочки шаров. Значит, с повышением r, когда объемная доля γ металла в сердцевине уменьшается (рис.5), магнитная индукция в ней снижается (рис.4).

Так, если радиус r сердцевины r/R → 0, т.е. когда «прослойка» между шарами становится исчезающе малой, то объемная доля γ металла в ней: γ → 1. При увеличении же r/R, вплоть до r/R = 1, объемная доля γ металла в ней уменьшается до значения γ = 0,67, как это следует из примера условного звена (длиной 2R) цепочки шаров (рис.5а). Действительно, при такой же длине сердцевины в модуле (2R) ее объем равен πr²2R, а объем металла (как совокупный объем двух полушарий): 4πR³/3. Значит, частное от взаимного деления этих объемов: (4πR³/3)/(πr²2R) = γ =2/3=0,67.

   

Таблица 1 – Магнитный поток Ф, пронизывающий контуры относительного радиуса r/R при числе n шаров в цепочке и напряженности поля H. Диаметр шаров D = 30 мм

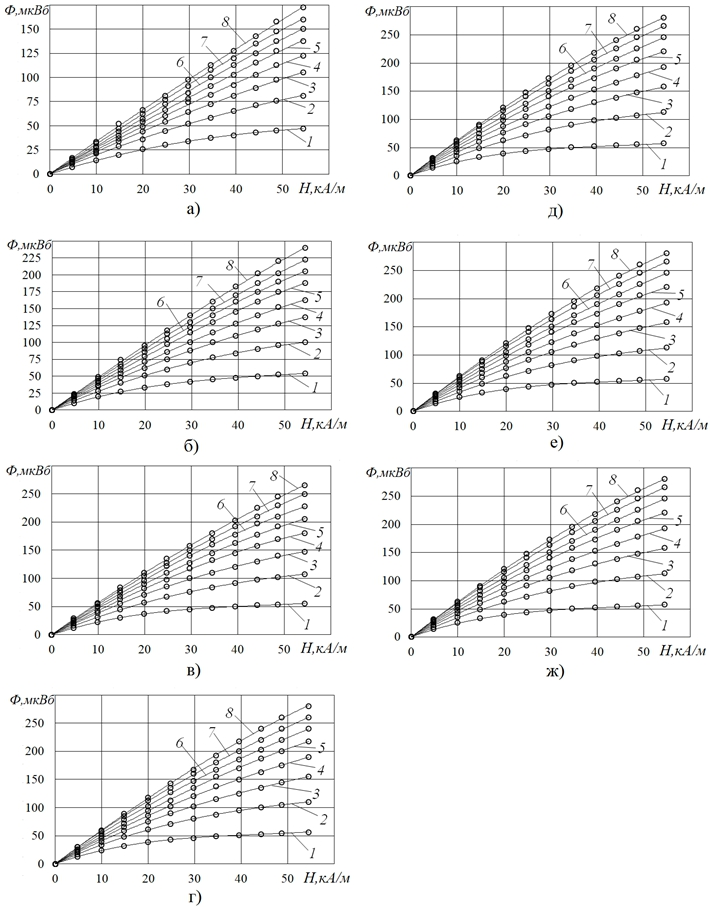Рис. 3 – Полевые зависимости магнитного потока сквозь контуры-петли различного радиуса r (на печатной плате),располагаемые в плоскости симметрии межшарового объема и «охватывающие» точку контакта шаров радиусом R=15мм, для различного числа шаров n в цепочке; а) n=2, б) n=4, в) n=6, г) n=8, д) n=10, е) n=12, ж) n=14; 1– r/R=0,2, 2– r/R=0,3, 3– r/R=0,4, 4– r/R=0,5, 5– r/R=0,6, 6– r/R=0,7, 7– r/R=0,8, 8– r/R=0,9

 

Для определения промежуточных значений γ (при 0 ≤ r/R ≤ 1) следует учесть геометрические особенности сердцевины того же условного звена (рис.5а). Объем металла γ в сердцевине несложно определить, если принять во внимание известное выражение для расчета объема двух шаровых сегментов (как части объема металла сердцевины). Тогда можно показать, что для любого значения r/R в интересующем нас диапазоне 0 ≤ r/R ≤ 1 величина γ может быть определена по выражению:

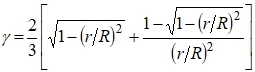     (3) графический вид которой показан на рис. 5б.  

Рис. 4 – Полученные по данным рис.4 полевые зависимости индукции (кривые намагничивания)для сердцевин радиусом r, условно выделяемых в цепочке шаров (R=15мм); обозначения соответствуют обозначениям на рис.3

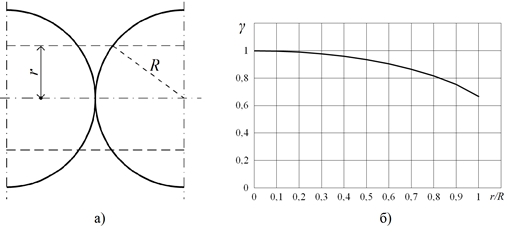
Рис. 5 – Иллюстрация к оценке объемной доли γ металла в сердцевине радиуса r цепочки шаров радиуса R (а) и вид представленной выражением (3) зависимости γ от r/R (б)

Характеризуя показанные на рис.3 и рис.4 зависимости, которые по мере увеличения напряженности поля H демонстрируют, как уже оговорено выше, продолжающийся рост и магнитного потока Ф, и более показательного параметра, а именно индукции B, причем со снижением интенсивности этого роста, следует отметить примечательную особенность этих зависимостей. Так, признаков насыщения той или иной сердцевины или приближения к насыщению (как это обычно наблюдается, например, при изучении магнитных свойств ферромагнитных сплошных образцов) здесь нет.

Еще одной особенностью зависимостей, показанных на рис.3 и рис.4, является то, что на уровень их расположения (по ординатам, т.е. по числовым значениям Ф и B) заметное влияние оказывает число шаров n в цепочке (если сравнивать зависимости, полученные при относительно малых n, т.е. для относительно «коротких» цепочек-образцов, с зависимостями, полученными при повышенных n, т.е. для удлиненных цепочек-образцов).

Сказанное позволяет говорить о проявлении размагничивающего фактора таких специфичных магнетиков. Так, начиная с минимального значения n=2, при последующем увеличении n магнитный поток Ф в каждой из сердцевин цепочки и индукция B в сердцевине повышаются (рис.3,4), свидетельствуя тем самым об уменьшении размагничивающего фактора сердцевин (аналогично традиционным сплошным [12], [13], [14] и даже пористым, в частности, гранулированным [1], [4] образцам).

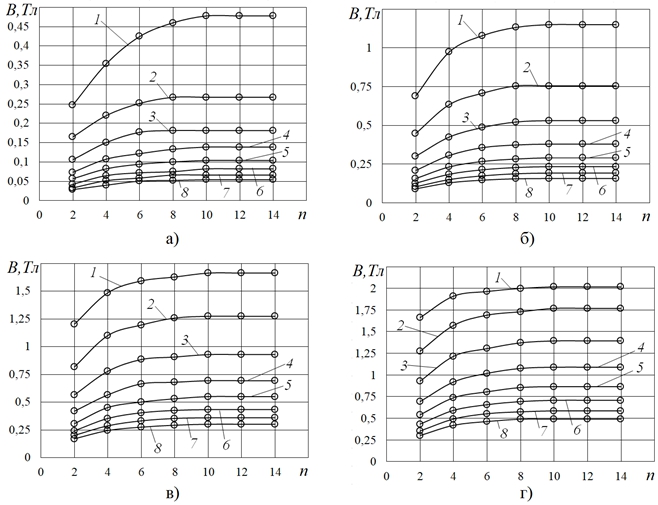
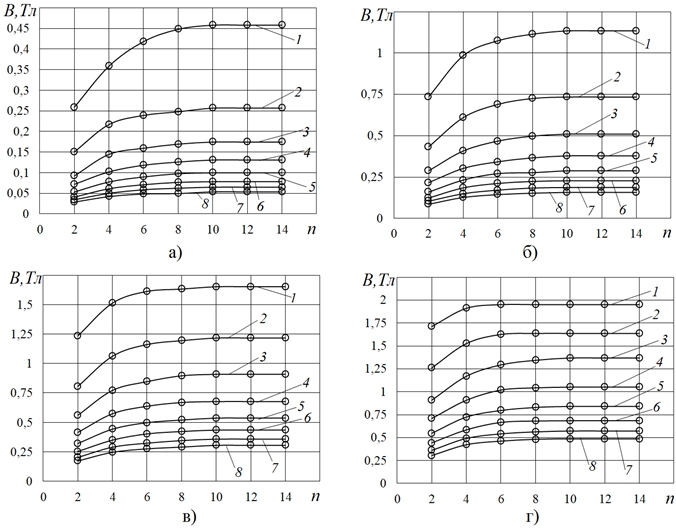
При этом интенсивность «приращения» Ф и B по мере увеличения n снижается (рис.3,4), что более наглядно видно, если показанные, например, на рис.4 данные B от H, полученные при разных значениях n, частично (охватывая, тем не менее, весь используемый диапазон напряженности поля H) представить в координатах B от n (рис.6).

Рис. 6 – Зависимости индукции в сердцевине (радиусом r) цепочки шаров радиусом R =15мм от числа шаров, при различной напряженности поля H; а) H=4,8кА/м, б) H=14,8кА/м, в) H=29,7кА/м, г) H=54,5кА/м; 1– r/R=0,2, 2– r/R=0,3, 3– r/R=0,4, 4– r/R=0,5, 5– r/R=0,6, 6– r/R=0,7, 7– r/R=0,8, 8– r/R=0,9

 

Видно (рис.6), что интенсивность роста B снижается всего лишь до n = 10-12, причем для всех сердцевин (для разных r/R), а при n ≥ 10-12 зависимости B от n становятся практически автомодельными. Это значит, что при n ≥ 10-12 изучаемый образец (напомним, здесь в виде цепочек шаров радиусом R = 15мм) является уже достаточно длинным – настолько, что влияние размагничивающего фактора минимизировано.

Уместно предположить, что такие из полученных результатов как зависимости магнитной индукции B от напряженности поля H (рис.4), а также от числа n шаров в цепочке (рис.6), характеризующие определенные (по относительному радиусу r/R) сердцевины цепочек шаров, согласно принципу подобия (по безразмерным параметрам n и r/R) должны оставаться справедливыми для цепочек шаров иного радиуса, что требует соответствующего экспериментального подтверждения.

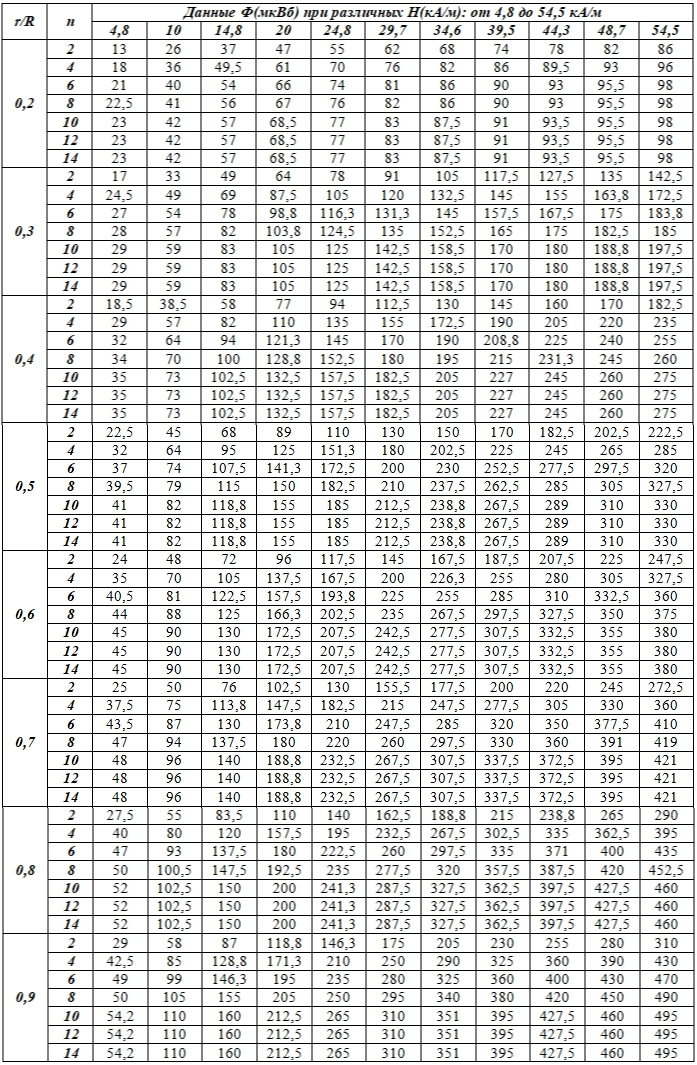
Поэтому в дополнение к приведенным выше данным измерений магнитного потока Ф при тех же значениях напряженности намагничивающего поля H, числа шаров в цепочке n и относительного радиуса контуров-петель (сердцевин цепочек шаров) r/R получены аналогичные данные (табл.2), но для цепочек шаров иного радиуса: R = 20мм. При этом использовался описанный выше датчик с контурами-петлями на печатной плате, но применительно к изменившемуся радиусу шаров.

Представленные для цепочек шаров такого радиуса (R = 20мм) соответствующими зависимостями Ф от H (при различных n и r/R) на рис.7 (как и ранее на рис.3 для цепочек шаров радиусом R = 15мм при тех же n и r/R), они свидетельствуют о качественном согласии сопоставляемых (на рис.7 и на рис.3) зависимостей.

Что же касается последовавших из них (цепочки шаров радиусом R = 20мм) наиболее интересующих нас зависимостей B от H (при различных n и r/R) на рис.8, а также зависимостей B от n (при различных H и r/R) на рис.9, то они свидетельствуют о полном, теперь уже количественном, согласии с соответствующими (по всем параметрам, за исключением R) зависимостями для ранее используемых цепочек шаров радиусом R = 15мм. Тем самым, подтверждая справедливость высказанного выше предположения, можно говорить о том, что с точностью до безразмерных параметров r/R и n полученные результаты, касающиеся, прежде всего, данных индукции магнитного поля в разных (по толщине) сердцевинах цепочек шаров (т.е. кривых намагничивания сердцевин), а также этих данных в зависимости от числа шаров в цепочке, можно распространить на цепочки шаров любого радиуса.

 

Таблица 2 – Магнитный поток Ф, пронизывающий контуры относительного радиуса r/R при числе n шаров в цепочке и напряженности поля H. Диаметр шаров D = 40 мм

Рис. 7 – Полевые зависимости магнитного потока сквозь контуры-петли различного радиуса r, располагаемые в плоскости симметрии объема между шарами радиусом R=20мм, для различного числа шаров n в цепочке; а) n=2, б) n=4, в) n=6, г) n=8, д) n=10, е) n=12, ж) n=14; 1– r/R=0,2, 2– r/R=0,3, 3– r/R=0,4, 4– r/R=0,5, 5– r/R=0,6, 6– r/R=0,7, 7– r/R=0,8, 8– r/R=0,9

Рис. 8 – Полученные по данным рис.4 полевые зависимости индукции (кривые намагничивания) для сердцевин радиусом r, условно выделяемых в цепочке шаров (R=20мм); обозначения соответствуют обозначениям на рис.7

Рис. 9 – Зависимости индукции в сердцевине (радиусом r) цепочки шаров радиусом R =20мм от числа шаров, при различной напряженности поля H; а) H=4,8кА/м, б) H=14,8кА/м, в) H=29,7кА/м, г) H=54,5кА/м; 1– r/R=0,2, 2– r/R=0,3, 3– r/R=0,4, 4– r/R=0,5, 5– r/R=0,6, 6– r/R=0,7, 7– r/R=0,8, 8– r/R=0,9

  Заключение

Аргументирована актуальность экспериментальной диагностики магнитных параметров в таких специфичных микрообъемах как клинообразные зоны между контактирующими гранулами-шарами в намагничиваемой цепочке шаров, являющейся ключевым компонентом структур гранулированных сред, например, используемых в качестве фильтр-матриц магнитных сепараторов фильтрационного типа.

Описаны особенности этой диагностики, даны и реализованы рекомендации использования для этой цели (вместо трудоемких в изготовлении и неоперативных в позиционировании датчиков в виде системы концентричных петель из провода малого диаметра) датчиков в виде весьма тонких контуров (до 10мкм), специально выполненных на печатных платах, помещаемых в плоскости симметрии микрообъема между смежными шарами в средней части цепочки.  Отмечена необходимость расширения круга задач экспериментальных исследований, в частности, за счет увеличения числа разных по радиусу датчиков такого рода, использования образцов-цепочек разной длины (разного числа в ней шаров) и разного диаметра (переходя от цепочек шаров определенного диаметра к цепочкам шаров иного диаметра).

Изложены результаты экспериментальных исследований цепочек шаров радиусом R = 15мм и дополнительно цепочек шаров радиусом R = 20мм в магнитном поле длинного соленоида – при различных значениях напряженности намагничивающего поля H = 4,8-54,5кА/м и числа шаров в цепочке n = 2-14. В исследованиях с помощью упомянутых датчиков, подключаемых к микровеберметру, измерялся магнитный поток Ф сквозь их контуры-петли различного относительного радиуса r/R = 0,2-0,9.

Получены семейства (по r/R и n) полевых зависимостей Ф, а на их основе – соответствующие семейства полевых зависимостей магнитной индукции B (в каждой по значению r/R условной сердцевине цепочки шаров). Установлен регрессирующий (но без признаков приближающего насыщения) рост полевых зависимостей B.

Показано, что при увеличении r/R, т.е. по мере «утолщения» условных сердцевин, несмотря на увеличение значений Ф, значения B снижаются – ввиду уменьшения объема металла в сердцевине цепочки.

Выявлено, что цепочки, характеризующиеся относительно малыми значениями n, по всем сердцевинным значения Ф и B уступают более длинным цепочкам: из-за большего проявления размагничивающего фактора «коротких» цепочек шаров; значения Ф и B стабилизируются (достигая области автомодельности) при n = 10-12 (независимо от радиуса шаров).

На примере взаимного согласия кривых B от r/R и n для цепочек одинаковых шаров, но при использовании в них шаров сначала одного, а затем другого радиуса, показана возможность универсализации получаемых данных B (для других цепочек одинаковых шаров).

Финансирование Исследование выполнено при финансовой поддержке Минобрнауки РФ в рамках Госзадания в сфере науки - проект № 0706-2020-0024; гранта Президента РФ для господдержки молодых ученых – проект МК-807.2020.8.	Funding The research is conducted with financial support from Russian Federation Ministry of Education and Science within the frameworks of state assignment – project №0706-2020-0024; President’ grant – project МК-807.2020.8.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Сандуляк А. В. Магнитно-фильтрационная очистка жидкостей и газов. / А. В. Сандуляк – М.: Химия, 1988. – 136 с. – URL: https://dlib.rsl.ru/viewer/01001440011#?page=136
2. Сандуляк А. В. Магнитные характеристики «короткого» пористого магнетика: на примере засыпки шаров / А. В. Сандуляк, Д. А. Сандуляк, В. А. Ершова, Р. Ю. Ткаченко, А. А. Сандуляк, М. Н. Полисмакова // Фундаментальные и прикладные проблемы техники и технологии. – 2019. – № 3 (335). – С. 121–133.
3. Eskandarpour A. Superconducting magnetic filter: Performance, recovery, and design / A. Eskandarpour, K. Iwai, S. Asai // IEEE Transactions on Applied Superconductivity. – 2008. – V. 19 (2) – art. no.4799183. – P. 84–95.
4. Anhalt M. Systematic investigation of particle size dependence of magnetic properties in soft magnetic composites / M. Anhalt // Journal of Magnetism and Magnetic Materials. – 2008. – V. 320. – P. e366–e369.
5. Mattei J. L. Study of magnetic percolation in heterogeneous materials / J. L. Mattei, O. Minot, M. Le Floc’h // Journal of Magnetism and Magnetic Materials. – 1995. – V. 140–144 (3). – P. 2189–2190.
6. Bjork R. The demagnetization factor for randomly packed spheroidal particles / R. Bjork, Z. Zhou // Journal of Magnetism and Magnetic Materials. – 2019. – V. 476. – P. 417–422.
7. Mishima F. Research and development of superconducting magnetic separation system for powdered products / F. Mishima, T. Terada, Y. Akiyama, Y. Izumi, H. Okazaki, S. Nishijima // IEEE Transactions on Applied Superconductivity. – 2008. – V. 18 (2) – art. no.4520245. – P. 824–827.
8. Diguet G. Shape effect in the magnetostriction of ferromagnetic composite / G. Diguet, E. Beaugnon, J. Y. Cavaillé // Journal of Magnetism and Magnetic Materials. – 2010. – V. 322. – P. 3337–3341.
9. Сандуляк А. В. К вопросу о модели поканального намагничивания гранулированной среды (с радиальным профилем проницаемости квазисплошного канала) / А. В. Сандуляк, А. А. Сандуляк, В. А. Ершова // Журнал технической физики. – 2009. – Т. 79. – вып.5. – С. 140–142.
10. Sandulyak A. V. Magnetization curve of a granulated medium in terms of the channel-by-channel magnetization model (new approach) / A. V. Sandulyak, A. A. Sandulyak, V. A. Ershova // Doklady Physics. – 2007. – V. 52. – № 4. – Р. 179–181.
11. Sandulyak A. A. Ferrous Material Fill: Magnetization Channels, Layer-by-Layer and Average Permeability, Element-to-Element Field / A. A. Sandulyak, D. A. Sandulyak, V. A. Ershova, A. V. Sandulyak // Analysis and Modelling of Advanced Structures and Smart Systems. – 2017. – V. 81. – P.191–210.
12. Кифер И. И. Испытания ферромагнитных материалов. / И. И. Кифер // М.: Энергия, 1969. – 360 с.
13. Chen D. X. Demagnetizing correction in fluxmetric measurements of magnetization curves and hysteresis loops of ferromagnetic cylinders / D. X. Chen, E. Pardo, Y.-H. Zhu, L.-X. Xiang, J.-Q. Ding // Journal of Magnetism and Magnetic Materials. – 2018. – V. 449. – P. 447–454.
14. Périgo E. A. Past, present, and future of soft magnetic composites / E. A. Périgo, B. Weidenfeller, P. Kollár, J. Füzer // Applied Physics Reviews. – 2018. – V. 5. – P. 031301.

Список литературы на английском языке / References in English

1. Sandulyak A. V. Magnitno-fil'tracionnaja ochistka zhidkostej i gazov [Magnetic and filtration purification of liquids and gases] / Moscow. Chem. 136 (1988) pp. – URL: https://dlib.rsl.ru/viewer/01001440011#?page=136 [in Russian]
2. Sandulyak A. V. Magnitnye harakteristiki «korotkogo» poristogo magnetika: na primere zasypki sharov [Magnetic characteristics of «short» porous magnetic: by the example of filling of spheres] / A. V. Sandulyak, D. A. Sandulyak, V. A. Ershova, R. Y. Tkachenko, A. A. Sandulyak, M. N. Polismakova // Fundamental and Applied Problems of Technics and Technology. – 2019. – № 3 (335). – P. 121–133. [in Russian]
3. Eskandarpour A. Superconducting magnetic filter: Performance, recovery, and design / A. Eskandarpour, K. Iwai, S. Asai // IEEE Transactions on Applied Superconductivity. – 2008. – V. 19 (2) – art. no.4799183. – P. 84–95.
4. Anhalt M. Systematic investigation of particle size dependence of magnetic properties in soft magnetic composites / M. Anhalt // Journal of Magnetism and Magnetic Materials. – 2008. – V. 320. – P. e366–e369.
5. Mattei J. L. Study of magnetic percolation in heterogeneous materials / J. L. Mattei, O. Minot, M. Le Floc’h // Journal of Magnetism and Magnetic Materials. – 1995. – V. 140–144 (3). – P. 2189–2190.
6. Bjork R. The demagnetization factor for randomly packed spheroidal particles / R. Bjork, Z. Zhou // Journal of Magnetism and Magnetic Materials. – 2019. – V. 476. – P. 417–422.
7. Mishima F. Research and development of superconducting magnetic separation system for powdered products / F. Mishima, T. Terada, Y. Akiyama, Y. Izumi, H. Okazaki, S. Nishijima // IEEE Transactions on Applied Superconductivity. – 2008. – V. 18 (2) – art. no.4520245. – P. 824–827.
8. Diguet G. Shape effect in the magnetostriction of ferromagnetic composite / G. Diguet, E. Beaugnon, J. Y. Cavaillé // Journal of Magnetism and Magnetic Materials. – 2010. – V. 322. – P. 3337–3341.
9. Sandulyak A. V. K voprosu o modeli pokanal'nogo namagnichivanija granulirovannoj sredy (s radial'nym profilem pronicaemosti kvazisploshnogo kanala) [On the model of channel-by-channel magnetization of a granular medium (with a radial permeability profile of a quasi-continuous channel)] / A. V. Sandulyak, A. A. Sandulyak, V. A. Ershova // Technical Physics. – 2009. – V. 54. – N5. – P. 743–745. [in Russian]
10. Sandulyak A. V. Magnetization curve of a granulated medium in terms of the channel-by-channel magnetization model (new approach) / A. V. Sandulyak, A. A. Sandulyak, V. A. Ershova // Doklady Physics. – 2007. – V. 52. – № 4. – Р. 179–181.
11. Sandulyak A. A. Ferrous Material Fill: Magnetization Channels, Layer-by-Layer and Average Permeability, Element-to-Element Field / A. A. Sandulyak, D. A. Sandulyak, V. A. Ershova, A. V. Sandulyak // Analysis and Modelling of Advanced Structures and Smart Systems. – 2017. – V. 81. – P.191–210.
12. Kifer I. I. Ispytanija ferromagnitnyh materialov [Ispitanya ferromagnitnyh materialov]. / I. I. Kifer // Moscow: Energy Publ., 1969. – 360 p. [in Russian]
13. Chen D. X. Demagnetizing correction in fluxmetric measurements of magnetization curves and hysteresis loops of ferromagnetic cylinders / D. X. Chen, E. Pardo, Y.-H. Zhu, L.-X. Xiang, J.-Q. Ding // Journal of Magnetism and Magnetic Materials. – 2018. – V. 449. – P. 447–454.
14. Périgo E. A. Past, present, and future of soft magnetic composites / E. A. Périgo, B. Weidenfeller, P. Kollár, J. Füzer // Applied Physics Reviews. – 2018. – V. 5. – P. 031301.