МОНИТОРИНГ КАЧЕСТВА ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА НА ОСНОВЕ АНАЛИЗА ПСИХОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
МОНИТОРИНГ КАЧЕСТВА ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА НА ОСНОВЕ АНАЛИЗА ПСИХОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
Научная статья
Полещук О.М.1, Комаров Е.Г.2, Малолепшая Н.Э.
1Д.т.н., проф.
2Д.т.н., проф.
г. Мытищи, Московский государственный университет леса, ул. 1-ая Институтская д. 1
Аннотация
Основная проблема при мониторинге качества образовательного процесса состоит в том, что оно определяется разнородными характеристиками, для которых не всегда корректны арифметические операции и, следовательно традиционные рейтинговые методы. В статье предлагается подход, который позволяет оперировать не со значениями самих характеристик, а со значениями их функций принадлежности.
Ключевые слова: образовательный процесс, лингвистическая шкала, рейтинговая оценка.
Key words: educational process, linguistic scale, rating point.
Среди измеряемых и контролируемых характеристик, определяющих качество образовательных услуг, существенное положение занимают показатели качества подготовки студентов и выпускников на основе их успеваемости. Для анализа результатов подготовки студентов используются показатели их успеваемости по циклам дисциплин: фундаментальным, общепрофессиональным и специальным. Однако показатели успеваемости не всегда дают действительную картину состояния процесса обучения. Это связано со сложностью оценивания проявления знаний, которая состоит в учете субъективных взглядов, мнений и опыта лиц, производящих оценивание и принимающих на основе этого субъективного оценивания решения.
С целью увеличения достоверности выводов о состоянии образовательного процесса, полученных в результате анализа показателей успеваемости, предлагается наряду с анализом этих показателей проводить анализ познавательных психофизиологических характеристик студентов в рамках, например, ежегодного их мониторинга. Эти характеристики могут определяться на основе тестов экспресс – диагностики интеллектуального развития, которые относятся к категории тестов общих умственных способностей. В этих тестах обследуемому предъявляется серия заданий, подобранных таким образом, чтобы была обеспечена адекватная оценка интеллектуальных функций. Подобные тесты дают возможность определения таких важнейших компонент интеллекта, как: грамотность, точность восприятия, логичность мышления, пространственное воображение, скорость мыслительных процессов.
Оценивание всех компонент проводится, не ограничивая общности, в рамках вербальной шкалы: «очень низкий уровень», «низкий уровень», «средний уровень», «высокий уровень», «очень высокий уровень». Используя для оценивания качественных признаков слова естественного языка, человек закладывает в свои оценки неопределенность в виде нечеткости. В разговорном языке часто понятия неопределенности, нечеткости и случайности смешиваются в одно понятие. На языке науки давно произошло разграничение этих понятий. Неопределенность разделяется на физическую неопределенность и лингвистическую неопределенность. Физическая неопределенность в свою очередь разделяется на неточность, которой занимается теория измерений, и случайность, которой занимается теория вероятностей. Лингвистическая неопределенность разделяется на неопределенность смысла фраз, которой занимается теория формальных грамматик, и неопределенность смысла слов, которой занимается теория нечетких множеств. Основной задачей оценивания качественных признаков является задача нахождения количественных значений этих признаков. Применяя аппарат теории нечетких множеств, появилась возможность определения степени интенсивности проявления исследуемого качественного признака. Таким образом, анализ изменения познавательных психофизиологических характеристик предлагается проводить на основе аппарата теории нечетких множеств [1, 2].
В основании любой теории областей естествознания лежит понятие элементарного объекта, которое является очень важным и основополагающим для построения этих теорий. Для теории нечетких множеств таким понятием является понятие нечеткого множества, которое по Л.А. Заде определяется своей функцией принадлежности. Фиксирование конкретных значений функции принадлежности носит субъективный характер. Дадим определение нечеткого множества согласно [3].
Пусть Х  - некоторое множество элементов x
- некоторое множество элементов x , и
, и 
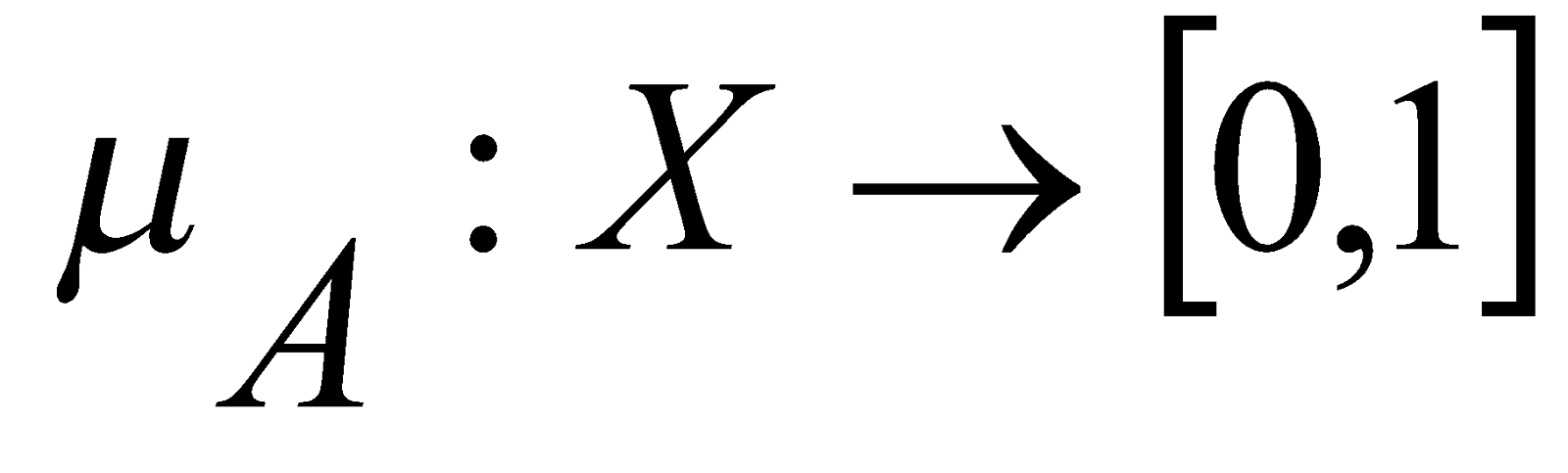 . Нечетким подмножеством
. Нечетким подмножеством 
 в
в  X называется график отображения
X называется график отображения 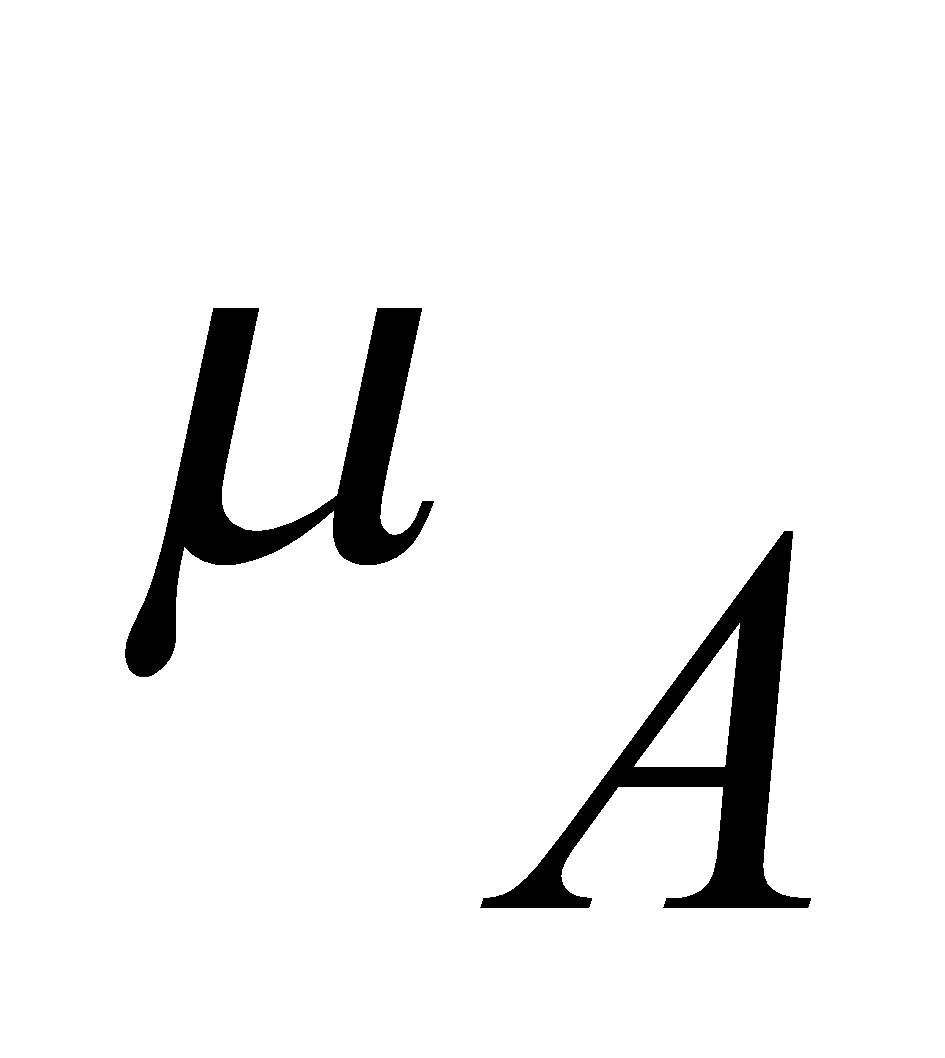
 , то есть множество вида
, то есть множество вида 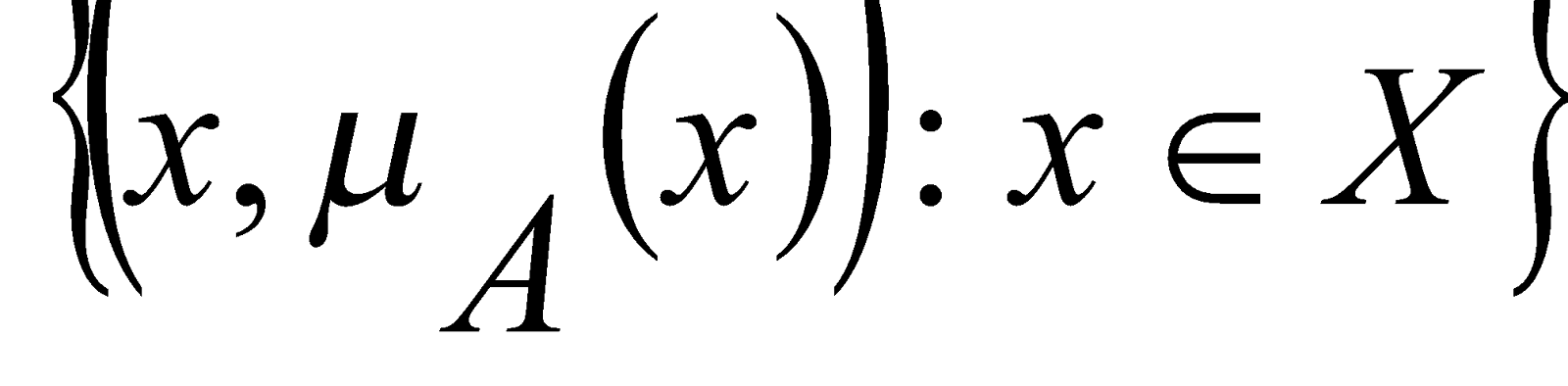
 ; при этом значение
; при этом значение 
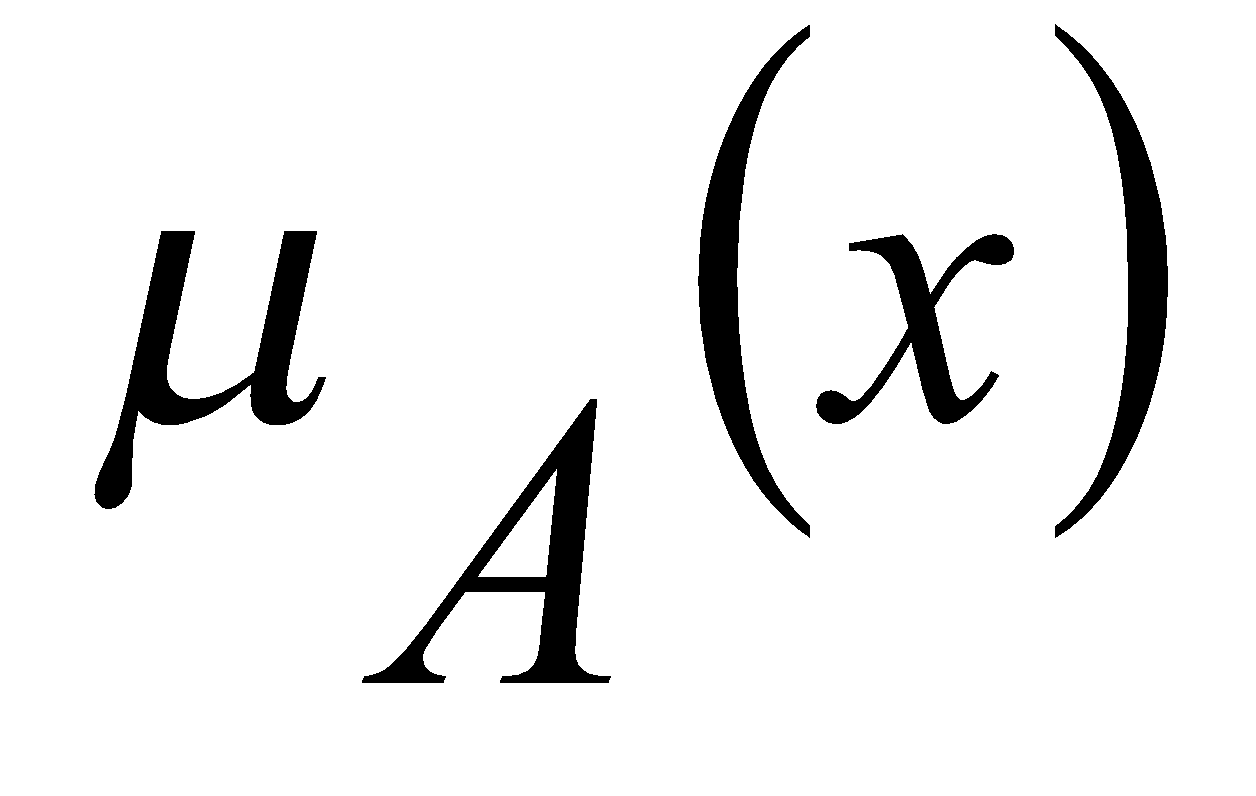 называется степенью принадлежности
называется степенью принадлежности  x к
x к 
 .
.
Из определения следует, что задание нечеткого подмножества 
 в X
в X  эквивалентно заданию его функции принадлежности
эквивалентно заданию его функции принадлежности 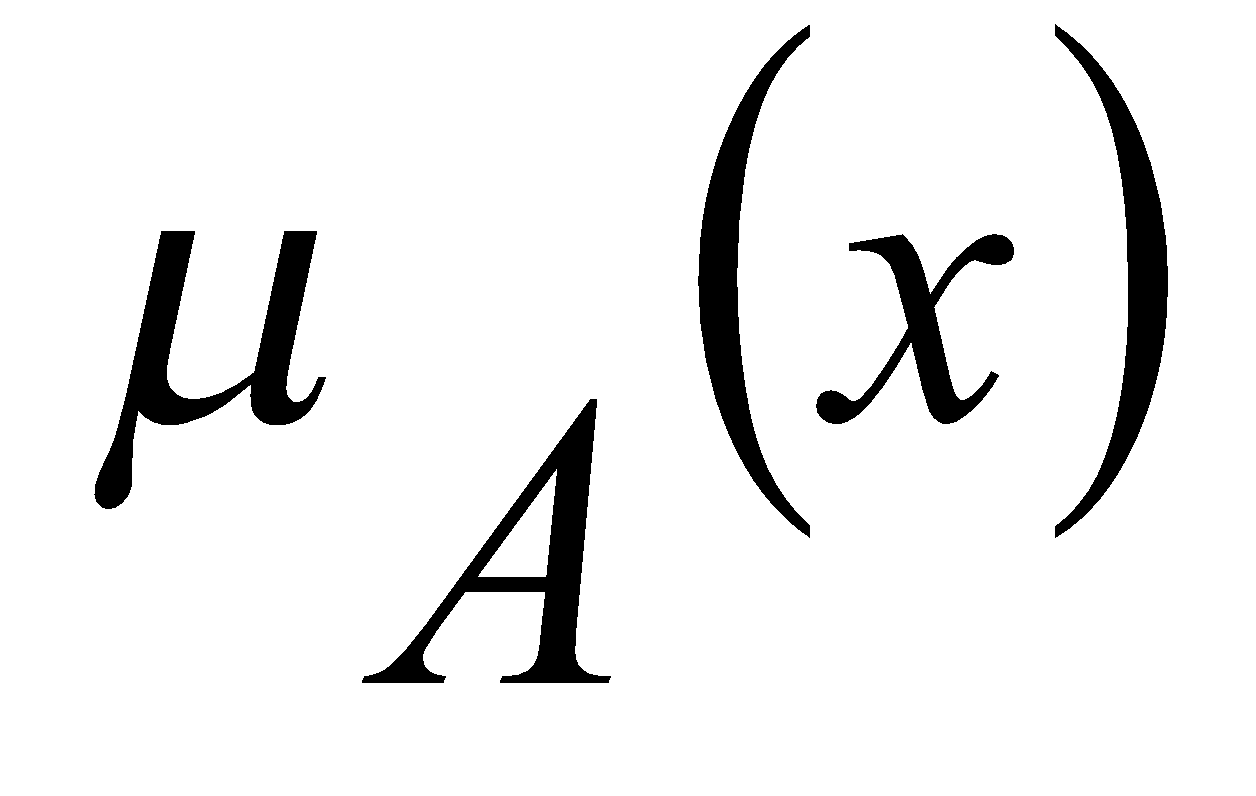
 . Следуя сложившейся традиции, будем употреблять термин «нечеткое множество» вместо более корректного термина «нечеткое подмножество».
. Следуя сложившейся традиции, будем употреблять термин «нечеткое множество» вместо более корректного термина «нечеткое подмножество».
Значение функции принадлежности 
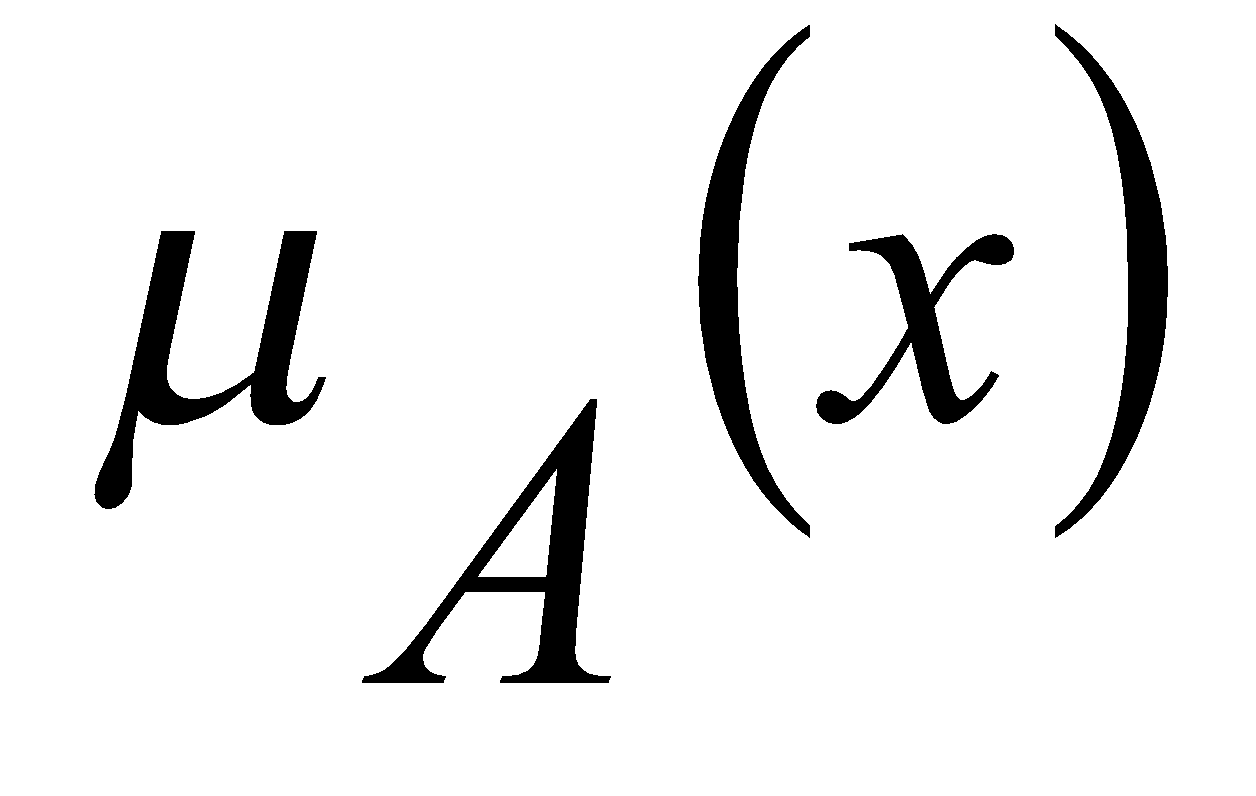 элемента
элемента  x к нечеткому множеству
x к нечеткому множеству 
 можно интерпретировать как определенная экспертом (группой экспертов) степень соответствия элемента
можно интерпретировать как определенная экспертом (группой экспертов) степень соответствия элемента  понятию, формализуемому нечетким множеством
понятию, формализуемому нечетким множеством 
 .
.
Одним из основных понятий теории нечетких множеств является понятие нечеткой переменной [4].
Нечеткой переменной называется тройка
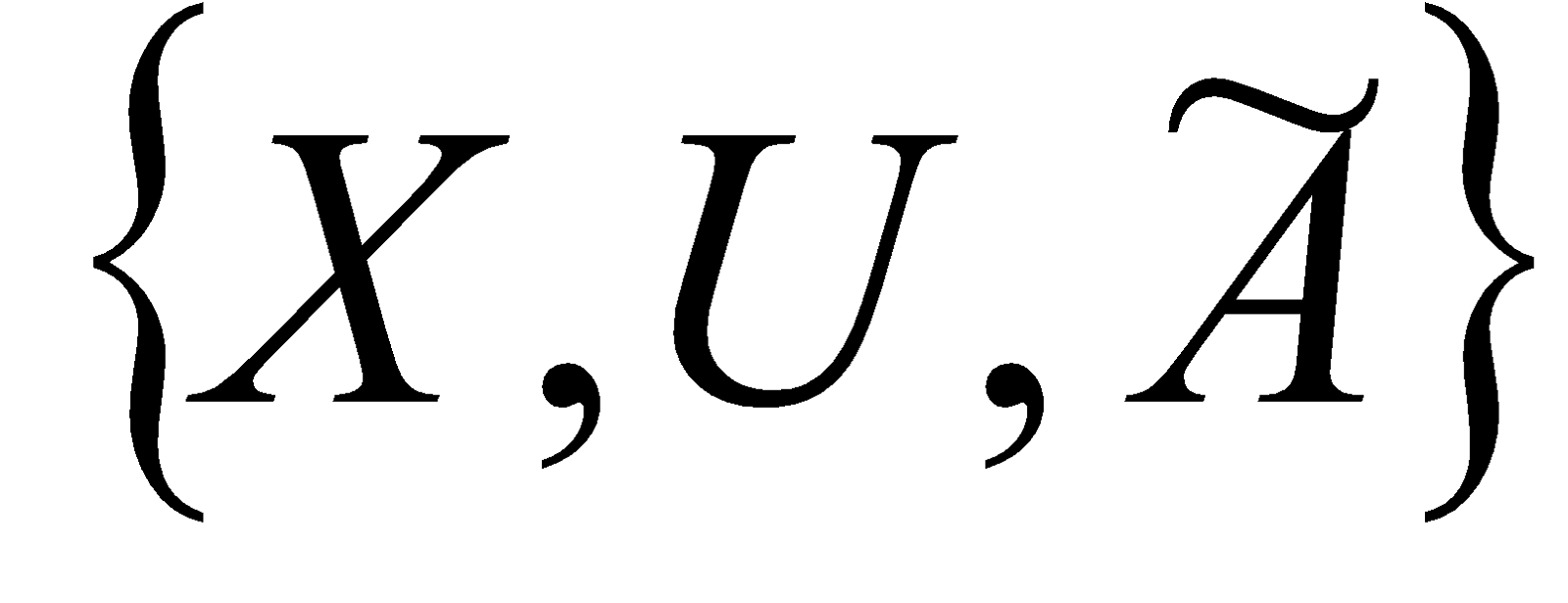
 ,
,
где X  - название переменной; U
- название переменной; U - область ее определения (универсальное множество);
- область ее определения (универсальное множество); 
 - нечеткое множество универсального множества, описывающее возможные значения нечеткой переменной.
- нечеткое множество универсального множества, описывающее возможные значения нечеткой переменной.
На основе понятия нечеткой переменной вводится понятие лингвистической переменной [4].
Лингвистической переменной называется пятерка
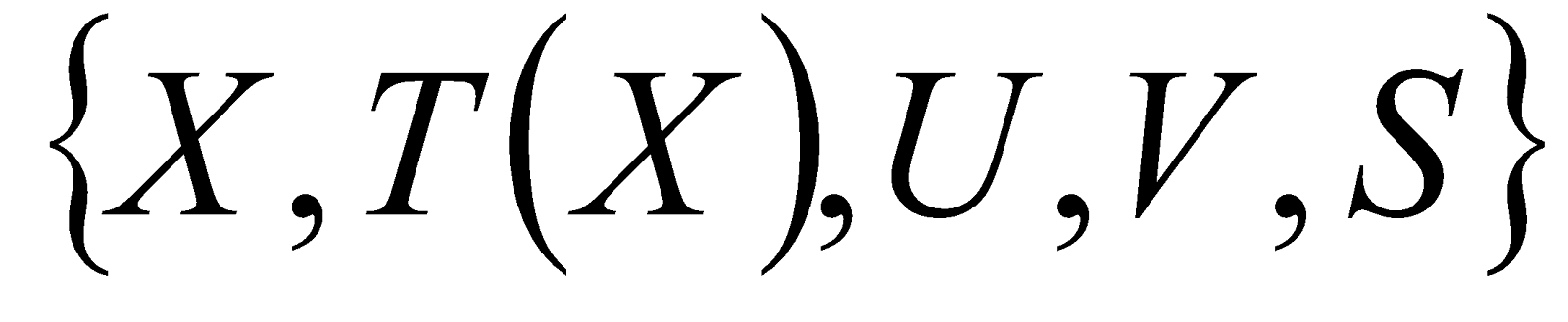
 ,
,
где X  - название переменной;
- название переменной; 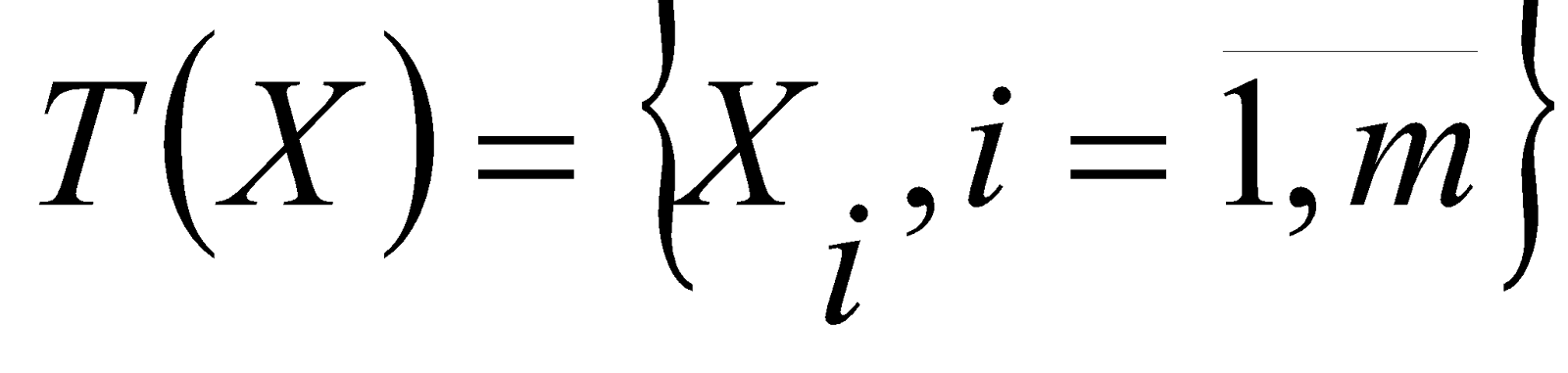
 - терм-множества переменной X
- терм-множества переменной X  , то есть множество названий лингвистических значений переменной X
, то есть множество названий лингвистических значений переменной X  . Каждое из этих значений – нечеткая переменная со значениями из универсального множества U
. Каждое из этих значений – нечеткая переменная со значениями из универсального множества U  . V
. V  - синтаксическое правило, порождающее названия значений лингвистической переменной X
- синтаксическое правило, порождающее названия значений лингвистической переменной X  . S
. S - семантическое правило, которое ставит в соответствие каждой нечеткой переменной с названием T(X) из
- семантическое правило, которое ставит в соответствие каждой нечеткой переменной с названием T(X) из  нечеткое подмножество универсального множества U
нечеткое подмножество универсального множества U  .
.
Терм-множества 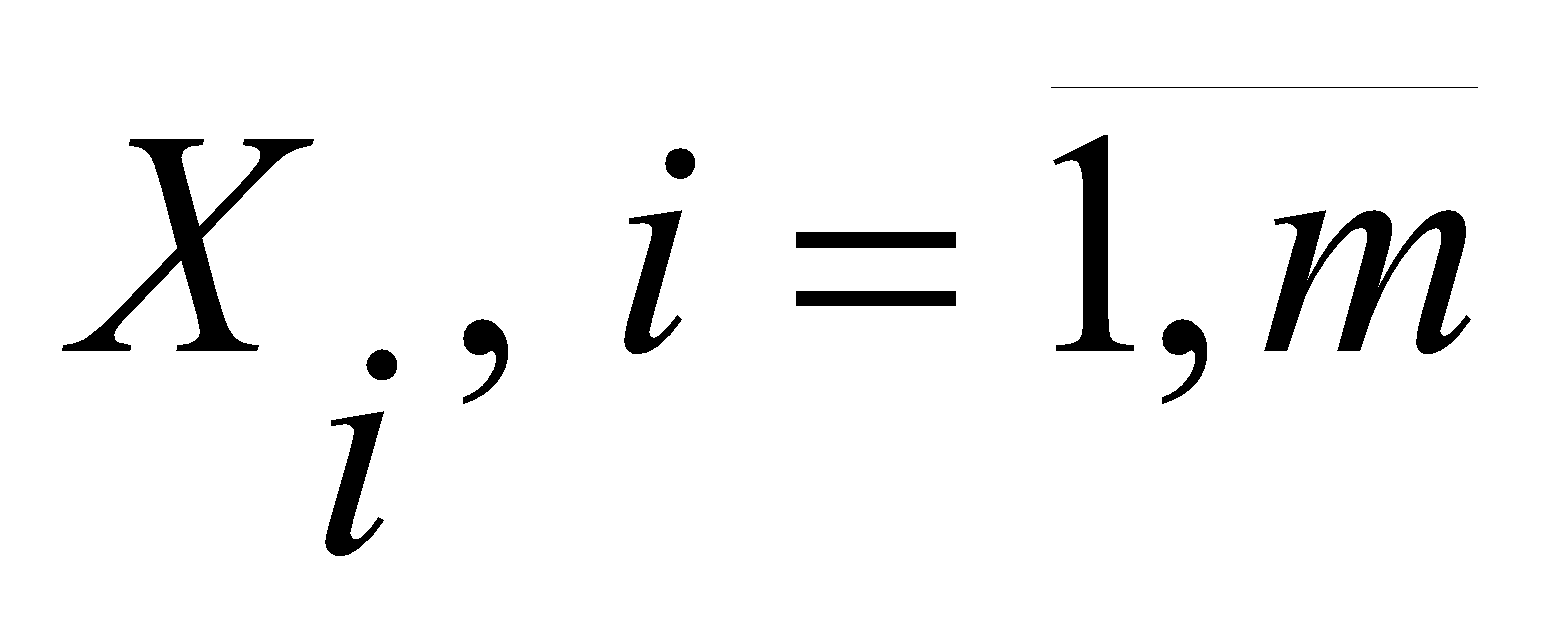
 называют понятиями, которые образуют лингвистическую переменную [5]. Функцию принадлежности нечеткого множества, описывающего возможные значения нечеткой переменной с названием
называют понятиями, которые образуют лингвистическую переменную [5]. Функцию принадлежности нечеткого множества, описывающего возможные значения нечеткой переменной с названием 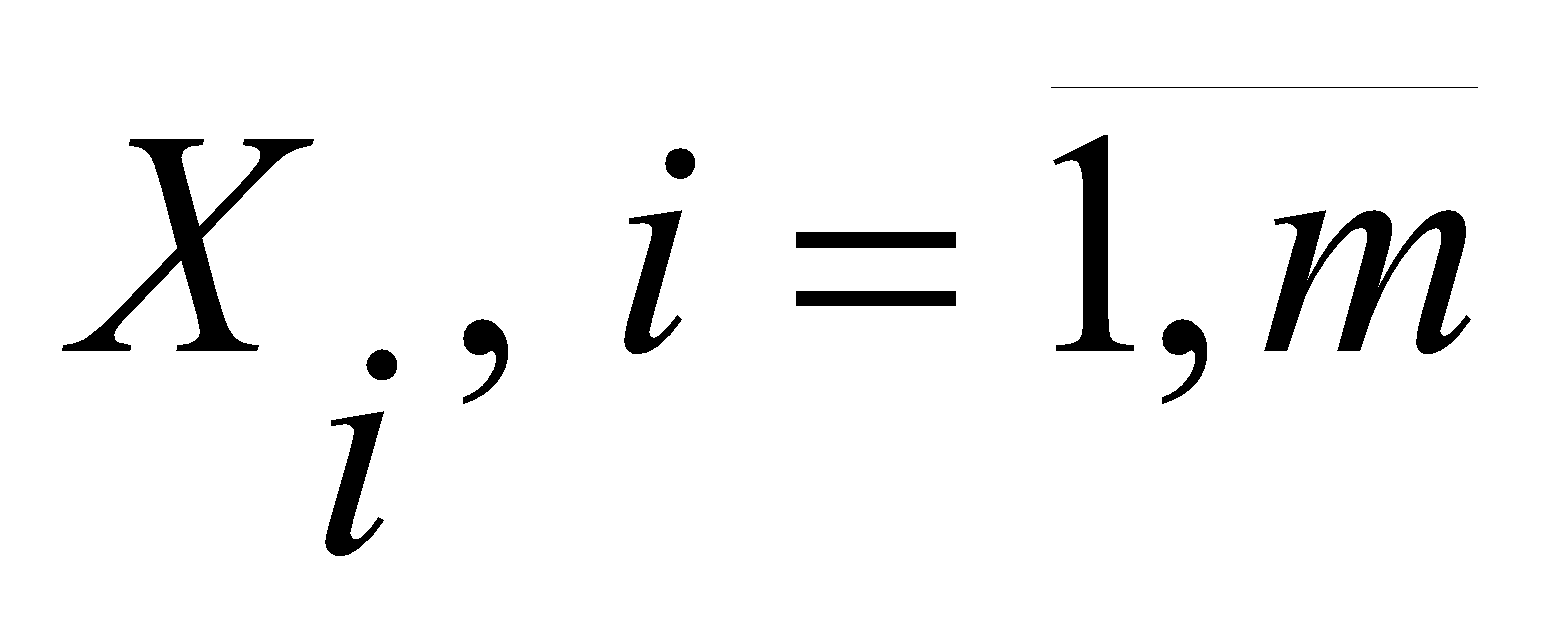
 , традиционно называют функцией принадлежности понятия
, традиционно называют функцией принадлежности понятия 
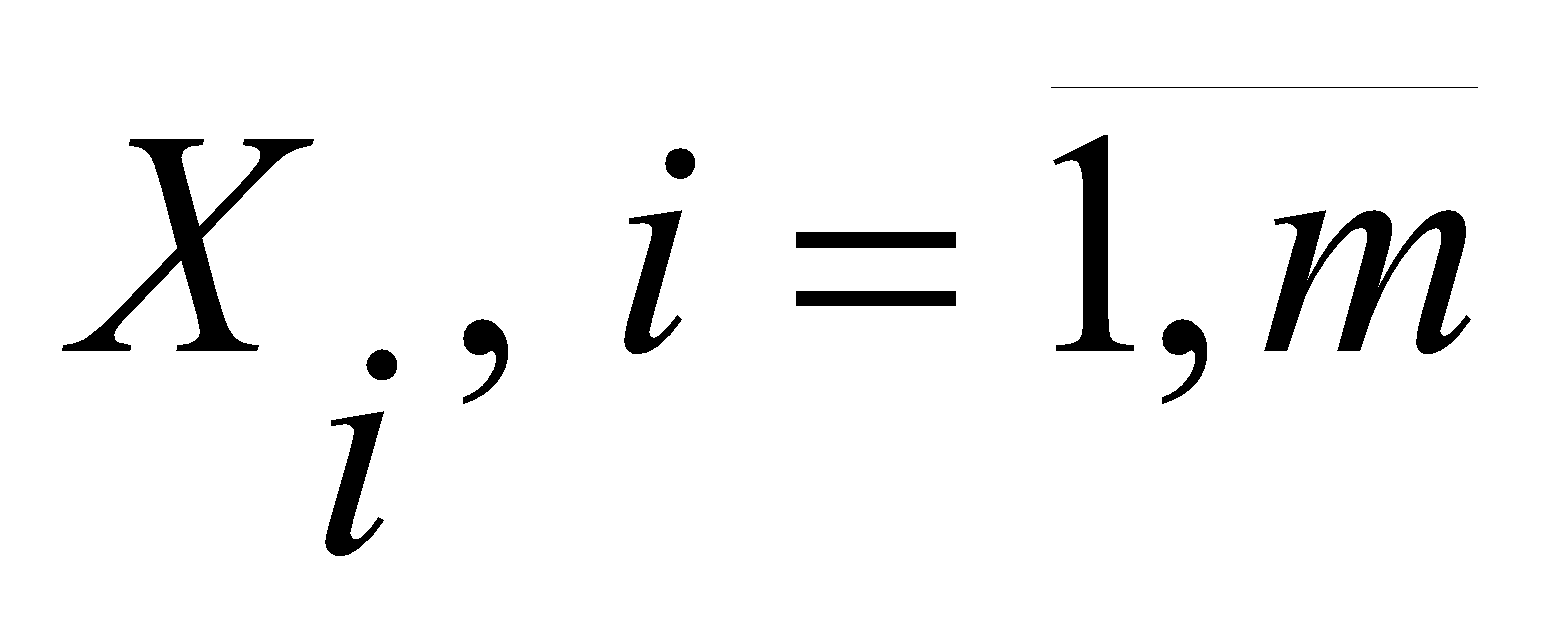 или функцией принадлежности терм-множества
или функцией принадлежности терм-множества 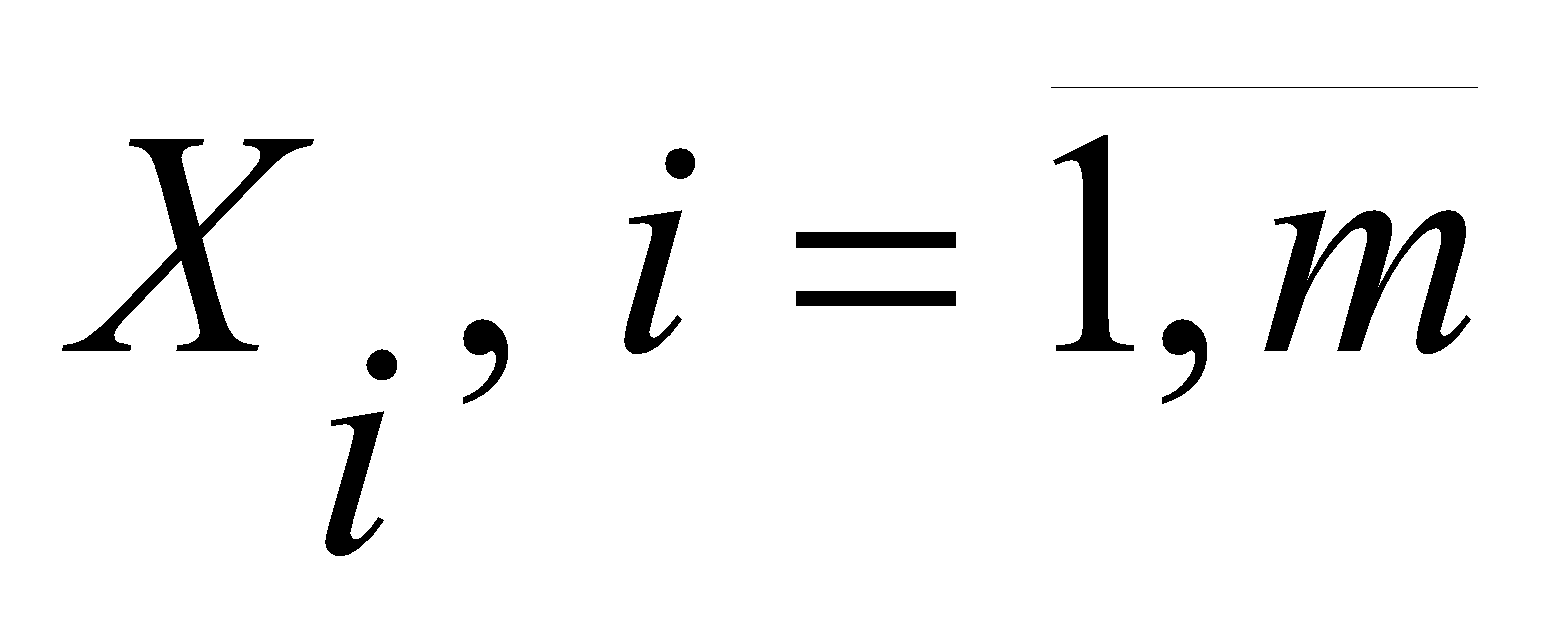
 .
.
Методы построения функций принадлежности терм-множеств находятся вне теории нечетких множеств и поэтому не могут быть проверены в рамках этой теории. Требования к методу построения функций принадлежности формулируются в рамках каждой конкретной задачи [5].
Методы построения функций принадлежности можно разделить на два класса: прямые и косвенные. Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности. Как правило, прямые методы задания функции принадлежности используются для измеримых понятий. Разновидностями прямых методов являются прямые групповые методы, непосредственное задание функции принадлежности таблицей, графиком или формулой.
Косвенные методы построения значений функции принадлежности используются в случаях, когда нет элементарных измеримых свойств, через которые определяются нечеткие множества. В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру ее обработки. К таким методам относятся статистический метод, метод парных сравнений, метод экспертных оценок, метод интервальных оценок и ряд других.
При оценивании экспертом проявлений качественных характеристик естественным является вопрос: «По каким критериям должен производиться выбор множества значений лингвистической шкалы, которая применяется при оценивании той или иной характеристики?». Для оценивания качественных характеристик эксперты могут применять разные множества их лингвистических значений. Одни множества доставляют трудности экспертам в связи с недостаточностью значений, другие в связи с избыточностью значений. В результате этих трудностей следует ожидать, что степень уверенности экспертов в результатах оценивания будет уменьшаться и соответственно увеличиваться нечеткость результатов. Если оценивания производят несколько экспертов, то из-за трудностей оценивания следует ожидать рассогласованности информации, поступающей от разных экспертов.
Исходя из этого, лингвистическую шкалу для оценивания характеристик предлагается строить таким образом, чтобы эксперты испытывали минимальную неопределенность при оценивании, а результаты, полученные от разных экспертов, имели бы максимальную согласованность [6].
Обозначим через 
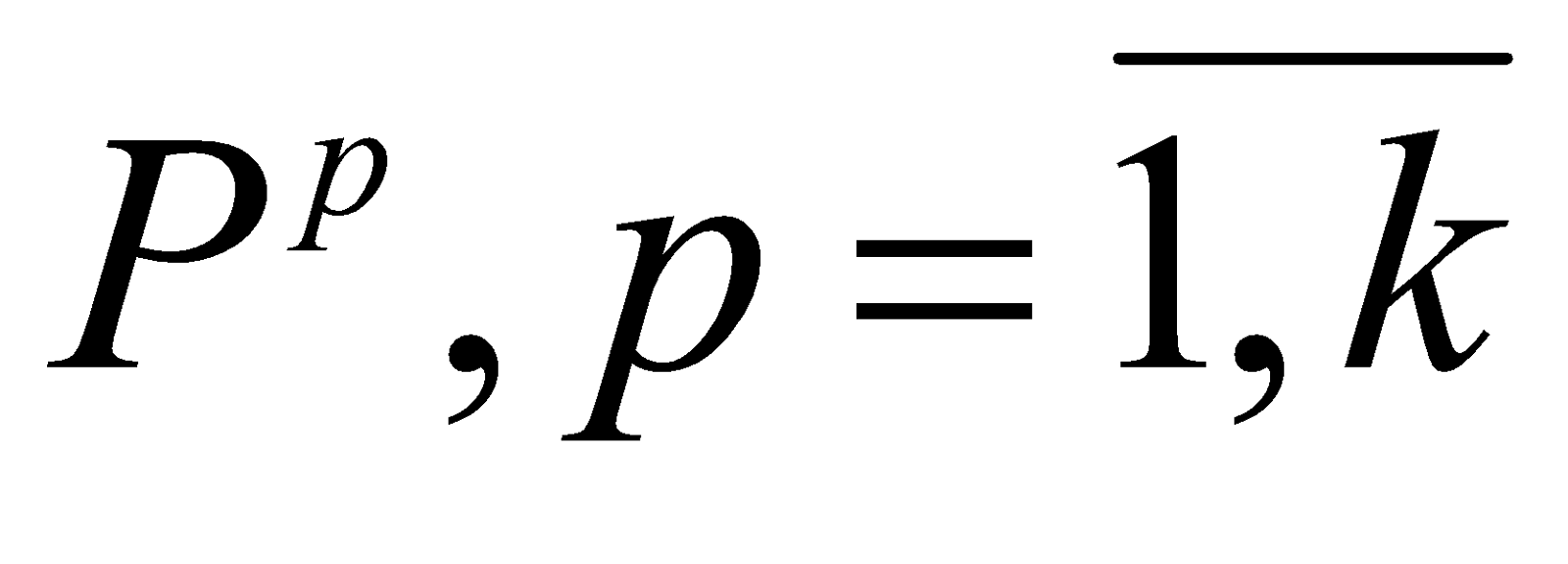 модели оценивания
модели оценивания  k экспертами характеристики X
k экспертами характеристики X , а через
, а через 
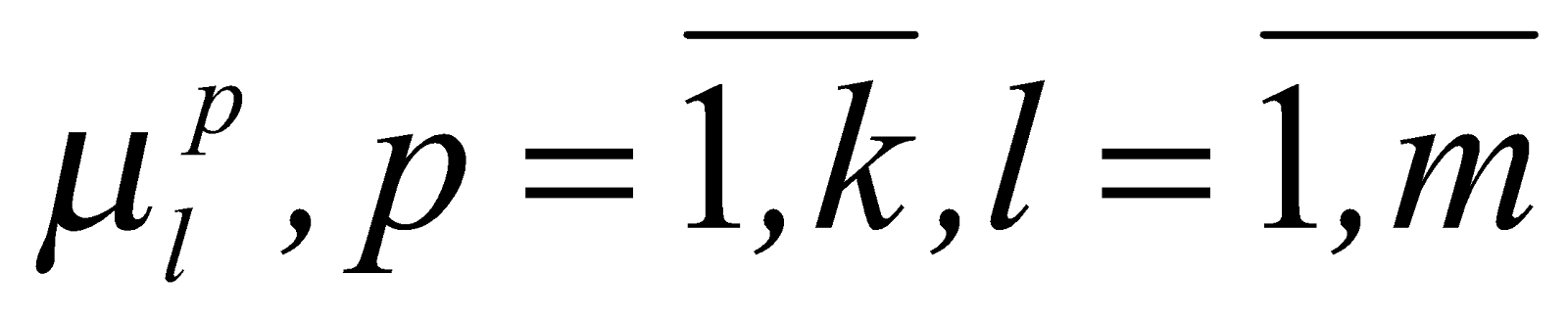 функции принадлежности их термов.
функции принадлежности их термов.
Показателем согласованности экспертной информации назовем
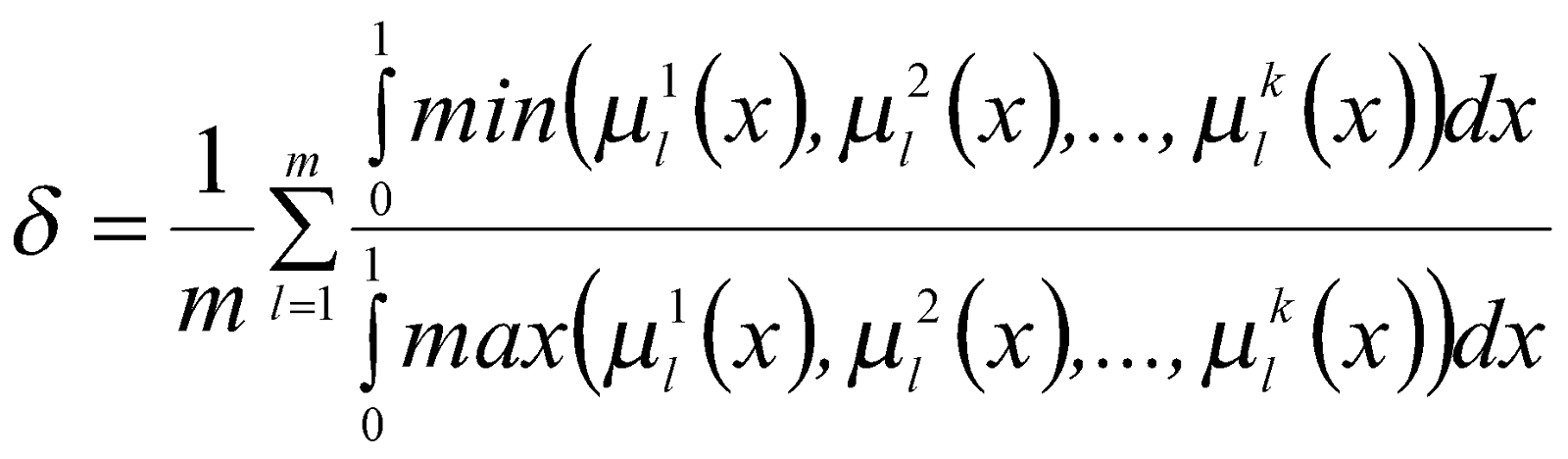
 .
.
Будем предполагать, что для оценивания характеристики  X привлекаются k
X привлекаются k  экспертов, которые формулируют возможные множества лингвистической шкалы
экспертов, которые формулируют возможные множества лингвистической шкалы 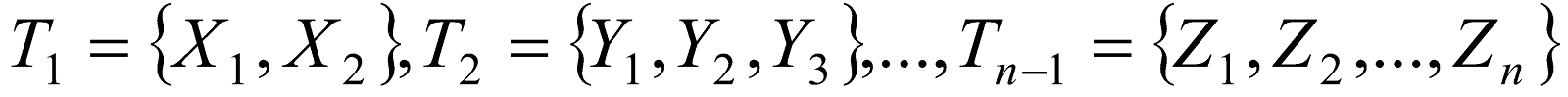
 .Используя информацию, полученную от экспертов и методы [4], построим модели экспертного оценивания характеристики X
.Используя информацию, полученную от экспертов и методы [4], построим модели экспертного оценивания характеристики X , которые обозначим через
, которые обозначим через 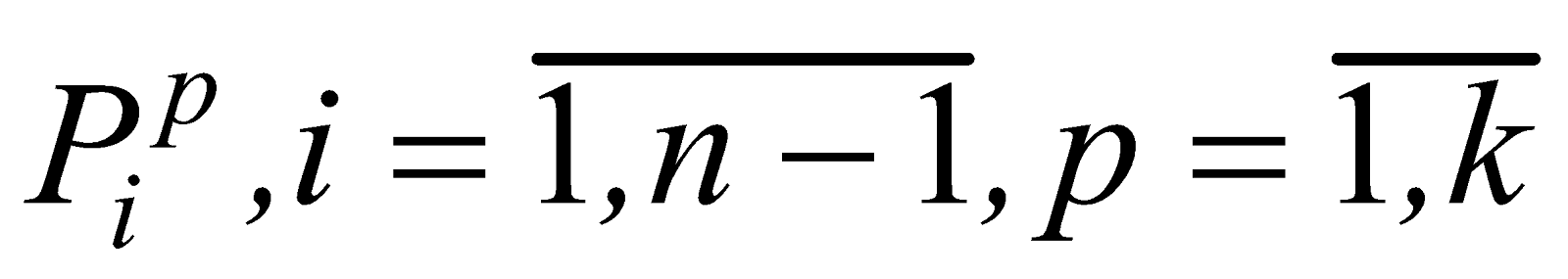 . Методы построения этих моделей могут опираться на непосредственный опрос экспертов или на статистическую информацию, полученную на основе оценочных мероприятий экспертов в прошлом.
. Методы построения этих моделей могут опираться на непосредственный опрос экспертов или на статистическую информацию, полученную на основе оценочных мероприятий экспертов в прошлом.
Рассмотрим модели 
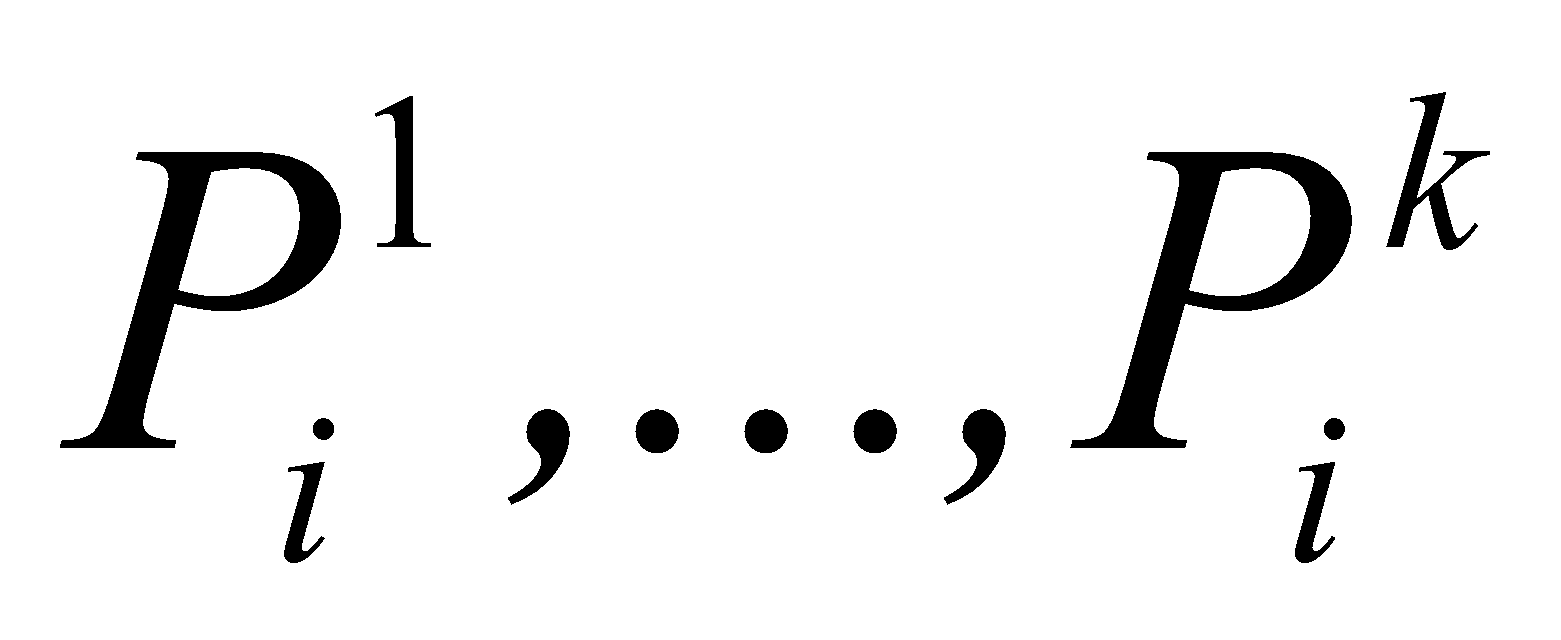 в рамках терм-множества
в рамках терм-множества 
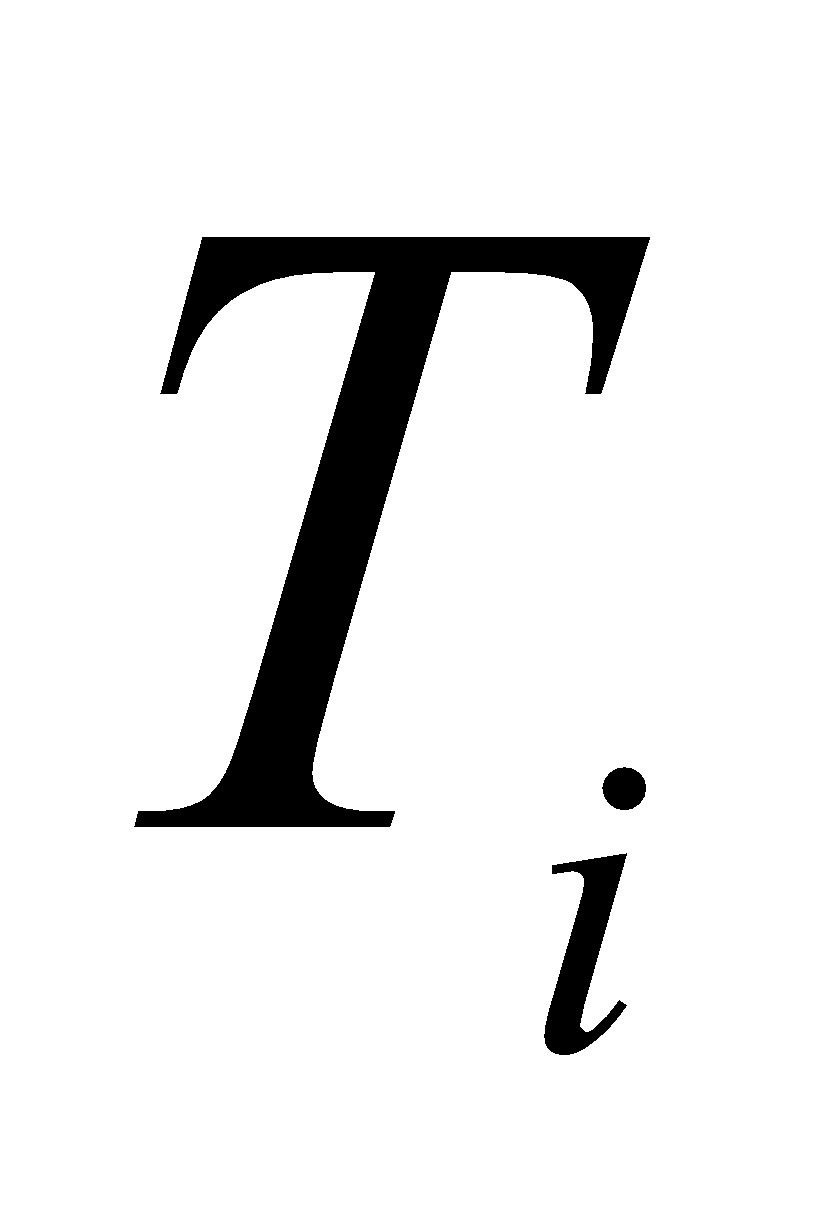 и обозначим их функции принадлежности через
и обозначим их функции принадлежности через 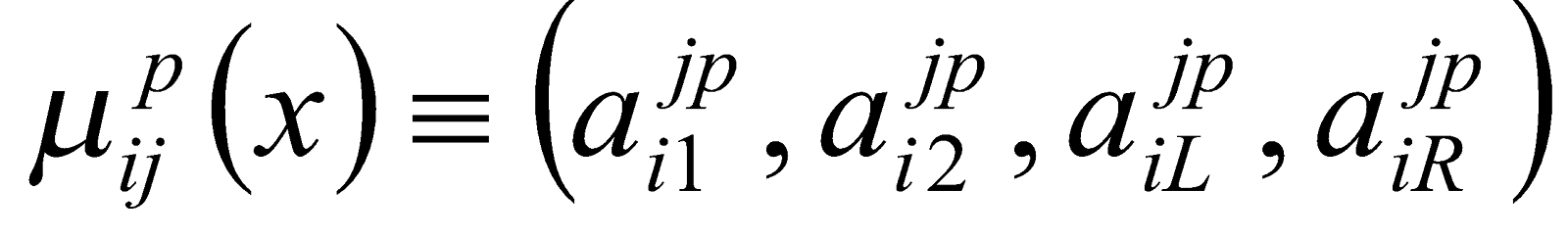
 ,
,
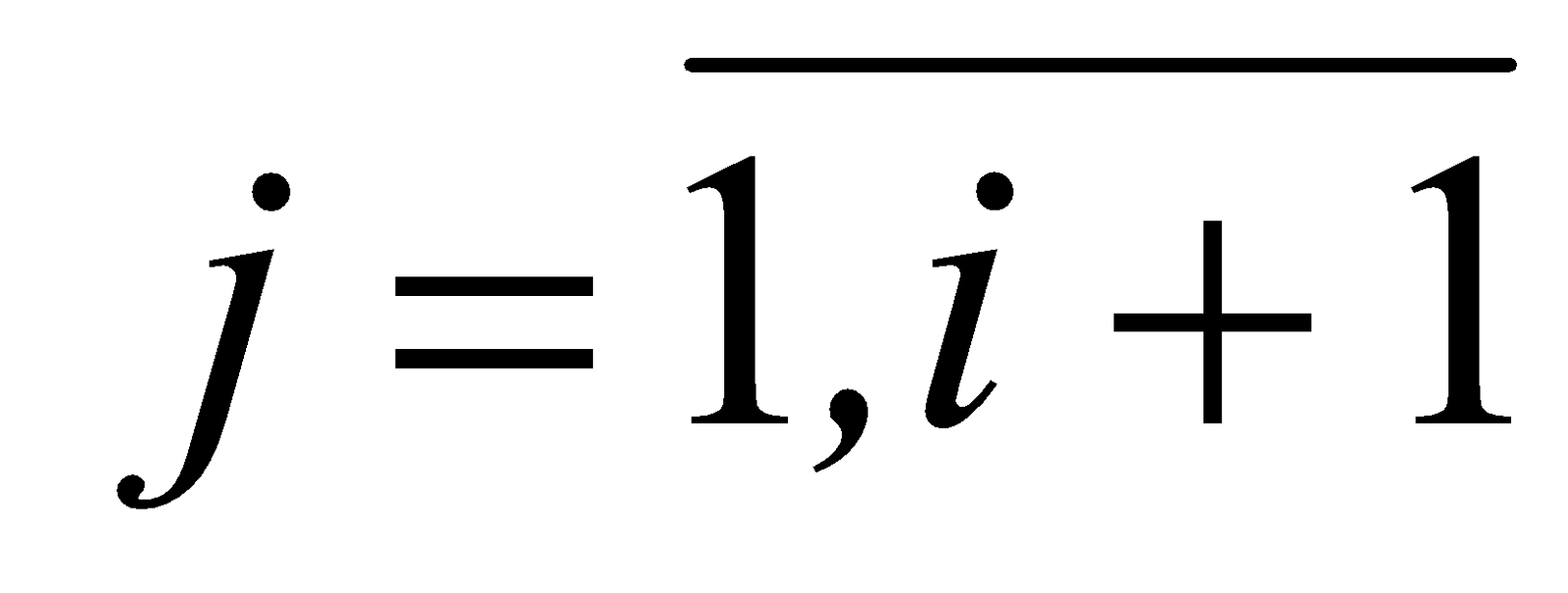 . Первые два параметра в скобках являются абсциссами соответственно левой и правой верхних вершин трапеций – графиков функций принадлежности. Последние два параметра являются длинами соответственно левого и правого крыльев трапеций. В случае треугольных нечетких чисел первые два параметра равны, поэтому треугольное число определяется тремя параметрами.
. Первые два параметра в скобках являются абсциссами соответственно левой и правой верхних вершин трапеций – графиков функций принадлежности. Последние два параметра являются длинами соответственно левого и правого крыльев трапеций. В случае треугольных нечетких чисел первые два параметра равны, поэтому треугольное число определяется тремя параметрами.
Обозначим обобщенную модель экспертного оценивания в рамках шкалы с терм-множеством 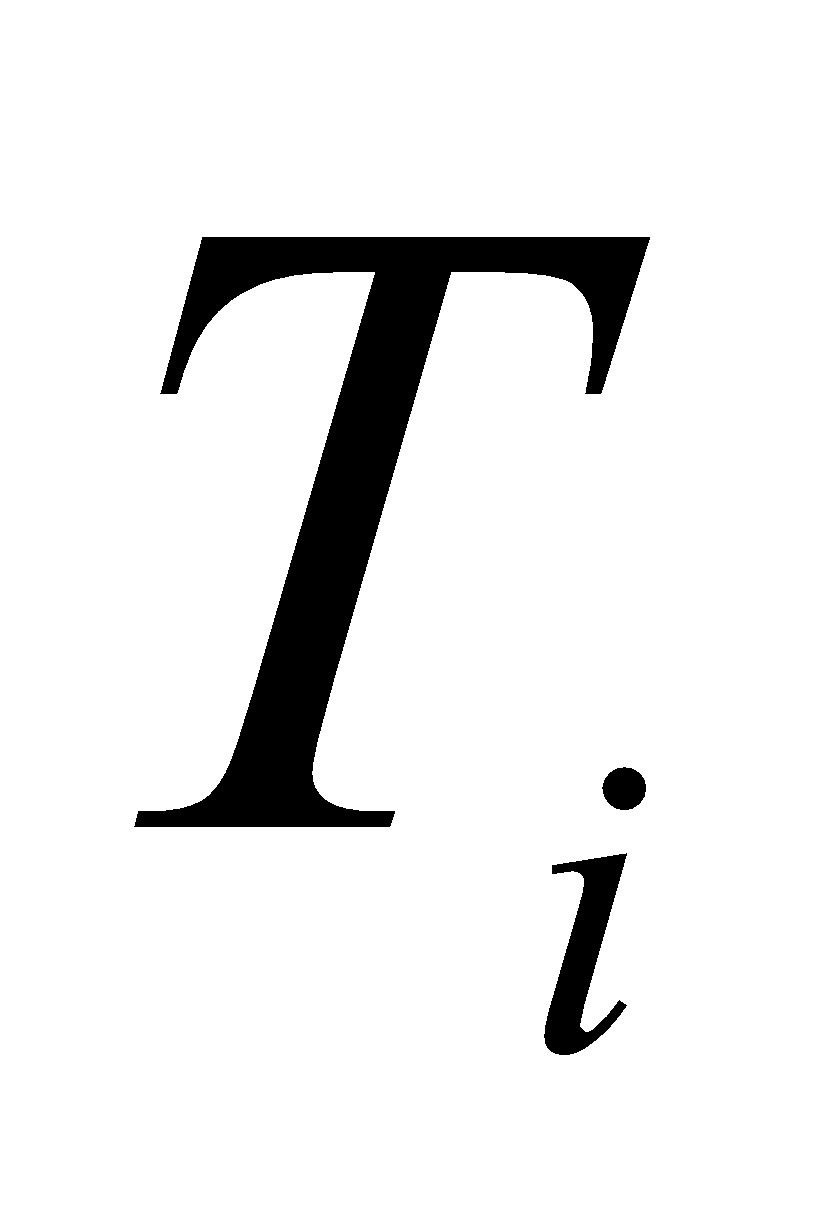
 через
через 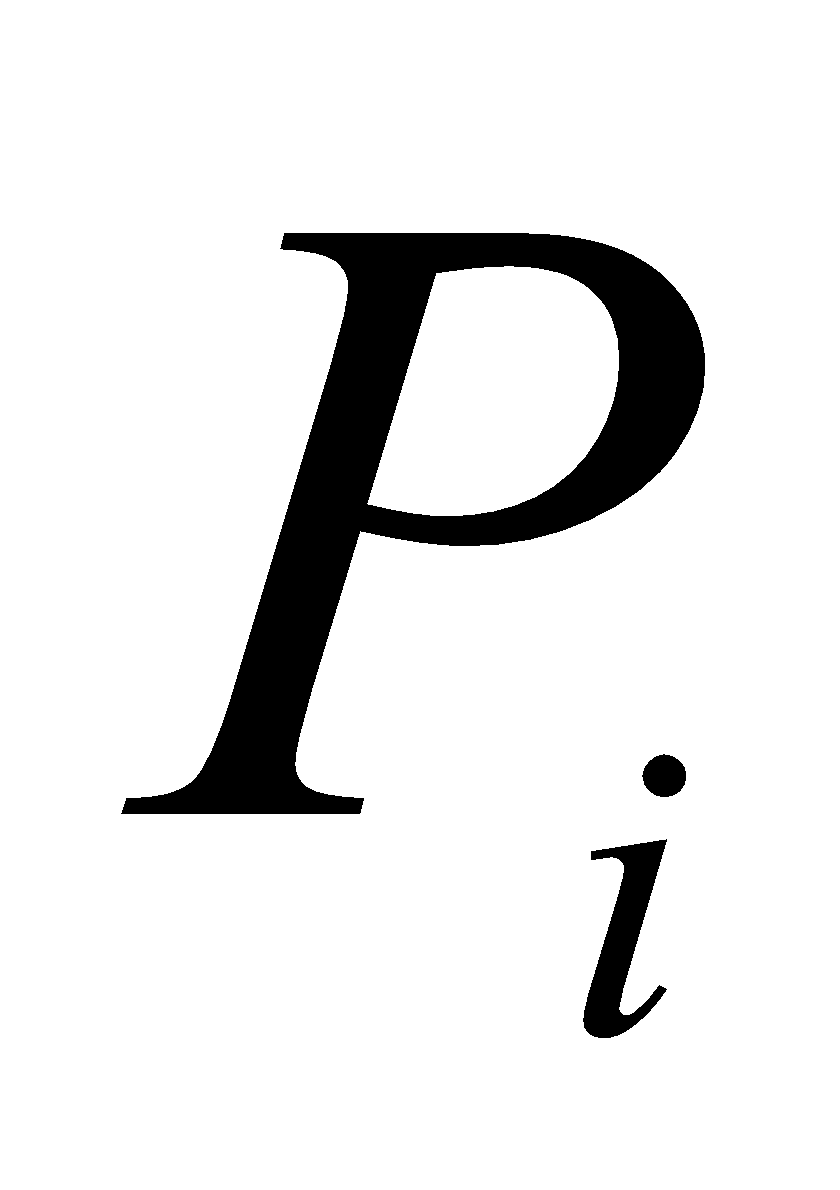
 , а функции принадлежности этой модели через
, а функции принадлежности этой модели через 
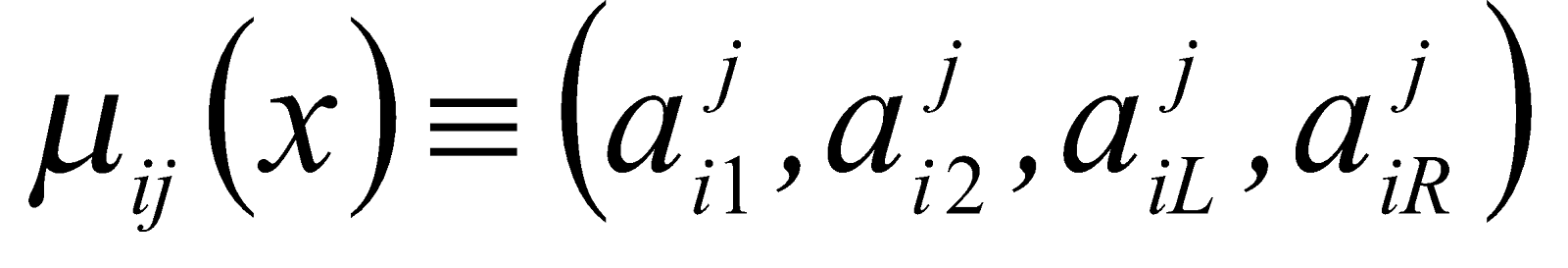 .
.
Обозначим через 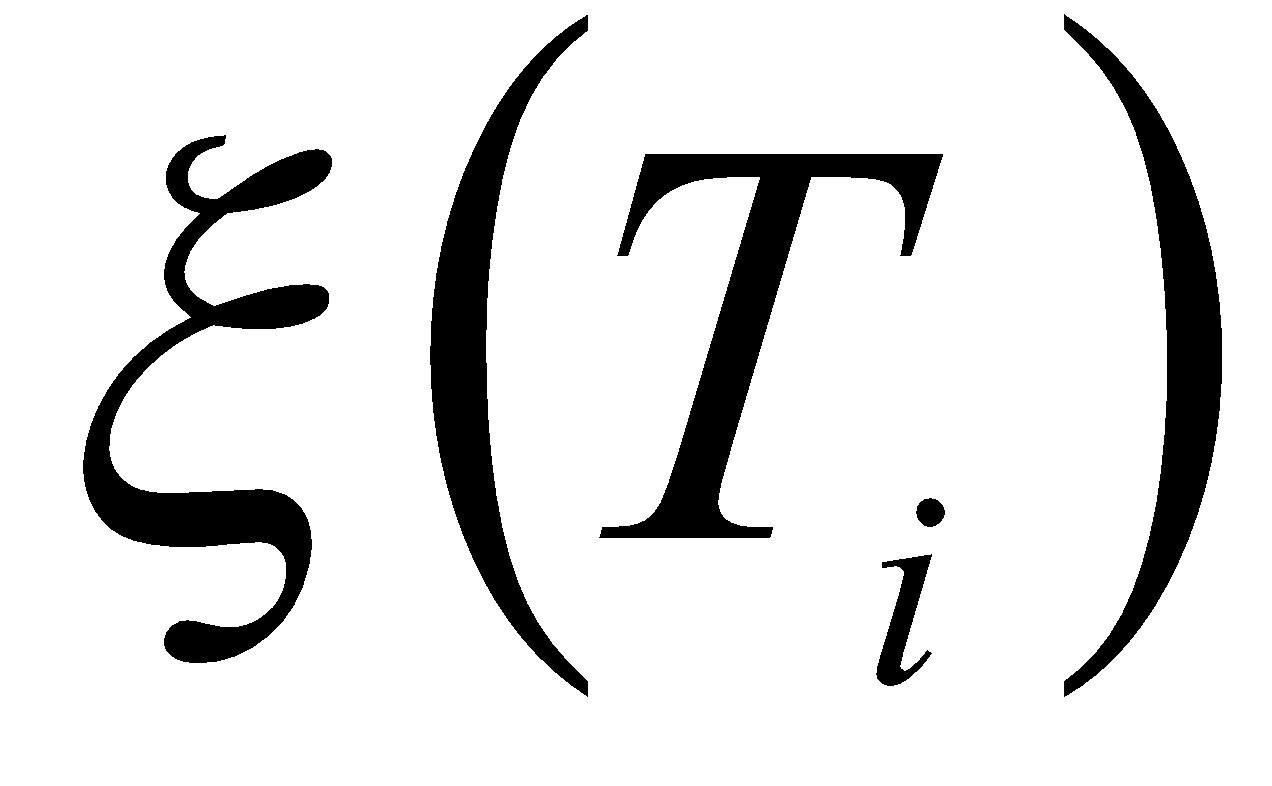
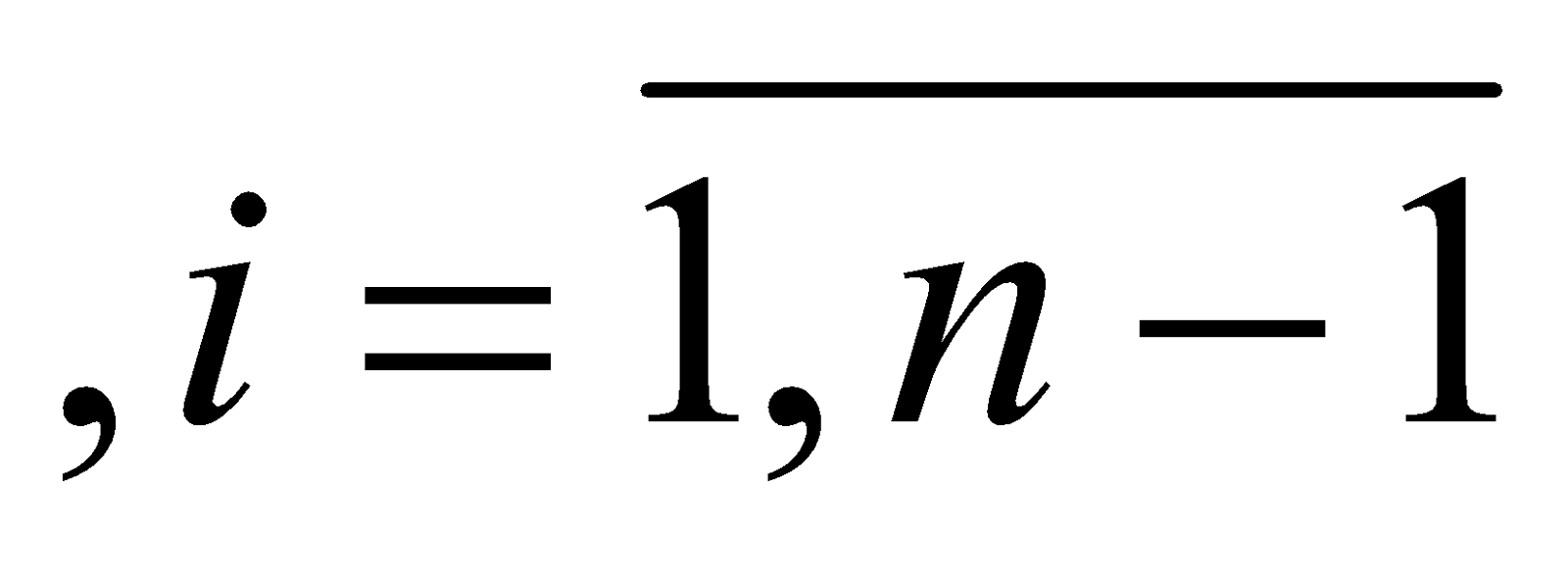

 - степень нечеткости модели
- степень нечеткости модели 
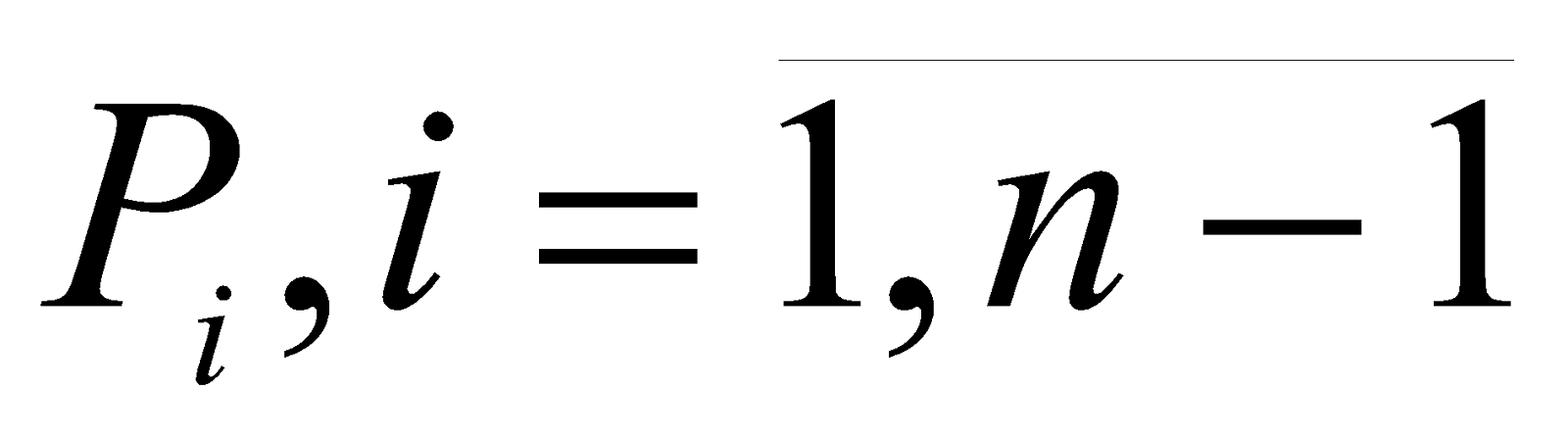 , а через
, а через 
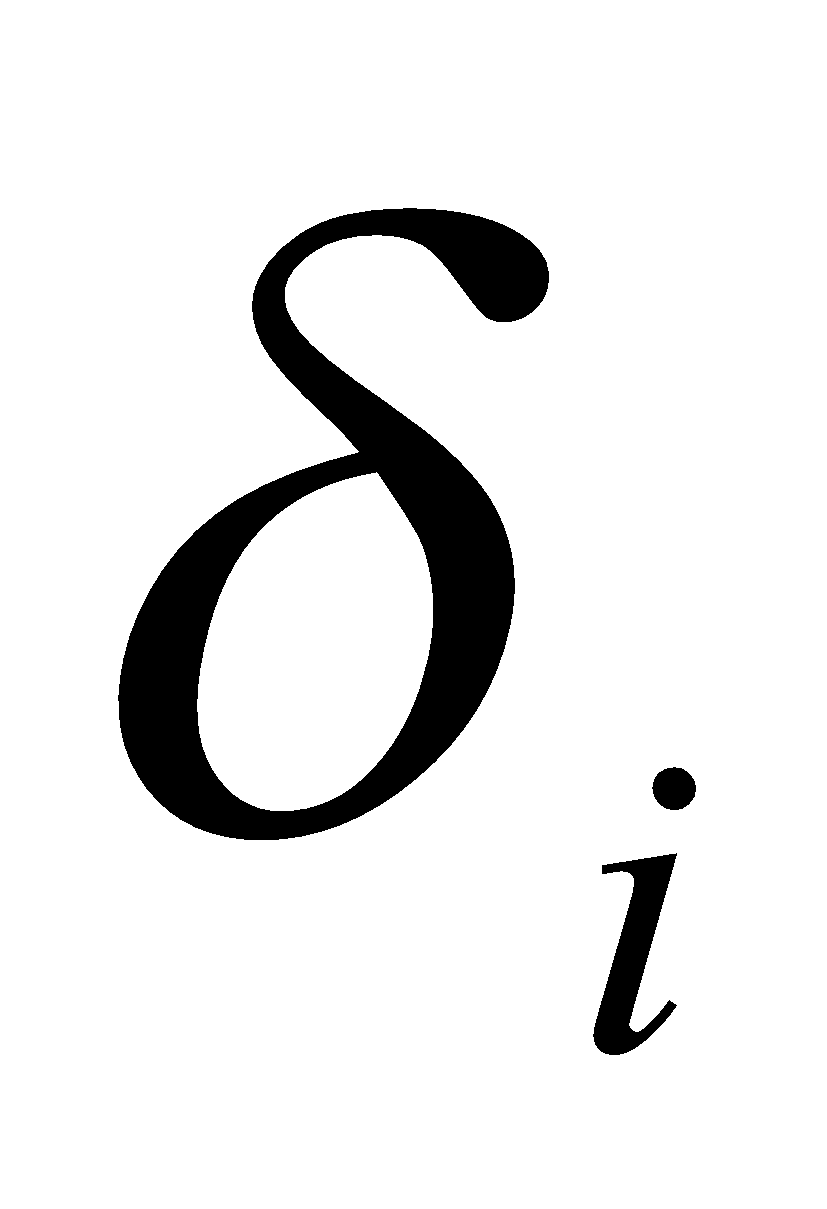 - показатель общей согласованности моделей
- показатель общей согласованности моделей 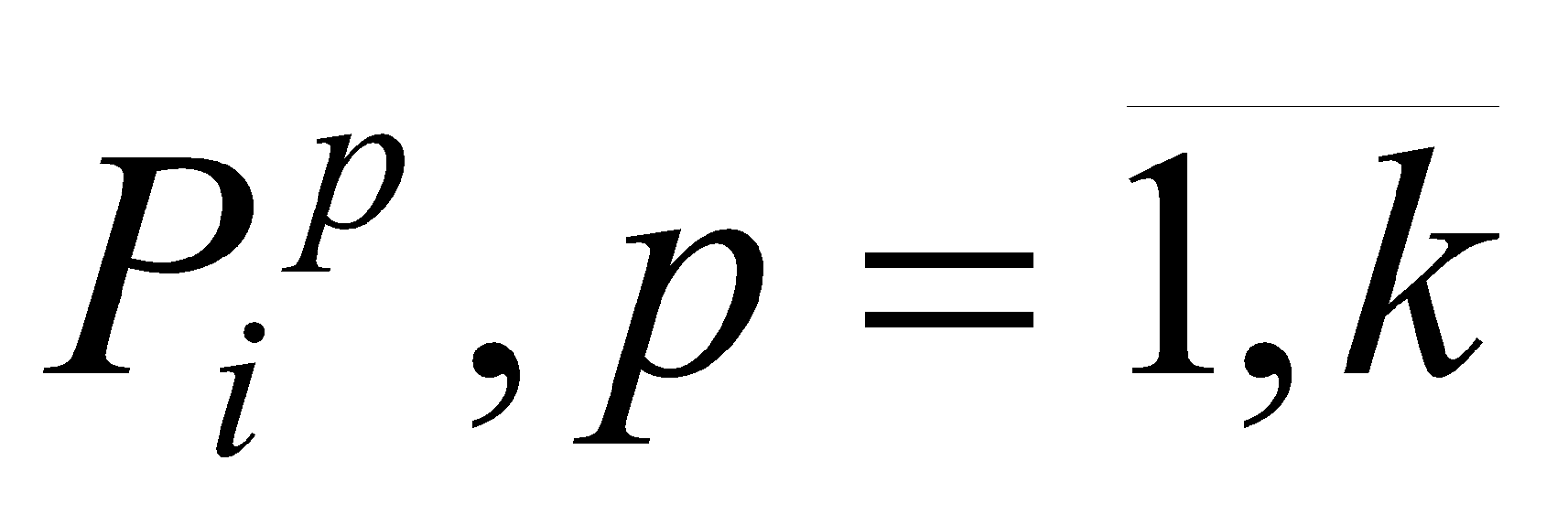
 .
.
Построим для показателя согласованности лингвистическую переменную с универсальным множеством  [0,1] и термами «низкий», «высокий», а для степени нечеткости лингвистическую переменную с универсальным множеством
[0,1] и термами «низкий», «высокий», а для степени нечеткости лингвистическую переменную с универсальным множеством  [0,0.5] и термами «малая», «большая».
[0,0.5] и термами «малая», «большая».
Вычислим в рамках всех множеств  T1,T2,...Tn-1 значения принадлежности степеней нечеткости обобщенных моделей к терму «малая» -
T1,T2,...Tn-1 значения принадлежности степеней нечеткости обобщенных моделей к терму «малая» - 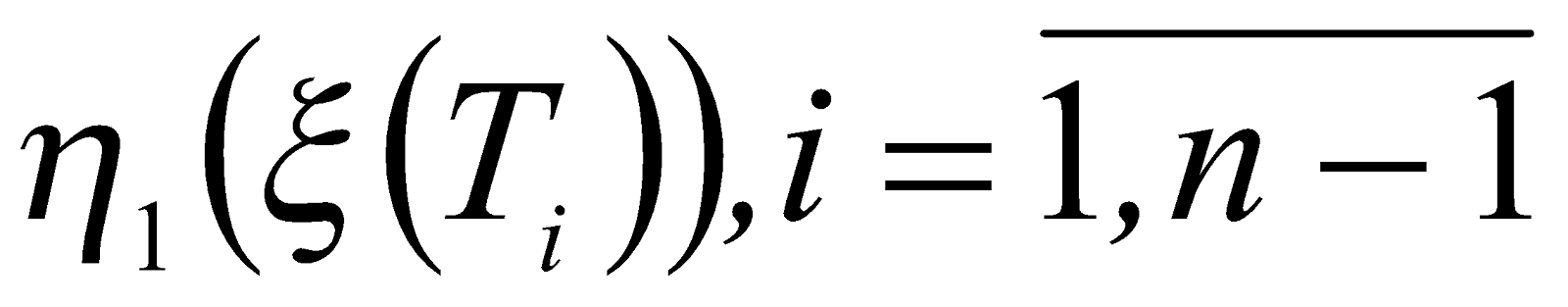
 и значения принадлежности показателей согласованности моделей экспертов к терму «высокий» -
и значения принадлежности показателей согласованности моделей экспертов к терму «высокий» - 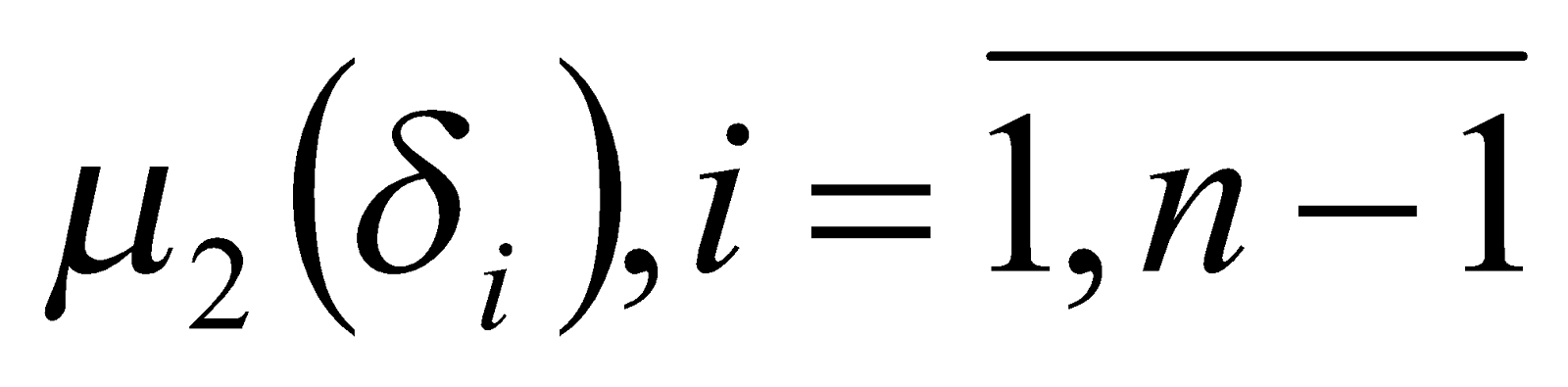
 .
.
Определим
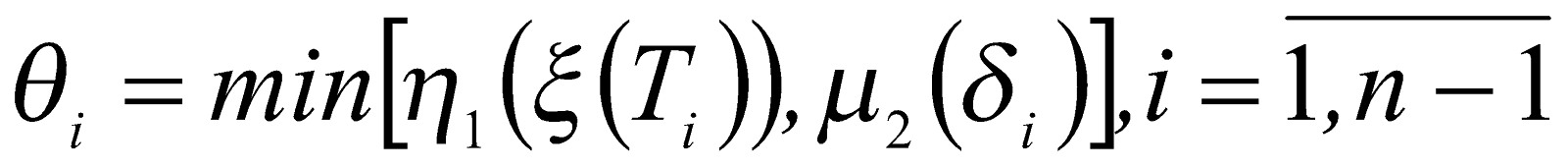
 .
.
Тогда множество 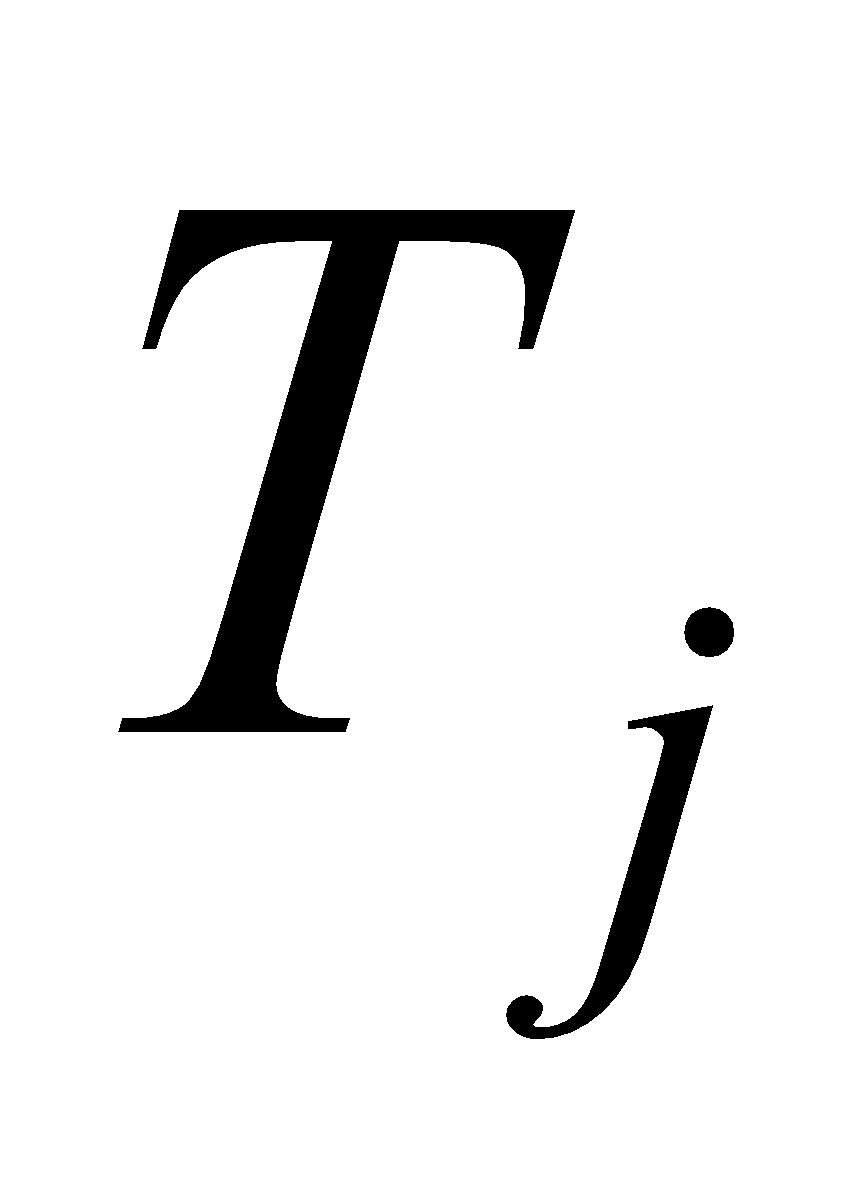
 лингвистической шкалы считается оптимальным множеством, если
лингвистической шкалы считается оптимальным множеством, если
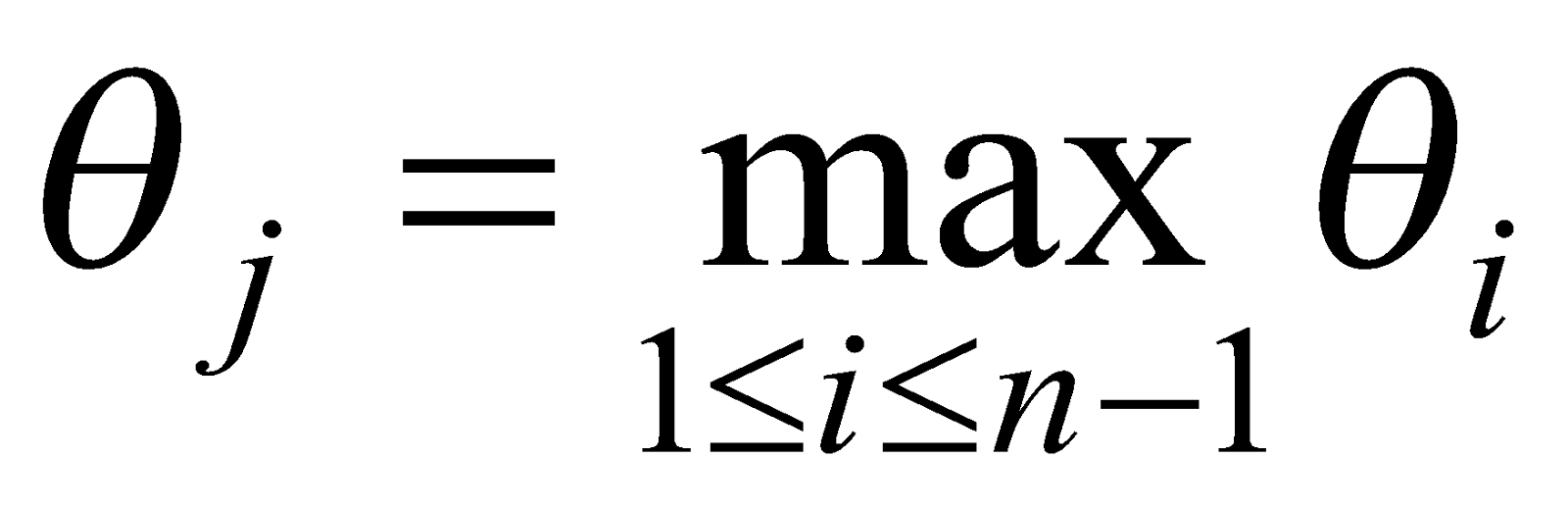
 .
.
Пусть в рамках ежегодного мониторинга получены познавательные психофизиологические характеристики (грамотность, точность восприятия, логичность мышления, пространственное воображение, скорость мыслительных процессов) для некоторой совокупности студентов. Характеристики оценивались в рамках вышеприведенной шкалы. Построим в пределах каждой характеристики лингвистическую переменную с количеством терм-множеств, равным количеству уровней вербально-числовой шкалы, используемой для оценивания характеристик [7].Обозначим за 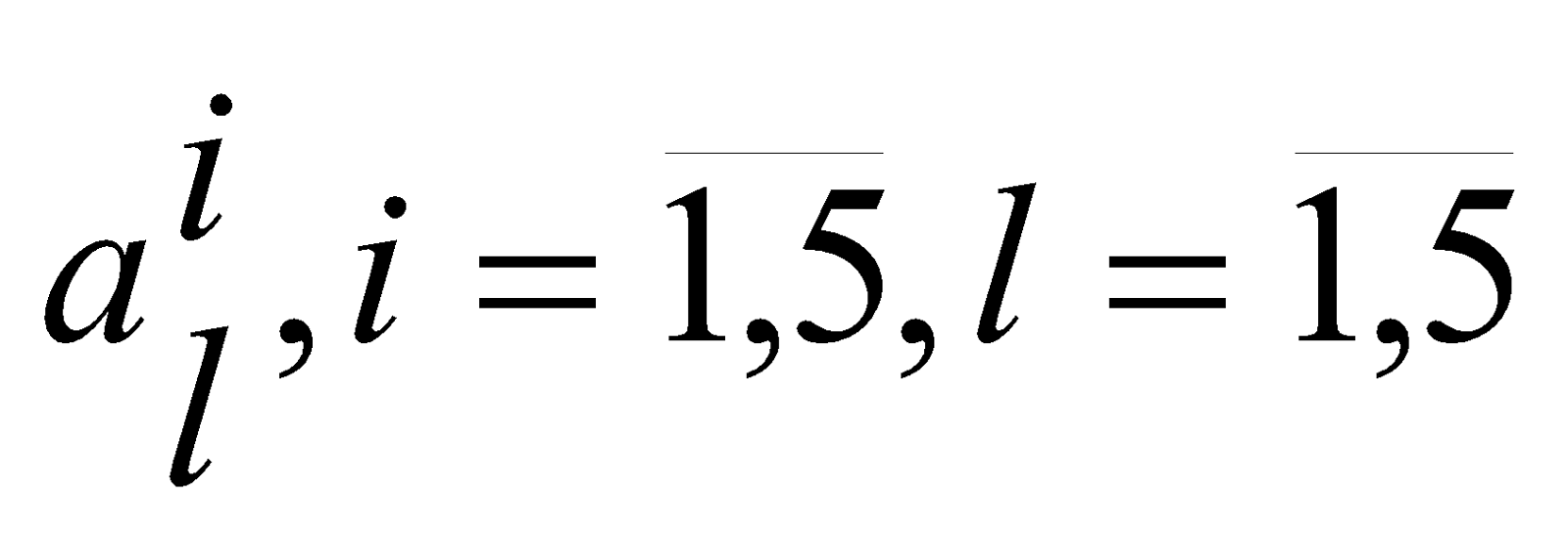
 относительное количество студентов, отнесенных к
относительное количество студентов, отнесенных к 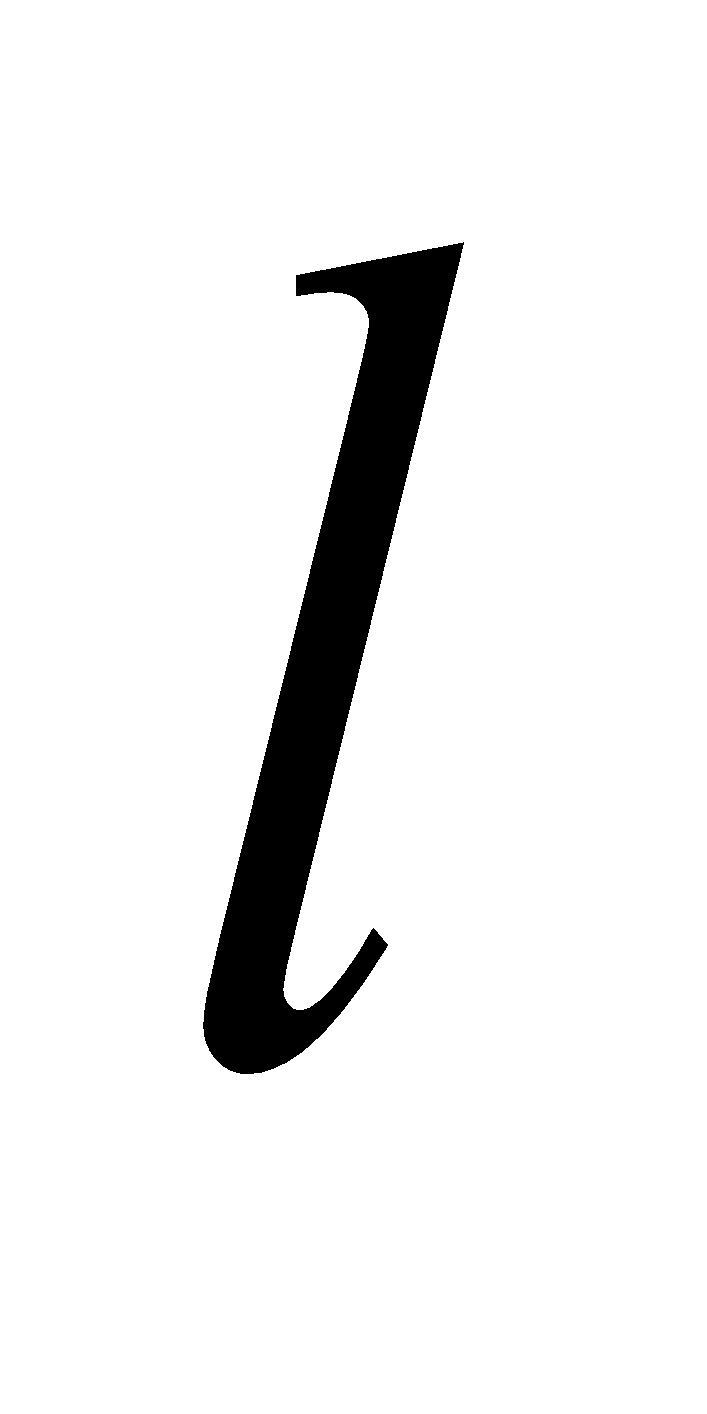
 -му уровню шкалы в рамках оценивания
-му уровню шкалы в рамках оценивания 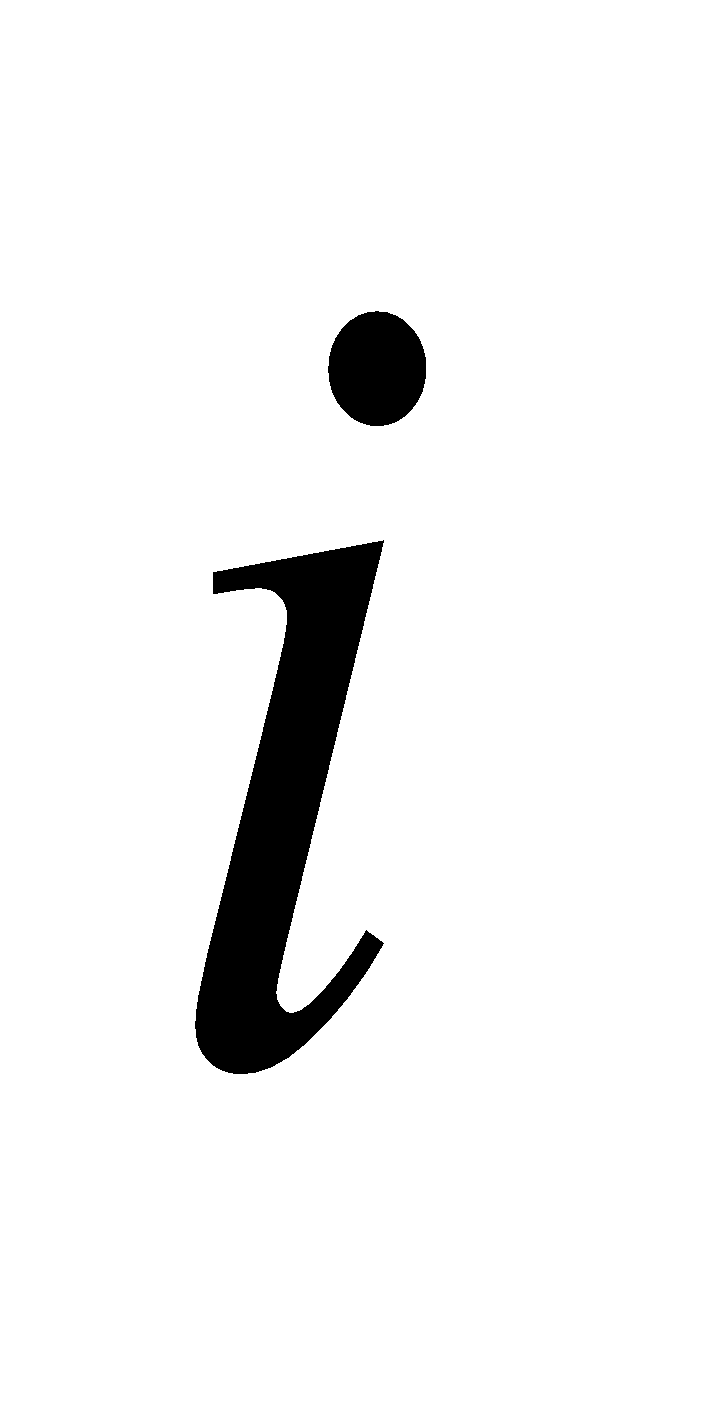
 -ой характеристики, а за
-ой характеристики, а за 
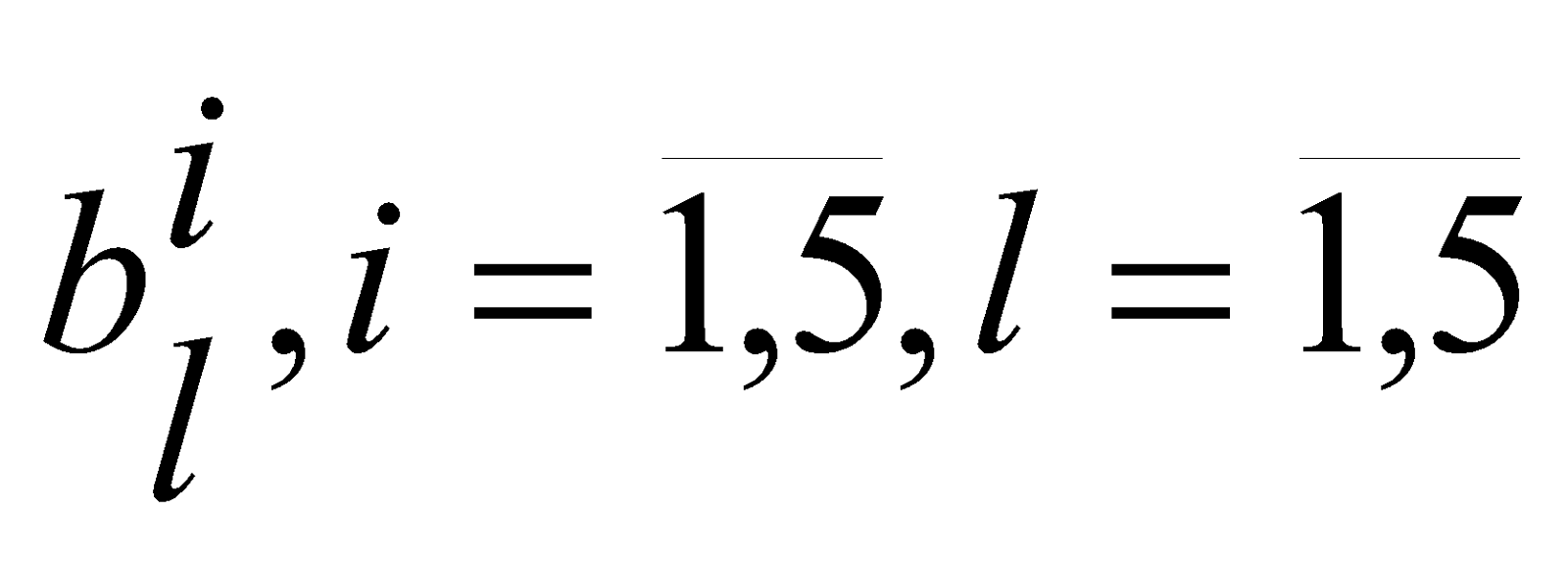 относительное количество студентов, отнесенных к
относительное количество студентов, отнесенных к 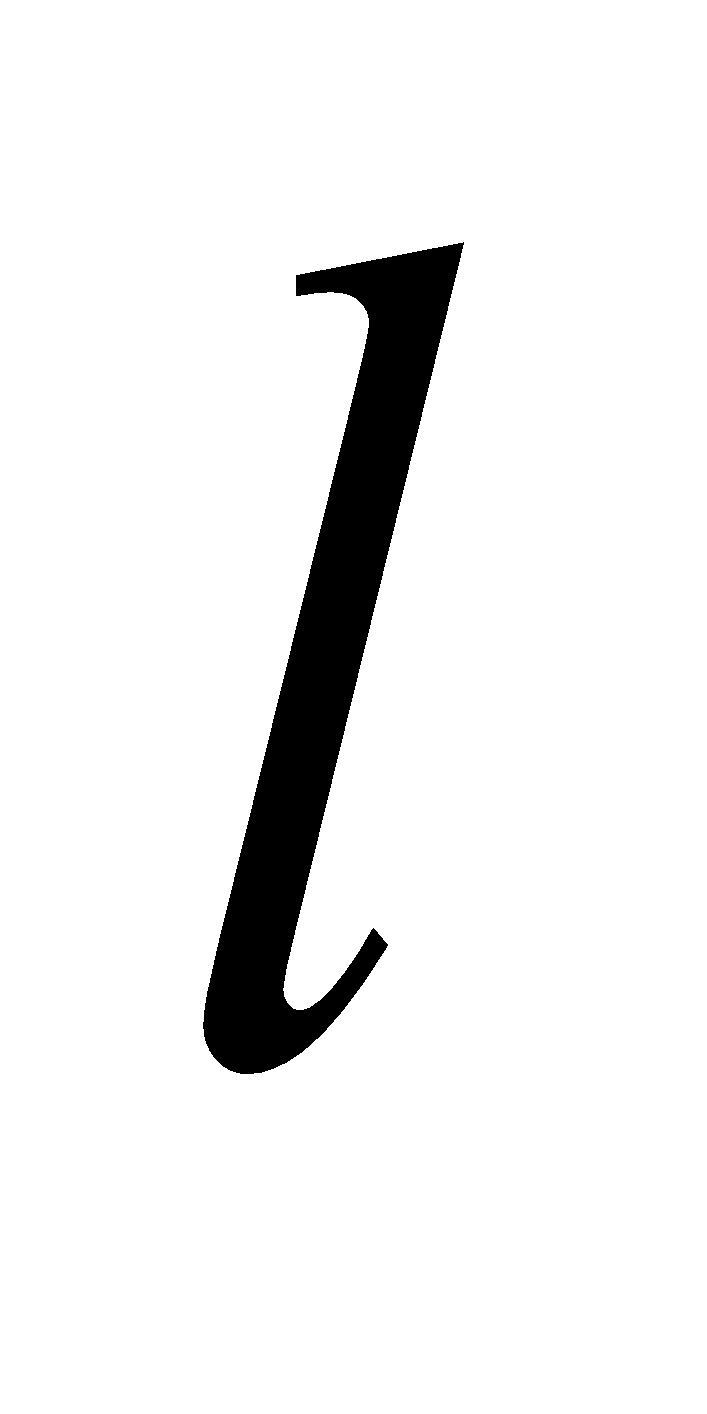
 -му уровню шкалы в рамках оценивания
-му уровню шкалы в рамках оценивания 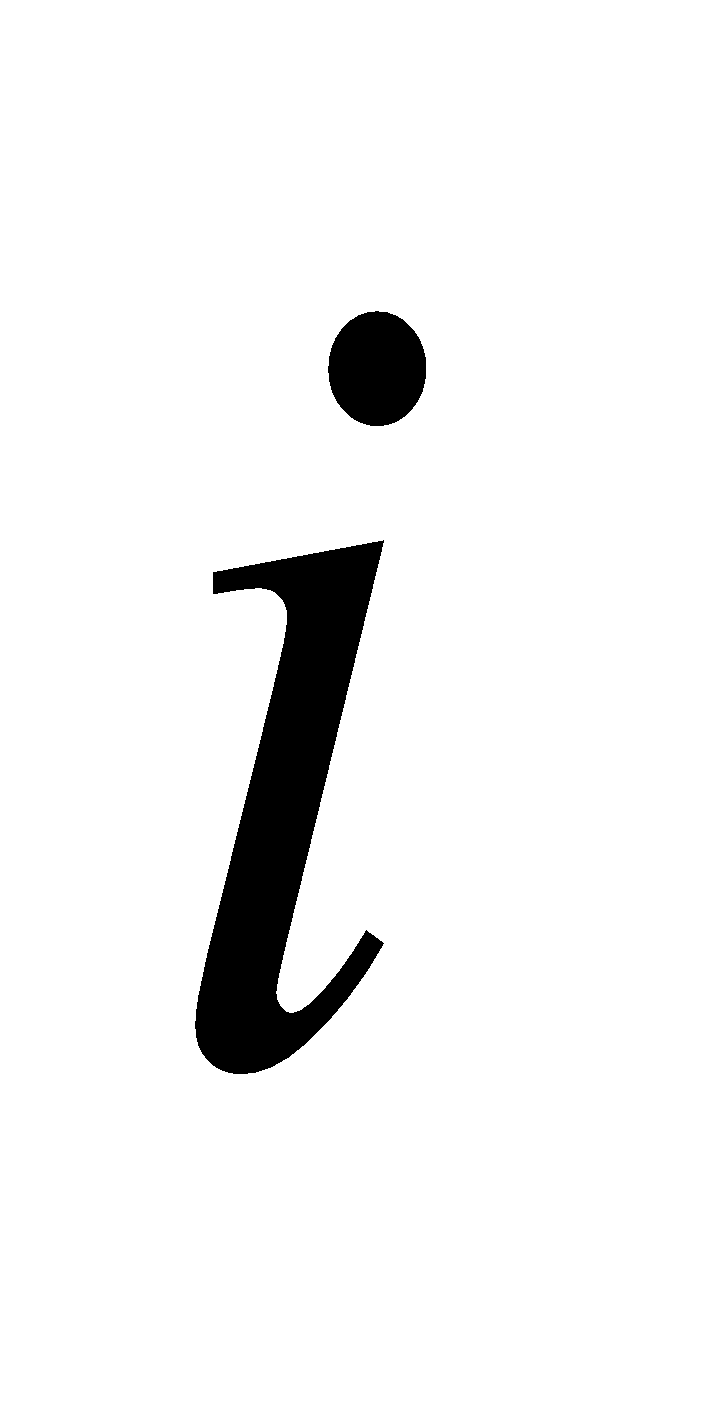
 -ой характеристики, не ограничивая общности, через год. Обозначим за
-ой характеристики, не ограничивая общности, через год. Обозначим за 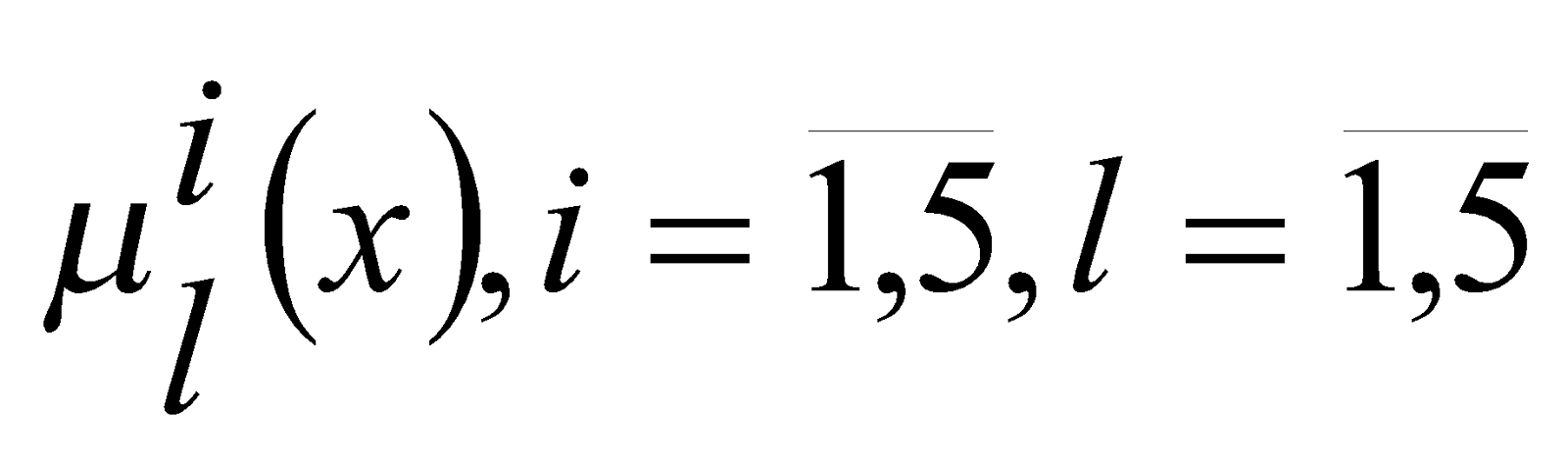
 - функции принадлежности терм-множеств пяти лингвистических переменных, построенных в рамках метода [6,8] и общих данных за два года оценивания. Определим общие нечеткие рейтинговые оценки познавательных психофизиологических характеристик следующим образом
- функции принадлежности терм-множеств пяти лингвистических переменных, построенных в рамках метода [6,8] и общих данных за два года оценивания. Определим общие нечеткие рейтинговые оценки познавательных психофизиологических характеристик следующим образом
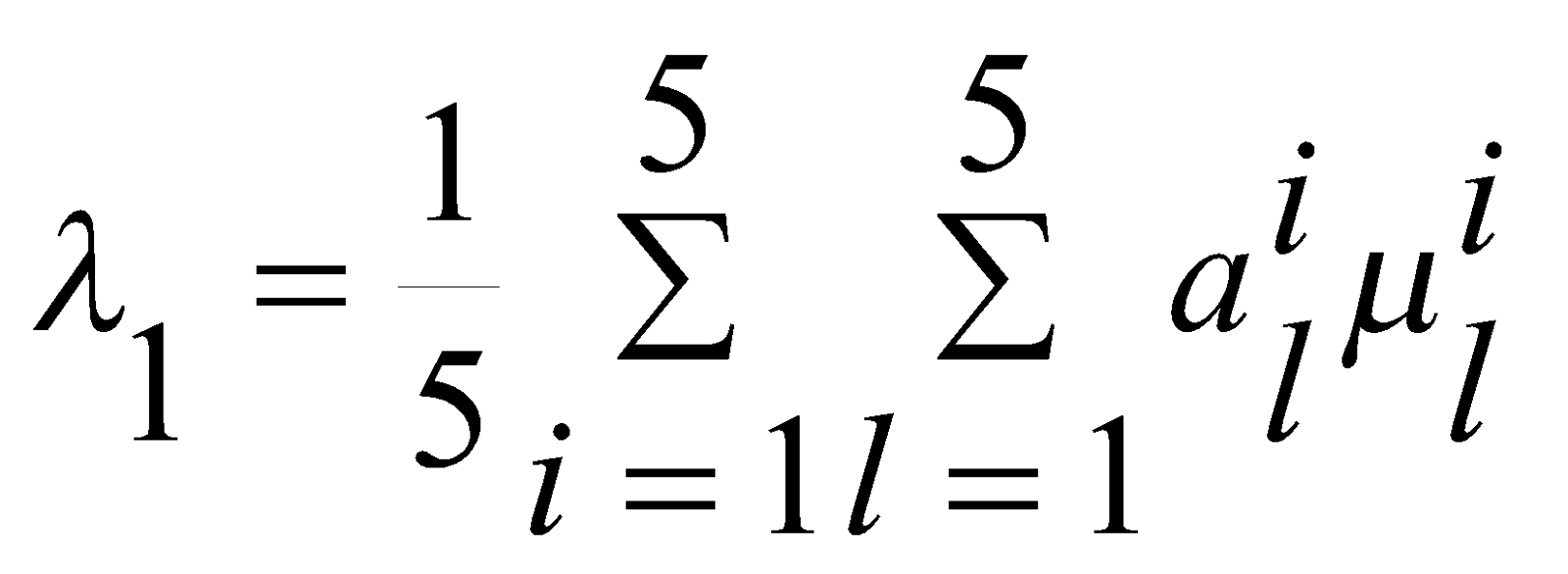
 ,
,
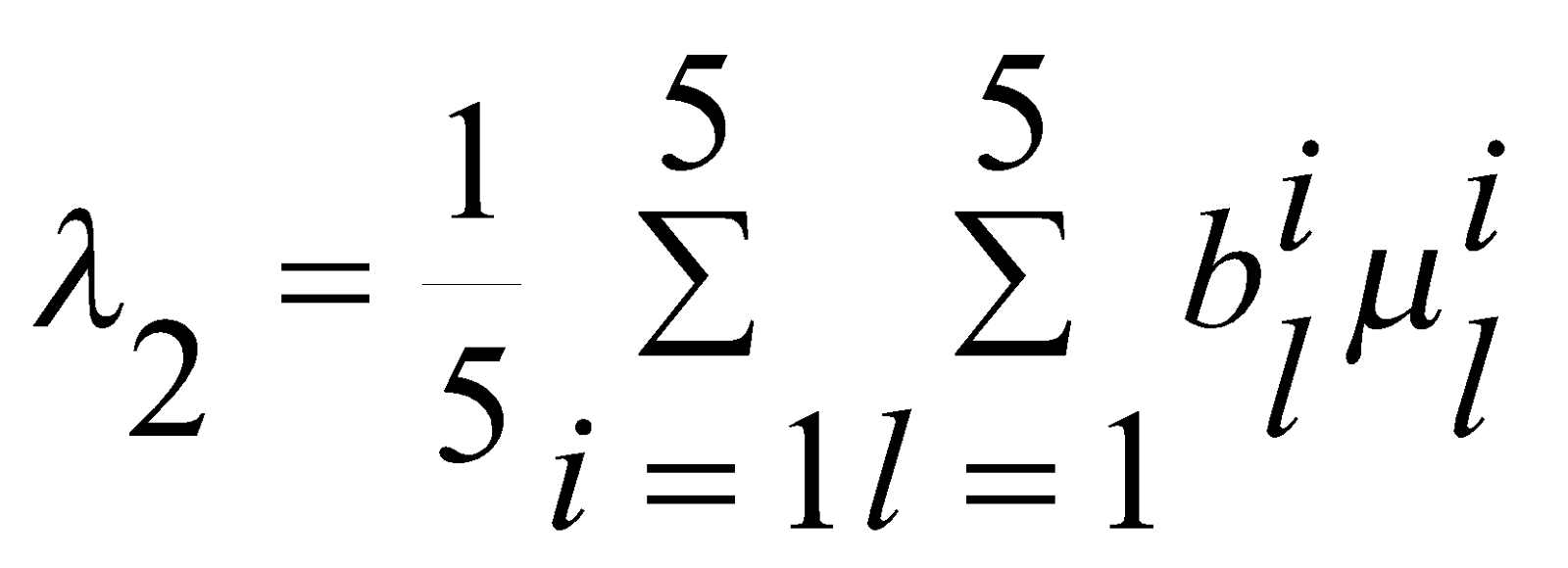
 .
.
Количественные рейтинговые оценки находятся, например, широко применяемым методом центра тяжести и называются средними степенями проявления познавательных психофизиологических характеристик. На основе анализа этих оценок в дополнение к анализу показателей успеваемости делаются выводы о качестве образовательного процесса.
Пример. Рассмотрим данные оценивания логичности мышления и скорости мыслительных процессов студентов: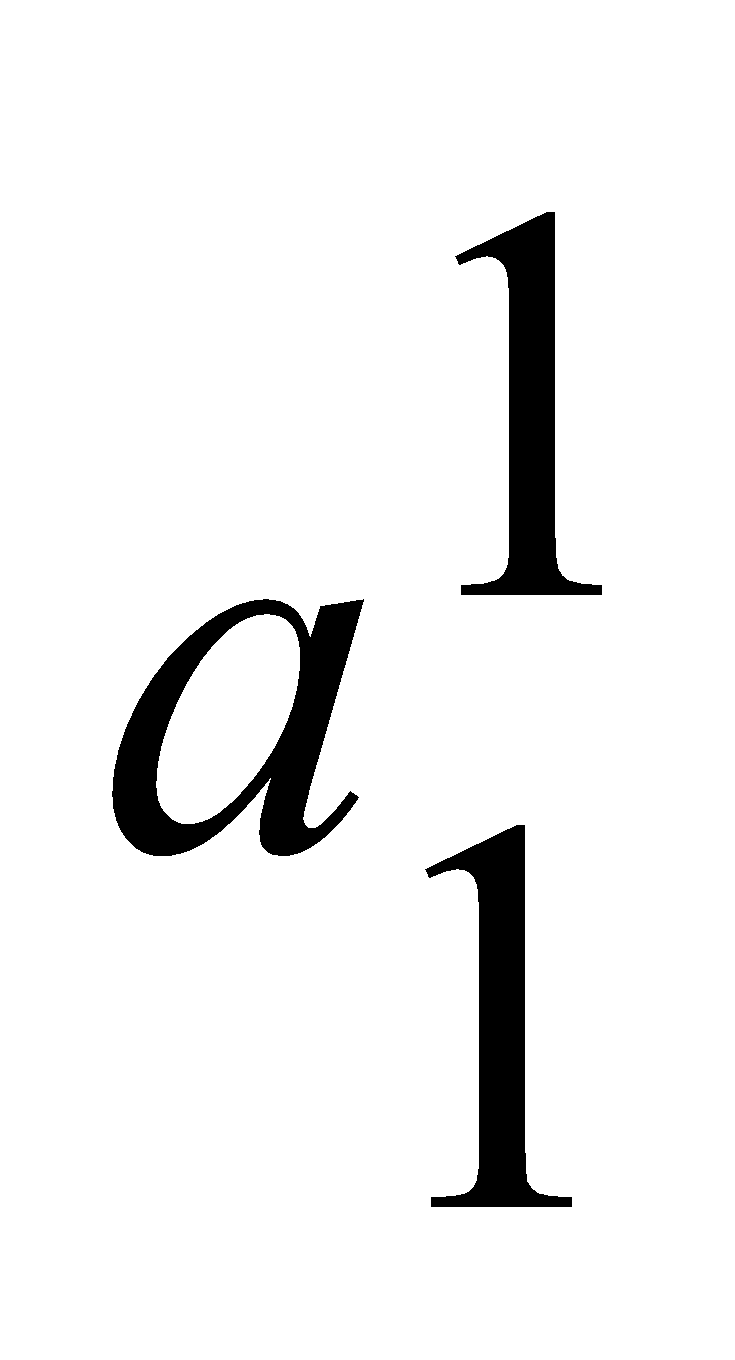
 =0.2,
=0.2, 
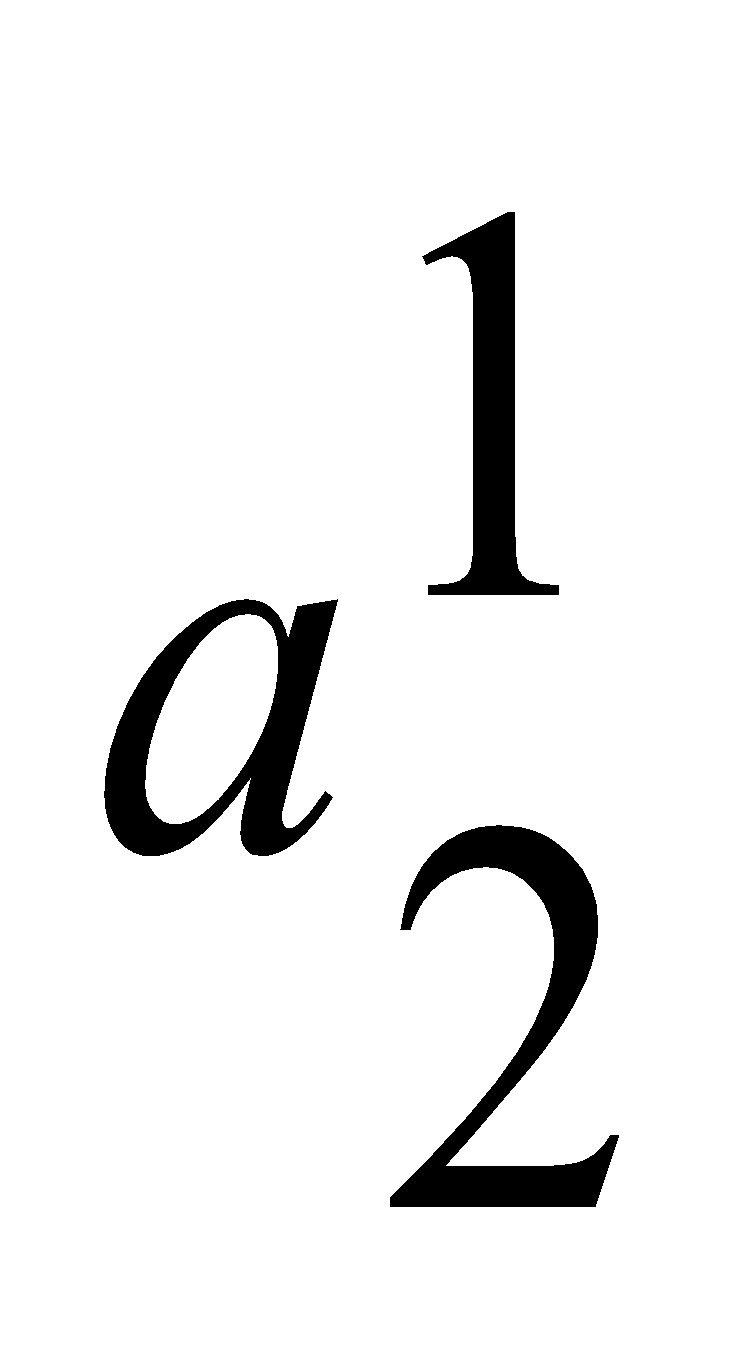 =0.21,
=0.21, 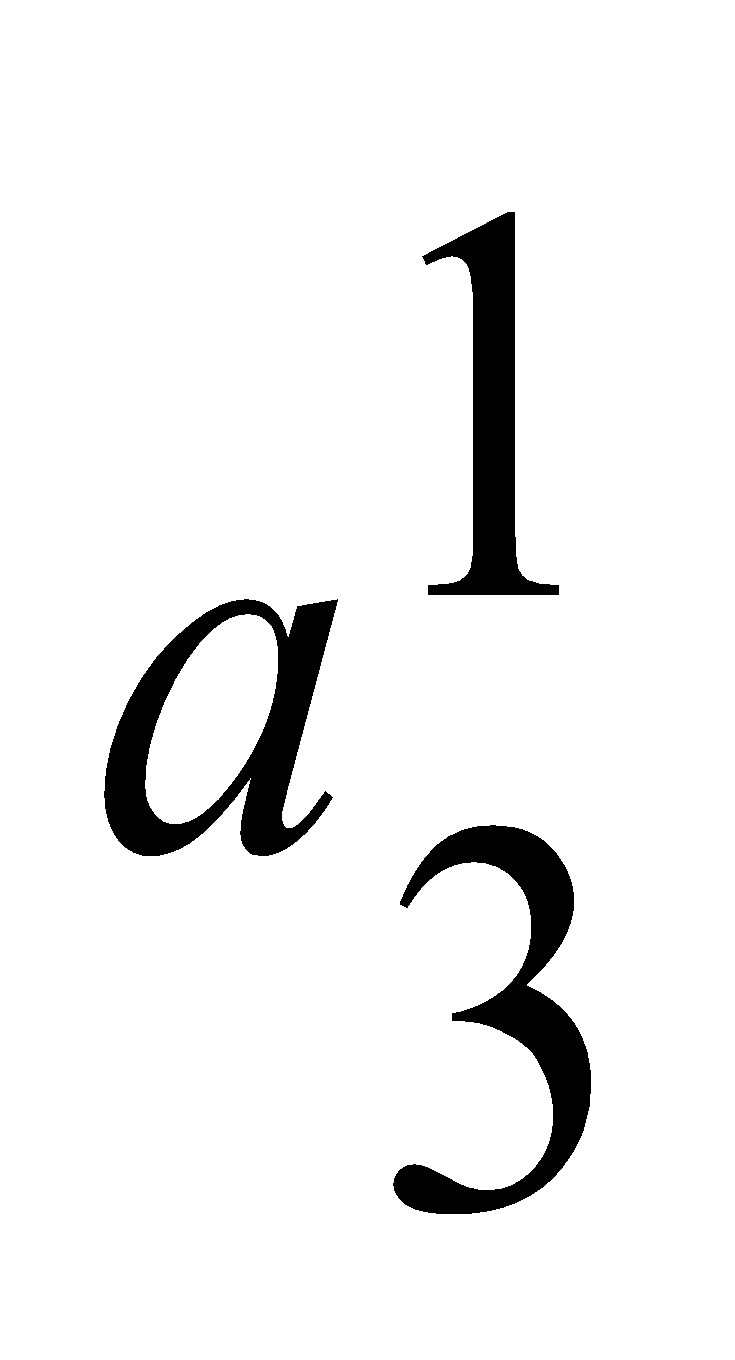
 =0.37,
=0.37, 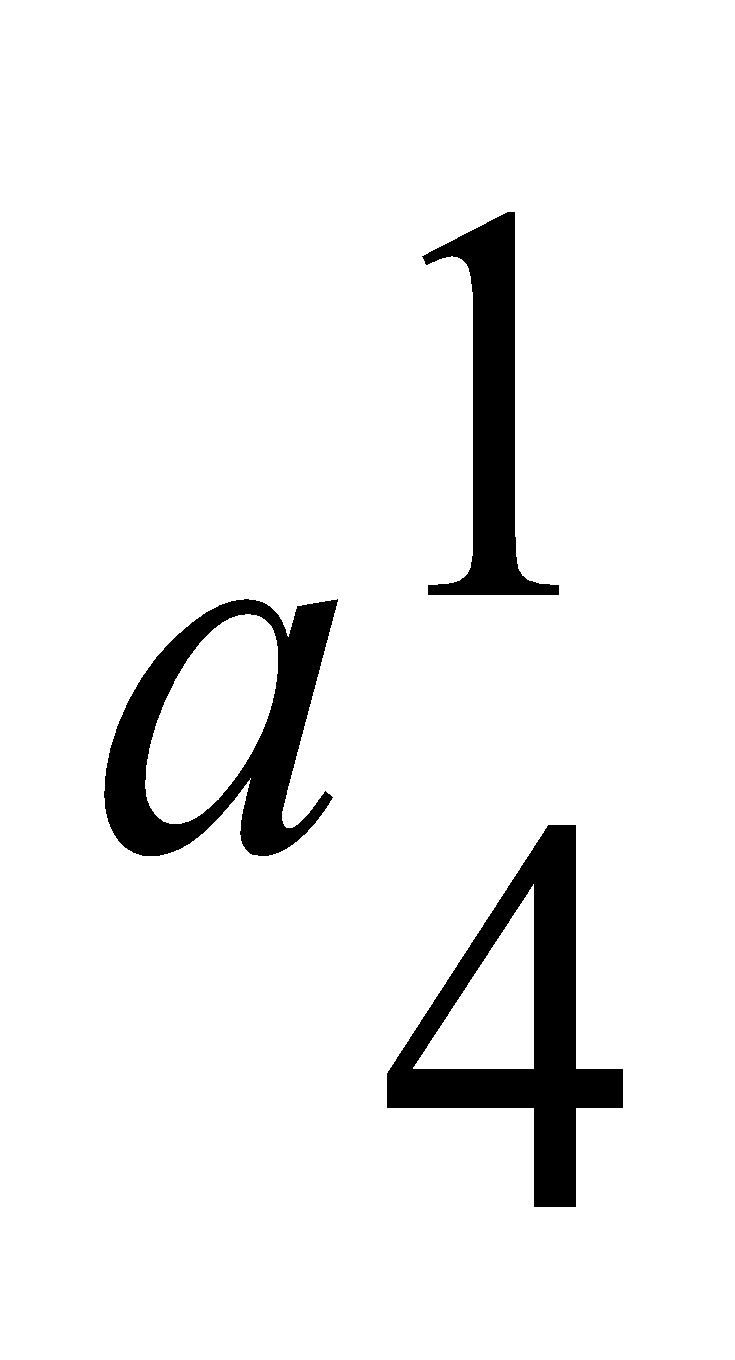
 =0.22,
=0.22, 
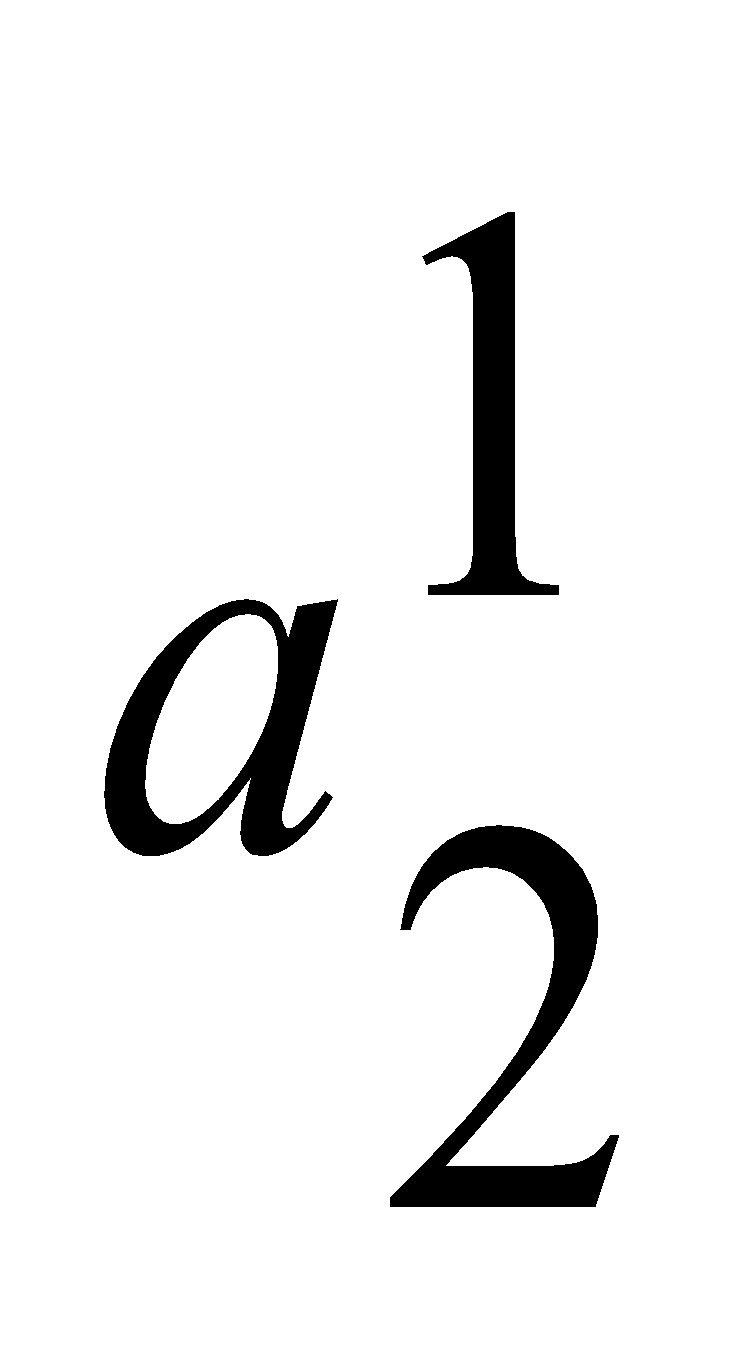 =0.12,
=0.12, 
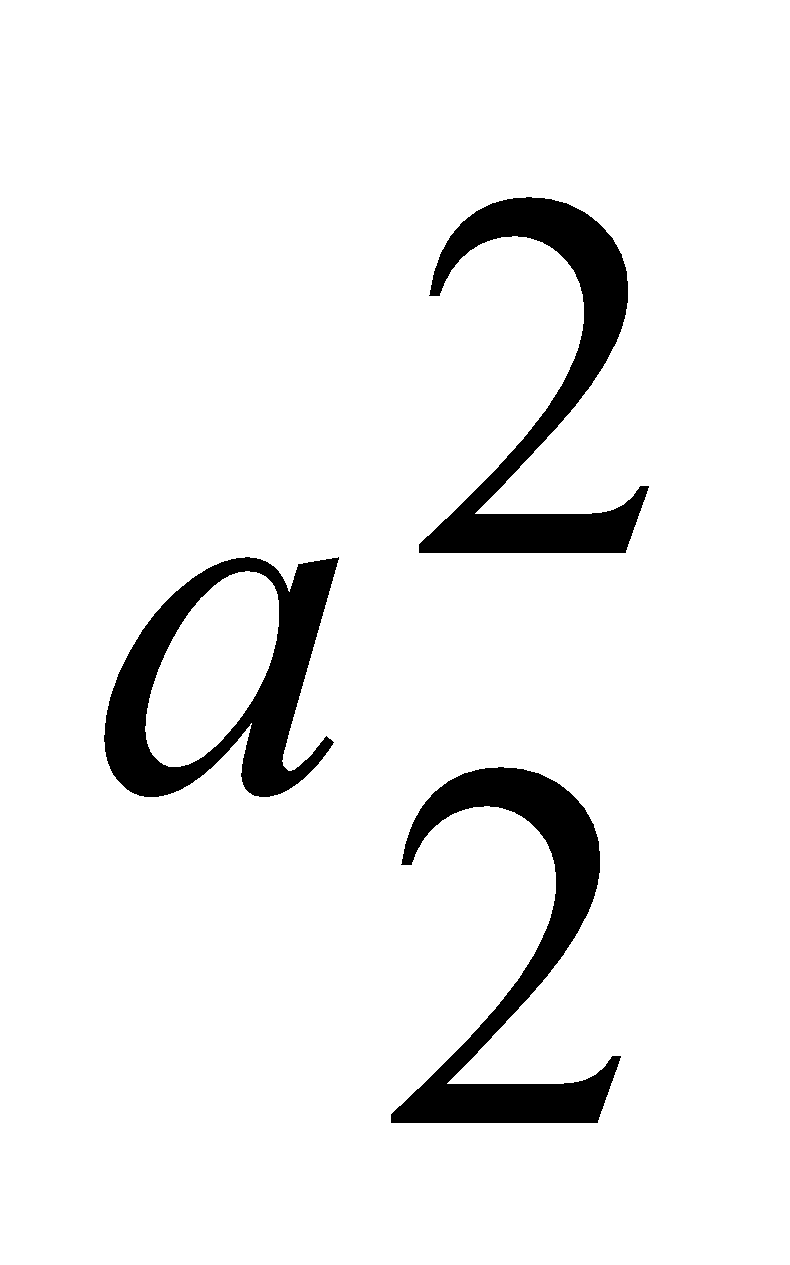 =0.08,
=0.08, 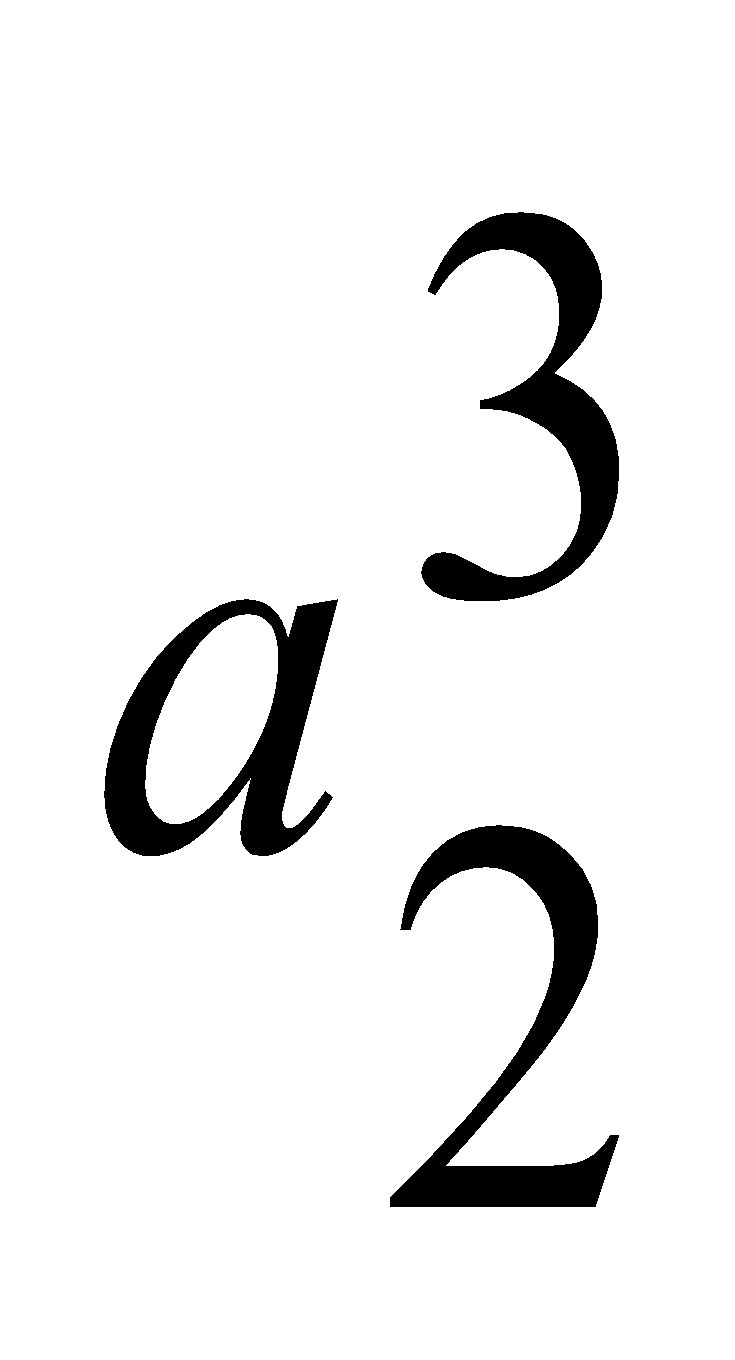
 =0.45,
=0.45, 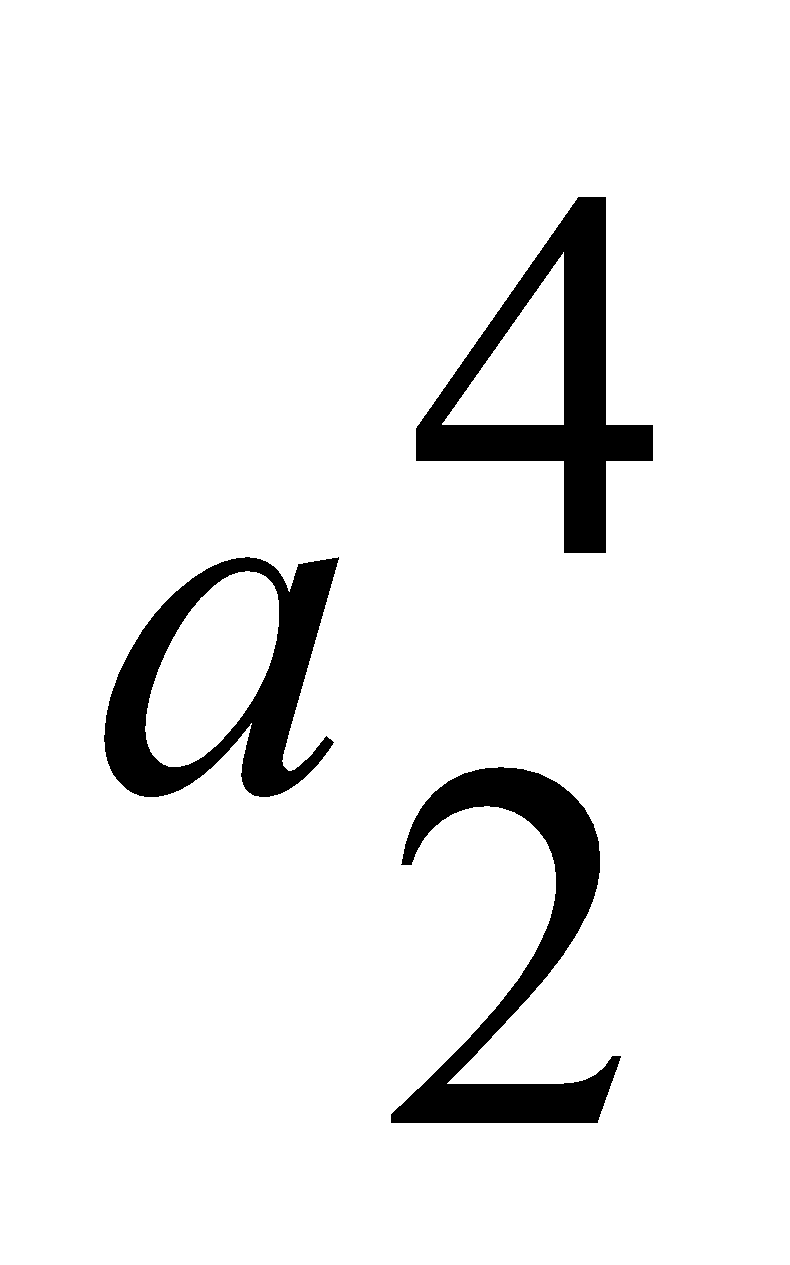
 =0.35,
=0.35, 
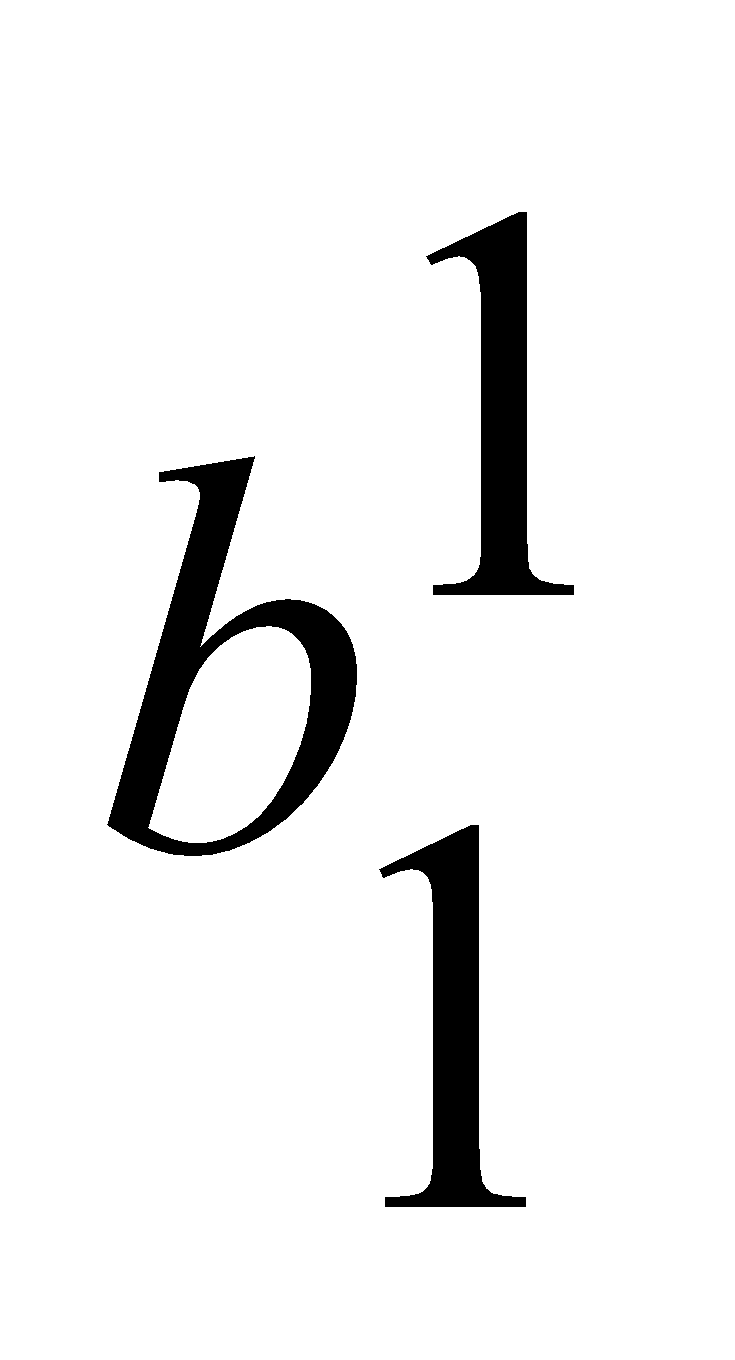 =0.05,
=0.05, 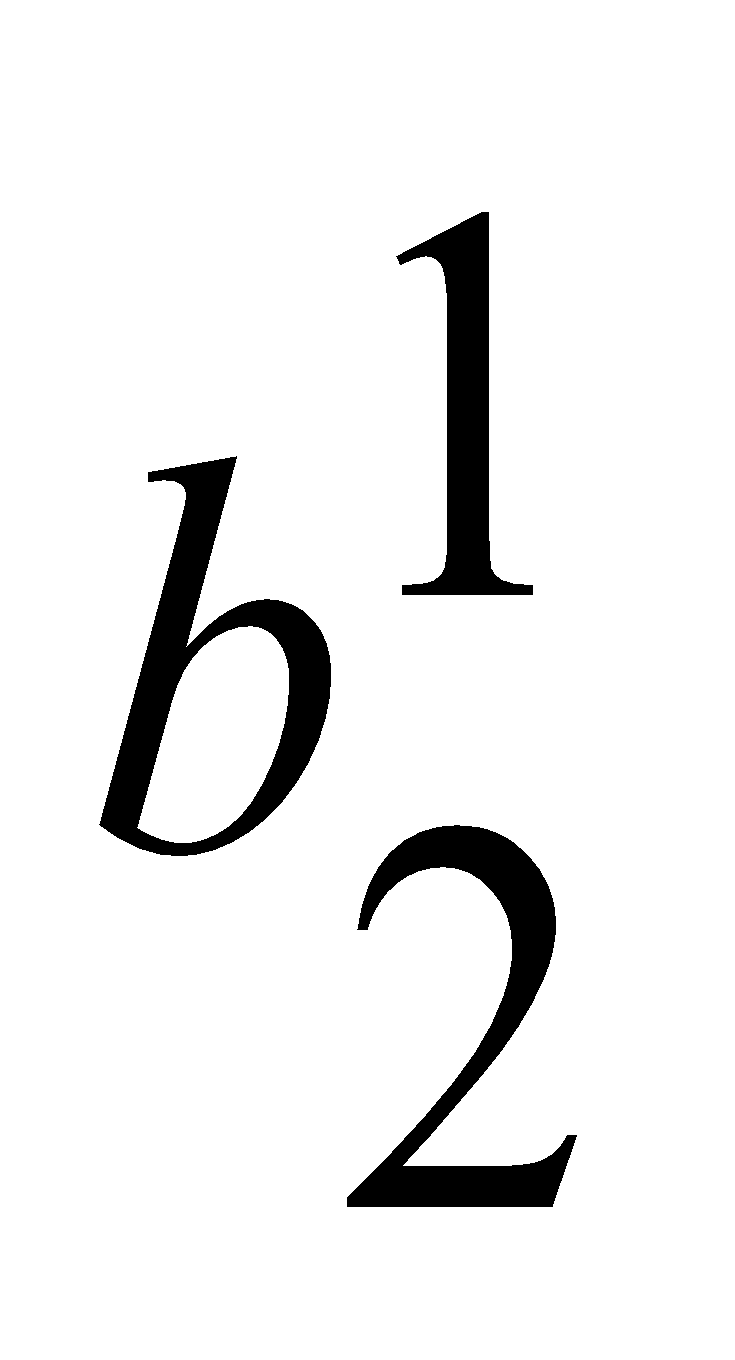
 =0.26,
=0.26, 
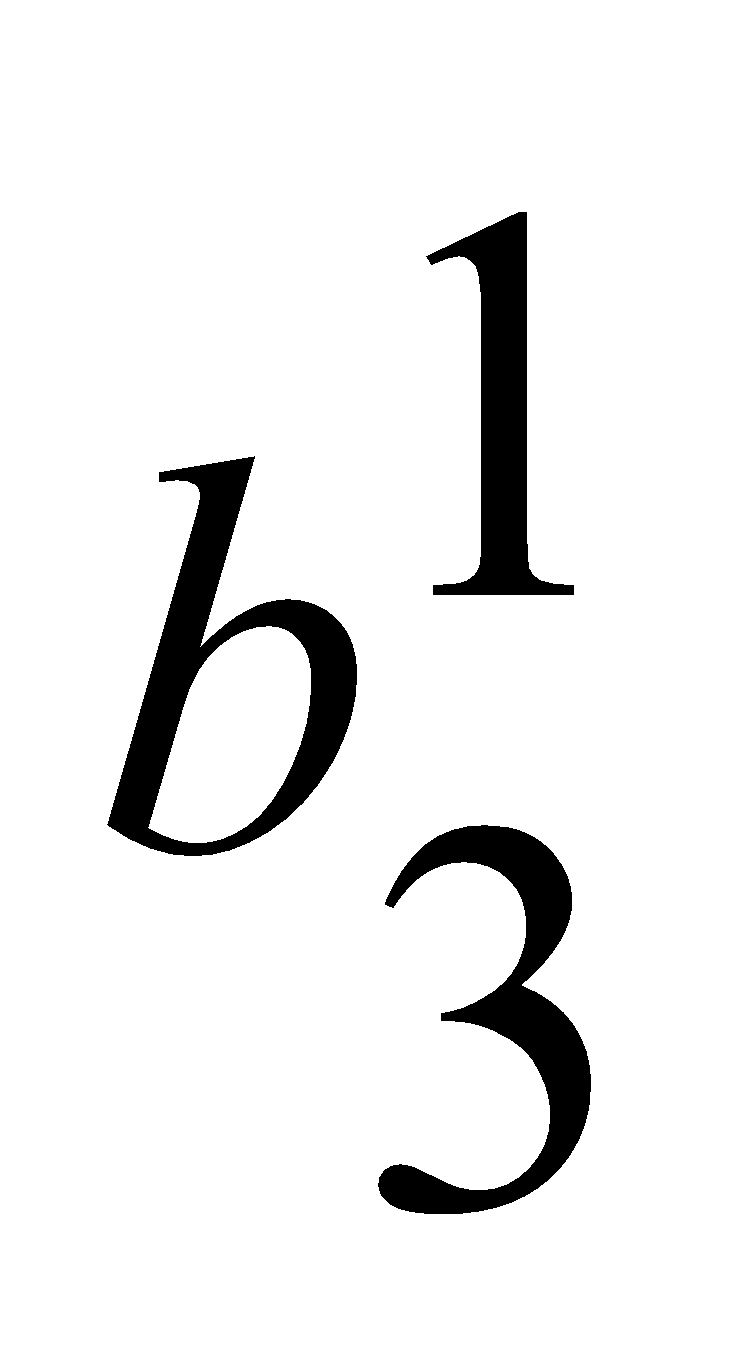 =0.41,
=0.41, 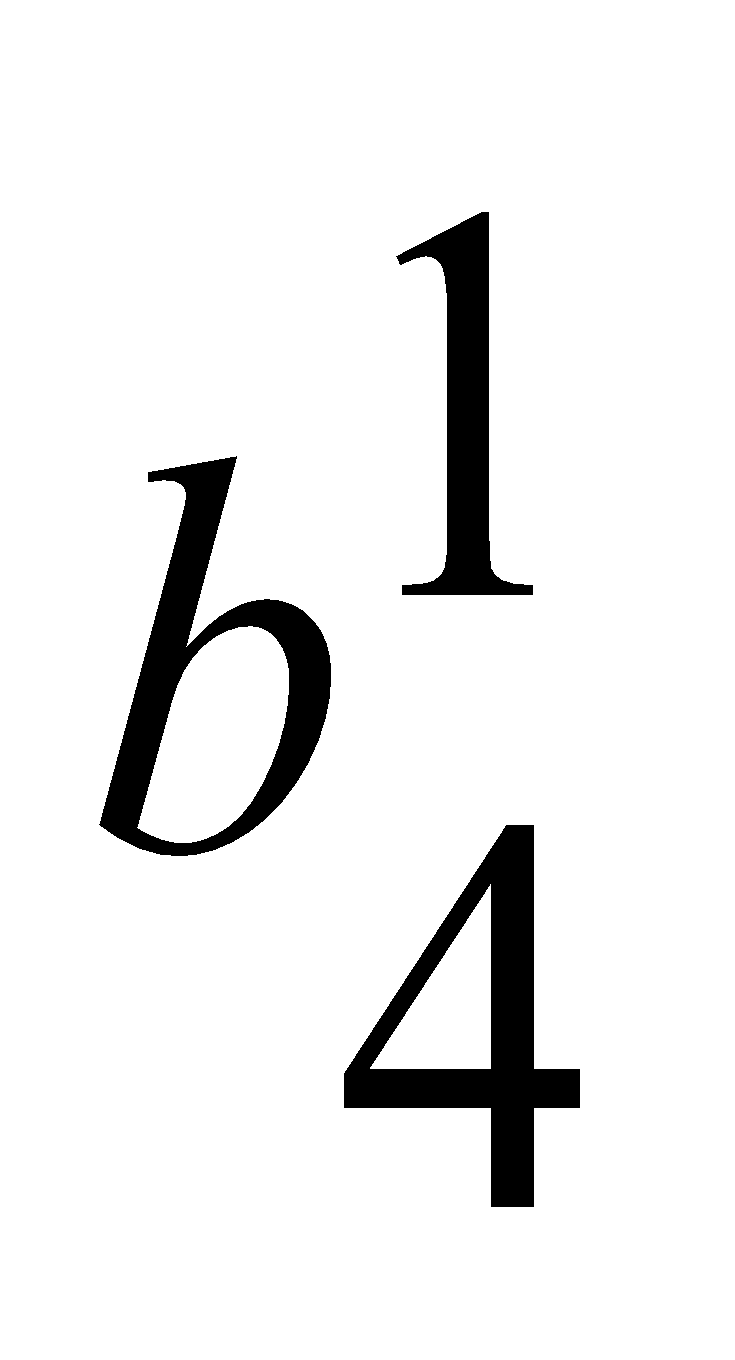
 =0.28,
=0.28, 
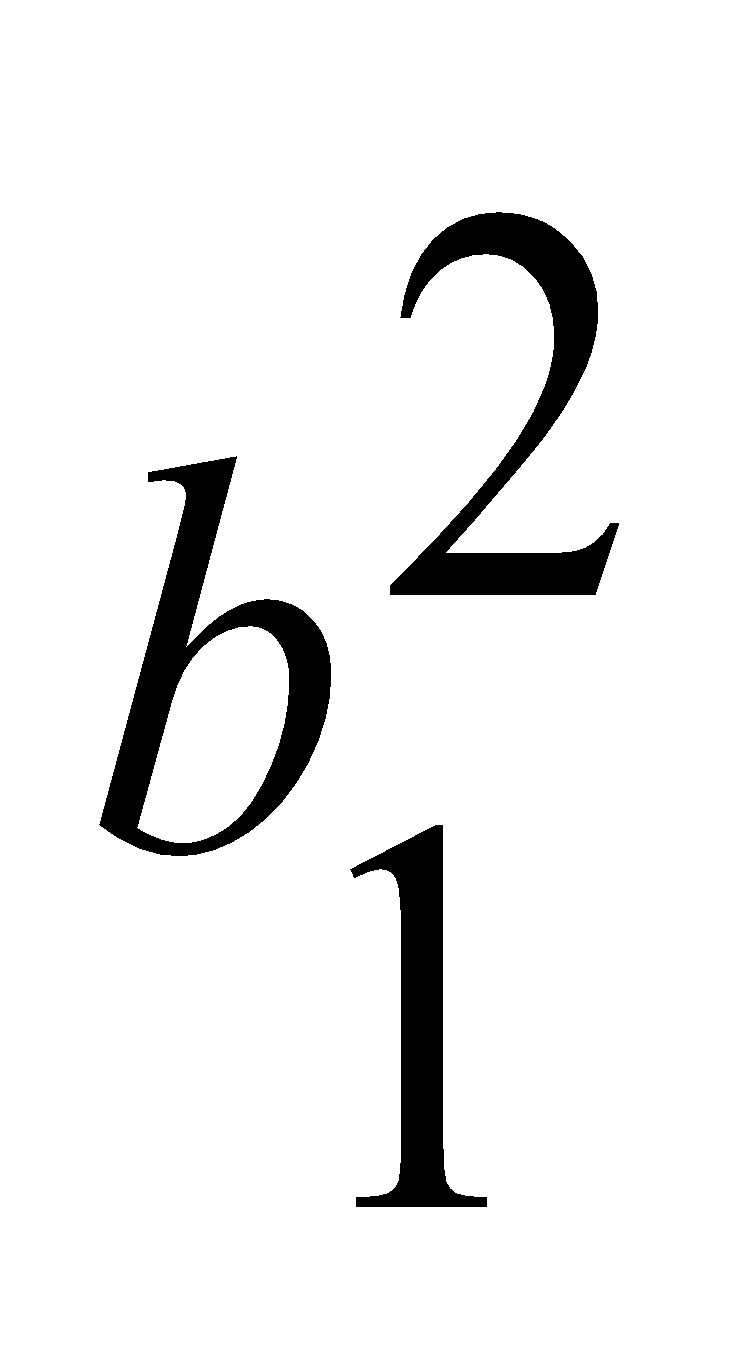 =0.04,
=0.04, 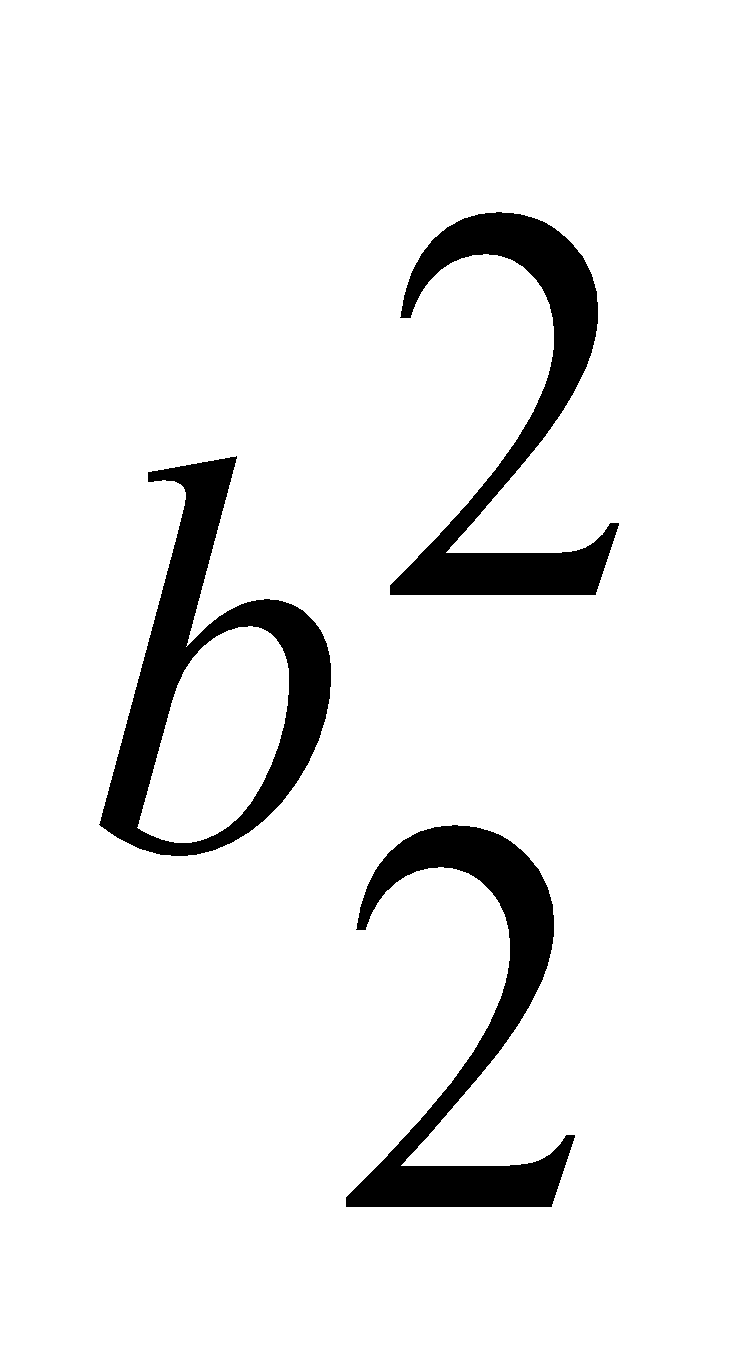
 =0.03,
=0.03, 
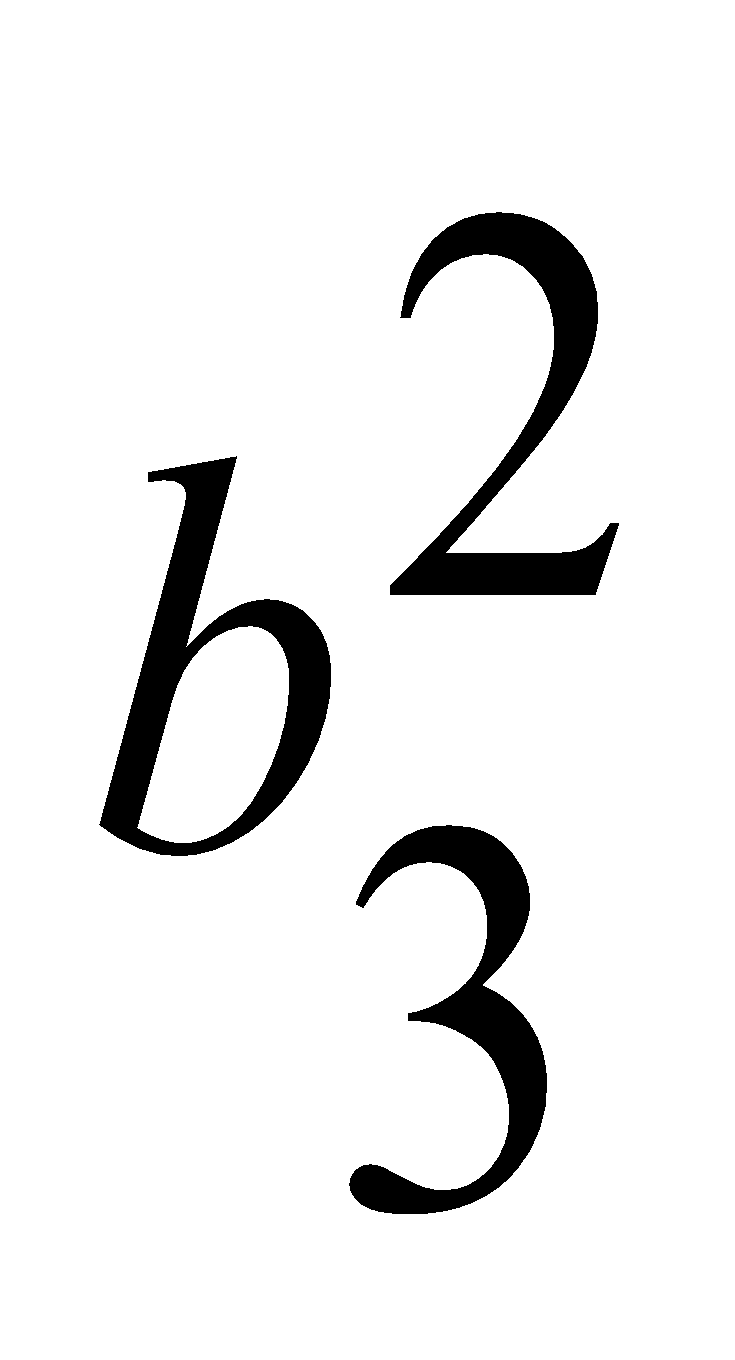 =0.49,
=0.49, 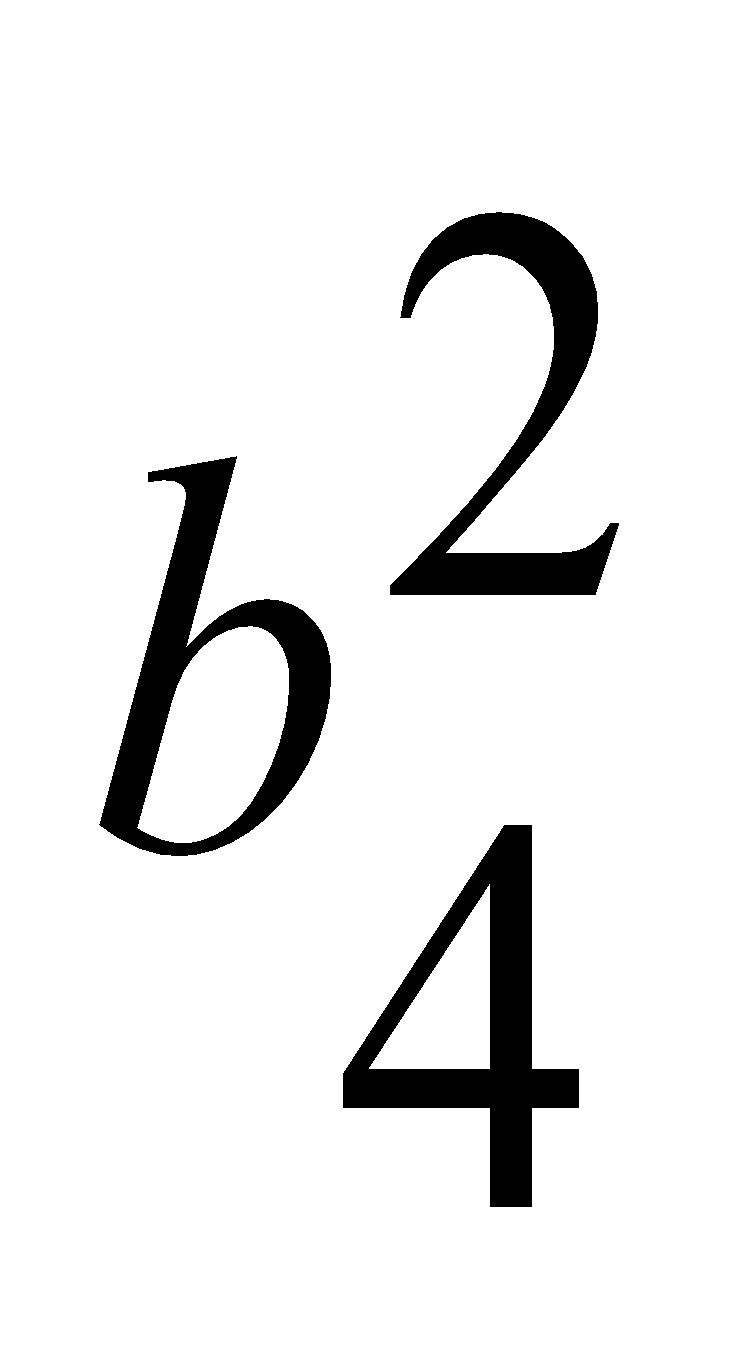
 =0.44. Рейтинговые оценки в рамках этих данных равны 0.462 и 0.619. Таким образом, средняя степень проявления логичности мышления и скорости мыслительных процессов студентов увеличилась за период обучения, что вместе с анализом показателей успеваемости может свидетельствовать о положительной тенденции влияния качества образовательного процесса на развитие общих психофизиологических процессов, навыков и умений студентов.
=0.44. Рейтинговые оценки в рамках этих данных равны 0.462 и 0.619. Таким образом, средняя степень проявления логичности мышления и скорости мыслительных процессов студентов увеличилась за период обучения, что вместе с анализом показателей успеваемости может свидетельствовать о положительной тенденции влияния качества образовательного процесса на развитие общих психофизиологических процессов, навыков и умений студентов.
Список литературы / References
1. Аверкин А.Н., Батыршин И.З., Блишун А.Ф., Силов В.Б., Тарасов В.Б. Нечеткие множества в моделях управления и искусственного интеллекта. — М.: Наука. Гл. ред. физ-мат. лит. — 1986. — 312 с.
2. Olga Poleshchuk and Evgeniy Komarov Expert Fuzzy Information Processing. — Springer-Verlag Berlin Heidelberg. — 2011. — 237 pp.
3. Заде Л.А. Понятие лингвистической переменной и его применение к принятию приблизительных решений. — М., Мир. — 1976. — 165 с.
4. O.Poleshchuk The determination of students’ fuzzy rating points and qualification levels // International Journal of Industrial and Systems Engineering. — 2011. -vol. 9, № 1. — pp. 3-20.
5. Домрачев В.Г., Полещук О.М. Модели оценки эффективности внедрения информационных технологий в образовательный процесс // Информатизация образования и науки. — 2011. — № 2(10). — С.3-13.
6. Полещук О.М. Методы представления экспертной информации в виде совокупности терм-множеств полных ортогональных семантических пространств // Вестник Московского государственного университета леса — Лесной вестник. — 2002. — № 5 (25). С. 198-216.
7. Olga Poleshchuk and Ashraf Darwish Fuzzy Models for Educational Data Mining // Jоuгnal of telecmmunications.— 2012. — vol. 15, № 2, — pp. 8-22.
8. Домрачев В.Г., Комаров Е.Г., Полещук О.М., Санаев В.Г. Комплекс работ по созданию научной базы для разработки образовательных информационных технологий в среде с неопределенными данными// Отраслевая система ЦНИТ: 20 лет на ИТ-рынке России: Cборник статей. — Кемерово, — 2011. — С. 200-204.
