Methods for calculating the second vertical gradient of gravity anomalies
Methods for calculating the second vertical gradient of gravity anomalies
Abstract
Two methods for calculating the second gravity anomaly gradient (SGAG) are discussed. The first method uses the finite-difference scheme of the three-point template, in which the gravity anomalies are arranged along the vertical axis symmetrically with respect to the resultant point. In the second method, a bounded Fourier series expansion on spherical functions is used. The input data are the coefficients of the EIGEN-6C4 geopotential model. The results of determining the SGAG by the differences between the values of gravity anomalies on the physical surface of the Earth calculated at different altitudes and those obtained from the EIGEN-6C4 model are presented. It was found that the maximum discrepancy between the studied methods of obtaining the second anomaly gradient is 65.7178 10-14m-1s-2, which is 0, 4% of the maximum values of the second gradient. Machine time costs are 10 times less in the second method.
1. Введение
В настоящее время очевидными являются успехи в моделировании характеристик ГПЗ различными методами на основе гармонических коэффициентов современных глобальных моделей геопотенциала.
На протяжении нескольких десятилетия гармонический анализ и синтез занимает ведущее место при обработке глобальных данных о гравитационном поле Земли. Он используется для изучения структуры гравитационного поля и его трансформант, выявляет особенности полученных результатов.
Однако остается нерешенной задача определения аномалий силы тяжести, высот квазигеоида и уклонений отвесной линии с высокой точностью, порядка 1 см, 1 мГал и 0,1'' соответственно, на территории Российской Федерации. Исследование современных моделей ГПЗ показало неудовлетворительные по точности и разрешающей способности результаты определения перечисленных характеристик. Особые проблемы вызывает создание помехозащищенных навигационных систем и навигационных гравиметрических карт высокого разрешения , , решение высокоточных задач геодезии, поиск и разведка полезных ископаемых, моделирование остаточных и точечных гравитационных возмущений, таких как горные хребты, границы тектонических плит и особые характерные точки земной поверхности.
Учитывая перечисленные сложности, растущий рост исследований и необходимость повышения точности вычисления характеристик гравитационного поля Земли глобального, регионального и локального масштаба, возобновлен интерес к новым решениям получения характеристик гравитационного поля: первого и второго градиентов потенциала, первого и второго вертикальных градиентов аномалий силы тяжести (ВГАСТ) . Следует заметить, что градиенты аномалии силы тяжести обладают высокой чувствительностью к влиянию небольших и неглубоких аномальных масс. Однако непосредственно из измерений может быть определен только вертикальный градиент силы тяжести, а первый и второй вертикальные градиенты аномалий силы тяжести могут быть найдены путем пересчета аномалий силы тяжести (АСТ) на разные высоты.
В физической геодезии значение второго ВГАСТ используется для вычисления поправочного члена второго порядка теории М. С. Молоденского , . Существует несколько методов вычисления второго градиента АСТ , . Эти методы делятся на конечноразностные, аппроксимационные и условные .
В данной работе сравниваются два метода получения второго градиента. В первом используется конечноразностная схема трехточечного шаблона вычисления АСТ на разные высоты, в котором значения расположены вдоль вертикальной оси симметрично относительно результативной точки. Во втором методе вычисление выполняется с помощью гармонического синтеза по данным модели геопотенциала EIGEN-6C4 .
2. Методы и принципы исследования
В условиях плоской аппроксимации аномалия силы тяжести удовлетворяет уравнению Лапласа
Для определения второго вертикального градиента , согласно уравнению (1), можно использовать следующую формулу
При преобразовании вторых производных Δg к горизонтальной плоскости xyo необходимо перейти от прямоугольных координат к полярным, т. е.
x=r cosA и y=r sinA, где r — радиус-вектор и A — азимут.
Подставляя в формулу (1) выражения (3) и (4) получим
Однако вычисление интеграла в формуле (5) затруднено тем, что при r=0 подынтегральное выражение обращается в бесконечность. В связи с этим формула (5) нуждается в преобразовании.
Наиболее простым и широко применяемым для приближенного вычисления второго ВГАСТ является метод численного дифференцирования уравнения (1) путем применения конечноразностных формул
, .В этом случае производные в формуле (1) заменяются приближенными алгебраическими конечноразностными соотношениями.
Для вычисления второго градиента, используется конечноразностная схема трехточечного шаблона, в котором аномалии силы тяжести Δg расположены вдоль вертикальной оси симметрично относительно результативной точки P(0,0,0) с шагом по высоте h, в интервале [(0,0,-h)<(0,0,0)<(0,0,+h)].
В соответствии с этим шаблоном второй градиент вычисляется как первая производная от первой производной следующим образом:
Окончательная расчетная формула примет вид
Для вычисления Δg, расположенных вдоль вертикальной оси в точкахP(0,0,-h), P(0,0,0) и P(0,0,+h), использовано разложение в ряд:
где fM — геоцентрическая гравитационная постоянная;
N — предельная степень разложения;
ae — экваториальный радиус Земли;
r=R+H — радиус-вектор точки P(0,0,0) на земной поверхности с координатами φ и λ (геоцентрическая широта и долгота точки);
R — средний радиус Земли;
H — высота точки ;
— разность коэффициентов сферических функций реального и нормального поля силы тяжести;
и
— гармонические коэффициенты нормального геопотенциала, при этом
. Гармонические коэффициенты геопотенциала отнесены к эллипсоиду WGS-84 и являются нормированными.
Вычисления Δg по формуле (8) определяются в сферической системе координат (φ,λ,r), поэтомуи в конечноразностной схеме трехточечного шаблона использована та же система координат. Тогда формулу (7) для вычисления второго градиента методом численного дифференцирования представим в следующем виде
где Δr — изменение r, которое соответствует шагу по высоте h в схеме трехточечного шаблона в прямоугольной системе координат (7).
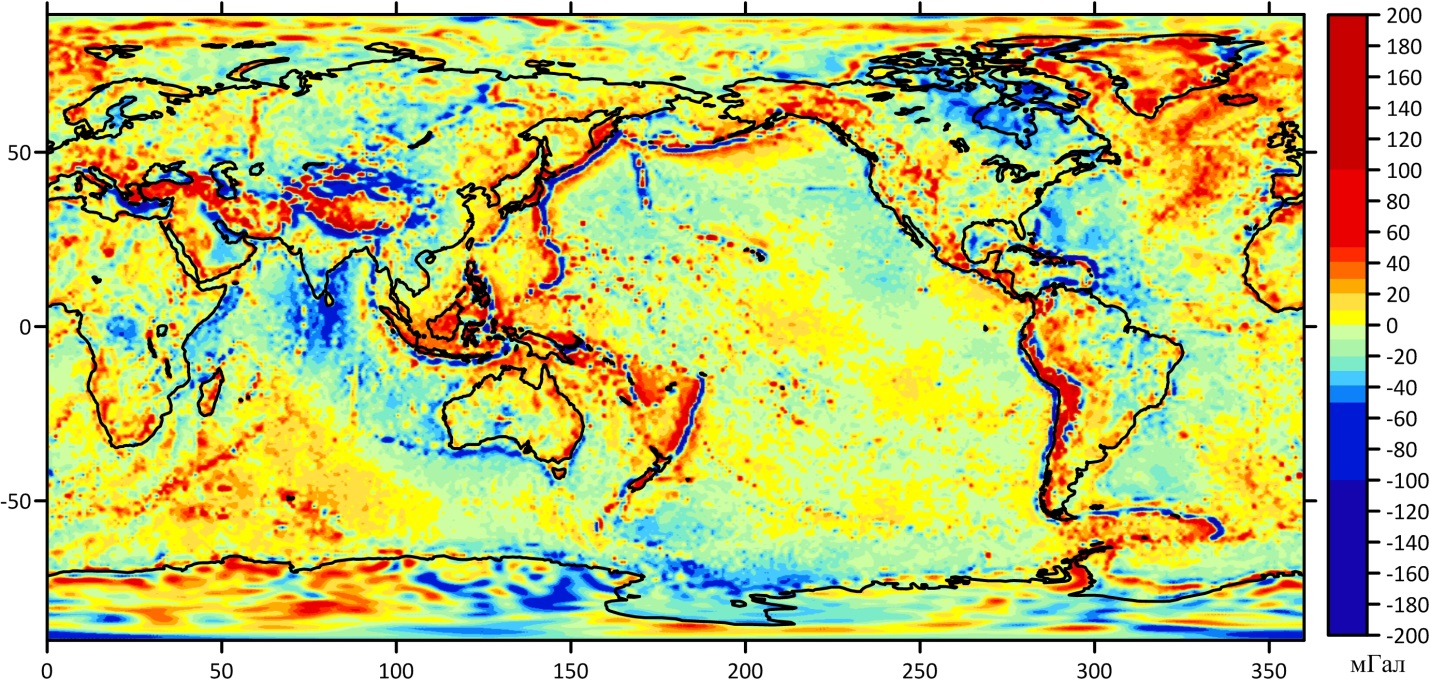
Рисунок 1 - Глобальные Δg, вычисленные по формуле (8) при Δr=0
Визуализация результатов вычисления ВГАСТ, полученных по формуле (9), в которой использованы значения: Δg(φ,λ,r-Δr) при Δr=-1 м, Δg(φ,λ,r) при Δr=0 и Δg(φ,λ,r+Δr) при Δr=+1 м, вычисленные по формуле (8), показана на рисунке 2.
Изменения значений находятся в диапазоне от -1,121 ⋅ 10-9 м-1с-2 до +0,156 ⋅ 10-9 м-1с-2.
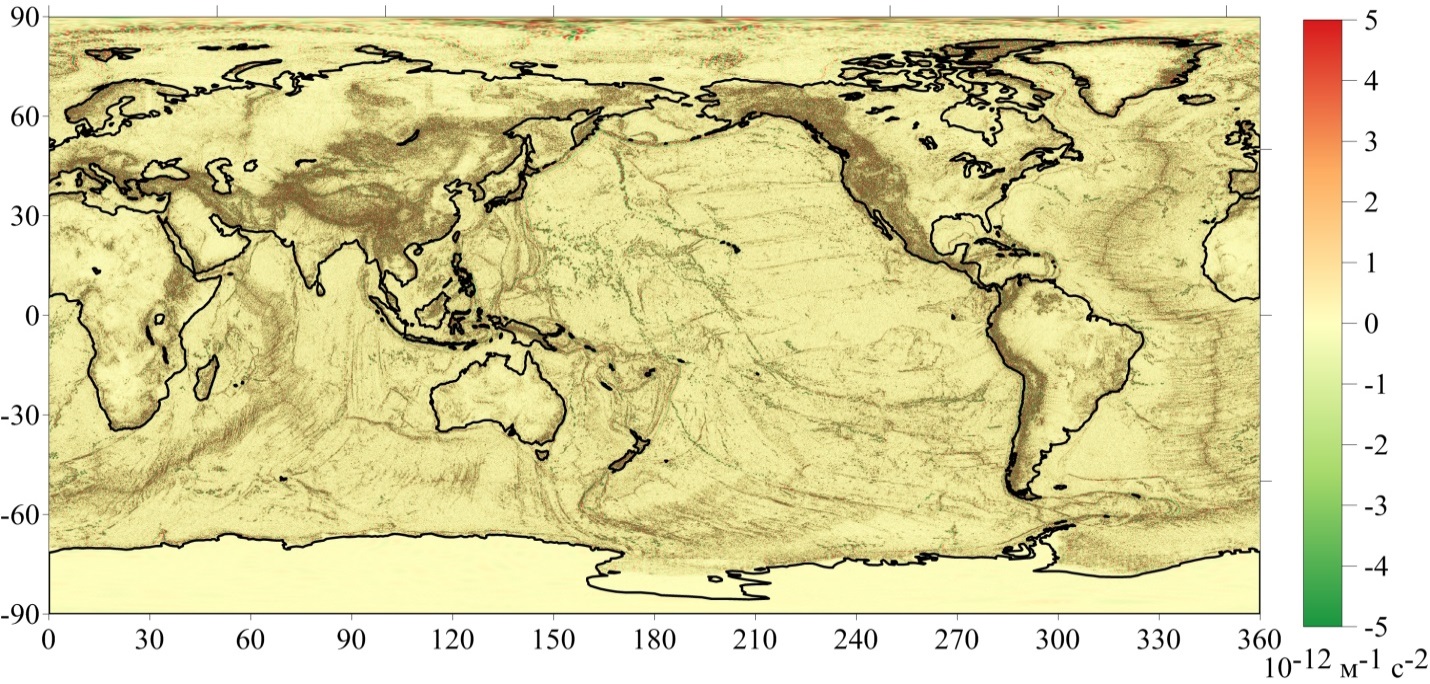
Рисунок 2 - Визуализация результатов, полученных по формуле (9)
Примечание: изменения значений (∂2Δg(P))/(∂r2) ограничены диапазоном от -0,5 ⋅ 10-12 м-1с-2 до +5,0 ⋅ 10-12 м-1с-2
В горных областях земной поверхности значения весьма значительны (рисунок 3).
Далее рассмотрен метод определения второго градиента АСТ с помощью разложения в ограниченный ряд по сферическим функциям, в котором использованы коэффициенты модели геопотенциала EIGEN-6C4 до степени N=2190 .
Так как второй вертикальный градиент АСТ является третьим градиентом от аномального потенциала, то:
где T(P) — аномальный потенциал (разность между реальным и нормальным потенциалами Земли).
Изменения третьего градиента от аномального потенциала находятся в диапазоне от -1,121 ⋅ 10-9 м-1с-2 до +0,156 ⋅ 10-9 м-1с-2.
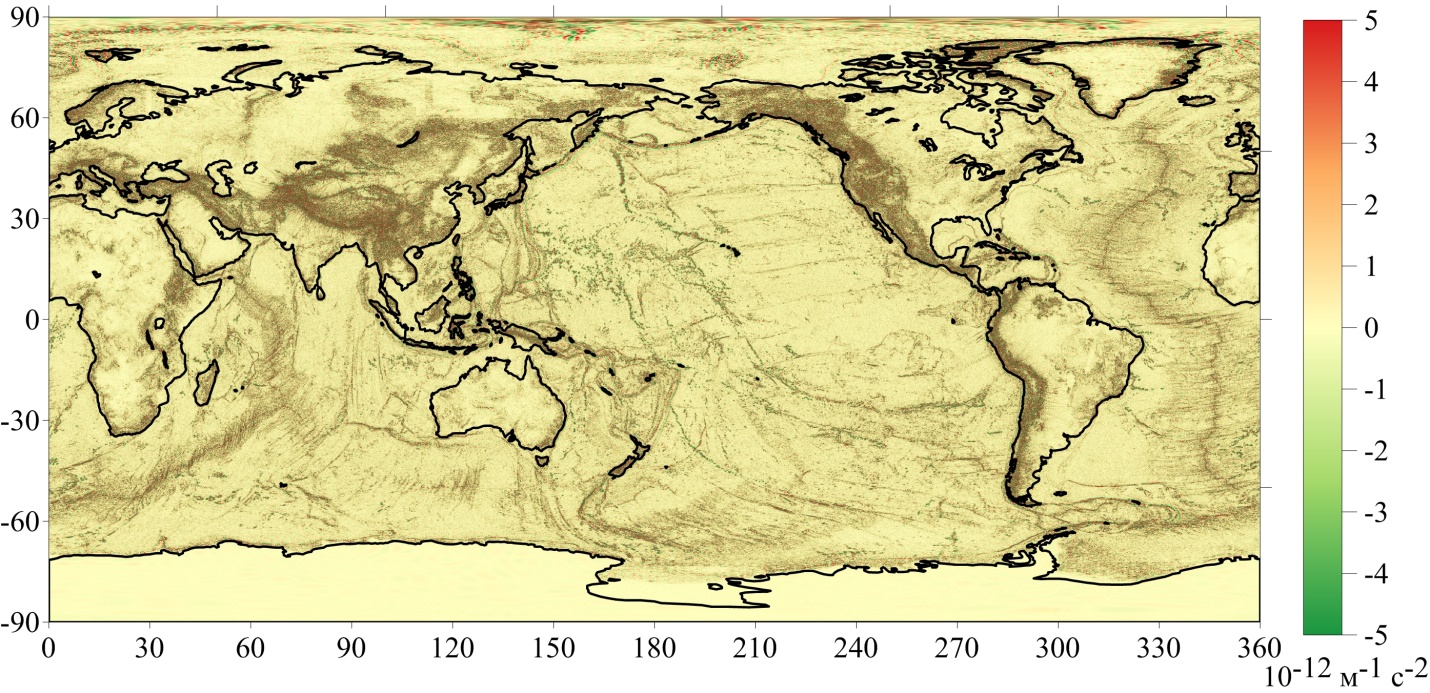
Рисунок 3 - Визуализация результатов вычисления (∂3T(P))/(∂r3), полученных по формуле (10)
Примечание: изменения (∂3T(P))/(∂r3) ограничены диапазоном от -0,5 ⋅ 10-12 м-1с-2 до +5,0 ⋅ 10-12 м-1с-2
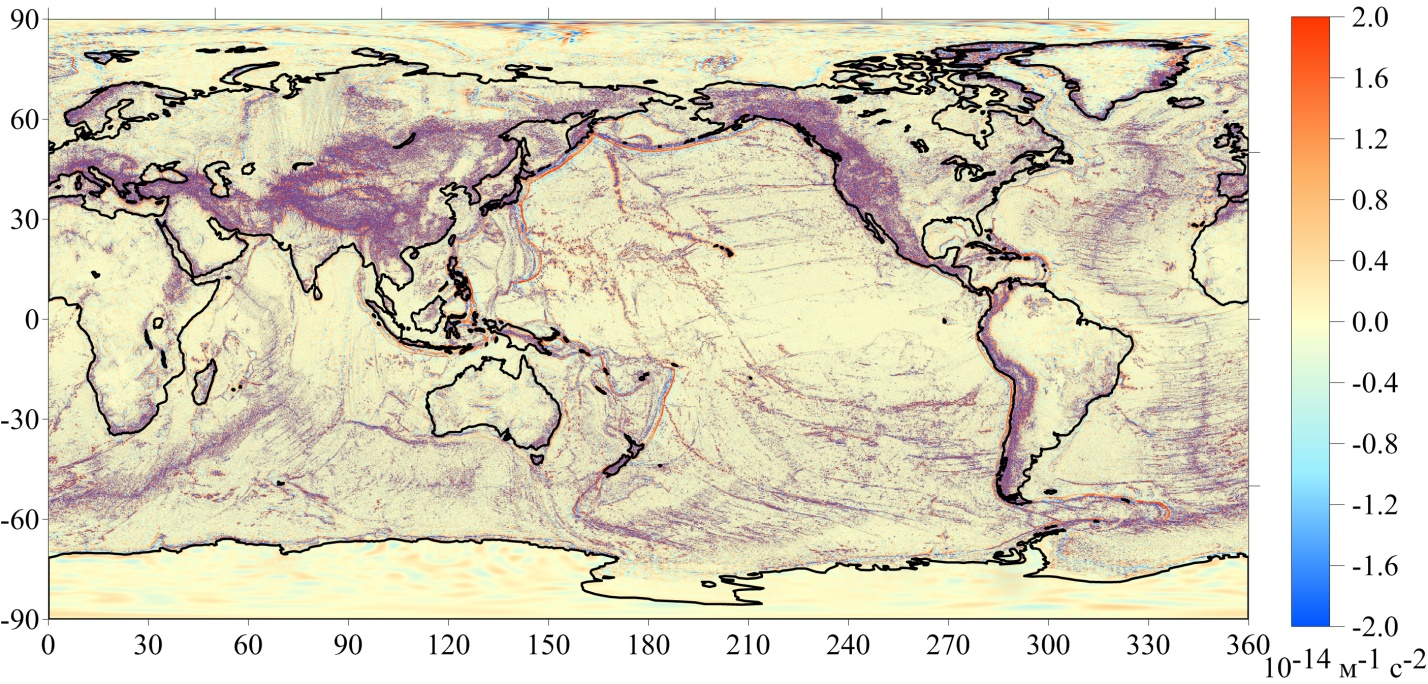
Рисунок 4 - Распределение разности ΔG между вторыми вертикальными градиентами, полученными по формулам (9) и (10)
Гистограмма распределения значений (рисунок 5) по характеру соответствует почти нормальному закону: 79% значений находится в диапазоне от -1,0 ⋅ 10-14 м-1с-2 до +1 ⋅ 10-14 м-1с-2.
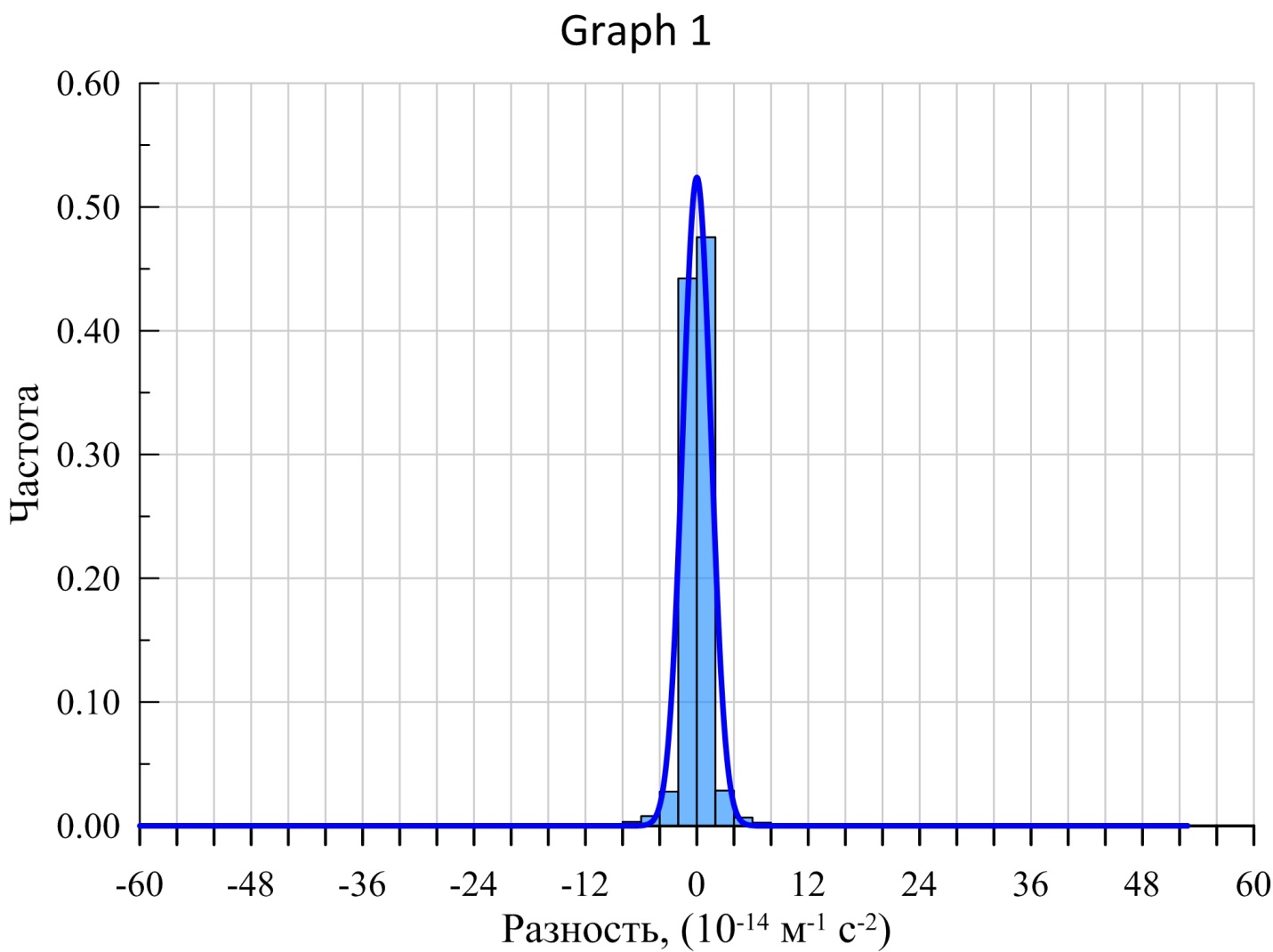
Рисунок 5 - Гистограмма распределения значений ΔG
3. Заключение
Для решения фундаментальных и прикладных задач, связанных с определением высокоточных характеристик гравитационного поля, получен второй вертикальный градиент АСТ.
Сравнение результата конечноразностной схемы трехточечного шаблона, в котором расположены вдоль вертикальной оси оz симметрично относительно результативной точки, с результатами гармонического синтеза показало расхождение в 0,4% от максимальных значений второго градиента по аномалии.
Определение данной характеристики гравитационного поля возможно любым из рассмотренных методов. Применение гармонического анализа приводят к уменьшению затрат машинного времени в 10 раз.