SYMMETRIES AND EXACT SOLUTIONS OF A MULTIPLICATIVE CLASS OF DIFFERENTIAL EQUATIONS WITH EXPONENTIAL FUNCTIONS
SYMMETRIES AND EXACT SOLUTIONS OF A MULTIPLICATIVE CLASS OF DIFFERENTIAL EQUATIONS WITH EXPONENTIAL FUNCTIONS
Abstract
This article studies discrete symmetries of a class of 2nd order ordinary differential equations with multiplicative right values.
Discrete transformations closed in the studied class of equations are found. The discrete group of transformations and its graph are constructed. All elements of the orbit of the original multiplicative equation containing the exponential function are obtained.
The method of finding exact solutions of the equations of the specified orbit at some values of the parameters included in the equations is presented. Examples of finding solutions to the equations of this orbit are discussed.
In this work, the method of extending the class of equations, as well as the method of "multiplication" of solvable cases in the studied class of equations, based on the fact that solutions of equations are related by the same transformations as the equations themselves, are used.
1. Введение
Дискретно-групповой анализ обыкновенных дифференциальных уравнений (ДГА ОДУ) был разработан В. Ф. Зайцевым в конце 20-го века. Он открыл дискретные группы преобразований дифференциальных уравнений.
Основой ДГА ОДУ является поиск преобразований, замкнутых в исследуемом классе уравнений. (До В. Ф. Зайцева были известны лишь простейшие из таких преобразований, например ,
и т.д.) Важным приложением ДГА ОДУ является алгоритмизированный поиск их точных решений.
Первая наиболее полная работа, в которой изложены основы ДГА ОДУ и приведены точные решения сотен новых разрешимых уравнений, полученных В. Ф. Зайцевым, его коллегой А. Д. Поляниным и их научными школами – это справочник-монография (в эту же книгу вошли, в частности, основные теоретические и практические результаты кандидатской диссертации автора данной статьи).
В последующих справочниках-монографиях этих же авторов содержатся точные решения уже тысяч новых интегрируемых уравнений, найденных методом «размножения» по дискретным группам (см. далее).
К сожалению, в настоящее время дискретным группам преобразований ОДУ математическим сообществом уделяется незаслуженно мало внимания: считанное число математиков занимается исследованием ОДУ с помощью дискретных групп преобразований. Большинство «групповиков» занимаются непрерывными группами преобразований, причём в основном, для уравнений с частными производными.
Данной статьёй, так же как и прошлыми работами
, и т.д., автор пытается ликвидировать этот пробел в теории дифференциальных уравнений.В данной работе рассматриваются дискретные симметрии мультипликативного класса обыкновенных дифференциальных уравнений (ОДУ) 2-го порядка:
Исследование симметрий этого класса уравнений было начато В. Ф. Зайцевым с подкласса (1) при
причём, со случая степенных функций K, L, M:
(класс уравнений (3) называется классом обобщённых уравнений Эмдена-Фаулера).
В работах
, , , , класс степенных уравнений (3) был расширен:– для достижения замкнутости некоторых дискретных преобразований.
В статьях
, , было начато исследование дискретных симметрий класса уравнений (1) с произвольными функциями, а также были рассмотрены некоторые спецификации, в частности, уравнение свободных колебаний маятника. В данной статье исследуется ещё одна спецификация: уравнения классов (1) и (2) содержат экспоненциальные функции.Наличие дискретной группы преобразований, замкнутых в рассматриваемом классе уравнений, позволяет находить новые разрешимые случаи в этом классе уравнений с помощью метода «размножения» по данной дискретной группе: если известно решение, частное или общее, хотя бы одного уравнения, соответствующего некоторой вершине графа группы, то с помощью преобразований данной дискретной группы можно получить решения всех остальных уравнений, соответствующих остальным вершинам графа.
В статье используются, в частности, следующие термины: дискретная группа преобразований, порождающий (образующий) элемент и определяющие соотношения дискретной группы, код дискретной группы, группа диэдра и т.д., с определениями которых можно ознакомиться в работах
, .2. Применение группы к классу уравнений с экспонентой
Для класса уравнений (1) с произвольными функциями была построена
, , группа диэдра D6 12-го порядка – группа преобразований, замкнутых в (1):(E – тождественное преобразование), где r и h – образующие группы (5);
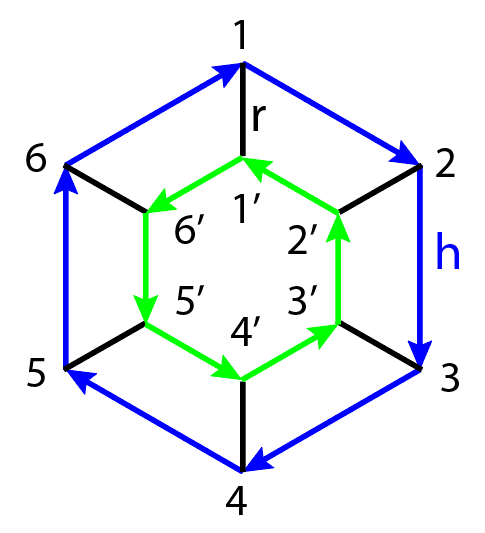
Рисунок 1 - Граф группы D6
Таблица 1 - Уравнения-вершины графа на рис. 1
Примечание: вершина 1 соответствует (8)
3. Применение группы D3 к (8)
Для класса уравнений (2) была построена , группа диэдра D3 преобразований, замкнутых в (2):
где r и g – образующие дискретной группы D3;
(показатель «-1» в (11) означает обратную функцию).
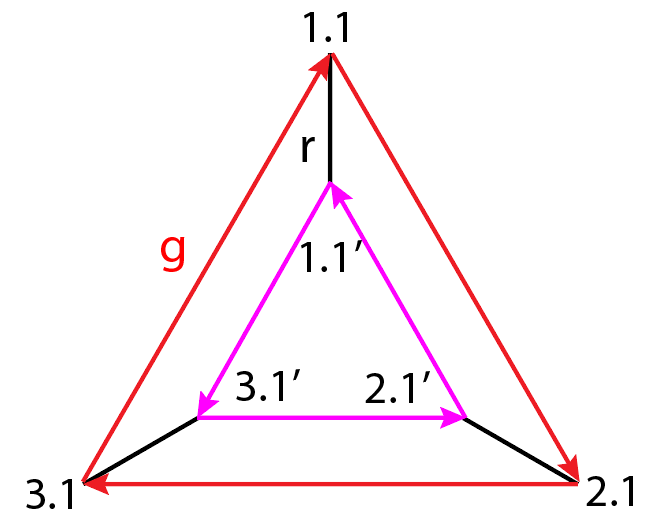
Рисунок 2 - Граф группы D3
Таблица 2 - Уравнения-вершины графа на рис. 2
Примечание: вершина 1.1 обозначает (12)
Преобразование g зависит от функций K, L, M преобразуемого уравнения, поэтому при каждом следующем применении уравнение g имеет другой вид.
С помощью (11) можно вычислить преобразование g на каждом шаге:
Так как преобразования g и r замкнуты в классе уравнений (2), то все уравнения таблицы 2 имеют вид (2).
Удивительным фактом является то обстоятельство, что только уравнения 1.1 и 1.1’ содержат экспоненты. Остальные 4 уравнения являются степенными. Уравнения 1.1 и 1.1’ являются сингулярными элементами степенного класса уравнений (3), соответствующими в (3) случаям k=∞ и l=∞ для 1.1’.
4. Применение дискретной группы 36-го порядка к (12)
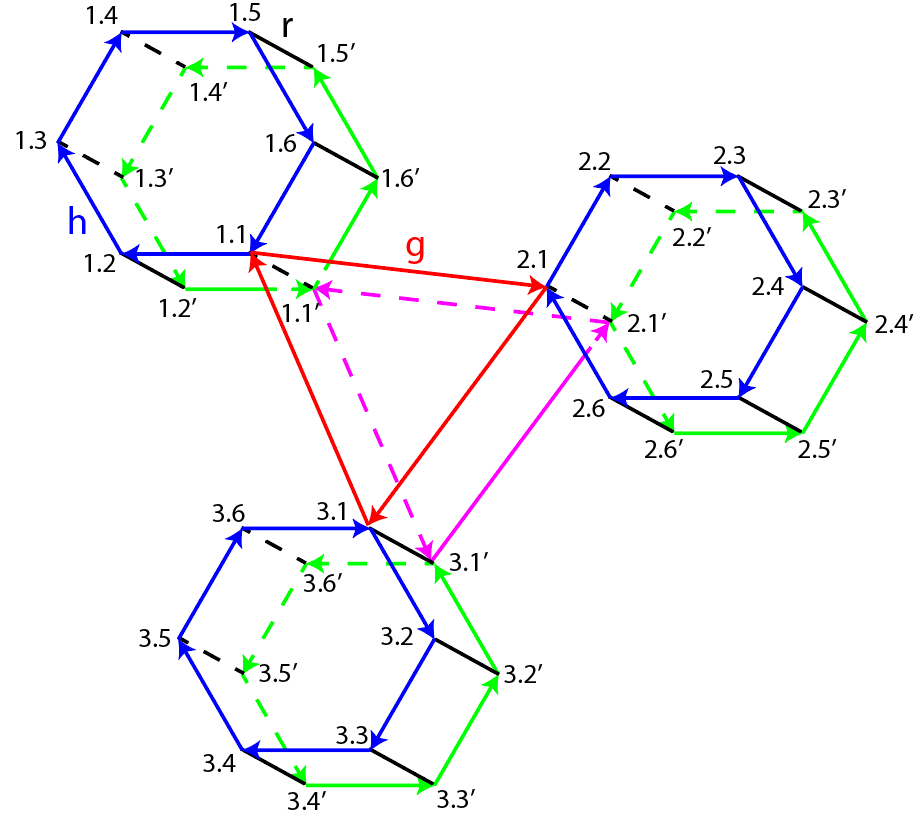
Рисунок 3 - Граф группы 36-го порядка
Таблица 3 - Уравнения-вершины графа на рис. 3
Примечание: вершина 1.1 обозначает (12)
5. Нахождение точных решений уравнений орбиты (12)
Если одно из уравнений таблиц 1, 2, 3 при некоторых значениях параметров является интегрируемым, то это же можно сказать обо всех остальных уравнениях в этих таблицах. Метод «размножения» разрешимых случаев в рассматриваемых классах уравнений основан на том, что преобразования дискретных групп (здесь 6-го, 12-го и 36-го порядков), связывающие уравнения, связывают и их решения. Кроме того, если решение исходного уравнения выражается через некоторые элементарные или специальные функции, то и решения уравнений его орбиты (здесь остальных уравнений таблиц 1, 2, 3) выражаются через эти же функции. Указанные выше преобразования легко установить по графам на рис. 1, 2, 3 – они являются композициями образующих g, h, r.
С помощью метода «размножения» известный справочник Камке по ОДУ был значительно расширен: единичные разрешимые случаи различных классов уравнений были «размножены» до десятков и сотен
, , , .Пример 1. Рассмотрим уравнение (12) при ,
:
оно имеет номер 1.1 на рис. 1 и в таблице 1.
Его общее решение в параметрическом виде
:Найдём, к примеру, решение уравнения 1.3’:
Согласно рис. 3, уравнение 1.3’ (15) приводится к уравнению 1.1 (13) преобразованием h2r; с помощью (6) и (7) его легко вычислить:
Композиция (16) и (14) является общим решением уравнения 1.3’ (15):
.
Пример 2. Аналогично вычислим решение, например, уравнения 1.2’:
Это немного сложнее, так как уравнение 1.2’ (17) приводится к уравнению 1.1 (13) не с помощью точечного преобразования, а с помощью касательного преобразования:
Заметим, что преобразование hr оказалось известным касательным преобразованием Лежандра, в котором x и y зависят от производной. Дополнительно необходимо в решении (14) уравнения 1.1 (13) вычислить и
:
Таким образом, композиция преобразования hr (18) и общего решения (14, 19) уравнения 1.1 (13) является общим решением уравнения 1.2’ (17):
Замечание. С помощью операции масштабирования можно вычислить решения всех уравнений орбиты исходного уравнения (13) с произвольными коэффициентами в правых частях.
6. Заключение
Обыкновенные дифференциальные уравнения нередко возникают в различных разделах естествознания, особенно при решении уравнений математической физики и механики
, .В данной статье дискретные группы преобразований 6-го, 12-го и 36-го порядков применены к мультипликативному классу ОДУ 2-го порядка, содержащему в правой части степенные и экспоненциальный сомножители.
Найдена орбита исходного дифференциального уравнения, состоящая из 36-ти мультипликативных уравнений, содержащих в правых частях экспоненциальные функции. Приведён метод «размножения» разрешимых случаев исходного дифференциального уравнения: если при некоторых параметрах исходное уравнение интегрируется, то интегрируются также все уравнения его орбиты, причём их решения выражаются через те же функции, что и решение исходного уравнения.
Рассмотрены примеры, иллюстрирующие получение точных решений уравнений, содержащих экспоненциальные функции, через решение исходного дифференциального уравнения.
В дальнейшем можно в (12) рассмотреть ekx вместо ex, а также расширить дискретную группу 36-го порядка для интегрируемых подклассов класса уравнений (12).
