CRITICAL DISCHARGE OF POWDER-GAS MIXTURE FROM THE NOZZLE OF POWDERED FUEL SUPPLY SYSTEM
CRITICAL DISCHARGE OF POWDER-GAS MIXTURE FROM THE NOZZLE OF POWDERED FUEL SUPPLY SYSTEM
Abstract
In the present work, nonequilibrium critical isothermal discharge of powder-gas medium from a conical channel is studied. Such a discharge is implemented in the supply system of promising power units using powdery components as fuel. A one-dimensional mathematical model, supplemented with new assumptions, equations, and physical constraints, is formed on the basis of earlier works. The calculation of the flow of aluminium powder ASD-1 in the assumed pressure range (0.5...4 MPa) of the feed system operation of prospective power units is presented. Comparison of the results of numerical modelling and experimental data shows coincidence at qualitative and quantitative level.
1. Введение
В настоящее время ведется изучение вопросов, связанных с созданием новых перспективных энергоустановок на порошкообразных и гранулированных топливах , , , . Один из таких комплексных вопросов – организация эффективной подачи топлива в камеру сгорания (КС). Для создания принципиально новой системы подачи с теоретической точки зрения необходимо проводить математическое моделирование, получить параметры процесса истечения порошкообразного топлива.
Подача порошкообразного топлива осуществляется в среде несущего инертного газа – рассматривается истечение «порошково-газовой» среды. Для создания высокоэффективных и безопасных энергоустановок система подачи требует критический режим истечения, при котором процессы, происходящие в КС, не влияют на процессы протекающие в системе подачи , , , . Ключевой параметр такого истечения – критическое отношение давлений (), характеризующее отношение давления в критическом сечении к давлению перед форсункой (в начале канала) , , :
где – давление в критическом сечении;
– давление на входе в конический канал.
Из газовой динамики известно, что для газов в зависимости от давления. Однако для порошково-газовой среды
имеет нелинейный характер, который не объясняется газовой динамикой. Расходы фаз также имеют нелинейный характер. Несмотря на то, что в работе приведены уравнения, которые используются для описания процесса, в настоящее время полная математическая модель не сформирована, для неё не записаны физические ограничения, граничные условия.
Из работ , , известно, что истечение высококонцентрированной порошково-газовой смеси в коническом канале может происходить в несколько этапов: уплотнение, движение в плотном слое, переходный режим, режим истечения в псевдоожиженном слое. В процессе упаковки порошка, при увеличении напряжения в дисперсной фазе порозность (объем газа в рассматриваемом объеме,
) сыпучего материала уменьшается вплоть до предельного значения
. При дальнейшем увеличении напряжений, порозность материала остается постоянной, т.е. возникает режим предельно уплотненного слоя. При уменьшении напряжения сыпучей среды
происходит разуплотнение (увеличение порозности), вплоть до полного разряжения потока (
). Таким образом, условие начала разуплотнения:
. Стоит отметить, что
– величина, отражающая свойства рассматриваемого зернистого материала. Для каждого порошка она имеет свое значение, которое зависит от физико-механических свойств. Для порошка со сферическими частицами одинакового размера
(такой порошок можно назвать «идеальным»).
2. Методы и принципы исследования
Использованы методы и подходы теории газовой динамики двухфазных сред, математического моделирования процессов фильтрации газа в зернистой среде и ее движения в плотном и псевдоожиженном слоях, а также проведения экспериментальных исследований процессов течения двухфазных потоков.
Цель настоящего исследования – проведение математического моделирования критического неравновесного истечения порошково-газовой среды из отверстия. В первом приближении проводится одномерное моделирование истечения порошково-газовой среды из конической форсунки, которое позволяет рассчитать параметры системы подачи.
Решаемые задачи
1. Сформировать математическую модель критического неравновесного истечения порошково-газовой среды из форсунки.
2. Определить закономерности критического истечения порошково-газовой среды.
3. Провести анализ полученных результатов.
Допущения, принимаемые в математической модели
1. Рассматривается задача одномерного течения порошково-газовой смеси.
2. Влияние гравитационных сил не учитывается (их воздействие на поток пренебрежимо мало).
3. В рассматриваемом объеме массовая доля газовой фазы на два-три порядка меньше, чем доля дисперсной фазы (от 0,1 до 2%).
4. Поток порошково-газовой среды изотермичен (). В рассматриваемом объеме масса газа много меньше, чем масса частиц, а в связи с большой удельной поверхностью частиц, между газом и порошком происходит интенсивный теплообмен
5. Рассматриваемый газ – идеальный (подчиняется уравнению Клапейрона-Менделеева).
6. Потери давления на трение при движении в режиме предельно уплотненного слоя учитываются (через значения , определенные экспериментально), в режиме псевдоожиженного слоя не учитываются (в этом случае величина сил трения незначительна, ими можно пренебречь).
7. В режиме уплотненного слоя предполагается, что поток движется как пористое тело в напряженно-деформированном состоянии (в текущем поперечном сечении скорости частиц равны). В режиме разуплотненного потока порошок ведет себя как жидкость («псевдожидкость»), соответственно, возникает пограничный слой. Скорости частиц порошка у стенки и в ядре потока неравны, удельный расход через сечение уменьшается. В теории жидкости это эффективно учитывается через уменьшение площади поперечного сечения – вводится «толщина вытеснения» (). В данной модели применяется тот же подход. Толщина вытеснения определяется через сопоставление рассчитанного удельного расхода порошка и экспериментально измеренного для одной точки соответствующей определенному давлению. Для других значений давления расчеты проводятся с учетом ранее полученной толщины вытеснения.
8. Порошок – сыпучий, несвязный материал (требование для порошкообразного топлива, применяемого в энергоустановках
). Кроме этого, рассматриваемый порошок – близок к идеальному.9. В начальном сечении порозность принимается равной предельному значению для данного порошка (т.е. течение в рассматриваемом объеме начинается в режиме предельно уплотненного слоя). Далее по потоку порозность может быть больше чем
, но не меньше.
10. Разуплотнение происходит «скачком». Разуплотнение – процесс вероятностный. Любая флуктуация способна приводить поток в разуплотненное состояние (грубая шероховатость, выступы в канале). Условие начала разуплотнения: модуль равнодействующей аэродинамической силы () больше модуля реактивной силы (
) [8]. Условие существования движения разуплотненной среды в режиме псевдоожиженного слоя – равенство модулей
и
, действующих на элементарный объем порошково-газовой среды. Равнодействующая сила
– градиент давления вдоль канала. Равнодействующая сила
– сумма силы реакции стенки и силы инерции. Одно из решений приведенной системы
, т.е. разуплотнение не происходит до конца конического канала. Для того чтобы рассмотреть другие решения, необходимо ввести разуплотнение искусственно, задав координату и порозность разуплотнения.
Математическая модель
Рассмотрим систему уравнений, сформированную на основании законов сохранения импульса и расходов фаз
, . Уравнение (1) (уравнение сохранения импульса) отражает зависимость изменения скорости порошка от изменения давления газа . Интегрируется в случае разуплотненного режима истечения.где – удельный расход газа, кг/(с⋅м2);
– скорость порошка, м/с.
Уравнение (2) отражает зависимость изменения давления газа от порозности среды, объемной поверхности частиц порошка и удельной силы газового потока вдоль оси канала (градиент давления)
.где – порозность порошка;
– объемная поверхность порошка, м-1;
– удельная сила газового потока
Уравнения (3) и (4) – уравнения неразрывности для газа и порошка соответственно, в которых учтена порозность среды:
где – скорость газа, м/с;
– площадь сечения, м2;
– плотность частиц порошка, кг/м3;
– плотность газа, кг/м3;
Уравнение (5) – формула для вычисления неравновесной изотремической критической скорости порошка. Впервые выведена в работе
:(6) – Уравнение Козени для «идеального» порошка:
где – средний диаметр частицы порошка, м;
Кроме того, в дальнейшем, для моделирования пневмотранспорта реальных зернистых сред возможно использовать существующие подходы, позволяющие учитывать их мультидисперность и реальную форму
.где – коэффициент извилистости
Уравнение состояния идеального газа:
Уравнение (11) – критерий Рейнольдса, определяет характер течения в текущем сечении: для двухфазных систем ламинарный режим течения наблюдается при значении числа Рейнольдса порядка 1, свыше - турбулентный.
где – динамическая вязкость газа, Па∙с.
Для определения точки перехода истечения от плотного слоя к разуплотненному (), воспользуемся условием, полученным в
где – угол образованный стенкой конического участка с осью, вдоль которой движется поток;
– текущие значение радиуса. Если расчет предполагает достижения разуплотнения, то поскольку разуплотнение происходит скачком, вводятся следующие величины:
– координата начала разуплотнения, м;
– порозность в момент разуплотнения.
В выражении (12) первое слагаемое представляет собой модуль , второе – модуль
. При достижении координаты разуплотнения, выполняется проверка по выражению (12). Если
,
заданы верно, условие (12) будет выполняться (с заданной точностью). В режиме разуплотненного потока выполняется другое условие, свидетельствующие о том, что поток движется в режиме псевдожидкости, выводимое из уравнения (1):
или .
Варьируемые параметры и граничные условия
Параметры, которые варьируются для достижения сходимости решения: критическое отношение давлений (), отношение расходов газа и порошка (
), критическая порозность (
). Сложность моделирования – варьируемые параметры связаны с граничными условиями, которые выводятся из уравнений (3)-(5).
Физические ограничения
1. В рассматриваемом коническом канале максимальная скорость должна достигаться на выходе и быть равной (с заданной точностью), рассчитанной по уравнению (5) (
).
2. Порозность в текущем сечении не может быть меньше, чем для рассматриваемого порошка (по допущению 9,
). Если в зоне разуплотнения порозность опускается до своего минимального значения, то расчет принимается некорректным, так как в таком случае нельзя использовать уравнение (1).
3. В виду того, что в режиме разуплотненного потока потери давления на трение не учитываются и для того, чтобы получить единственное значение , выведем уравнение сохранения энергии из уравнения (1) с учетом наличия параметров разуплотнения:
где – приведенная скорость (отношение скоростей порошка в зоне разуплотнения и в критическом сечении). Кроме того, выражение (14) будет соблюдаться только тогда, когда верно заданы параметры разуплотнения.
Система уравнений (1)-(14) описывает одномерное истечение двухфазной (порошково-газовой) среды в конической форсунке как в случае течения в режиме уплотненного слоя, так и в режиме псевдоожиженного слоя.
Исходные данные для расчета
В качестве физических исходных данных задается (таблица 1) геометрия канала, параметры порошкового материала, параметры несущего газа. Сходимость достигается путем варьирования параметров (). Для первичной верификации модели, задаются параметры порошка алюминия АСД-1, так как имеются экспериментальные данные по его критическому истечению . Предельная порозность
принята 0,34 (АСД-1ПСК) .
Таблица 1 - Исходные данные расчета
Параметр | Значение |
Радиус критики, мм | 1,25 |
Длина участка, мм | 20 |
Угол, ° | 45 |
Средний диаметр частиц, мкм | 20 |
Плотность материала, кг/м3 | 2700 |
Температура газа, К | 298,15 |
Газовая постоянная, Дж/(кг∙К) | 296,5 |
Динамическая вязкость, Па∙с | 17,78∙106 |
3. Основные результаты
На рис. 1 представлены рассчитанные характерные параметры процесса истечения при заданном давлении на входе ( МПа): отношение модулей равнодействующих сил
и
, действующих на элементарный объем и коэффициент порозности
. Из рисунка следует, что условие начала разуплотнения (12) и условие существования течения разуплотненного потока в режиме псевдожидкости выполняется, а порозность после разуплотнения изменяется, но при этом не достигает своего минимального значения, что указывает на разуплотненное течение, вплоть до критического сечения.
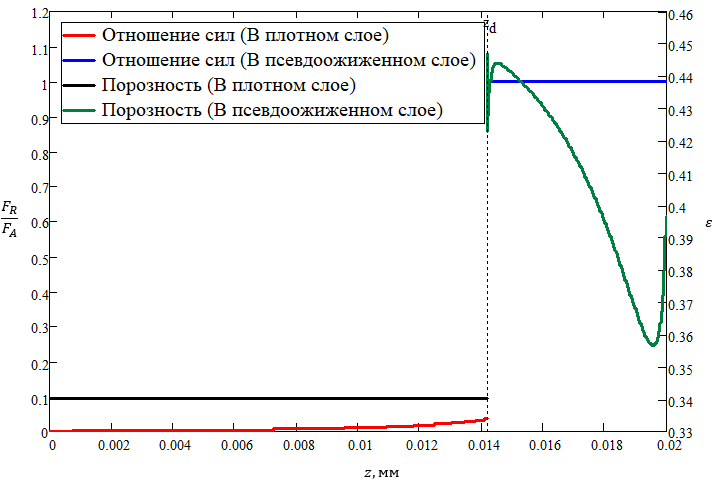
Рисунок 1 - Отношение равнодействующих сил, действующих на элементарный объем, коэффициент порозности
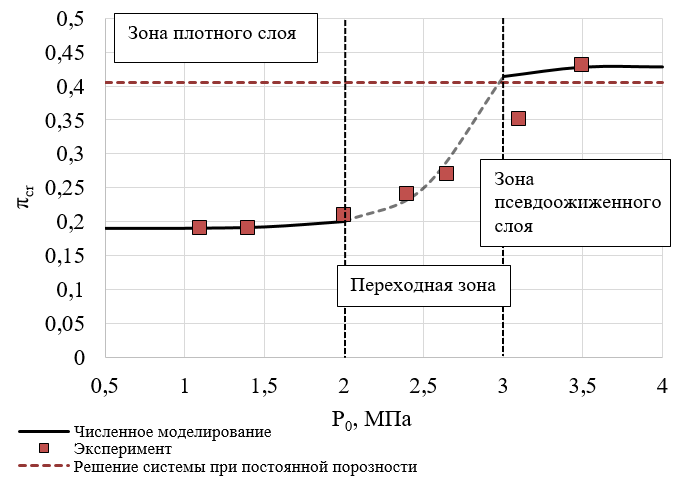
Рисунок 2 - Зависимость критического отношения давлений от давления на входе, сравнение численного моделирования и эксперимента
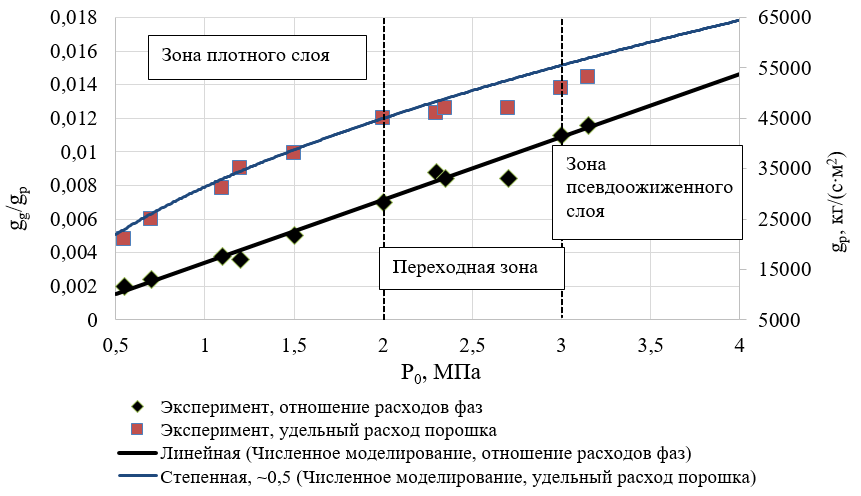
Рисунок 3 - Зависимости отношения удельных расходов фаз, удельного расхода порошка от давления на входе, сравнение численного моделирования и эксперимента
4. Обсуждение
Достоверность и обоснованность результатов и выводов работы обеспечивается: использованием основополагающих уравнений механики сплошных сред, опробованных методик, хорошим согласованием результатов расчёта и экспериментальных данных других авторов.
Из рисунка 2 следует, что моделирование переходной зоны затруднено, так как недостаточно сведений о физике переходного процесса. Тем не менее промоделированные точки в зонах плотного слоя и псевдоожиженного слоя численно согласуются с результатами эксперимента. Из рисунка 2 также следует, что при низких давлениях (до МПа) поток по каналу движется в режиме плотного слоя, а с давления
МПа поток разуплотняется, движется в режиме псевдоожиженного слоя.
Качественное и численное совпадение достигается для зависимости отношения удельных расходов газа и порошка от давления на входе в форсунку (рис. 3) – в экспериментальном и расчетном случае эта величина изменяется линейно на рассматриваемом диапазоне давлений. Качественное и численное совпадение достигается и для зависимости расхода порошка от давления на входе (рис. 3) – в обоих случаях она пропорциональна в степени 0,5.
5. Заключение
1. Усовершенствована математическая модель неравновесного изотермического критического истечения высококонцентрированной порошково-газовой среды из отверстия. Сформулированы допущения в модели, записаны уравнения, определены физические ограничения.
2. Рассмотрен предполагаемый диапазон давления работы системы подачи перспективной энергоустановки (0,5…4 МПа). Достигнуто качественное и численное совпадение экспериментальных данных и результатов численного моделирования для установившихся режимов – движение плотного слоя и псевдоожиженного слоя. Зависимости от давления на входе форсунку: отношение удельных расходов фаз – линейная, удельный расход порошка – корневая.
Разработанная математическая модель обеспечивает моделирование процессов истечения порошково-газовой среды из конических форсунок и позволяет рассчитать параметры системы подачи перспективной энергоустановки, применяющей порошкообразное топливо.
