Modelling of natural convection in a two-dimensional U-shaped channel with vertical temperature gradient
Modelling of natural convection in a two-dimensional U-shaped channel with vertical temperature gradient
Abstract
The work examines the solution of the problem of calculating the temperature and velocity field of water in a two-dimensional curved U-shaped channel heated from below, modelling a U-shaped tube. The calculation is based on the solution of the system of Navier-Stokes, heat conduction and continuity equations in the Boussinesq approximation by the finite element method. The influence of heating parameters and geometrical characteristics of the studied area on the formed temperature and velocity distributions of free convective fluid flow is researched. It is shown that the greatest influence on the process of natural convection in the considered conditions is exerted by the tube diameter. The obtained results can be used when considering liquid flows accompanied by free convection in installations with U-shaped tubes, such as in the thermoelectrokinetic effect.
1. Введение
Интерес к естественной конвекцией не ослабевает в настоящее время, поскольку процессы, сопровождающиеся ковекцией широко распространены в природных , и технических явлениях . Одним из наиболее известных и изученных примеров является конвекция Рэлея-Бенара, в которой при подогреве жидкости снизу образуются упорядоченные структуры, известные как ячейки Бенара.
В работе была высказана идея, что при протекании данного явления в вязкой электропроводящей среде, например, в плазме звезд в ней будут формироваться вихревые электромагнитные структуры, включающие вихревые поля сторонних сил и электрические токи. Согласно оценкам из этой работы, величина этих токов обеспечивает магнитную индукцию поля, соответствующую наблюдениям в области солнечных пятен на внешней конвективной границе Солнца.
Такие токи, возникающие в замкнутых структурах электропроводящей среды, являются примером перекрёстных явлений тепло-, массо- и электропереноса при участии трёх термодинамических сил. Данные явления впервые были теоретически предсказаны и названы термоэлектрокинетическими в . В последующем они были открыты и экспериментально изучены в растворах ионных электролитов , и коллоидных растворах с использованием экспериментальной установки в форме открытой системы в виде U-образной трубки. Перенос теплоты был вызван градиентом температуры, образовавшимся из-за подогрева U-образной трубки снизу. Поскольку массоперенос в электропроводящих средах осуществляется частицами, несущими электрический заряд, в одном из колен U-образной трубки скорость массопереноса направлена вдоль градиента температуры, а в другом – противоположно. Из-за различий подвижности заряженных частиц происходит их частичное разделение при прохождении через температурную неоднородность среды. В результате в электропроводящей среде образуется внутреннее электрическое поле и соответствующая разность потенциалов, которая была названа термоэлектрокинетической .
В условиях, когда вертикальный перепад температуры электролита, перемещающегося по U-образной трубке, образуется вследствие ее подогрева снизу, должны образовываться восходящие конвективные потоки. Эти потоки должны существенно увеличивать коэффициент теплопроводности среды и изменять режим ее течения. Действительно в на основе экспериментальных измерений и математического моделирования было показано, что из-за увеличенной теплопроводности за счет конвекции не удается достичь перепадов температуры по вертикали трубки более 5-6 °С.
В указанной работе расчет поля температур и скоростей покоящейся жидкости проводился на основе решения уравнений Навье-Стокса, неразрывности и теплопроводности в рамках метода конечных элементов. Построенная модель может послужить основой более общей и универсальной модели, пригодной для теоретического описания указанного класса перекрестных эффектов в вязких электропроводящих средах, например, в плазме звезд, в атмосфере и океанах планет и т.д. Кроме того возможности построенной модели не были использованы полностью, поэтому целью данной работы является уточнение модели и проведение на ее основе серии вычислительных экспериментов для определения влияния различных входных параметров экспериментальной установки на итоговое поле температуры и скорости.
Задача расчета поля температур и скоростей жидкости или газа при наличии свободной конвекции является сложной и допускает аналитическое решение лишь для ряда случаев с простой геометрией. Например, в случае жидкости, находящейся между двумя бесконечными стенками, имеющими разные температуры, в ней будут формироваться восходящее (вблизи теплой стенки) и нисходящее (вблизи холодной стенки) течения. Максимальная скорость течения будет пропорциональна числу Грасгофа
где L – характерный размер области, – кинематическая вязкость. При этом профиль температуры будет линейным .
В противоположном случае, когда стенки располагаются горизонтально, и при расположении более теплой стенки снизу, жидкость теряет стратификационную устойчивость и при значениях числа Рэлея
где a – коэффициент температуропроводности, больших 1708 в жидкости создается циркуляционные течения, называемые ячейками Рэлея-Бенара .
Также широко в литературе представлены результаты численного решения задачи развивающихся свободноконвективных течений жидкости, находящейся в квадратной или прямоугольной полости с разно нагретыми вертикальными стенками. В этом случае также удается получить стационарное решение задачи с развивающимся циркуляционным течением в полости, в котором вблизи нагретой стенки формируется поднимающееся течение и вблизи холодной – опускающееся.
Достаточно близкой к рассматриваемой нами задачей, которая была хорошо изучена в литературе, является задача о расчете поля температур и скорости жидкости, находящейся в цилиндрической трубке, подогреваемой снизу. Как показывают исследования, в этом случае в трубке формируется крупномасштабная циркуляция, которая распространяется на весь объем, если высота трубки равна ее диаметру . При этом формирующийся крупномасштабный вихрь с течением времени медленно меняет свою ориентацию в пространстве нерегулярным образом . Вихревому образованию оказались присущи т.н. осцилляции «плескания» и «скручивания», а само оно может на короткое время исчезать, а затем вновь формироваться, но уже в существенно иной пространственной ориентации. Указанные эффекты наблюдались экспериментально и также воспроизводились в результате численных расчетов .
Таким образом, целью нашей работы является разработка математической модели, с учетом эффектов естественной конвекции, тепло- и массо-переноса жидкости, находящейся в U- образной трубке, которая подогревается снизу. Проведение на основе модели вычислительных экспериментов с целью расчета полей температуры и скорости жидкости в данных условиях и оценка степени влияния естественной конвекции на процессы переноса в условиях термоэлектрокинетического эффекта. Также проведение серии расчетов с целью определения факторов, влияющих на величину температурного перепада и средней скорости свободно конвективных потоков жидкости, находящейся в данных условиях. Проведенные расчеты позволят определить оптимальные характеристики геометрии экспериментальной установки и условий нагрева, при которых величина термоэлектрокинетической ЭДС в электропроводящей среде максимизируется.
2. Методы и принципы исследования
Геометрия используемой в расчетах двумерной модели U-образной трубки представлена на рис. 1. Данную модель можно также рассматривать как U-образную полость, которая безгранично простирается в направлениях перпендикулярных плоскости рисунка. Полость заполнена жидкостью, верхние границы являются свободными границами жидкости, все остальные границы являются жесткими и скорость жидкости на них равна нулю. На границах 1-2 и 3-4 моделируется источник теплоты, эти границы являются эллиптическими кривыми, на остальных границах осуществляется теплообмен с окружающей средой. Трубка имеет отводы для ввода и вывода жидкости. При начальных условиях задачи жидкость находится в состоянии покоя, а ее температура равна температуре окружающей среды.
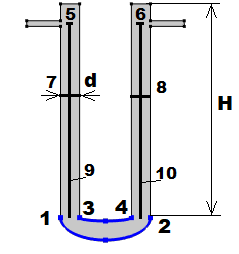
Рисунок 1 - Расчетная двумерная геометрическая область, моделирующая U-образную трубку:
H – высота колен; d – диаметр; 1-2, 3-4 – нагреваемые границы области; в точках 5, 6 производится расчет температуры с течением времени; вдоль линий 7, 8 и 9, 10 рассчитываются пространственные распределения температуры и скорости жидкости
В (3) – плотность и динамическая вязкость,
, p – скорость и давление, I – единичная матрица,
– поле объемных сил, действующих на жидкость. Данное уравнение, содержащее неизвестные поля скорости и давления, дополняется уравнением баланса массы
В случае неизотермических течений система уравнений переноса дополняется уравнением теплопроводности
где вектор теплового потока
В уравнениях (5), (6) Cp – теплоемкость при постоянном объеме, – коэффициент объемного расширения,
– тензор вязких напряжений, Q – мощность тепловых источников,
– коэффициент теплопроводности.
Система уравнений (3) - (5) с учетом (6) наиболее полно описывает возможные виды неизотермических течений в вязких сжимаемых средах и является существенно нелинейной. Одним из популярных упрощений системы уравнений тепло массопереноса при наличии естественной конвекции является приближение Буссинеска . Оно позволяет уменьшить нелинейность задачи путем упрощения системы уравнений и применимо, если изменение плотности мало.
При описании процессов с естественной конвекцией слагаемое с объемными силами равно силам плавучести, действующим на элемент жидкости , где учтена зависимость плотности от температуры и давления. В аппроксимации Буссинеска зависимость плотности от температуры учитывается в данном слагаемом и пренебрегается в остальных, в том числе в уравнении неразрывности, которое теперь выглядит
Допущение также приводит к тому, что в уравнении Навье-Стокса можно пренебречь членом и в предположении постоянной вязкости
слагаемое в скобках в правой части уравнения (3) преобразуется к
. Поскольку изменение давления мало, то можно пренебречь зависимостью плотности от давления в силовом члене и, раскладывая плотность в ряд Тейлора относительно средней плотности
по температуре, получаем
где
– коэффициент теплового расширения.
Наконец, пренебрегая указанными эффектами в уравнении теплопроводности, окончательно получаем уравнения математической модели неизотермического течения в приближении Буссинеска
Таким образом система нестационарных нелинейных уравнений (6)-(9) служит для расчета поля скоростей , температуры T(t,x,y) и давления p(t,x,y). Уравнения модели дополняются краевыми условиями.
В качестве начальных условий предполагается, что температура жидкости равна комнатной температуре а скорость жидкости равна нулю:
где – атмосферное давление.
Граничные условия для скорости и температуры выбирались следующим образом. Для всех границ кроме открытых верхних границ трубки использовались условия прилипания
На верхних открытых границах предполагается обращение в нуль компоненты скорости нормальной к границе
где – вектор нормали к границе. Границы 1-2, 3-4 рис. 1 имеют фиксированную температуру Th
На остальных границах, кроме открытых осуществляется конвективный теплообмен с окружающей средой
h – коэффициент теплоотдачи. На верхних открытых границах также реализуется конвективный теплообмен, но с другим коэффициентом теплоотдачи.
Для расчета математической модели был выбран метод конечных элементов, который в настоящее время широко применяется при решении задач тепло-, массо-переноса в твердых телах, жидкостях и газах . Производится дискретизация по пространственным и временным переменным. В нашем случае область моделирования разбивается с помощью узловых точек на множество треугольных элементов. Искомая функция, являющаяся решением физической задачи, записанной в виде системы дифференциальных уравнений в частных производных аппроксимируется линейной комбинацией базисных функций. Система исходных дифференциальных уравнений записывается в слабой, интегральной форме и после дискретизации уравнений получается система алгебраических уравнений для искомых функций в узловых точках.
3. Основные результаты
В расчетах используется геометрия, представленная на рис. 1. Исходные геометрические параметры: d = 17 мм, H = 19 см, расстояние между вертикальными коленами L = 8 см, длина отводов вверху l = 3 см, их диаметр d1 = 5 мм. Данные параметры также имеет экспериментальная установка, применявшаяся при исследовании термоэлектрокинетического эффекта, в дальнейшем они варьируются. Теплофизические, вязкостные свойства, плотность жидкости во всех расчетах соответствуют дистиллированной воде. Температура окружающей среды Text = 293 К, температура нагреваемых областей 1-2, 3-4 Th = 317 К, коэффициент теплоотдачи h = 50 Вт/м2К.
Расчеты по уравнениям модели показывают, что не удается достичь устойчивого стационарного решения в данной постановке задачи, что качественно согласуется с результатами расчетов и экспериментов для жидкости в цилиндрической трубке, подогреваемой снизу . Поэтому далее решается нестационарная задачи во временной области. Так на рис 2, 3 представлены пространственные распределения температуры и скорости жидкости в области моделирования.
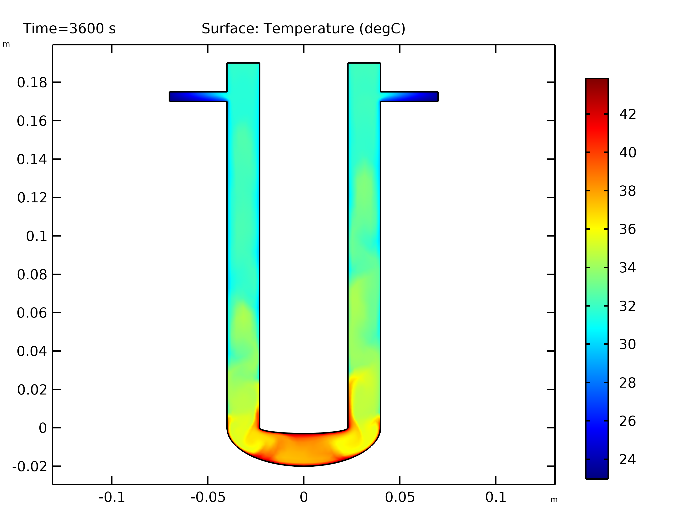
Рисунок 2 - Распределение поля температур дистиллированной воды для момента времени 3600 с
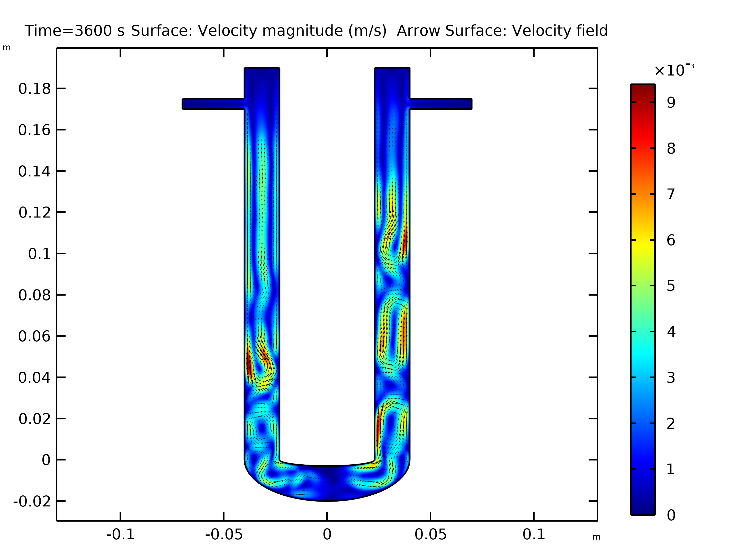
Рисунок 3 - Распределение поля скоростей дистиллированной воды для момента времени 3600 с
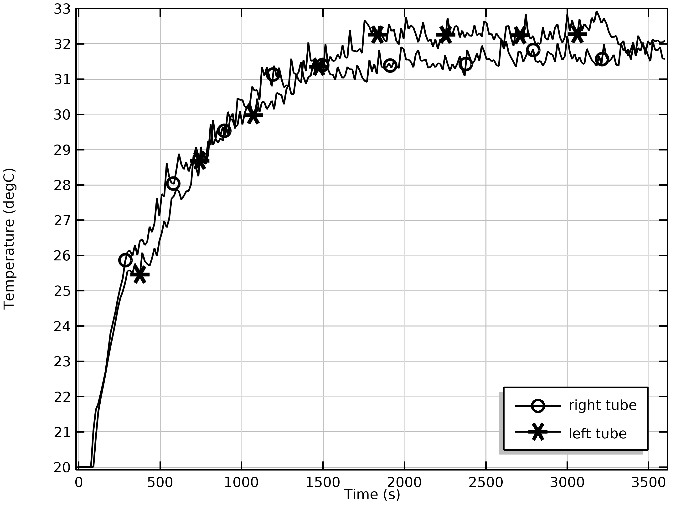
Рисунок 4 - Зависимость температуры жидкости от времени в точках 5 и 6
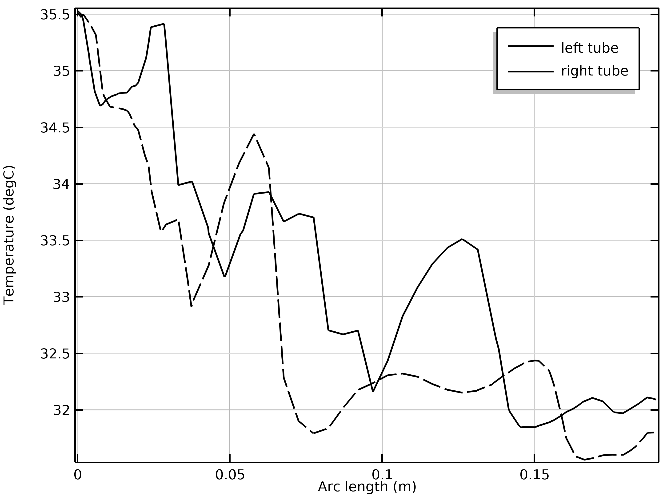
Рисунок 5 - Изменение температуры жидкости по вертикали трубки вдоль отрезков 7, 8
4. Обсуждение
Как следует из результатов расчета, температура жидкости в верхних частях U-образной трубки достигает стационарного значения 32°С, приблизительно через полчаса, при этом наблюдаются флуктуации температуры порядка 0.5 К рис. 4. Вследствие конвективного теплообмена перепад температуры по вертикали трубки для момента 3600 с не превосходит 3.5 К рис. 5, а разница температуры между областями жидкости, находящимися в нижней части изгиба и точками 5 или 6 составляет около 5 К. Полученные результаты подтверждаются экспериментально в работе , что свидетельствует об адекватности используемой модели. Также в жидкости возникают значительные восходящие конвективные потоки рис. 3, достигающие по абсолютной величине нескольких миллиметров в секунду. Причем в нижних частях колен трубки формируются крупномасштабные циркуляционные течения. Выше середины колен течение переходит к режиму, характеризующемуся движением жидкости вверх в центральных частях колен и опускному течению вблизи более холодных стенок. Полученные результаты качественно согласуются с известными в литературе. Среднее значение числа Рэлея, рассчитанное по формуле (2), для вертикальных колен трубки составляет величину порядка 108, что значительно выше критического значения для безграничной жидкости, находящейся между горизонтальными стенками с разной температурой.
Полученные результаты прежде всего свидетельствуют о том, что вследствие эффективного конвективного теплообмена при подогреве жидкости в U-образной трубке, в условиях термоэлектрокинетического эксперимента, трудно создать заметный перепад температуры. Также в жидкости должны формироваться значительные по величине конвективные течения, значения скорости которых могут быть сравнимы со скоростью течения среды в термоэлектрокинетическом эксперименте. В связи с этим в дальнейших расчетах была поставлена задача исследования влияния геометрических параметров области моделирования и температуры источника нагрева на интегральные характеристики поля температур и скоростей жидкости в исследуемой области. Для этого были проведены серии расчетов, в которых варьировались диаметр d и высота трубки H, а также температура нагреваемых областей 1-2, 3-4 Th.
В первой серии расчётов для исходной геометрии варьировалась температура нагреваемых областей Th при фиксированной температуре окружающей среды Text= 293 К. Результаты расчетов (установившийся перепад температуры вдоль трубки ΔT и среднее значение скорости свободно конвективного течения vm) приведены в таблице 1.
Таблица 1 - Результаты расчета для различных значений температуры нагреваемой области
Th, К | ΔT, К | vm, мм/с |
298 | 2,5 | 2,0 |
310 | 3,5 | 5,0 |
317 | 5,0 | 5,0 |
325 | 5,5 | 5,0 |
333 | 6,0 | 6,0 |
343 | 6,5 | 6,0 |
353 | 8,0 | 6,0 |
Как следует из результатов, температурный перепад по вертикали трубки слабо увеличивается с ростом температуры нагревателя, достигая значения 8 К при нагреве изгиба трубки до 80°С. В то же время, усредненное значение скорости свободно конвективного течения для значений температуры нагревателя выше 37°С практически не зависит от температуры нагреваемой области и составляет около 5-6 мм/с.
В следующей серии расчетов варьировалась высота вертикальной части колен U-образной трубки H, остальные параметры были как в исходном расчете. В таблице 2 приведены соответствующие результаты расчетов. Как следует из данных таб. 2 с ростом высоты трубки увеличивается величина перепада температуры по вертикали. Так, при увеличении длины трубки на 10 см, до 29 см, разница температур увеличивается почти в два раза до 9 К. Величина средней скорости конвективных потоков практически не зависит от высоты трубки.
Таблица 2 - Результаты расчета для различных значений высоты трубки H
H, см | ΔT, К | vm, мм/с |
9 | 2,5 | 4,5 |
14 | 3,5 | 4,5 |
19 | 5,0 | 5,0 |
24 | 6,0 | 4,5 |
29 | 9,0 | 4,5 |
Наконец в третьей серии расчетов варьировался диаметр трубки d, при этом значения остальных параметров были неизменными и соответствовали исходному расчету. В таблице 3 приведены результаты для данного случая.
Таблица 3 - Результаты расчета для различных значений диаметра трубки d
d, см | ΔT, К | vm, мм/с |
0,5 | 13,0 | 1,5 |
0,7 | 11,0 | 3,5 |
0,9 | 10,0 | 5,0 |
1,1 | 8,0 | 4,5 |
1,3 | 6,5 | 5,0 |
1,5 | 5,5 | 5,5 |
1,7 | 5,0 | 5,0 |
1,9 | 4,5 | 5,0 |
Как видно из таб. 3, изменение диаметра трубки существенно влияет на величину температурного перепада ΔT. Зависимость нелинейная, особенно сильно проявляющаяся, при малых диаметрах трубки менее 1,1 см. Также величина диаметра трубки единственный из рассмотренных параметров, который существенно влияет на скорость свободно конвективного течения. Однако эта зависимость проявляется лишь для значений диаметров менее 0,9 см. По-видимому, это связано с существенным увеличением роли вязкого трения и как следствие, снижением вклада конвекции в коэффициент теплопроводности жидкости, Указанный эффект может являться одной из причин сильной зависимости перепада температуры от диаметра трубки. Кроме того, диаметр трубки оказывает существенное влияние на качественный характер поля скоростей. Так, при значениях диаметра менее 0,9 см показанные ранее рис. 3 крупномасштабные циркуляционные течения в нижней части трубки не возникают.
Указанные закономерности были получены в приближении Буссинеска, в пренебрежении зависимостью плотности и вязкости от температуры и давления в уравнении теплопроводности и неразрывности. Безусловно в следующих исследованиях данная модель будет уточняться и усложняться, также будут учтены электрические эффекты.
5. Заключение
Таким образом, проведенные расчеты позволяют сделать следующие выводы.
1. Построена математическая модель в приближении Буссинеска, позволяющая рассчитывать методом конечных элементов поле температуры и скорости жидкости, находящейся в U-образной трубке при подогреве ее снизу. Впервые рассматривается геометрия с криволинейными, эллиптическими границами нижнего сгиба такой трубки. Результаты расчета в рамках модели подтверждаются экспериментальными измерениями по измерению поля температур и качественно согласуются с известными из литературы данными по расчету подобных задач близкой геометрии, что свидетельствует об адекватности используемой модели.
2. Серия проведенных расчетов с моделью позволила определить факторы, существенно влияющие на течение термоэлектрокинетического эффекта в электропроводящих жидкостях, и определить оптимальные способы, позволяющие увеличить термоэлектрокинетическую ЭДС. Температура нагреваемых областей, высота и диаметр U-образной трубки влияют на величину перепада температуры, от которого зависит величина термоэлектрокинетической ЭДС, как показано ранее . Причем наиболее эффективным способом увеличения эффективного перепада температуры является уменьшение диаметра трубки, позволяющее достигать значений перепадов, превышающих 10 К. Также уменьшением диаметра трубки при исследовании термоэлектрокинетического эффекта можно существенно снизить величину скорости свободно конвективных потоков, которые возникают в эксперименте при нагревании исследуемой жидкости в U-образной трубке снизу.
