SKIN EFFECT IN A CYLINDRICAL CIRCULAR CONDUCTOR WITH A RECTANGULAR PULSE SHAPE
СКИН-ЭФФЕКТ В ЦИЛИНДРИЧЕСКОМ ПРОВОДЕ КРУГЛОГО СЕЧЕНИЯ ПРИ ПРЯМОУГОЛЬНОЙ ФОРМЕ ИМПУЛЬСА ТОКА
Научная статья
Петрозаводский государственный университет, Петрозаводск, Россия
* Корреспондирующий автор (sasha.82[at]mail.ru)
АннотацияВ статье рассматривается случай скин-эффекта в проводнике при прямоугольной форме импульса тока на основании уравнений Максвелла. В работе определена величина падения напряжения на цилиндрическом проводнике в случае резкого скин-эффекта. Также получено выражение для эффективной глубины проникновения тока для прямоугольного импульса заданной длительности. На основании полученных выражений, приведен конкретный пример резкого скин-эффекта для цилиндрического медного проводника. Показано, что в случае резкого скин-эффекта снижаются требования к выбору материала проводника, а также слабо сказывается изменение длительности импульса. Полученные выражения также могут быть применены к проводнику кольцевого сечения.
Ключевые слова: скин-эффект, прямоугольная форма, импульс тока, глубина проникновения.
SKIN EFFECT IN A CYLINDRICAL CIRCULAR CONDUCTOR WITH A RECTANGULAR PULSE SHAPE
Research article
Tikhomirov A.A.*
Petrozavodsk State University, Petrozavodsk, Russia
* Corresponding author (sasha.82[at]mail.ru)
AbstractThe article deals with the case of the skin effect in a conductor with a rectangular shape of the current pulse based on the Maxwell's equations. The study determines the value of the voltage loss in a cylindrical conductor in the case of a sharp skin effect along with obtaining an expression for the effective depth of current penetration for a rectangular pulse of a given duration. Based on the obtained expressions, the study presents a specific example of a sharp skin effect for a cylindrical copper conductor. It is shown that in the case of a sharp skin effect, the requirements for the choice of the conductor material are reduced, while the change in the pulse duration has a low effect. The resulting expressions can also be applied to an annular conductor.
Keywords: Skin effect, rectangular shape, current pulse, penetration depth.
ВведениеРасчет скин-эффекта зависит от формы проводника, а также способа возбуждения в нем тока [1], [2]. Переходный процесс изменения плотности тока рассмотрен в [3], где показано смещение максимума тока от поверхности проводника в направлении его оси. Диффузии электромагнитного поля в массивные проводящие тела с произвольной гладкой поверхностью показана в [4], где методами пограничного слоя построено асимптотическое решение. Изменение плотности тока по радиусу проводника определяет неравномерность выделения тепловой энергии, что может находить применение в технике, например для предотвращения образования гололеда на линиях электропередач за счет пропускания по линии высокочастотной составляющей тока. Наличие скин-эффекта также влияет на величину активного сопротивления проводника и, следовательно, на потери энергии.
Наличие скин-эффекта влияет на величину активного сопротивления проводника и, следовательно, на потери энергии.
Для синусоидальной формы тока и проводника круглого сечения решение задачи распределения плотности тока не представляет особой сложности [5]. Однако в промышленности используются аноды больших размеров с возбужденным в них импульсным током близким к прямоугольной форме.
Распределение поля в проводниках круглого сечение может быть выражено через функции Бесселя и использовано для вычисления распространения поля вдоль проводника. Такой подход позволяет упростить расчеты и проводить широкий спектр исследований. В [6] показано, что форма проводника существенно влияет на скин-эффект, что должно быть учтено при его расчете. В работах [7] рассмотрен метод пограничного слоя для расчета электромагнитного поля в массивных проводниках любой формы.
Исходя из этого, актуальной задачей является рассмотрение случая резкого скин-эффекта, когда глубина проникновения тока гораздо меньше радиуса цилиндра, при приложении прямоугольного импульса напряжения. Целью настоящей работы является рассмотрение скин-эффекта в цилиндрического проводнике круглого сечения при приложении импульса прямоугольной формы методом, не связанным с необходимостью вычисления квадратур.
Так известно, что мощность джоулева тепла, выделяющаяся в цилиндре равна произведению площади поверхности цилиндра на величину вектора Пойтинга на этой поверхности (т.к. на боковой поверхности цилиндра вектор Пойтинга перпендикулярен к поверхности) [8].
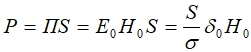 (1)
(1)
здесь ![]() значения плотности тока и напряженности магнитного поля на поверхности цилиндра; σ – проводимость материала цилиндра.
значения плотности тока и напряженности магнитного поля на поверхности цилиндра; σ – проводимость материала цилиндра.
Количество тепла, выделившееся в цилиндре за время t равно:
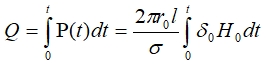 (2)
Значение величины
(2)
Значение величины 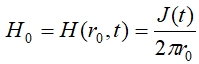 (3)
Для определения величины
(3)
Для определения величины 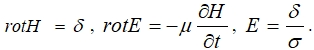 В цилиндрической системе координат при направлениях H и E как показано на рисунке 1 значения и будут следующие:
В цилиндрической системе координат при направлениях H и E как показано на рисунке 1 значения и будут следующие:
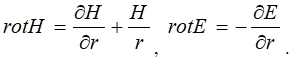
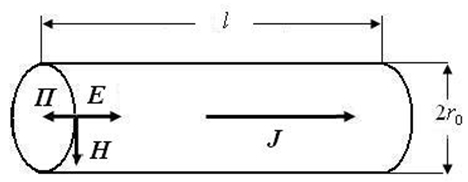
Рис. 1 – Направления магнитного и электрического полей в цилиндрическом проводнике
В случае малой глубины проникновения тока по сравнению с радиусом цилиндра ![]() задачу можно считать одномерной. Введем новую ось x направленную от какой-либо точки поверхности внутрь цилиндра. Тогда уравнения Максвелла запишутся:
задачу можно считать одномерной. Введем новую ось x направленную от какой-либо точки поверхности внутрь цилиндра. Тогда уравнения Максвелла запишутся:
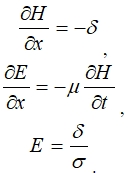 Разделяя переменные, получим отдельные дифференциальные уравнения для плотности тока и напряженности магнитного поля:
Разделяя переменные, получим отдельные дифференциальные уравнения для плотности тока и напряженности магнитного поля:
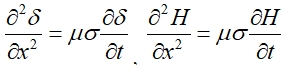 (4)
Граничные и начальные условия будут следующие:
(4)
Граничные и начальные условия будут следующие:
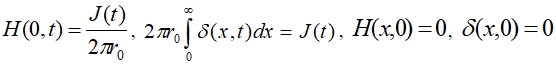 (5)
(5)
Так как более легкие граничные условия заданы для H, то удобнее сначала решать уравнение для H, а затем определять δ из выражения 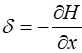 .
.
Решение уравнения для H типа (4) с граничными условиями (5) будет иметь следующий вид [9]:
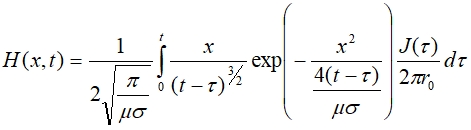 (6)
(6)
Для прямоугольного импульса ![]() , тогда решение упрощается [10]:
, тогда решение упрощается [10]:
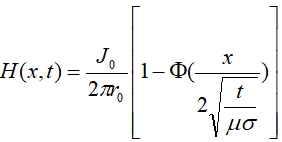 (7)
(7)
Здесь Ф – интеграл ошибок, значения которого имеются в таблицах:
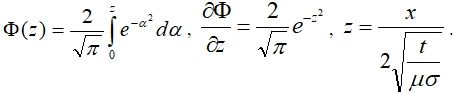
Для плотности тока δ получим следующее выражение:
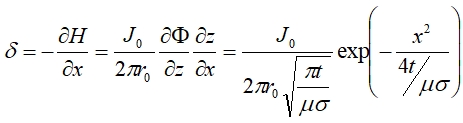 (8)
(8)
Проверка показывает, что решение (8) удовлетворяет уравнению (4) и граничному условию 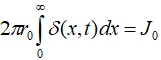 .
.
На поверхности цилиндра x=0 и
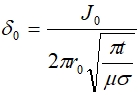 (9)
(9)
Основные результаты
Из выражения (9) видно, что для идеального прямоугольного импульса на переднем фронте плотность тока неограниченна на поверхности цилиндра. Однако это не приводит к расходящемуся интегралу для количества тепла:
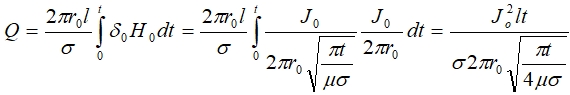 (10)
(10)
Таким образом, эффективная глубина проникновения тока для прямоугольного импульса длительностью τ равна:
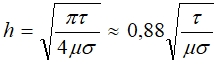 (11)
(11)
Как известно, для синусоидальной формы тока эффективная глубина проникновения тока равна:
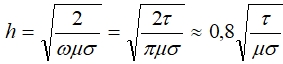 (12)
(12)
где τ – длительность полупериода. Как видно из (11) и (12) форма фронтов импульса незначительно влияет на эффективную глубину проникновения тока, следовательно, и на выделение тепла за счет омических потерь, если в формулу (10) для тока подставлять его эффективное значение 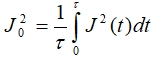 , τ – длительность импульса (для однополярного импульса).
, τ – длительность импульса (для однополярного импульса).
Однако влияние фронтов импульса можно учесть точно, если подставить в выражение (6) соответствующее значение ![]() .
.
Для ферромагнитных материалов уравнения Максвелла (4) становятся нелинейными, т. к. магнитная проницаемость среды зависит от величины напряженности магнитного поля. Как показал Л.Р. Нейман [11], эффективная глубина проникновения синусоидального тока в этих условиях несколько уменьшается и с большой точностью выражается следующей формулой 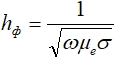 , где
, где ![]() – значение абсолютной магнитной проницаемости на поверхности проводника, определяемое действующим значением напряженности магнитного поля по кривой гистерезиса
– значение абсолютной магнитной проницаемости на поверхности проводника, определяемое действующим значением напряженности магнитного поля по кривой гистерезиса 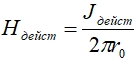 .
.
Эта формула весьма точна, если ![]() больше значения, при котором μ имеет максимум. При меньших значениях
больше значения, при котором μ имеет максимум. При меньших значениях ![]() формула может быть использована для ориентировочных расчетов. Для случая однополярного импульса
формула может быть использована для ориентировочных расчетов. Для случая однополярного импульса 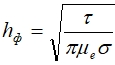 .
.
Определим величину падения напряжения на цилиндрическом проводнике длиной l при прямоугольной форме импульса при наличии резкого скин-эффекта.
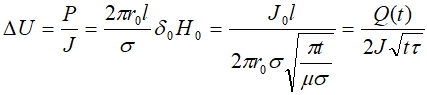 (13)
τ – длительность импульса.
(13)
τ – длительность импульса.
Как видно из формулы (13), падение напряжения на проводнике (без учета индуктивности) не постоянно и уменьшается во время импульса как![]() . На переднем фронте идеального прямоугольного импульса оно становится бесконечным. При реальных импульсах по формуле (13) можно рассчитывать падение напряжения во время импульса, начиная с окончания переднего фронта.
. На переднем фронте идеального прямоугольного импульса оно становится бесконечным. При реальных импульсах по формуле (13) можно рассчитывать падение напряжения во время импульса, начиная с окончания переднего фронта.
Рассмотрим конкретный пример, приведенных выше теоретических расчетов. Рассмотрим скин-эффект в медном проводнике, в случае резкого скин-эффекта. Длительность импульса примем ![]() , радиус проводника
, радиус проводника ![]() , длина проводника
, длина проводника ![]() . Тогда получим:
. Тогда получим:
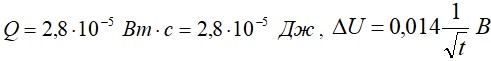 При произвольных размерах и материале проводника и размерах импульса тока, получим:
При произвольных размерах и материале проводника и размерах импульса тока, получим:
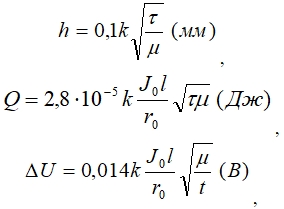 здесь τ – длительность импульса в мкс,
здесь τ – длительность импульса в мкс,
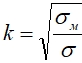 Для различных материалов значения k будут следующие (Таблица 1):
Для различных материалов значения k будут следующие (Таблица 1):
Таблица 1 – Значения для различных материалов
| Материал | Cu | W | Mo | Al | Ni | Сталь |
| 1 | 1,77 | 1,80 | 1,27 | 2,4 | 2,4 |
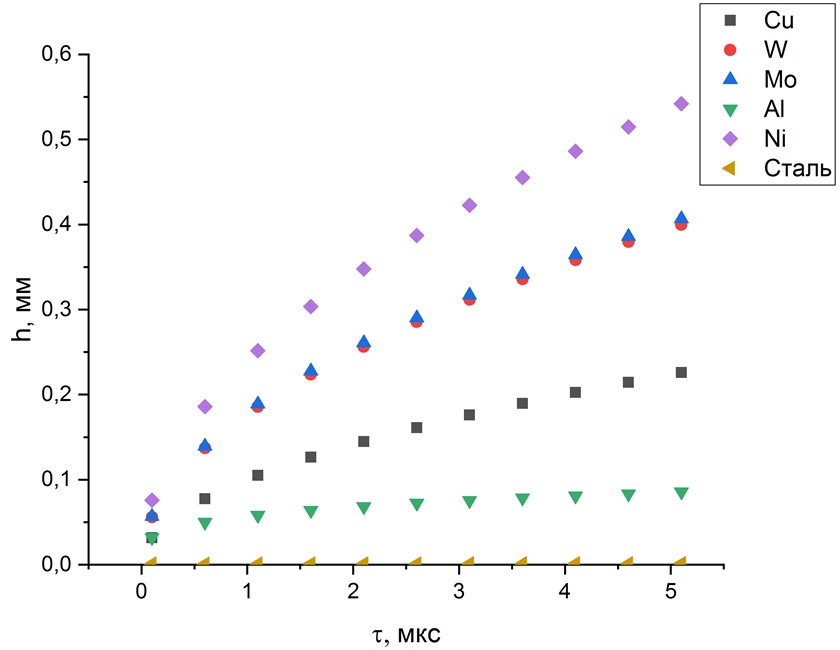
Приведем графические иллюстрации для сравнения соответствующих зависимостей при различных материалах проводника для условий рассмотренного примера. На рисунке 2 представлена зависимость глубины проникновения поля от длительности импульса.
Рис. 2 –Зависимость проникновения поля от величины длительности импульса тока
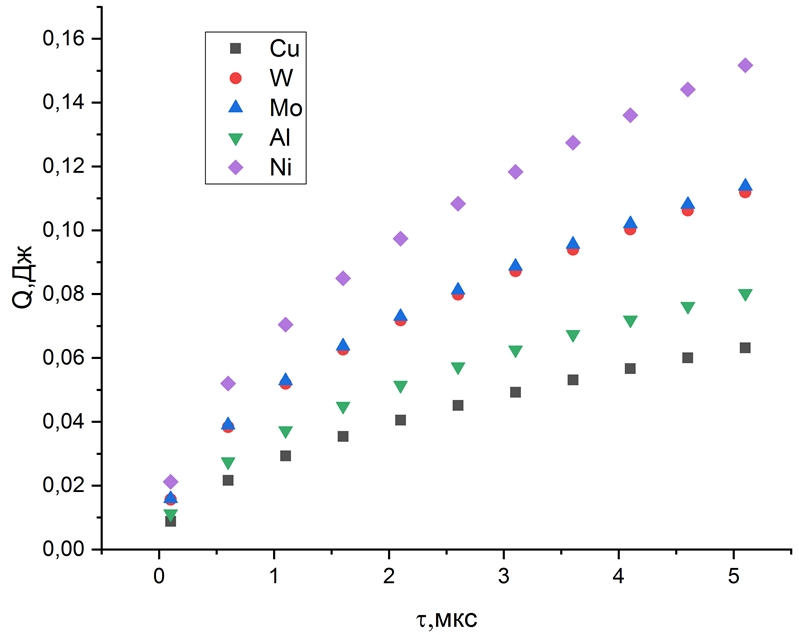
На рисунке 3 представлена зависимость выделяемой энергии от длительности импульса.Рис. 3 – Зависимость выделяемой энергии от длительности импульса тока
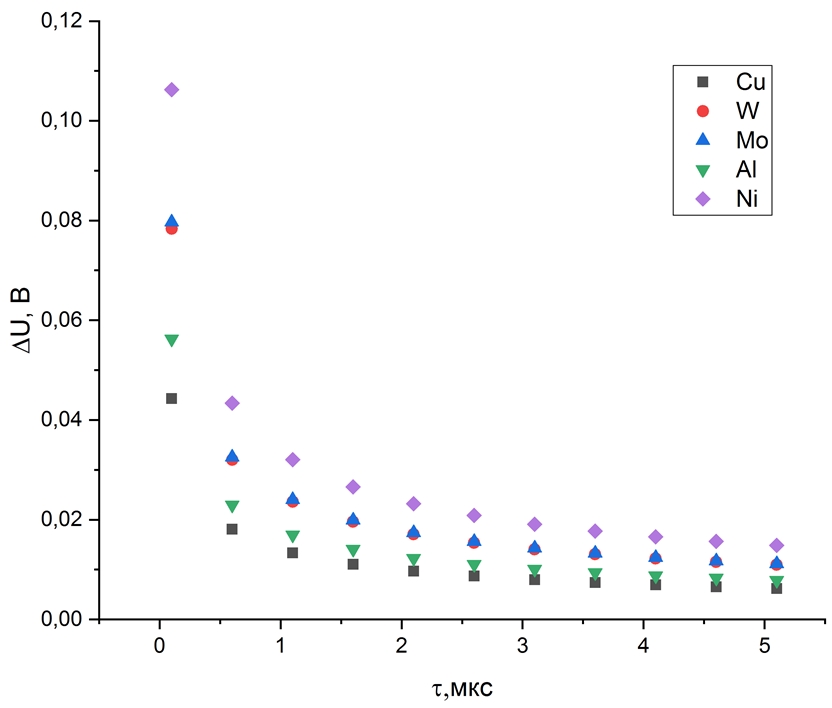
На рисунке 4 представлена зависимость падения напряжения от длительности импульса.Рис. 4 – Зависимость падения напряжения от длительности импульса тока
Все сказанное выше относится и к проводнику кольцевого сечения, если глубина проникновения тока h меньше толщины кольца.
Заключение
Интересным результатом полученных выражений (6), (11), (12) является то, что при резком скин-эффекте выделившееся тепло пропорционально величине 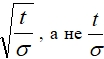 как при отсутствии скин-эффекта. А это означает, что снижаются требования к выбору материала проводника, и слабо сказывается изменение длительности импульса.
как при отсутствии скин-эффекта. А это означает, что снижаются требования к выбору материала проводника, и слабо сказывается изменение длительности импульса.
Так как обычно диаметр анода больше диаметра соединительных проводов, то если анод не ферромагнитный, омические потери в нем будут значительно меньше, чем в подводящих проводах.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Ломан В. А. Исследование влияния формы проводника на скин-эффект / В. А. Ломан, А. В. Ридель // Труды XIX Всероссийской научно-технической конференции Наука промышленность оборона 2018. – С. 73-75.
- Булгаков О. М.Учет скин-эффекта в проводниках с прямоугольным поперченным сечением / О. М. Булгаков, В. В. Лупандин, Б. К. Петров и др. // XV Международная научно-техническая конференция “Радиолокация, навигация, связь”. 2009 – С. 951-957.
- Козлов В. И. Скин-эффект в цилиндрическом проводнике / В. И. Козлов Физическое образование в Вузах 2002.– № 3 (8) – С .24-26.
- Каган В. И. Переходный процесс плотности тока в проводниках при скин эффекте / В. И. Каган // Электромагнитные волны и электронные системы 2009 – № 10 (14) – С. 62-64.
- Ландау Л. Д. Электродинамика сплошных сред / Л. Д. Ландау, Е. М. Лифшиц. Том VIII, Москва, «Наука», 1982.
- Фридман Б. Э. Скин-эффект в массивных проводниках электроимпульсных установок. Электромагнитное поле массивных проводников / Б. Э. Фридман, В. И. Каган // Журнал технической физики 2002– № 9 (72) –С. 44-51.
- Мищенко Е. Н. Скин-эффект в обмотках индукторов силовых устройств / Е. Н. Мищенко, В. Ф. Лопатин // Инновационные технологии в машиностроении, образовании и экономике, 2018 – № 4-1(10) – C.5-13.
- Фридман Б. Э. Поверхностный эффект в коаксиальных кабелях импульсных установок / Б. Э. Фридман, М. В. Медведев // Известия Российской академии наук. Энергетика 2019 – № 5 – С. 66-79.
- Тихонов А. Н. Уравнения математической физики / А. Н. Тихонов, А. А. Самарский. М. «Наука», 1960 г., 724 с.
- Нейман Л.Р. Поверхностный эффект в ферромагнитных телах / Л.Р. Нейман. М.; Л. : Госэнергоиздат, 1949, 376 c.
- Нейман Л.Р. Теоретическая электротехника: Избранные труды / Л.Р. Нейман Л. «Наука», 1988, 334 с.
Список литературы на английском языке / References in English
- Loman V. A. Issledovanie vlijanija formy provodnika na skin-ehffekt [Study of the Influence of the Shape of the Conductor on the Skin Effect] / V. A. Loman, A. V. Riedel // Trudy XIX Vserossijjskojj nauchno-tekhnicheskojj konferencii Nauka promyshlennost' oborona 2018 [Proceedings of the XIX All-Russian Scientific and Technical Conference Science Industry Defense 2018]. - pp. 73-75 [in Russian]
- Bulgakov O. M. Uchet skin-ehffekta v provodnikakh s prjamougol'nym poperchennym secheniem [Accounting for the Skin Effect in Conductors With a Rectangular Peppered Cross-Section] / O. M. Bulgakov, V. V. Lupandin, B. K. Petrov et al. // Mezhdunarodnaja nauchno-tekhnicheskaja konferencija “Radiolokacija, navigacija, svjaz'” [XV International Scientific and Technical Conference "Radar, Navigation, Communication". 2009]-pp. 951-957 [in Russian]
- Kozlov V. I. Skin-ehffekt v cilindricheskom provodnike [Skin Effect in a Cylindrical Conductor] / V. I. Kozlov // Fizicheskoe obrazovanie v Vuzakh 2002 [Physical Education in Higher Education Institutions 2002]. - No. 3 (8), pp. 24-26 [in Russian]
- Kagan V. I. Perekhodnyjj process plotnosti toka v provodnikakh pri skin ehffekte [Transient Process of Current Density in Conductors Under the Skin Effect] / V. I. Kagan // Ehlektromagnitnye volny i ehlektronnye sistemy [Electromagnetic Waves and Electronic Systems] 2009-No. 10 (14), pp. 62-64 [in Russian]
- Landau L. D. Ehlektrodinamika sploshnykh sred [Electrodynamics of Continuous Media Volume VIII] / L. D. Landau, E. M. Lifshitz, Moscow, Nauka, 1982 [in Russian]
- Friedman B. E. Skin-ehffekt v massivnykh provodnikakh ehlektroimpul'snykh ustanovok. Ehlektromagnitnoe pole massivnykh provodnikov [Skin Effect in Massive Conductors of Electric Pulse Installations. Electromagnetic Field of Massive Conductors] / V. I. Kagan // Zhurnal tekhnicheskojj fiziki [Journal of Technical Physics] 2002-No. 9 (72), pp. 44-51 [in Russian]
- Mishchenko E. N. Skin-ehffekt v obmotkakh induktorov silovykh ustrojjstv [Skin-Effect in the Windings of Inductors of Power Devices] / E. N. Mishchenko, V. F. Lopatin // Innovacionnye tekhnologii v mashinostroenii, obrazovanii i ehkonomike [Innovative Technologies in Mechanical Engineering, Education and Economics], 2018-No. 4-1 (10) - pp. 5-13 [in Russian]
- Fridman B. E. Poverkhnostnyjj ehffekt v koaksial'nykh kabeljakh impul'snykh ustanovok [Surface Effect in Coaxial Cables of Pulsed Installations] / B. E. Fridman // Izvestiya Rossiyskoy akademii nauk. Energetika [Bulletin of the Russian Academy of Sciences. Power Economy] 2019-No. 5-pp. 66-79 [in Russian]
- Tikhonov A. N. Uravnenija matematicheskojj fiziki [Equations of Mathematical Physics] / A. N. Tikhonov, A. A. Samarsky. M. "Nauka", 1960, 724 p. [in Russian]
- Neyman L. R. Poverkhnostnyjj ehffekt v ferromagnitnykh telakh [Surface Effect in Ferromagnetic Bodies] / L. R. Neyman. M.; L.: Gosenergoizdat, 1949, 376 p. [in Russian]
- Neyman L. R. Teoreticheskaja ehlektrotekhnika: Izbrannye trudy [Theoretical Electrical Engineering: Selected Works] / L. R. Neyman. "Nauka", 1988, 334 p. [in Russian]