A MATHEMATICAL MODEL OF ACNE
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ АКНЕ
Научная статья
Гончарова А.Б.1, *, Мазова А.В.2, Колпак Е.П.3
1, 2, 3 Санкт-Петербургский государственный университет, Санкт-Петербург, Россия
* Корреспондирующий автор (a.goncharova[at]spbu.ru)
АннотацияВ работе разработана математическая модель заболевания кожи – акне. В модели учитываются особенности возникновения, созревания и распространения пустул на системе потовых желез кожи. Процесс роста популяции бактерий описывается системой уравнений с дискретным временем. В модели лечения предполагается непосредственное влияние химических препаратов на пустулы. Статистико-вероятностный подход применен в модели распределения условных больных по времени наступления стадий заболевания и в моделях распределения по продолжительности лечения. Параметры, характеризующие кинетику роста пустул, скорость их распространения по поверхности определяются исходя из клинических данных. В модели лечения предполагается, что препараты воздействуют на все пустулы одновременно.
Ключевые слова: акне, псориаз, математическое моделирование, числовая последовательность, модель лечения, статистические методы.
A MATHEMATICAL MODEL OF ACNE
Research article
Goncharova A.B.1, *, Mazova A.V.2, Kolpak E.P.3
1, 2, 3 Saint Petersburg State University, Saint Petersburg, Russia
* Corresponding author (a.goncharova[at]spbu.ru)
AbstractThe current study develops a mathematical model of acne. The model takes into account the characteristics of the appearance, maturation, and spread of pustules on the system of sweat glands of the skin. The process of bacterial population growth is described by a system of discrete-time equations. The treatment model assumes the direct effect of chemicals on the pustules. The statistical-probabilistic approach is applied in the model of the distribution of patients by the time of the onset of the stages of the condition and in the models of the distribution by the duration of treatment. The parameters that characterize the kinetics of pustule growth and the rate of their spread over the surface are determined based on clinical data. The treatment model assumes that the drugs affect all the pustules simultaneously.
Keywords: acne, psoriasis, mathematical modeling, numerical sequence, treatment model, statistical methods.
Введение
Из многочисленных заболеваний кожи акне не является заболеванием, приводящим к необратимым изменениям в организме [1]. Наибольшую когорту пациентов этой болезни образуют лица в возрасте до 30 лет. Акне по данным рандомизированных исследований наблюдается у 50-90% лиц подросткового возраста [2]. Болезнь поражает поверхность кожи, изменяет у молодежи представление о собственной непривлекательности, вызывает психические нарушения, пагубно влияет на психику, приводит к депрессии, снижает самооценку и качество жизни. Значимыми экспосом-факторами в молодежной популяции являются стресс, нарушение диеты, изменение климатических условий в местах постоянного проживания, связь c менструальным циклом. В целом заболевание рассматривается как медико-социальная проблема. Запоздалое обращение за медицинской поддержкой или самолечение могут привести к длительной процедуре лечения, а в отдельных случаях и к тяжелым последствиям. Акне может стать хроническим рецидивирующим воспалительным заболеванием продолжительностью в нескольких лет, с длительными и частыми рецидивами, трудно поддающихся терапии [3].
Возникновение заболевания
Кожа представляет собой многослойное образование, поверхность которого покрыта порами. В корне волоса кожного покрова находится волосяной фолликул с прилегающими к нему сальными железами. Секрет, который образуется в сальной железе, выходит на поверхность кожи. При заболевании акне пора закупоривается, и секрет остаётся и накапливается в волосяном фолликуле, сальной железе, создавая питательную среду для размножения бактерий. Причинами закупорки пор может быть нарушение процесса отшелушения верхнего слоя кожи, изменение состава секрета. В результате медленнорастущая бактерия Propionibacterium acne получает избыточное питание и начинает быстро размножаться.
Заболевание сопровождается открытыми и закрытыми воспалительными поражениями кожи в виде папул, пустул, угрей. Повреждение сальной железы сопровождается проникновением секрета и бактерий в межклеточное пространство. Это может привести не только к повторному возникновению заболевания, но и к более тяжелым последствиям. Заболевание условно разделяется на четыре стадии. К первой стадии заболевания относят поражение кожи 1-10 пустулами, к второй ‑ 10-20, к третьей – 20-30, к четвертой – более 40 [4], [5].
Основным методом лечения акне является медикаментозное лечение. При лечении папуло-пустулезных акне легкой и средней степени тяжести используются препараты, подавляющие путем ингибирования биохимические реакции, поддерживающие воспалительный процесс [6].
Лечение может представлять определенные трудности, несмотря на широкий арсенал препаратов, и различных схем лечения, при этом ни одна из них не может считаться терапией выбора. Возможен и кратковременный терапевтический эффект, обусловленный отсутствием воздействия препаратов на иммуногенез заболевания.
Модель образования пустулы
Математические модели кожных заболеваний, за исключением меланомы, практически отсутствуют, несмотря на наличие биохимических моделей [7]. В большинстве математических моделей различных процессов в распределенных в пространстве тканях используется аппарат интегрального и дифференциального исчисления. Акне распространяется в виде точечной системы пустул и папул, случайным образом распределенных по поверхности кожи. Поэтому более естественна модель акне как процесса роста отдельной пустулы, по мере «созревания» которой могут зарождаться новые пустулы на некотором удалении от «созревшей» [8].
Пусть размножение бактерий в волосяном фолликуле происходит в режиме дискретного времени с временным интервалом τ. Пусть количество бактерий![]() на каждом временном интервале
на каждом временном интервале ![]() увеличивается на величину
увеличивается на величину
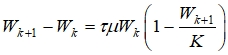 (1)
(1)
где μ ‑ параметр, K ‑ максимальное количество бактерий, которое может находиться в фолликуле. На первом такте размножения бактерий считается, что ![]() .
.
Параметр μ определяется исходя из данных по кинетике размножения бактерий. В уравнении (1) можно принять, что K=1. То есть за единицу измерения при такой нормировке количества бактерий принимается максимальное количество бактерий, которые могут содержаться в фолликуле.
В модели (1) считается, что прирост численности бактерий пропорционален их количеству (множитель ![]() в правой части уравнения (1)) и доле незаполненного бактериями их функционального пространства K (множитель
в правой части уравнения (1)) и доле незаполненного бактериями их функционального пространства K (множитель ![]() в (1)). Считается также, что размножение бактерий происходит на неограниченном пищевом ресурсе.
в (1)). Считается также, что размножение бактерий происходит на неограниченном пищевом ресурсе.
Из уравнения (1) следует, что количество бактерий на k+1 такте размножения подсчитывается по формуле
![]() (2)
(2)
Поскольку ![]() , то для любого
, то для любого ![]() выполняется неравенство
выполняется неравенство
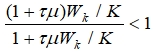
Поэтому последовательность (2) будет сходиться к неподвижной точке: ![]() .
.
Лечение акне осуществляется непосредственным воздействием на бактерии. Одним из вариантов является применение химических препаратов. Химические препараты вводятся в модель (1) следующим образом
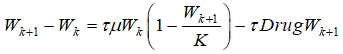 (3)
(3)
где Drag ‑ количество химических препаратов, уничтожающих бактерии в фолликуле на временном интервале τ.
В клинической практике диагноз ставится на момент обращения пациента за медицинской помощью. При этом от начала заболевания может пройти m тактов в процессе образования пустул. Тогда согласно (2) и (3) до такта m рост численности бактерий описывается соотношением (2), а начиная с такта m+1 соотношением
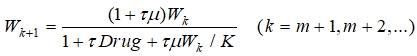 (4)
(4)
Последовательность (4) будет сходиться к стационарной точке ![]() и к стационарной точке
и к стационарной точке ![]() , если выполняется неравенство
, если выполняется неравенство ![]() . Последнее неравенство является условием полного уничтожения бактерий.
. Последнее неравенство является условием полного уничтожения бактерий.
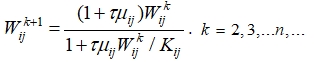 (5)
где
(5)
где 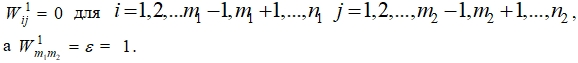
Распространение пустул происходит случайным перемещением части бактерий от одного фолликула к другому при условии, что в материнском фолликуле количество бактерий превысило некоторое «пороговое» значение ![]() на временном такте k. То есть, с четом (5), часть бактерий из фолликула с номером ij случайным образом «переселяется» в фолликул с номером ml:
на временном такте k. То есть, с четом (5), часть бактерий из фолликула с номером ij случайным образом «переселяется» в фолликул с номером ml:
если 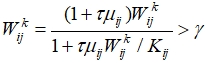 , то
, то
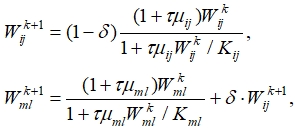
где ![]() ‑ доля бактерий фолликула ij, переместившихся в фолликул ml. Количество бактерий в пустулах в момент kτ подсчитывается по формуле:
‑ доля бактерий фолликула ij, переместившихся в фолликул ml. Количество бактерий в пустулах в момент kτ подсчитывается по формуле: ![]() .
.
Модель статистики заболевания
Параметр μ в (1) выбирается исходя из скорости появления новых пустул. Носитель пустул обращается за медицинской помощью на первой или второй стадии заболевания. Поэтому оценить дату начала заболевания сложно. Отслеживание кинетики роста пустул невозможно, поскольку пациента необходимо лечить. Оценку значения параметра μ можно сделать по повторному проявлению заболевания после окончания лечения [9]. По данным клинических исследований после лечения рецидив может наступить через 40-50 дней. Если принять, что повторное развитие заболевания фиксируется при появлении 2-3 пустул, то в этом случае из (6) находится значение параметра ![]() 1/день. Параметр τ в этом случае соответствует дискретному времени длительностью в 1 день, т.е.
1/день. Параметр τ в этом случае соответствует дискретному времени длительностью в 1 день, т.е. ![]() .
.
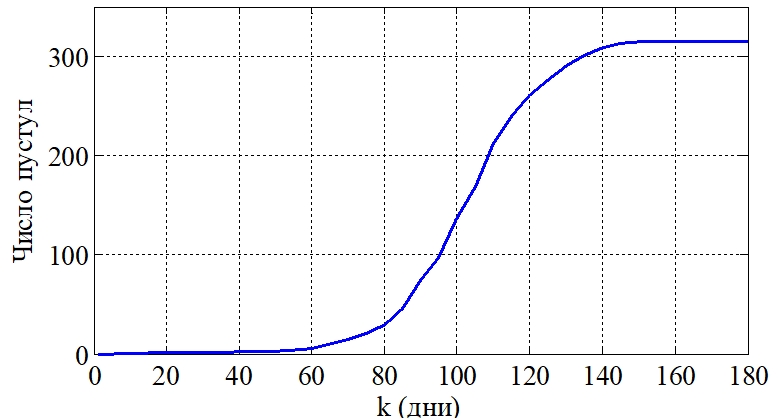
На рис. 1 отражено изменение числа пустул во времени. Расчетный инкубационный» период созревания одной пустулы – 10 дней. Время появления новой пустулы на первой стадии заболевания ‑ 2-4 дня, а со временем может появляться ежедневно несколько пустул. Третья стадия заболевания при значении ![]() наступает на 60-й день [3], [4].
наступает на 60-й день [3], [4].
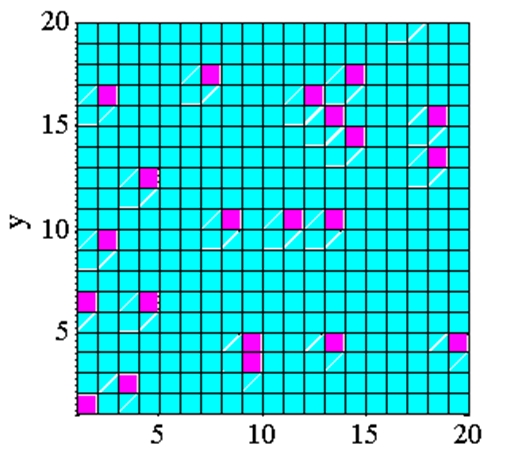
На рис.2 приведен вариант распределения пустул на поверхности вначале третьей стадии заболевания.
Рис. 1 – Динамика изменения числа пустул
Рис. 2 – Распределение пустул на поверхности вначале третьей стадии «заболевания»
Последовательностям ![]() при различных значениях параметров
при различных значениях параметров ![]() соответствует динамика роста числа пустул у разных «больных». Поэтому, выбирая параметры
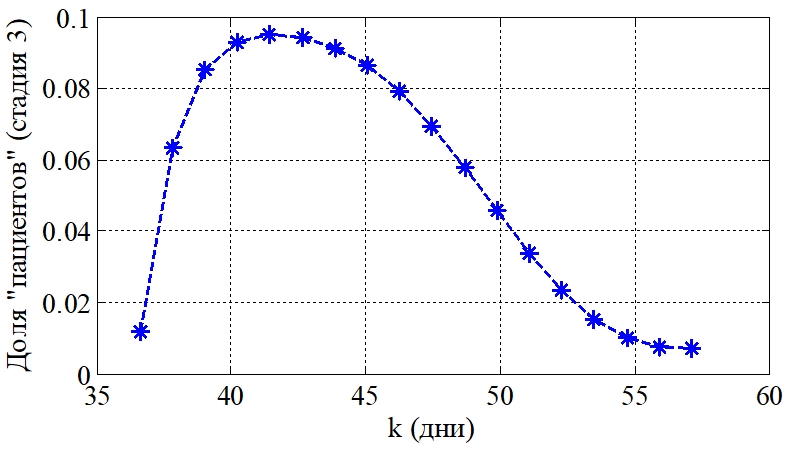
соответствует динамика роста числа пустул у разных «больных». Поэтому, выбирая параметры ![]() случайным образом из заданного диапазона, можно оценить распределение больных по времени достижения заданного количества пустул. На рис. 3 отражено распределение 30 000 условных «больных» по времени наступления третьей стадии заболевания (образование 20 пустул) для выбранных случайным образом параметров
случайным образом из заданного диапазона, можно оценить распределение больных по времени достижения заданного количества пустул. На рис. 3 отражено распределение 30 000 условных «больных» по времени наступления третьей стадии заболевания (образование 20 пустул) для выбранных случайным образом параметров ![]() .
.
Рис. 3 – Распределение 30 000 «пациентов» по времени наступления третьей стадии (20 пустул) «заболевания»
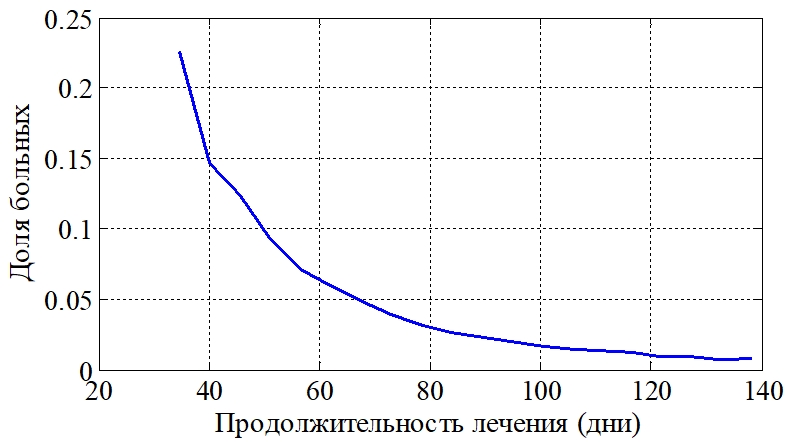
На рис. 4 отражено распределение больных по времени лечения. В модели влияния препаратов на количество бактерий (4) предполагалось, что препараты воздействует на все пустулы одновременно. Лечение считалось законченным, если для всех ![]() при некотором значении k выполнялось неравенство
при некотором значении k выполнялось неравенство ![]() для
для ![]() . Параметр Drug=0.3 выбирался исходя из клинических данных, приведенных в [10], [11], согласно которым среднее время лечения составляло около 60 дней.
. Параметр Drug=0.3 выбирался исходя из клинических данных, приведенных в [10], [11], согласно которым среднее время лечения составляло около 60 дней.
Рис. 4 – Распределение «больных» по продолжительности «лечения»
ЗаключениеПредложенная модель акне и его лечения, основанная только на кинетике собственного роста популяции бактерий, согласуется с клиническими данными по времени наступления стадий заболевания и продолжительности лечения. Теоретические зависимости по этим характеристикам дают возможность определить специалистам временные интервалы принятия решений, схемы лечения и оценить их эффективность.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Самцов А. В. Акне и акнеформные дерматозы / А. В. Самцов. М: Из-во Фармтека. 2014. 352.
- Дрождина М.Б. Возрастные корреляции вульгарных акне. Сравнительное исследование микробиома и экспосома акне у студентов Кировского ГМУ. Анализ результатов терапии применительно к показателям качества жизни / М.Б. Дрождина, Е.П. Колеватых, М.А. Трубникова и др. // Вестник дерматологии и венерологии. - 2020. - T. 96. - № 4. -С. 32-42.
- Сорокина Е.В. Комбинированная терапия инверсных акне с учетом особенностей иммунного ответа и микробиоты кожи / Е.В. Сорокина, С.А. Масюкова, Э.А. Ахматова и др. // Дерматология в России. – 2018. - (Прил. 1). - С. 151-153.
- Круглова Л.С. Актуальные вопросы терапии больных акне / Л.С. Круглова, Н.В. Грязева, Э.М. Гешева // Кремлевская медицина. Клинический вестник. - 2019. - №1. - С. 122-128.
- Проценко Т.В. Акне: от теории к практическим рекомендациям // Научно-практический журнал по дерматологии, венерологии, косметологии «Торсуевские чтения». – 2019. - №4 (26). - С. 62-67.
- Самцов А.В. Новые технологии в комбинированной топической терапии акне / А.В. Самцов // Вестник дерматологии и венерологии. – 2020. - 96 (3): - 75-79.
- Gilmore, S. Modelling skin disease: Lessons from the worlds of mathematics, physics and computer science (Review) / Gilmore // Australasian Journal of Dermatology. – 2005. – V. 46. - № 2. – P. 61-69. DOI:0.1111/j.1440-0960.2005.00143.x. PubMed: 15842395.
- Frederick Frasch H.F. Application of numerical methods for diffusion-based modeling of skin permeation / H.F. Frederick Frasch, A.M. Barbero // Advanced Drug Delivery Reviews. – 2013. - V. 65. – P. 208-220. DOI: 1016/j.addr.2012.01.001.
- Тонеева Д.В. Алгоритм построения экспертной системы диагностики заболеваний на основе дифференциально-диагностических признаков / Д.В. Тонеева, А.Б. Гончарова, Е.И. Сергеева // Технические науки - от теории к практике. - 2016. - № 11 (59). - С. 37-43.
- Zhang, Y. An herbal cream reduces erythema of sensitive skin / Zhang, Y. Jin, P. Humbert et al. // Journal of Cosmetic Dermatology. 2021. – V. 20. – №3. – P. 792-797. DOI: 10.1111/jocd.13610. PubMed: 32710585.
- Фйзуллина Е.В. Лечение акне, осложненного сопутствующей микобиотой / Е.В. Фйзуллина, И.М. Хисматулина, А.М. Гордеева // Проблемы медицинской микологии. – 2019. - Т.21. - №4. - С. 30-33.
Сисок литературы на английском языке / References in English
- Samtsov. V. Akne i akneformnye dermatozy [Acne and Acneform Dermatoses] / V. Samtsov. M: Farmteka. 2014. 352 [in Russian]
- Drozhdina M. B. Vozrastnye korreljacii vul'garnykh akne. Sravnitel'noe issledovanie mikrobioma i ehksposoma akne u studentov Kirovskogo GMU. Analiz rezul'tatov terapii primenitel'no k pokazateljam kachestva zhizni [Age-Related Correlations of Vulgar Acne. Comparative Study of the Microbiome and Exposome of Acne in Students of the Kirov State Medical University. Analysis of the Results of Therapy in Relation to Quality of Life Indicators] / M. B. Drozhdina, E. P. Kolevatykh, M. A. Trubnikova et al. // Vestnik dermatologii i venerologii [Bulletin of Dermatology and Venereology]. - 2020. - Vol. 96. - No. 4. - pp. 32-42. [in Russian]
- Sorokina E. V. Kombinirovannaja terapija inversnykh akne s uchetom osobennostejj immunnogo otveta i mikrobioty kozhi [Combination Therapy of Inverse Acne, Taking Into Account the Characteristics of the Immune Response and the Microbiota of the Skin] / E. V. Sorokina, S. A. Masyukova, E. A. Akhmatova et al. // Dermatologija v Rossii [Dermatology in Russia]. - 2018. - (Appendix 1). - pp. 151-153 [in Russian]
- Kruglova L. S. Aktual'nye voprosy terapii bol'nykh akne [Actual Issues of Therapy of Patients With Acne] / L. S. Kruglova, N. V. Gryazeva, E. M. Gesheva // Kremlevskaja medicina. Klinicheskijj vestnik [Kremlin Medicine Journal]. - 2019. - No. 1. - p. 122-128 [in Russian]
- Protsenko T. V. Akne: ot teorii k prakticheskim rekomendacijam [Acne: From Theory to Practical Recommendations] / T. V. Protsenko // Nauchno-prakticheskijj zhurnal po dermatologii, venerologii, kosmetologii «Torsuevskie chtenija» [Scientific and Practical Journal of Dermatology, Venereology, Cosmetology "Torsuev Readings"]. – 2019. - №4 (26). - pp. 62-67 [in Russian]
- Samtsov A.V. Novye tekhnologii v kombinirovannojj topicheskojj terapii akne [New Technologies in Combined Topical Therapy of Acne] / A. V. Samtsov // Vestnik dermatologii i venerologii [Bulletin of Dermatology and Venereology]. – 2020. - 96 (3): - 75-79. [in Russian]
- Gilmore, S. Modelling skin disease: Lessons from the worlds of mathematics, physics and computer science (Review) / Gilmore // Australasian Journal of Dermatology. – 2005. – V. 46. - № 2. – P. 61-69. DOI:0.1111/j.1440-0960.2005.00143.x. PubMed: 15842395.
- Frederick Frasch H.F. Application of numerical methods for diffusion-based modeling of skin permeation / H.F. Frederick Frasch, A.M. Barbero // Advanced Drug Delivery Reviews. – 2013. - V. 65. – P. 208-220. DOI: 1016/j.addr.2012.01.001.
- Toneeva D. V. Algoritm postroenija ehkspertnojj sistemy diagnostiki zabolevanijj na osnove differencial'no-diagnosticheskikh priznakov [Algorithm for Constructing an Expert System for Diagnosing Diseases Based on Differential Diagnostic Signs] / D. V. Toneeva, A. B. Goncharova, E. I. Sergeeva // Tekhnicheskie nauki - ot teorii k praktike [Technical Sciences: From Theory to Practice]. - 2016. - № 11 (59), pp. 37-43 [in Russian]
- Zhang, Y. An herbal cream reduces erythema of sensitive skin / Zhang, Y. Jin, P. Humbert et al. // Journal of Cosmetic Dermatology. 2021. – V. 20. – №3. – P. 792-797. DOI: 10.1111/jocd.13610. PubMed: 32710585.
- Fizullina E. V. Lechenie akne, oslozhnennogo soputstvujushhejj mikobiotojj [Treatment of Acne Complicated by Concomitant Mycobiota] / E. V. Faizullina / I. M. Khismatulina, A. M. Gordeeva // Problemy medicinskojj mikologii [Problems of Medical Mycology]. - 2019. - Vol. 21. - No. 4, pp. 30-33 [in Russian]