ВЫЯВЛЕНИЕ ЛАТЕНТНОГО ФАКТОРА ПРИ ИССЛЕДОВАНИИ СТРУКТУРЫ ДАННЫХ
ВЫЯВЛЕНИЕ ЛАТЕНТНОГО ФАКТОРА ПРИ ИССЛЕДОВАНИИ СТРУКТУРЫ ДАННЫХ
Научная статья
Двоерядкина Н.Н.¹, Чалкина Н.А.²
1, 2 Амурский государственный университет, Благовещенск, Россия
Аннотация
В статье рассматривается возможность применения многомерного факторного анализа для выявления латентных характеристик при проведении педагогического исследования.
Ключевые слова: корреляция, латентный фактор, факторные нагрузки, факторные весы.
Keywords: correlation, latent, factor loading, factor scopes.
В своей профессиональной деятельности социальные педагоги обязательно используют математические методы для познания социальных явлений. Однако, из-за противоречия, возникающего между формализмом математики и реальными происходящими в обществе процессами, интересующими социального педагога, им необходимо либо адаптировать математические методы для своих нужд, либо, базируясь на известных методах математики, разрабатывать новые методы, специально приспособленные для решения различных социологических задач.
Собирая данные для педагогического исследования, исследователь руководствуется определенными гипотезами, информация относится к избранным предмету и теме исследования, но нередко она представляет собой сырой материал, в котором нужно изучить структуру показателей, характеризующих объекты, выявить однородные группы объектов. Если объект исследования сложен и обладает сразу множеством качественных и количественных признаков взаимосвязанных между собой, то возникает необходимость соединить их в одну совокупную характеристику, а затем осуществить анализ полученной системы в интересующем исследователя направлении, учитывая особенности каждого признака в отдельности и специфику всей совокупности в целом. Такая работа может быть осуществлена с помощью факторного анализа.
Идея метода факторного анализа состоит в возможности сконцентрировать исходную информацию, выражая большое число рассматриваемых признаков через меньшее число более емких внутренних характеристик явления, которые не поддаются непосредственному измерению. Задачами факторного анализа являются: сокращение числа переменных (редукция данных) и определение структуры взаимосвязей между переменными, т.е. классификация переменных.
Материалом для факторного анализа служат корреляционные связи, которые вычисляются между переменными, включенными в обследование. Главное понятие факторного анализа – фактор. Это искусственный статистический показатель, возникающий в результате специальных преобразований таблицы коэффициентов корреляции между изучаемыми признаками.
Основные результаты факторного анализа выражаются в наборах факторных нагрузок и факторных весов. Факторные нагрузки – это значения коэффициентов корреляции каждого из исходных признаков с каждым из выявленных факторов. Чем теснее связь данного признака с рассматриваемым фактором, тем выше значение факторной нагрузки.
Факторными весами называют количественные значения выделенных факторов для каждого из имеющихся объектов. Объекту с большим значением факторного веса присуща большая степень проявления свойств, определяемых данным фактором. Положительные факторные веса соответствуют тем объектам, которые обладают степенью проявления свойств больше средней.
Данные о факторных нагрузках позволяют сформулировать выводы о наборе исходных признаков, отражающих тот или иной фактор, и об относительном весе отдельного признака в структуре каждого фактора. Данные о факторных весах определяют ранжировку объектов по каждому фактору.
Набор методов факторного анализа в настоящее время достаточно велик, насчитывает десятки различных подходов и приемов обработки данных. Результаты факторного анализа будут успешными, если удается дать содержательную интерпретацию выявленных факторов, исходя из смысла показателей, характеризующих эти факторы. Данная стадия работы весьма ответственная; она требует от исследователя четкого представления о содержательном смысле показателей, которые привлечены для анализа и на основе которых выделены факторы. Алгоритмы факторного анализа отличаются, трудоемкостью, их полное выполнение возможно при условии использования технических средств.
Рассмотрим использование факторного анализа для выявления латентных факторов на условном примере.
При переходе школьников из начальной школы в классы среднего звена решено организовать несколько профильных классов. В связи с этим социальному педагогу поручено разработать систему тестов для младших школьников, с помощью которых можно определить способности ребенка. Фрагмент результатов тестов приведен в таблице 1.
Таблица 1 Исходные данные
|
Рост, см |
Вес, кг |
Память на числа |
Логическое мышление |
Техника чтения |
фантазия |
Прыжки в длину |
|
|
И.П. |
150 |
35 |
7 |
есть |
180 |
нет |
70 |
|
К.Р. |
156 |
34 |
6 |
нет |
156 |
есть |
120 |
|
М.Ш. |
168 |
32 |
5 |
есть |
189 |
нет |
140 |
|
Д.Е. |
160 |
39 |
2 |
нет |
190 |
есть |
80 |
|
Ю.Г. |
162 |
45 |
4 |
нет |
200 |
есть |
90 |
|
Т.Р. |
159 |
30 |
5 |
нет |
230 |
нет |
100 |
|
К.Л. |
145 |
28 |
9 |
есть |
250 |
есть |
120 |
|
О.М. |
150 |
32 |
7 |
есть |
200 |
нет |
110 |
|
П.Н. |
160 |
25 |
7 |
есть |
180 |
нет |
100 |
На первом этапе необходимо стандартизировать исходные данные и определить коэффициенты корреляции Пирсона между всеми переменными (табл.2).
Таблица 2. Корреляционная матрица
|
рост |
вес |
Память на числа |
Логическое мышление |
Техника чтения |
Фантазия |
Прыжки в длину |
|
| Рост |
1,00 |
0,26 |
-0,70 |
-0,34 |
-0,36 |
-0,12 |
0,18 |
| Вес |
0,26 |
1,00 |
-0,67 |
-0,58 |
-0,23 |
0,50 |
-0,42 |
| Память |
-0,70 |
-0,67 |
1,00 |
0,71 |
0,27 |
-0,24 |
0,30 |
| Логическое мышление |
-0,34 |
-0,58 |
0,71 |
1,00 |
0,11 |
-0,55 |
0,25 |
| Техника чтения |
-0,36 |
-0,23 |
0,27 |
0,11 |
1,00 |
0,06 |
0,12 |
| Фантазия |
-0,12 |
0,50 |
-0,24 |
-0,55 |
0,06 |
1,00 |
-0,04 |
| Прыжки в длину |
0,18 |
-0,42 |
0,30 |
0,25 |
0,12 |
-0,04 |
1,00 |
Для определения оптимального количества латентных факторов необходимо найти собственные числа корреляционной матрицы путем решения уравнения: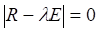 
. Определить сколько % дисперсии объясняет каждое собственное число: 
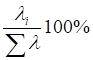и вычислить накопленный процент (табл.3).
Таблица 3. Анализ собственных чисел
|
Собственные числа |
% объясненной дисперсии |
Накопленный % |
|
3,071116 |
43,87308 |
43,8731 |
|
1,484121 |
21,20173 |
65,0748 |
|
1,072478 |
15,32112 |
80,3959 |
|
0,738453 |
10,54932 |
90,9453 |
|
0,373828 |
5,34040 |
96,2857 |
|
0,172748 |
2,46783 |
98,7535 |
|
0,087256 |
1,24652 |
100,0000 |
Согласно критерию Кайзера значимыми являются три фактора (с собственными числами больше 1), они суммарно объясняют чуть более 80% всей дисперсии.
Для того чтобы воспользоваться критерием Кеттеля, необходимо изобразить собственные числа в системе координат (рис.1). По оси ОХ располагаем порядковый номер собственного числа, а по оси ОY – значения собственных чисел.
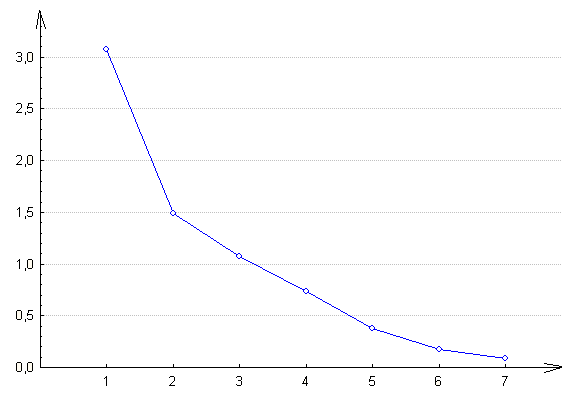
Рис.1. Графическое представление собственных чисел.
Согласно графику факторной осыпью можно считать собственные числа, начиная с пятого, так как именно с этой точки график начинает плавно приближаться к оси ОХ. Причем четыре оставшихся собственных числа объясняют всю дисперсию на 90,9 %. Итак, оптимальное количество факторов данной задачи 3 или 4, более точный результат можно получить путем возможности интерпретации факторов.
Коэффициентами матрицы факторных нагрузок являются нормированные собственные векторы корреляционной матрицы, соответствующие выделенным раннее собственным числам.
Собственные векторы определяются путем решения систем линейных однородных уравнений вида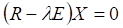 
, а их нормирование производится по формуле 
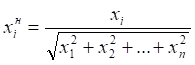. Кроме того, после нормирования каждую координату вектора необходимо умножить на весовой коэффициент, в качестве которого выступает 
.
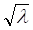Располагая координаты полученных собственных векторов для найденных четырех первых собственных чисел по столбцам, а данные переменные по строке получим матрицу факторных нагрузок (табл.4).
Таблица 4. Факторные нагрузки.
|
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор 4 |
|
|
Рост |
-0,55 |
-0,24 |
0,74 |
-0,19 |
|
Вес |
-0,44 |
0,23 |
0,12 |
0,07 |
|
Память |
0,91 |
0,23 |
0,03 |
0,25 |
|
Логическое мышление |
0,84 |
-0,20 |
0,22 |
0,08 |
|
Техника чтения |
0,36 |
0,52 |
-0,38 |
-0,67 |
|
Фантазия |
-0,50 |
0,63 |
-0,41 |
0,37 |
|
Прыжки в длину |
0,39 |
-0,36 |
-0,80 |
0,22 |
В матрице факторных нагрузок содержатся коэффициенты корреляции между выделенными факторами и исходными переменными, анализ которых показывает, что первый фактор сильнее всего зависит от тестов на память и логическое мышление, т.е. может отвечать за математические способности школьников; второй фактор – гуманитарной направленности; третий – спортивной, а четвертый фактор не поддается интерпретации. В связи с этим в матрице факторных нагрузок оставляем три фактора, а четвертый отбрасываем.
Для нахождения матрицы факторных весов достаточно найти произведение матриц. Элементы матрицы факторных весов (табл.5) являются значениями выделенных факторов для каждого испытуемого.
Таблица 5. Матрица факторных весов.
| математический | гуманитарный | спортивный | |
| И.П. | -0,74 | -0,94 | -1,45 |
| К.Р. | 1,31 | -0,70 | 1,02 |
| М.Ш. | -1,03 | 1,44 | 1,60 |
| Д.Е. | 0,26 | 0,90 | -1,09 |
| Ю.Г. | 0,27 | 0,70 | -0,38 |
| Т.Р. | 1,79 | 0,28 | -0,15 |
| К.Л. | -0,80 | -1,19 | 0,55 |
| О.М. | -0,29 | -1,15 | 0,52 |
| П.Н. | -0,78 | 0,66 | -0,61 |
Анализируя матрицу можно сказать, что все выделенные способности у И.П. ниже среднего (факторные весы <0), но преобладают математические.
В математический класс целесообразно направить К.Р. и Т.Р.; в гуманитарный – Д.Е., Ю.Г., П.Н.; а в спортивный – М.Ш., К.Л., О.М.
Благодаря факторному анализу исходные признаки подвергаются некоторому преобразованию, которое обеспечивает минимальную потерю информации и обеспечивает снижение размерности признакового пространства. Этот метод позволяет, учитывая эффект существенной многомерности данных, лаконично и более просто объяснить многомерные структуры и характер взаимосвязей между ними. Сжатие информации получается за счет того, что число факторов – новых единиц измерения – используется значительно меньше, чем было исходных признаков.
Список литературы / References
1. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы: Учебник. – М.: Финансы и статистика, 2005.– 352с.
2. Куликов, Е. И. Прикладной статистический анализ: учеб. пособие: рек. УМО/ Е.И. Куликов. – 2-е изд., перераб. и доп.. – М.: Горячая линия –Телеком, 2008. - 463 с.
3. Добреньков, В. И. Методы социологического исследования: учеб.: доп. Мин. обр. РФ/ В.И. Добреньков, А.И. Кравченко. – М.: ИНФРА-М, 2009.– 768 с.