НОВАЯ МОДЕЛЬ ТЕПЛОПЕРЕНОСА – ТРАНСЦИЛЛЯТОР БЕГУЩЕЙ ВОЛНЫ
НОВАЯ МОДЕЛЬ ТЕПЛОПЕРЕНОСА – ТРАНСЦИЛЛЯТОР БЕГУЩЕЙ ВОЛНЫ
Научная статья
Филиппов А. И.1, Мухаметзянов Э.В.2, Леонтьев А.3, Садриев А.Ф.4
1, 2,3,4 Стерлитамакский филиал Башкирского Государственного Университета, Стерлитамак, Россия
Аннотация
Описан новый подход к описанию явлений переноса, основанный на использовании свойств трансциллятора бегущей волны. Показано, что коэффициент трансцилляторного переноса инвариантен по отношению к знаку пространственного параметра – амплитуды колебаний А, что, в сравнении с известными моделями, более физично отражает необратимость процесса – неотъемлемое свойство молекулярных процессов переноса.
Ключевые слова: трансциляторный перенос теплоты, монохроматическая волна, число Маха, акустические поля.
Key words: transcillatory heat transfer, monochromatic wave, Mach number, acoustic fields.
Экспериментально установлено [1], что при воздействии волновых полей в сложных средах возрастают значения коэффициентов переноса. Физический механизм этого явления достаточно сложен, и до настоящего времени нет полной теории этого явления. Одним из механизмов, объясняющих явление возрастания коэффициентов переноса, является так называемый трансциляторный [2 ‑ 4] механизм. Его суть состоит в увеличении потока за счет относительного смещения частиц среды, вызываемого волновым полем. Трансциляторный теплоперенос относится к диффузионно-конвективным процессам, возникающим при колебательном относительном перемещении участков или частей среды [5]. Для изучения таких процессов переноса удобно использовать модель трансциллятора бегущей волны. Трансциллятор бегущей волны в наиболее простом случае – это просто область среды, в которой присутствует поперечная бегущая упругая плоская монохроматическая волна. При наложении градиента температуры в такой среде инициируется новый вид переноса тепла – трансцилляторный.
Как и теплопроводность, такой процесс описывается коэффициентом трансцилляторного переноса (КТП). Вычисление коэффициента трансцилляторного переноса производится следующим образом. Сначала определяется величина конвективного потока тепла
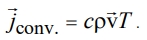 (I)
(I)
Для определения коэффициента трансцилляторного переноса осуществляется осреднение выражения (I) по периоду колебаний и по пространственной ячейке. Несмотря на то, что среднее значение скорости при колебательном движении равно нулю 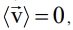 среднее значение конвективного потока, вообще говоря, не равно нулю
среднее значение конвективного потока, вообще говоря, не равно нулю 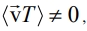 поскольку температурное поле T зависит от скорости
поскольку температурное поле T зависит от скорости 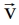 , т.е. они коррелированны. Для определения коэффициента трансцилляторного переноса
, т.е. они коррелированны. Для определения коэффициента трансцилляторного переноса 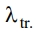 необходимо величину усредненного конвективного потока тепла
необходимо величину усредненного конвективного потока тепла 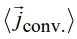 привести к виду, аналогичному закону теплопроводности Фурье
привести к виду, аналогичному закону теплопроводности Фурье
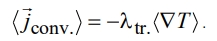 (II)
(II)
Теория явления трансцилляторного переноса приводит к уравнениям в частных производных второго порядка с переменными коэффициентами, аналитическое решение которых сильно затруднено. Поэтому авторами разработан метод редукции к эквивалентному интегральному уравнению, который в большинстве случаев позволяет избежать необходимости построения точного аналитического решения таких уравнений.
Рассмотрим простейший случай однородной среды, находящейся под воздействием плоской поперечной монохроматической волны. Уравнение, описывающее эволюцию температуры T в однородной изотропной среде, имеет вид
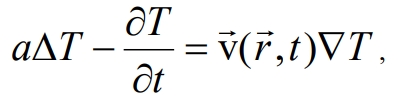 (1)
(1)
где a ‑ коэффициент диффузии; 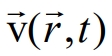 ‑ поле скоростей в волновой зоне. Это уравнение учитывает диффузионные и конвективные процессы, возникающие за счет смещений в волновой зоне.
‑ поле скоростей в волновой зоне. Это уравнение учитывает диффузионные и конвективные процессы, возникающие за счет смещений в волновой зоне.
Получение аналитических решений уравнения (1) для волновых полей затруднено вследствие сложной зависимости скорости колебательного движения от координат и времени. Ниже, в отличие от работы [1], для решения уравнения (1) использован метод редукции к эквивалентному интегральному уравнению, не требующий построения точного аналитического решения. Для простоты полагаем, что волна является поперечной и распространяется вдоль оси Ox со скоростью 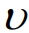 , а отличной от нуля является координата скорости колебаний среды
, а отличной от нуля является координата скорости колебаний среды 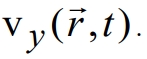
На среду наложено постоянное температурное с градиентом – Гy, направленным против оси у, т.е. градиент температуры совпадает с направлением смещения колеблющихся частиц среды. В соответствии с этим начальное температурное поле представляется в виде 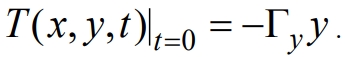 Составляющую градиента скалярного поля – Гy полагаем постоянной. Построение модели теплового трансциллятора бегущей волны при этих предположениях сводится к отысканию решений вида
Составляющую градиента скалярного поля – Гy полагаем постоянной. Построение модели теплового трансциллятора бегущей волны при этих предположениях сводится к отысканию решений вида
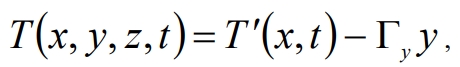 (2)
(2)
Рассмотрим случай монохроматической волны. Для плоской упругой поперечной волны, распространяющейся вдоль оси с плоскостью колебаний, параллельной оси Ox, имеем
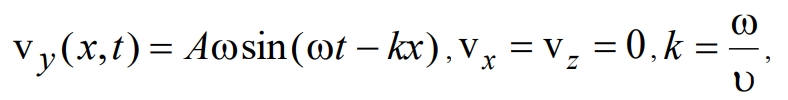 (3)
(3)
где ω ‑ частота колебаний.
Для соответствующего уравнения относительно T'(x,t)
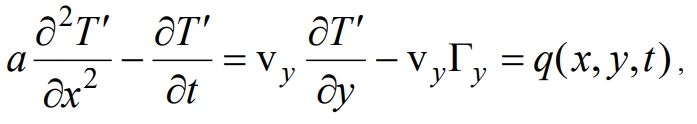 (4)
(4)
где q(x,y,t) ‑ эквивалентный источник теплоты, с однородным начальным условием
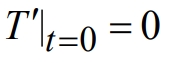 (5)
(5)
с использованием представления T' обобщенной функцией
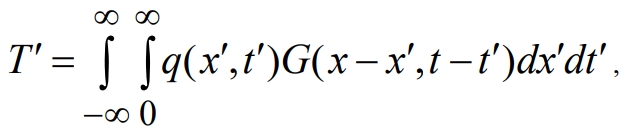 (6)
(6)
получим уравнение для функции Грина
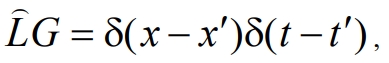 (7)
(7)
где 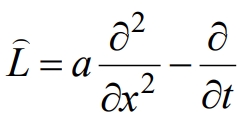 ‑ одномерный оператор теплопроводности.
‑ одномерный оператор теплопроводности.
Для нахождения функции Грина воспользуемся представлением ẟ-функции Дирака в виде
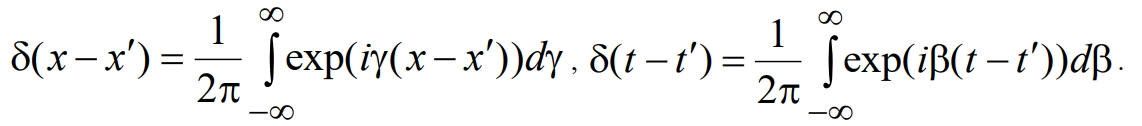 (8)
(8)
С помощью процедуры "деления на оператор" имеем
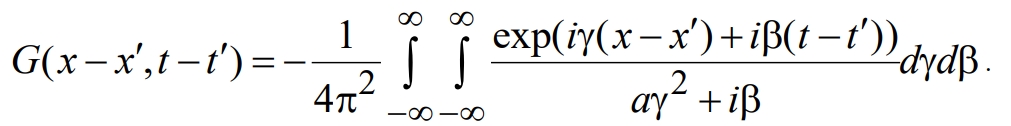 (9)
(9)
Вычислив интегралы в выражении (9), получим
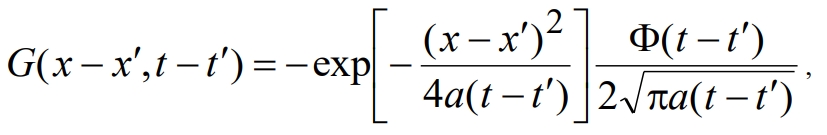 (10)
(10)
где Ф(x) ‑ единичная функция Хевисайда.
С использованием соотношений (6), (4) и (10) запишем эквивалентное исходной задаче интегро-дифференциальное уравнение
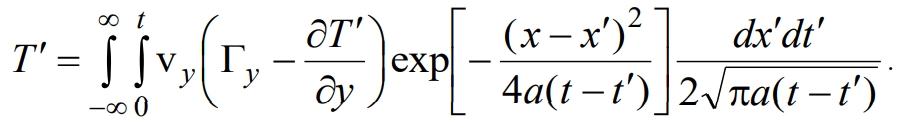 (11)
(11)
Учитывая, что 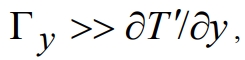 подставляя выражение (3) в (11) и используя формулы Эйлера, после упрощения получаем
подставляя выражение (3) в (11) и используя формулы Эйлера, после упрощения получаем
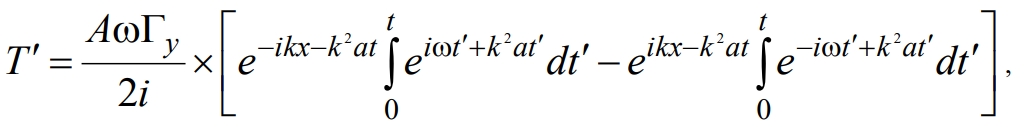 (12)
(12)
и в окончательном виде
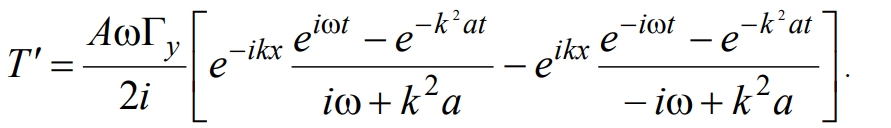 (13)
(13)
Для достаточно больших времен 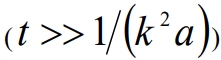 из (13) следует
из (13) следует
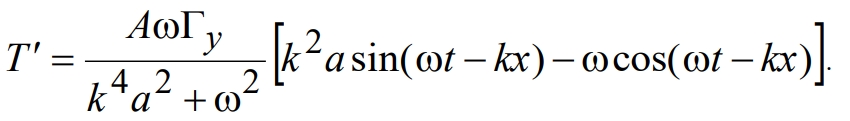 (14)
(14)
Поток теплоты вдоль оси Oy складывается из диффузионного и конвективного потоков:
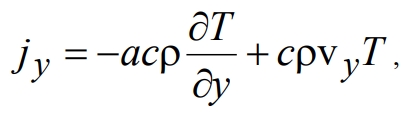 (15)
(15)
где 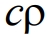 ‑ объемная теплоемкость среды. Рассмотрим конвективную составляющую потока, в которой опущены слагаемые, не вносящие вклада в результаты осреднения, осуществленного ниже
‑ объемная теплоемкость среды. Рассмотрим конвективную составляющую потока, в которой опущены слагаемые, не вносящие вклада в результаты осреднения, осуществленного ниже
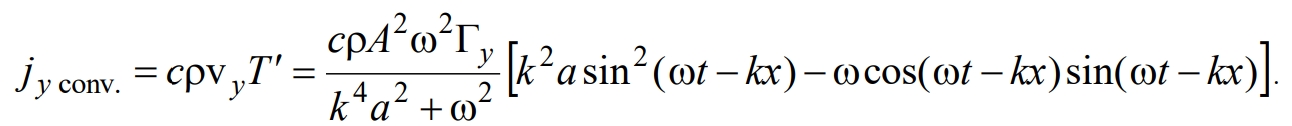 (16)
(16)
Усреднение выражения (16) по периоду колебаний приводит к следующему выражению:
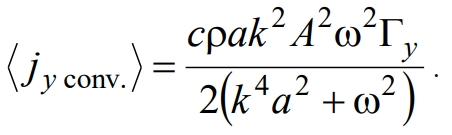 (17)
(17)
Соответствующий коэффициент переноса
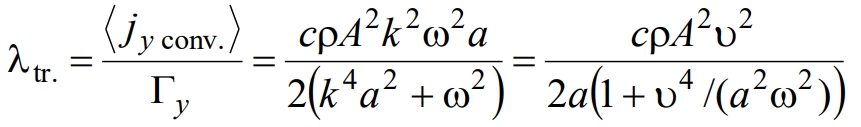 (18)
(18)
называется коэффициентом трансцилляторного переноса. Трансцилляторный перенос теплоты возникает за счет диффузного обмена между слоями среды, участвующими в колебательном движении. Он отличается от чисто конвективного, поскольку регулярного переноса частиц среды в этом случае нет.
Разложим (18) в степенной ряд и, удерживая два члена, получим
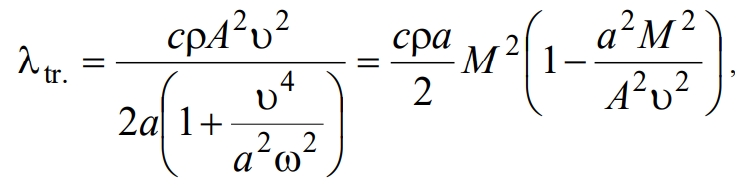
где 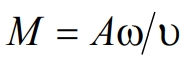 ‑ число Маха.
‑ число Маха.
Результирующий коэффициент переноса вдоль оси Oy представляется в виде суммы диффузного и трансцилляторного коэффициентов:
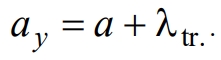
Из (18) следует, что величина коэффициента переноса 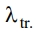 в трансцилляторе бегущей волны пропорциональна квадрату амплитуды колебаний. Это означает, что величина
в трансцилляторе бегущей волны пропорциональна квадрату амплитуды колебаний. Это означает, что величина 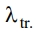 инвариантна по отношению к знаку пространственного параметра – амплитуды колебаний А. Этот факт является прямым указанием на необратимость процесса, что, согласно существующим представлениям, соответствует природе теплопроводности.
инвариантна по отношению к знаку пространственного параметра – амплитуды колебаний А. Этот факт является прямым указанием на необратимость процесса, что, согласно существующим представлениям, соответствует природе теплопроводности.
Это обстоятельство оттеняет преимущества развитого нами подхода, поскольку все известные методы в физике приводят к неинвариантным соотношениям по отношению к знаку пространственного параметра. Например, что коэффициент теплопроводности газа, согласно молекулярно-кинетической теории, пропорционален первой степени средней длины свободного пробега, т.е. не инвариантен по отношению к ее знаку. Это находится в серьезном противоречии с необратимостью процессов теплопроводности, согласно которой, каком бы направлении молекула не двигалась, процесс переноса тепла все равно будет происходить от более нагретых частей к менее нагретым.
Видимо, указанное обстоятельство делает необходимым уточнение классической теории переноса. Это легко осуществимо с помощью развитых в данной статье представлений. Действительно, движение молекул всегда можно представить в виде двух взаимопроникающих сред, движущихся навстречу, т.к. центр масс системы не подвижен. Поскольку при этом молекулы разных сред взаимодействуют, то такая система, конечно, может быть описана в рамках трансцилляторной модели. Проблема при этом сводится только к уточнению содержания констант. Это означает, что мы можем стать свидетелями еще одной увлекательной ревизии фундаментальных разделов физической кинетики.
Список литературы / References
- Филиппов А. И., Филиппов К. А. О диффузии под воздействием звука // Акустический журнал. – 1991. – Т. – № 3. – C. 414 – 417.
- Н е с и с Е. И., Шаталов А. Ф., Кармацкий Н. П. Зависимость коэффициента теплоотдачи от амплитуды и частоты вибрации вертикального тонкого нагревателя // Инженерно-физический журнал. – 1994. – Т. 67, № 1– – C. 20 – 22.
- Нигматулин Р. И., Филиппов А. И., Ахатов И. Ш., Ниязгулов C. А. Уравнения с периодическими коэффициентами и теория хаоса // Статика и динамика упорядоченных сред: Межвузовск. научн. сб. Башк. ун-т. – Уфа. – 1994. – C. 81–93.
- Филиппов А. И., Котельников В. А., Минлибаев М. Р. Некоторые особенности явления переноса тепла при колебаниях в пористой среде // Теплофизика высоких температур. – 1996. – Т. 34, № 65. – С. 708–713.
- ,OliemansR. A turbulent diffusion model for particle dispersion and deposition in horizontal tube flow // Int. J. Multiphase Flow. – 1998. – V. 24, № 1. – P. 55 – 75.
- Gavignet, Ballandars S., Bigler E. Analysis and experimental study of surface transverse wave resonators on quartz // J. Appl. Phys. – 1996. –V. 79(12). – Pp. 8944–8950.
