On one method of discretisation of the Fisher-Kolmogorov-Petrovsky-Piskunov problem

Базовой математической моделью среды, для которой характерна пространственно-временная самоорганизация, выступает нелинейное уравнение реакции-диффузии (УРД): где  — диагональная матрица коэффициентов диффузии,  — неизвестная векторная функция,  — непрерывная и достаточное число раз дифференцируемая функция.

В 1937г. Р. Фишер

(1)

Уравнение Фишера-Колмогорова-Петровского-Пискунова (Ф-КПП) (1) играет большую роль в исследовании биологических, химических и социальных процессов. Справедливости ради, стоит отметить, что первоначально уравнение было предложено Г. Хотеллингом в 1921 г.

В статье

Одним из методов получения априорных оценок для решений разностных схем, а также исследования устойчивости является принцип максимума. Принцип максимума дает только достаточные условия устойчивости, то есть из их невыполнения не следует, что схема неустойчива.  Из априорных оценок в сеточных нормах следует устойчивость решения разностной схемы по отношению к малым возмущениям входных данных задачи. В нелинейном случае из полученных априорных оценок не следует ни единственность сеточного решения, ни устойчивость. Для того чтобы пользоваться доказательным аппаратом принципа максимума, требуется построение разностной схемы, которая была бы монотонна относительно разности между решением разностной задачи с возмущенными входными данными и решением исходной задачи.

Рассмотрим в прямоугольнике 

начально-краевую задачу для одномерного уравнения Фишера-Колмогорова-Петровского-Пискунова:

(2)

(3)

(4)

Далее будем предполагать неотрицательность входных данных (3)-(4).

Введем равномерную сетку 

 — множество внутренних узлов,  — множество граничных узлов, . Значение сеточной функции  в узле обозначим .

Для аппроксимации рассматриваемой нелинейной задачи применим следующую линейную разностную схему с весами:

(5)

где параметры  .

Начальные и краевые условия аппроксимируем точно

(6)

(7)

Ранее в работе

Используя технику принципа максимума

Пусть в ограниченной области задана сетка , на внутренних узлах которой рассматривается уравнение относительно неизвестной сеточной функции :

(8)

 – заданные сеточные функции.

Выделим в качестве центрального узла тот узел, у которого коэффициент максимален по модулю. Запишем разностную схему (8) в канонической форме 

(9)

Шаблон . Для уравнения (9) в граничных узлах зададим условие Дирихле 

Далее будем полагать, что коэффициенты  уравнения (9) удовлетворяют условиям неотрицательности:

(10)

для любого внутреннего узла  и любой точки из окрестности узла .

Приведем ряд теорем, доказанных в

Пусть

Теорема 1. (принцип максимума)

Пусть  — некоторая сеточная функция, заданная на  и не равная постоянной . Тогда, если , то не может принимать наибольшего положительного (наименьшего отрицательного) значения во внутренних узлах .

Теорема 2. 

Пусть функция , определенная на , неотрицательна на границе и выполнено условие

Тогда неотрицательна для всех :

Если же на , на , то

Следствие 1. 

Пусть выполнены условия (10) и . Тогда однородное уравнение имеет единственное решение , а уравнение  однозначно разрешимо при любых правых частях .

Теорема 3. (теорема сравнения)

Пусть  и  — решения задач

где .

Тогда, если на , на , то на .

Следствие 2.

Для решения однородного уравнения

справедлива оценка

где 

Теорема 4.

Пусть коэффициенты уравнения (9) удовлетворяют условиям:

тогда для решения задачи (9) c нулевым граничным условием справедлива оценка

где 

Таким образом, условия положительности коэффициентов

(11)

гарантируют однозначную разрешимость, монотонность и устойчивость в равномерной норме по отношению к малому возмущению входных данных.

Разностное уравнение (5) можно переписать в виде 

Пусть . Шаблон состоит из узлов:

Тогда

Определим условия, при которых схема принадлежит рассматриваемому классу.

Рассмотрим коэффициент канонической формы :

Покажем, что 

(12)

Если , то ввиду неотрицательности параметров и шага , все выражение отрицательно.

Будем рассматривать случай, когда . Заменим функцию ее минимально возможным значением, чтобы максимизировать , тогда при 

(13)

неравенство (12) истинно.

Нетрудно видеть, что для , коэффициенты  положительны.

Пусть :

Если  , то шаг может принимать любое допустимое значение. Однако ввиду малости шага это условие является неестественным. Если же 

(14)

то в этом случае 

(15)

В рассматриваемой задаче при выполнении условий (14)-(15) имеет место неравенство 

Тогда коэффициент  будет вычисляться по формуле 

Положительность  при выполнении условия (13) следует из того, что выражение отрицательно при выполнении этого же условия.

Пусть  

Теорема 5.  Пусть выполнены условия

(16)

(17)

и разностное решение   неотрицательно на сетке .

Тогда справедлива двусторонняя оценка: 

Доказательство.

Будем следовать методике доказательства, изложенной в работе [10, C. 391-398].

На нулевом слое справедлива следующая оценка 

(18)

По индукции предположим, что оценка (18) верна также и для всех . Неравенство справедливо и для .

Максимум и минимум сеточной функции может достигаться либо на границе, либо во внутренней точке сетки.

Запишем оценку, доказанную в работе [11, P. 186–199]: 

(19)

где

Тогда 

(20)

C учетом (20):

Что и требовалось доказать.

Назовем и допустимыми, если они удовлетворяют ограничениям (16), (17) соответственно. Отметим, что множество допустимых значений  и непусто, если принять во внимание произвольность .

Будем рассматривать равномерную сеточную норму 

Следствие.

Для решения разностной схемы (5)-(7) справедлива априорная оценка

Нижеприведенное определение справедливо разностных схем,  аппроксимирующих как линейные, так и  нелинейные краевые задачи.

Определение 1.  Пусть разностная схема 

(21)

аппроксимирует дифференциальную задачу 

и - решение разностной задачи (22) c возмущенными входными данными  (включая начальные и краевые условия): 

(22)

Тогда разностная схема (21) называется монотонной, если из условий 

следует

Будем рассматривать сеточную функцию , где — решение разностной схемы

(5)-(7), а - решение разностной схемы для задачи с возмущенными входными данными:

(23)

(24)

(25)

Тогда поэлементно вычитая из (23)-(25) уравнения (5)-(7), получим задачу для сеточной функции :

(26)

Здесь коэффициенты для значения параметра положительны:

Коэффициенты и имеют вид:

Выше была доказана положительность этих коэффициентов, содержащих в формуле . Применяя аналогичные рассуждения и для , получаем .

Определим условия при которых , где: 

Рассмотрим множитель, входящий в первое слагаемое последней формулы:

Вариант , при котором шаг может принимать любое допустимое значение, не имеет смысла, поскольку весовой коэффициент удовлетворяет условию .

Для случая считаем, что и

Применим двустороннюю оценку (19) к функции : 

где

Рассмотрим отношение 

(27)

Если выполнена оценка 

(28)

и для всех  справедливо

то из отношения (27) следует 

Следовательно, в соответствии с определением 1 разностная схема (5)-(7) является монотонной.

Исследуем устойчивость разностной схемы. Сеточная функция  может достигать своего максимума либо на границе , либо во внутренней точке. Тогда для случая достижения максимума во внутренней точке из уравнения (26) следует неравенство:

Объединим оценки:

(29)

Неравенство (29) демонстрирует устойчивость разностной схемы (5)–(7) при выполнении условия (28) по отношению к малому возмущению входных данных.

Рассмотрим задачу:

(30)

(31)

Приведем результаты численного эксперимента для начально-краевой задачи (30)-(31), которая была получена из исходной задачи установлением параметров .

Численная реализация метода прогонки производилась на языке Python с весовыми коэффициентами и .

Количество отрезков разбиения по оси  и оси  составляет и соответственно. Результаты расчета сравнивались с точным решением, определенным по формуле [6]:

Графики демонстрируют, что численное решение в моменты времени  совпадают с графиками точного решения, имеющими профиль "бегущей волны".

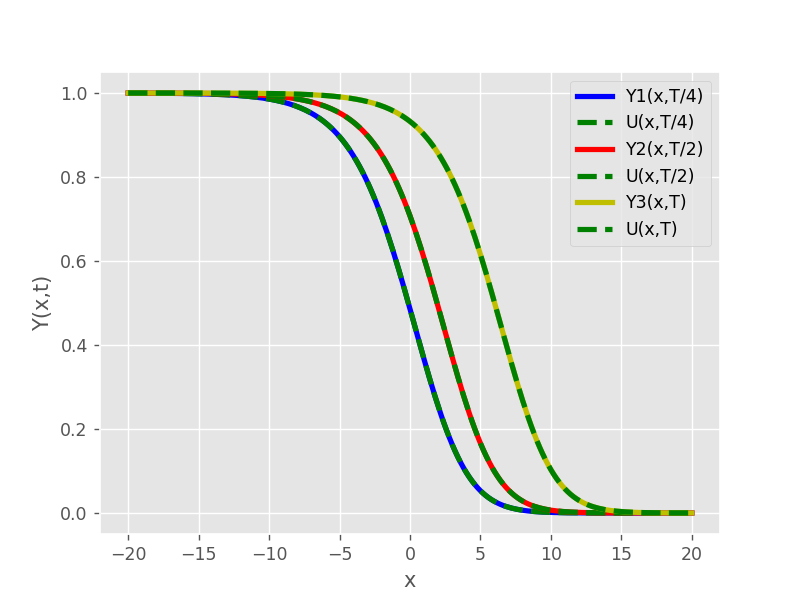
Рисунок 1 - Численное и точное решения в различные моменты времени для M=200, N=400, σ=0,5, β = 0,5.

DOI:10.60797/IRJ.2025.155.92.1

В таблице 1  приведены абсолютные ошибки численного решения на разных временах, полученные при расчете с параметрами . Таблица 2 содержит относительные ошибки численного решения при тех же параметрах.

В данной работе построена и исследована разностная схема для квазилинейного параболического уравнения Ф-КПП. Получены двусторонние оценки разностного решения, доказаны монотонность и достаточное условие устойчивости рассмотренного метода в сеточном аналоге нормы , проведен вычислительный эксперимент. Неизвестно является ли условие устойчивости необходимым условием. Результаты численного моделирования  показывают, что устойчивость имеет место и при нарушении этих условий.