Journals
Submit manuscript Sign in / Sign up
Advanced search
Article sections
Review

INCREASING THE RESISTANCE OF MAGNETIC FLUX CONCENTRATOR DURING GENERATION OF STRONG PULSED MAGNETIC FIELDS

Research article
Russkikh P. A.
Boltachev G. S.
DOI:
https://doi.org/10.60797/IRJ.2025.155.57
Issue: № 5 (155), 2025
Suggested:
11.03.2025
Accepted:
29.04.2025
Published:
16.05.2025
462
9
XML
PDF

Abstract

The possibility of significant increase of generated pulse magnetic fields by the inductor system "one-turn solenoid + concentrator" without reaching the dangerous threshold of low-cycle fatigue mechanism initialisation is theoretically examined by varying the dimensions of the inductor system, the material of the concentrator, and the parameters of the discharge circuit. The analysis is carried out on the basis of self-consistent solution of the equation of dynamics of the discharge electric circuit with equations describing spatial distributions in the inductor and concentrator of magnetic and temperature fields, mechanical stresses and deformations. It is shown that for traditionally used steel concentrators by varying the electrical resistance of the circuit it is possible to increase the amplitude of generated pulsed magnetic fields without the threat of concentrator destruction by about 25%, from 32 Tesla to 40 Tesla.

Keywords:
magnetic field diffusion, thermomechanical stresses, Mises condition.

1. Введение

Перспективным подходом для широкого круга технологических задач является магнитно-импульсная обработка

,
,
,
. В то же время внедрению этого подхода препятствует невысокий ресурс индукторных систем, используемых для генерирования сильных импульсных магнитных полей с амплитудой порядка 30-60 Тл. Низкий ресурс обусловлен разрушением рабочей поверхности — проводника, ограничивающего область магнитного поля
,
,
,
. Под воздействием интенсивных термомеханических напряжений, сопровождающих процесс генерирования импульсных полей, на поверхности проводника появляются трещины, которые достаточно быстро прорастают вглубь за счет эффекта пилы
,
. Зарождение первоначальных трещин на поверхности материала, обладающего некоторым ресурсом пластичности, происходит по механизму малоцикловой усталости
,
. В рамках модели идеального упруго-пластичного тела механизм малоцикловой усталости запускается, если в ходе цикла «нагрев–охлаждение», обусловленного протеканием поверхностных токов, проводящий материал дважды достигает предела текучести: при нагреве и при последующем охлаждении
,
,
,
. Поэтому в данном исследовании, которое является продолжением работ
,
,
, мы в качестве порогового магнитного поля будем подразумевать амплитуду
импульса магнитной индукции, при которой проводящий материал достигает условия пластического течения на стадии остывания.

В литературе для увеличения стойкости проводящей поверхности обсуждались различные подходы

,
,
,
, в частности: создание в материале градиентного профиля удельного сопротивления
,
,
,
, использование диамагнитного экрана с инерционным удержанием
, оптимизация формы генерируемого магнитного импульса
,
. В реальных экспериментальных условиях импульс 
определяется динамикой разрядного контура, и с удовлетворительной точностью может быть представлен в виде затухающей синусоиды
,
,
,
.

(1)

где

 — характерное время затухания,
— период. В наших предшествующих исследованиях
,
было показано, что заметное увеличение порогового поля
может быть достигнуто при уменьшении параметра
или при увеличении периода
. Как отмечается в
, условие
{{\tau }_{s}}>{{\tau }_{e}}
соответствует эффективному «гашению» электрических колебаний, следующих за первой полуволной импульса (1), и приводящих к лишнему («паразитному») нагреву проводника.

В экспериментальных условиях изменение формы импульса генерируемого поля

возможно за счет таких параметров разрядного контура, как его собственное сопротивление
и индуктивность
. С целью теоретического анализа различных возможностей повышения ресурса концентраторов магнитного потока и, в частности, влияния параметров
и
на пороговое поле
представленная в настоящей работе модель учитывает, что индуктор, представляющий собой одновитковый соленоид с размещенным внутри него концентратором, является частью разрядного RLC-контура. Численное моделирование включает самосогласованное решение уравнения динамики контура с дифференциальными уравнениями, описывающими пространственные распределения в соленоиде и концентраторе магнитных и температурных полей, механических напряжений и деформаций. Достижение предела текучести материала определяется на основе критерия текучести Мизеса, а процесс пластического деформирования — в соответствие с ассоциированным законом течения
.

2. Теоретическая модель

Схематичное изображение моделируемой системы «RLC-контур + соленоид + концентратор» представлено на рис. 1. Одновитковый соленоид с внутренним и внешним радиусами

и
, соответственно, имеет длину
, которая совпадает с длиной внешней поверхности концентратора. Усиление магнитного поля концентратором происходит за счет уменьшения его длины
с уменьшением радиуса по линейному закону:

Схематичное изображение моделируемой системы

Рисунок 1 - Схематичное изображение моделируемой системы

DOI:10.60797/IRJ.2025.155.57.1
(2)

где

— длина внутренней (рабочей) поверхности концентратора,
и
— его внутренний и внешний радиусы, соответственно. Поскольку концентратор электрически изолирован, то полный ток через него равен нулю:

(3)

Подставляя выражение (2) для

в интеграл (3), и интегрируя по частям, получим

(4)

где

— сила тока,
 — магнитная постоянная,
и
— магнитные поля на внутренней и внешней границах концентратора. Индукции полей на внутренней границе соленоида и внешней границе концентратора принимались равными. Выражение для
соответствует полю бесконечно длинного соленоида. Чтобы найти силу тока
, воспользуемся тем, что оба проводника являются частью электрической цепи, которая характеризуется собственной индуктивностью
, сопротивлением
и емкостью конденсаторной батареи
(рис. 1). Динамика электрического контура определяется законом Ома:

(5)

где

— время,
— напряжение на конденсаторной батарее,
— ее заряд,
— падение напряжения на соленоиде, для которого имеем

(6)

Здесь

— плотность тока в соленоиде,
— его удельное электрическое сопротивление. Используя соотношение (6) на радиусе
с учётом выражений (4), и подставляя его в выражение (5), приходим к дифференциальному уравнению контура в виде:

{{L}_{eff}}\frac{{{d}^{2}}q}{d{{t}^{2}}}+{{R}_{e}}\frac{dq}{dt}+\frac{q}{C}=\Delta {\varphi }'={{j}_{s,1}}{{\rho }_{s,1}}2\pi {{R}_{s,1}}-\pi R_{1}^{2}\frac{{{L}_{r}}}{{{L}_{1}}}\int\limits_{{{R}_{1}}}^{{{R}_{2}}}{\frac{\partial B}{\partial t}\,dr}+2\pi \int\limits_{{{R}_{1}}}^{{{R}_{2}}}{\frac{\partial B}{\partial t}r\,dr},
(7)

где

\Delta {\varphi }'
— оставшаяся часть разности потенциалов на соленоиде после вычета членов, вошедших в формирование эффективной индуктивности
. Начальные условия к уравнению (7):

(8)

где

— начальное зарядное напряжение.

Численное решение уравнения динамики контура (7) требует в каждый момент времени информации о пространственных распределениях по соленоиду и концентратору магнитного поля

и температуры
, ввиду температурной зависимости удельного сопротивления. Эти распределения находились в одномерной, аксиально-симметричной, постановке, т.е. в пренебрежении краевыми эффектами на торцах индукторной системы
,
. При этом в цилиндрической системе координат
с осью Oz, совпадающей с осью симметрии, магнитное поле
, плотность тока
, вектор перемещений
, и определяющие уравнения — уравнение диффузии магнитного поля и уравнение теплопроводности — принимают вид:

(9)

Здесь в случае концентратора

— удельное сопротивление концентратора, в случае соленоида
,
— теплоемкость на единицу объема,
— коэффициент теплопроводности, а
,
— соответствующие диагональные элементы тензоров напряжений и деформаций, причем

(10)

Для удельного сопротивления принимается линейная зависимость от температуры:

(11)

где

— температурный коэффициент электросопротивления,
— начальное, при температуре
, значение сопротивления.

Начальные и граничные условия для уравнения теплопроводности (9) задавались в виде:

(12)

где

— коэффициент теплоотдачи. Для уравнений диффузии магнитного поля в соленоиде и концентраторе начальные условия были нулевые, т.е.
во всей индукторной системе. Граничные условия для уравнения магнитной диффузии (9) определяются уравнениями (4) и равенством нулю магнитной индукции на внешнем радиусе соленоида, при
.

Механическая задача о пространственном распределении напряжений

, деформаций 
и перемещений
решалась только для концентратора; для соленоида вклад соответствующих членов в уравнение теплопроводности полагался равным нулю. В качестве определяющих уравнений использовались: условие механического равновесия —

(13)

с граничными условиями

,
; линейные соотношения между напряжениями
и упругими деформациями
—

(14)

где

и
— коэффициенты Ламе,
— модуль всестороннего сжатия,
— температурный коэффициент объемного расширения. В области, где материал не выходит за рамки упругих напряжений, т.е.
, перечисленных соотношений (10), (13) и (14) достаточно для однозначного решения механической задачи. Достижение упруго-пластичного предела определялось на основании критерия текучести Мизеса
,
,
:

(15)

где 

— предел текучести материала при одноосном растяжении,
— температура плавления. С достижением предела (15) полная деформация
начинает содержать упругую
и пластическую
части, т.е.
, для однозначного определения которых требуются дополнительные соотношения:

(16)
(17)

которые представляют собой закон ассоциированного течения (16) и условие неизменности объема (17) в процессе пластического течения.

3. результаты и обсуждение

Ниже обсуждаются результаты моделирования в рамках представленной в предыдущем разделе теоретической модели. Система дифференциальных уравнений (7), (9) и (13) решалась численно. Параметры расчета соответствуют экспериментальной установке работ

,
,
:
 мм,
 мм,
 мм,
 мм,
 мм,
 мм и
 мкФ; материал соленоида и концентратора — сталь 30ХГСА с характеристиками:
 Ом∙м,
 кДж/(м3⸱К),
 К–1,
 Вт/(м∙К),
 ГПа,
,
 К–1,
 ГПа,
°С,
 Вт/(м2∙К).

Электрические параметры RLC-контура — собственные индуктивность

и сопротивление
— были определены из условия наилучшего согласия теоретической модели с экспериментальными данными о временных развертках тока в цепи
и магнитного поля во внутренней полости концентратора
. Получено:
 нГн и
 мОм. Достигнутое согласие теории и эксперимента при этих параметрах для зарядных напряжений конденсаторной батареи
 кВ и 10,0 кВ продемонстрировано на рис. 2. Отметим, что для надежного определения параметров
и
нами использовались только первые три полупериода экспериментальных импульсов тока и магнитного поля. После третьего полупериода значения тока и магнитного поля становятся меньше погрешности их экспериментального измерения, поэтому в теоретических расчетах мы полагали
после третьего полупериода.

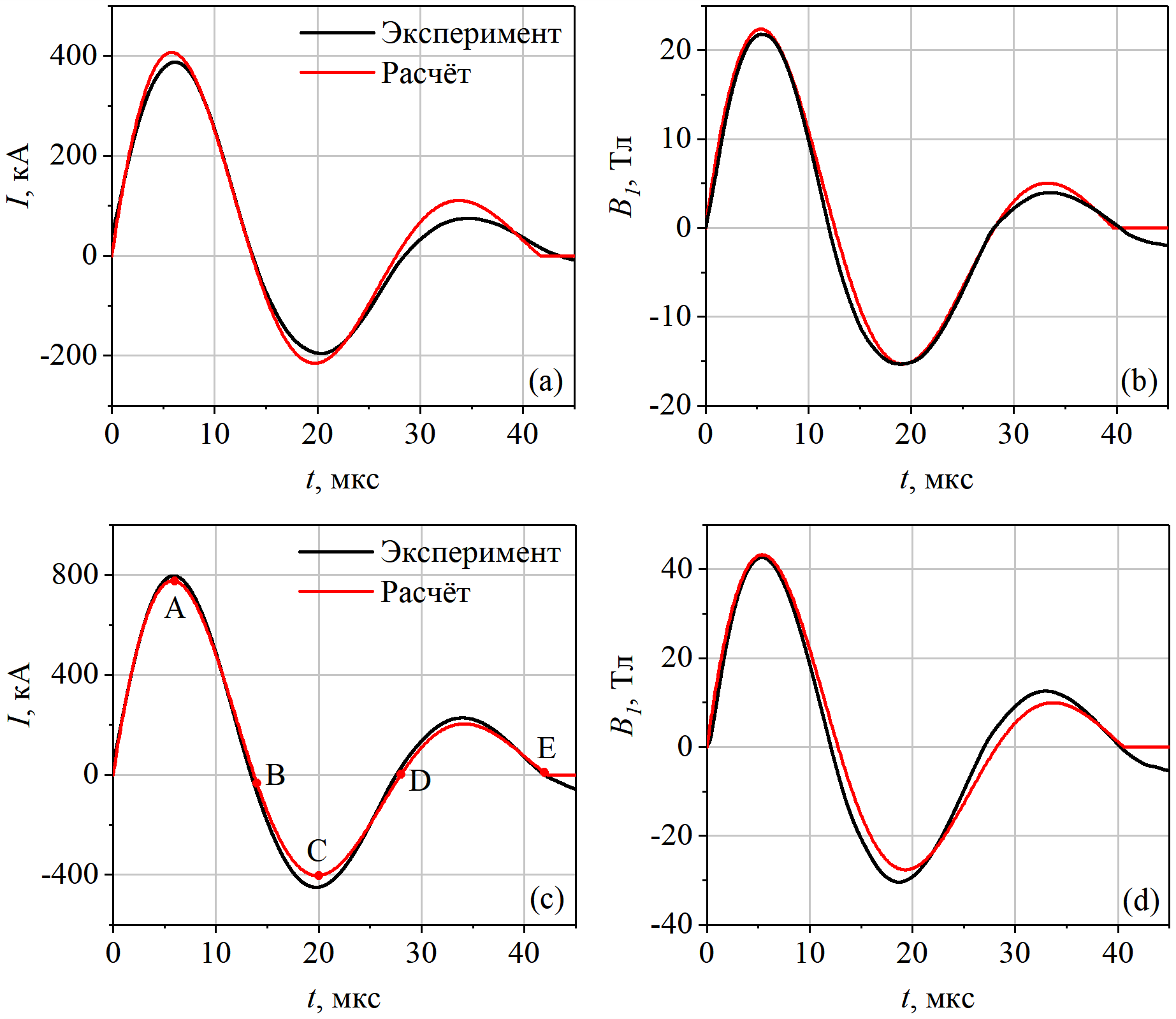
Импульс тока в электрическом контуре I(t) (a,c) и магнитного поля на внутренней поверхности концентратора B1(t) (b,d) при зарядном напряжении U0 = 5,2 кВ (a,b) и 10,0 кВ (c,d)

Рисунок 2 - Импульс тока в электрическом контуре I(t) (a,c) и магнитного поля на внутренней поверхности концентратора B1(t) (b,d) при зарядном напряжении U0 = 5,2 кВ (a,b) и 10,0 кВ (c,d)

DOI:10.60797/IRJ.2025.155.57.2
На рис. 3 показаны расчетные распределения плотности тока по концентратору и соленоиду при зарядном напряжении
 кВ в моменты времени
, 14, 20, 28 и 42 мкс, которые соответствуют точкам A-E на рис. 2. Видно, что максимальные амплитуды плотности тока наблюдаются на внутренней
и внешней
поверхностях концентратора, а также на поверхности соленоида при
, поэтому именно эти поверхности подвергаются максимальному нагреву и, как следствие, максимальным термоупругим напряжениям. С удалением от поверхностей вглубь концентратора и соленоида амплитуды колебаний плотности тока быстро снижаются. Заметим, что для периодического импульса с длительностью
 мкс толщина классического скин-слоя
в стали составляет порядка 1,7 мм.
Распределения плотности тока по концентратору (a) и соленоиду (b) при зарядном напряжении U0=10 кВ в моменты времени, отмеченные на рис. 3: t=6 (линии 1), 14 (2), 20 (3), 28 (4) и 42 мкс (5)

Рисунок 3 - Распределения плотности тока по концентратору (a) и соленоиду (b) при зарядном напряжении U0=10 кВ в моменты времени, отмеченные на рис. 3: t=6 (линии 1), 14 (2), 20 (3), 28 (4) и 42 мкс (5)

DOI:10.60797/IRJ.2025.155.57.3
Температуры максимального нагрева всех трех поверхностей, ограничивающих магнитное поле, при разряде контура с начальным зарядным напряжением
 кВ представлены на рис. 4а. Рисунок показывает, что наиболее высокий уровень нагрева наблюдается на внутренней поверхности концентратора, где к моменту
 мкс приращение температуры составляет
 К. Для сравнения, на его внешней поверхности и на поверхности соленоида максимальный нагрев составляет порядка 362 и 405 К, соответственно. На стадии нагрева хорошо заметны три последовательных участка, соответствующих трем полупериодам импульса тока в разрядном контуре. При этом нагрев к концу первого (основного) полупериода (
 мкс) составляет
 К, т.е. почти вдвое ниже максимального значения. На стадии охлаждения первоначальное снижение температуры всех трех поверхностей (
,
и
) связано, в основном, с оттоком тепла во внутренние менее нагретые слои концентратора и соленоида. Этот процесс выравнивания температуры завершается к
 с, после чего дальнейшее относительно медленное охлаждение обусловлено процессом теплоотдачи поверхностей.
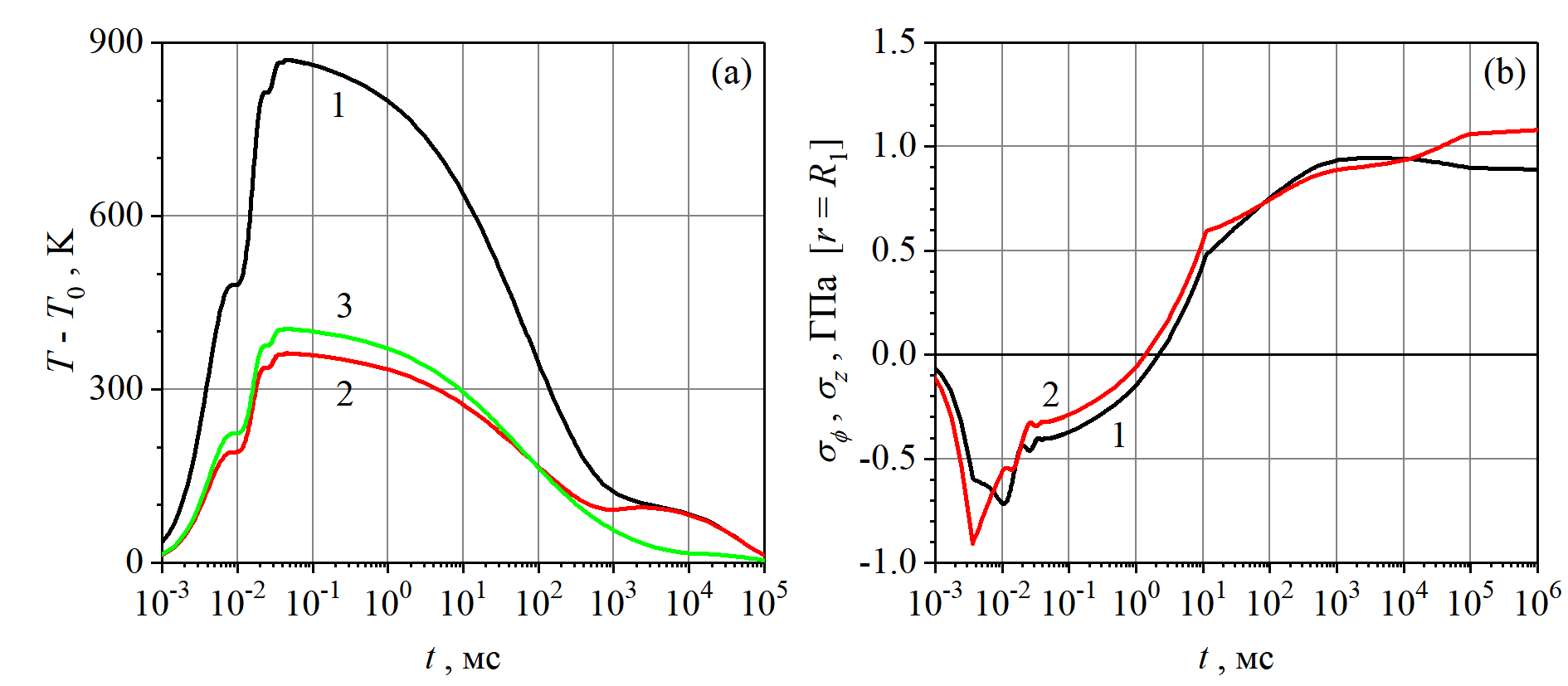
Временные зависимости температуры (a) на поверхностях r = R1 (линия 1), r = R2 (линия 2), r = Rs,1 (линия 3), и компонент тензора напряжения: σφ (линия 1) и σz (линия 2) (b) на поверхности r = R1 при зарядном напряжении U0 = 10 кВ

Рисунок 4 - Временные зависимости температуры (a) на поверхностях r = R1 (линия 1), r = R2 (линия 2), r = Rs,1 (линия 3), и компонент тензора напряжения: σφ (линия 1) и σz (линия 2) (b) на поверхности r = R1 при зарядном напряжении U0 = 10 кВ

DOI:10.60797/IRJ.2025.155.57.4
На рис. 4b показаны азимутальная и аксиальная компоненты тензора напряжений на внутренней поверхности концентратора. Заметим, что радиальная компонента
здесь обращается в ноль согласно граничному условию на свободной поверхности. Рисунок показывает, что нагрев материала в течение разряда приводит к состоянию тангенциального (по отношению к поверхности) сжатия:
{{\sigma }_{i}}<0
(
). Излом на кривых
в момент
 мкс связан с достижением критерия текучести (15) и началом пластического деформирования, которое разгружает избыточное тангенциальное сжатие. Увеличение температуры приводит к снижению предела текучести 
в связи с чем, возвращение материала в упругое состояние, т.е. прекращение пластического течения, происходит только к моменту
 мкс. Накопленная в этом процессе пластическая деформация приводит к необратимости процесса «нагрев-охлаждение». Как результат, полное остывание материала до исходной температуры
не приводит к начальному состоянию, которое характеризуется отсутствием упругих напряжений. Как можно видеть на рис. 4b, при
t>2
 мс снижение температуры приводит к появлению положительных азимутальных и аксиальных напряжений на поверхности, т.е. материал переводится в состояние тангенциального растяжения. Повторное достижение предела текучести в момент
 мкс, которое опять проявляется в виде излома на кривых
, гарантирует появление пластической деформации при последующих аналогичных разрядах конденсаторной батареи, т.е. инициирование механизма малоцикловой усталости.

Таким образом, максимальная амплитуда магнитного поля

 Тл, соответствующая разряду с
 кВ, превышает пороговое значение
. Снижение зарядного напряжения и, соответственно, амплитуды магнитного поля приводит к сдвигу момента появления второго излома на рис. 4b в область больших времен и, наконец, к исчезновению, которое происходит при зарядном напряжении
 кВ со значением
 Тл. Проанализируем, как можно повысить пороговое значение
, варьируя различные параметры индукторной системы. В первую очередь, посмотрим, что дает изменение радиальных размеров концентратора.

На рис. 5a представлены расчетные пороговые поля

, которые характеризуют магнитные поля во внутренней полости концентратора, и амплитуды поля, генерируемого при этом соленоидом
, в зависимости от внутреннего радиуса концентратора
. Влияние
проанализировано для условий, когда пропорционально увеличиваются все радиальные размеры индукторной системы, т.е.
, где
, «s,1» и «s,2», и для условий, когда остальные размеры зафиксированы, т.е.
. В частности, при пропорциональном увеличении всех размеров до
 мм пороговое поле
 Тл (это значение отмечено горизонтальной пунктирной прямой) соответствует предельному значению магнитного поля, которое используемый соленоид может выдержать без концентратора. Вставка используемого концентратора (
 мм,
 мм) незначительно повышает достигаемое поле (
 Тл), но зато существенно снижает воздействие на соленоид: поле на его поверхности понижается до величины
 Тл. Резкий рост порогового поля при
{{R}_{1}}>10
 мм для условий
обусловлен «вырождением» концентратора: с уменьшением его толщины, при
, во-первых, исчезает различие между полями
и
, а, во-вторых, поле начинает пронизывать концентратор насквозь, не индуцируя в нем тока. При этом концентратор перестает подвергаться разрушительным термонапряжениям, но и перестает защищать соленоид, поле на поверхности которого при
 мм достигает порогового значения
 Тл. Наиболее оптимальными значениями внутреннего радиуса концентратора, обеспечивающими максимальные значения порогового поля, являются
 мм (т.е.
) при фиксировании всех других радиусов (
) и
 мм (т.е.
) при
. Пороговые поля, реализуемые при этом:
и 32,8 Тл, соответственно. Однако их реализация потребует заметного увеличения зарядного напряжения (см. рис. 5b), до значения
 кВ.

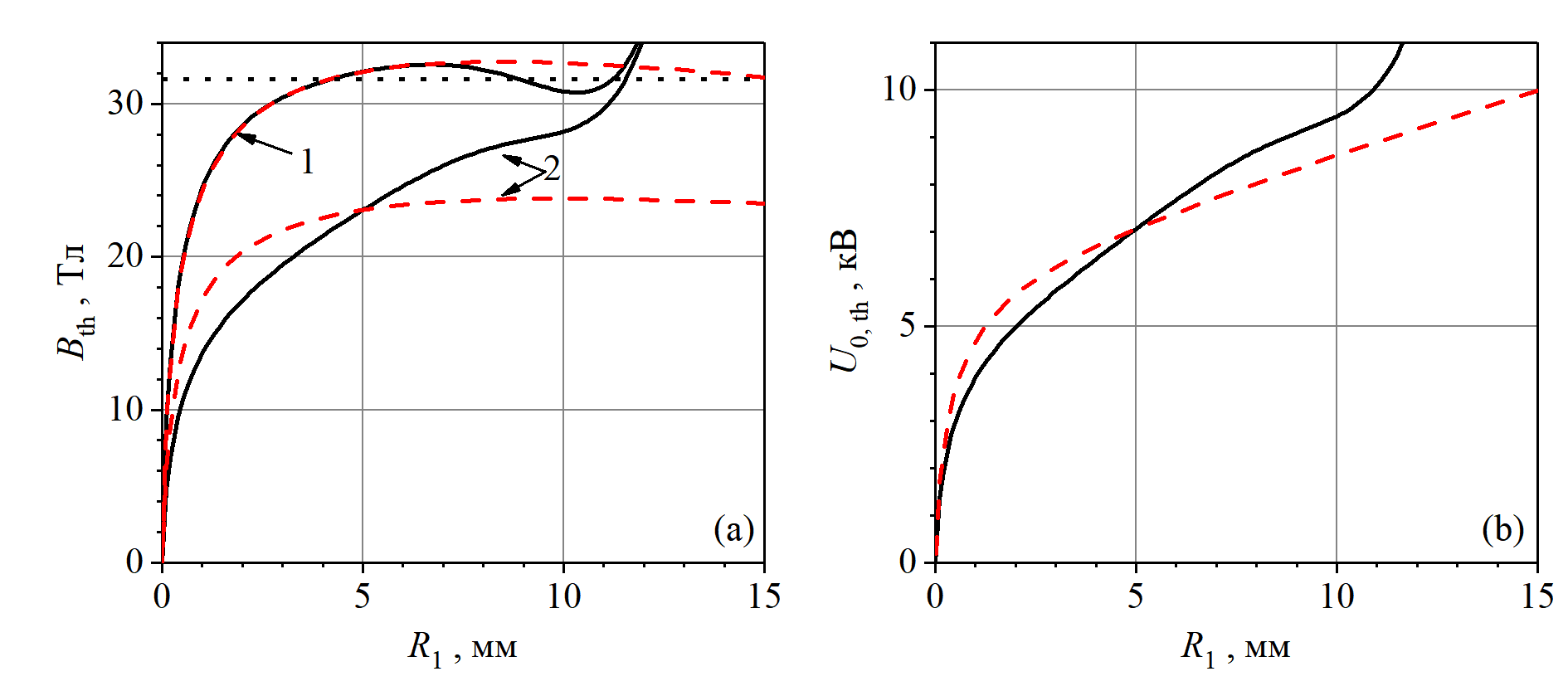
Пороговые поля Bth (линии 1), соответствующие поля соленоида B2,max (линии 2) (a), и – зарядные напряжения в зависимости от внутреннего радиуса концентратора R1 (b)

Рисунок 5 - Пороговые поля Bth (линии 1), соответствующие поля соленоида B2,max (линии 2) (a), и – зарядные напряжения в зависимости от внутреннего радиуса концентратора R1 (b)

Примечание: штриховые красные линии - при пропорциональном увеличении всех радиальных размеров индукторной системы, т.е. при условии Ri - R1=const; сплошные черные линии — при Ri = const (i = 2, «s,1», «s,2»)

DOI:10.60797/IRJ.2025.155.57.5
Другим гипотетически возможным способом повлиять на пороговое поле
является варьирование удельного сопротивления материала концентратора
. Проанализируем влияние
на поле
, полагая все остальные параметры системы, включая прочностные характеристики концентратора, температурный коэффициент сопротивления
и т.д., неизменными. Зависимость
представлена на рис. 6. При уменьшении
от значения, соответствующего используемой стали
 Ом∙м, пороговое поле возрастает, вплоть до величины
 Тл в гипотетическом пределе
, что составляет примерно 25%. Наличие конечного предела
обусловлено тем, что при
весь протекающий по проводящему материалу ток концентрируется в поверхностном слое с толщиной порядка толщины скин-слоя
. Таким образом, при определенной величине поверхностного тока мы имеем вполне определенное значение плотности тепловыделения:
(18)

независящее от удельного сопротивления. Поэтому достижения нагрева

, приводящего к появлению пороговых термонапряжений, определяется только импульсом магнитного поля
, и, в частности, его амплитудой.

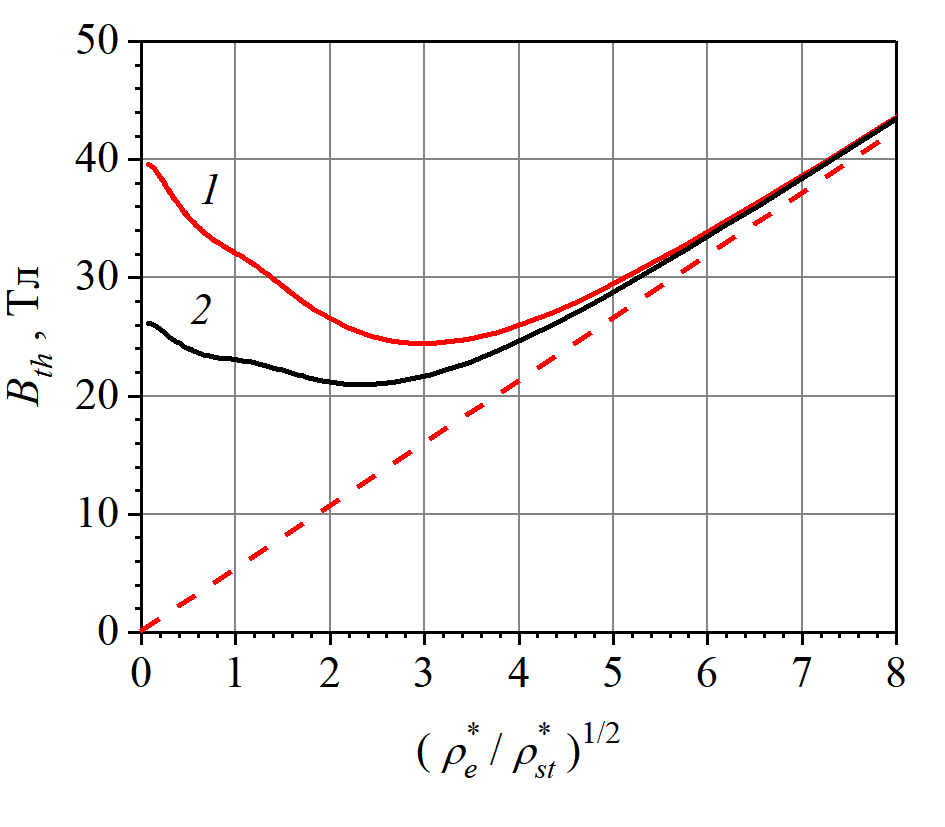
Зависимость порогового поля (линия 1, Bth) и поля соленоида (линия 2, B2,max) от удельного сопротивления материала концентратора. Штриховая линия показывает асимптотику Bth2~ρe* 

Рисунок 6 - Зависимость порогового поля (линия 1, Bth) и поля соленоида (линия 2, B2,max) от удельного сопротивления материала концентратора. Штриховая линия показывает асимптотику Bth2~ρe* 

DOI:10.60797/IRJ.2025.155.57.6
На противоположном пределе, при
, достижение определенного тепловыделения требует снижения поверхностной плотности тока
, что согласно уравнению диффузии (9) дает
. Как показывает рис. 6, рост удельного сопротивления от значения
вначале снижает пороговое поле. При
зависимость
проходит через минимум. Затем, при дальнейшем увеличении сопротивления, пороговое поле возрастает, в пределе выходя на асимптотику
. Однако этот рост «стойкости» концентратора также как и на рис. 5 связан с его «вырождением»: одновременно с ростом поля
, которое выдерживает концентратор, поле на поверхности соленоида также нарастает и достигает порогового значения в 31.6 Тл при
.

Перспективным способом более ощутимо повысить пороговое поле индукторной системы, как показывает теоретический анализ, выполненный в работах

,
, является оптимизация формы генерируемого магнитного импульса
. Повышению
способствует эффективное «гашение» электрических колебаний, следующих за первой полуволной импульса, см. рис. 1, и приводящих к лишнему («паразитному») нагреву проводника. Изменение формы импульса генерируемого поля возможно за счет варьирования таких параметров разрядного контура, как его собственное сопротивление
и индуктивность
. Если снижение этих параметров обеспечить в используемой экспериментальной установке затруднительно, то их увеличение не составляет принципиальной проблемы. Для анализа влияния параметров
и
на величину порогового поля
мы оценили изменение
вдоль зависимостей
, определяемых соотношением

${{L}_{e}}({{R}_{e}})={{L}_{e,0}}+\alpha \frac{{{L}_{e,0}}}{{{R}_{e,0}}}({{R}_{e}}-{{R}_{e,0}}),
(19)

где

— коэффициент пропорциональности. При
рост сопротивления
не связан с изменением индуктивности, т.е.
. Полученные зависимости
при значениях
, 0.5, 1.0 и 1.5 представлены на рис. 7a. Видим, что увеличение сопротивления RLC-контура может существенно повысить значения порогового поля, особенно если это не сопровождается ростом его индуктивности. Так, при
увеличение сопротивления до значения
позволяет повысить
на 26%, c 32,1 Tл до 40,3 Tл. При этом требуемое зарядное напряжение повышается с
 кВ до 18.8 кВ, что связано с заметным ростом омических потерь в индукторной системе, а импульс тока приобретает классический апериодический вид (см. рис. 7b).

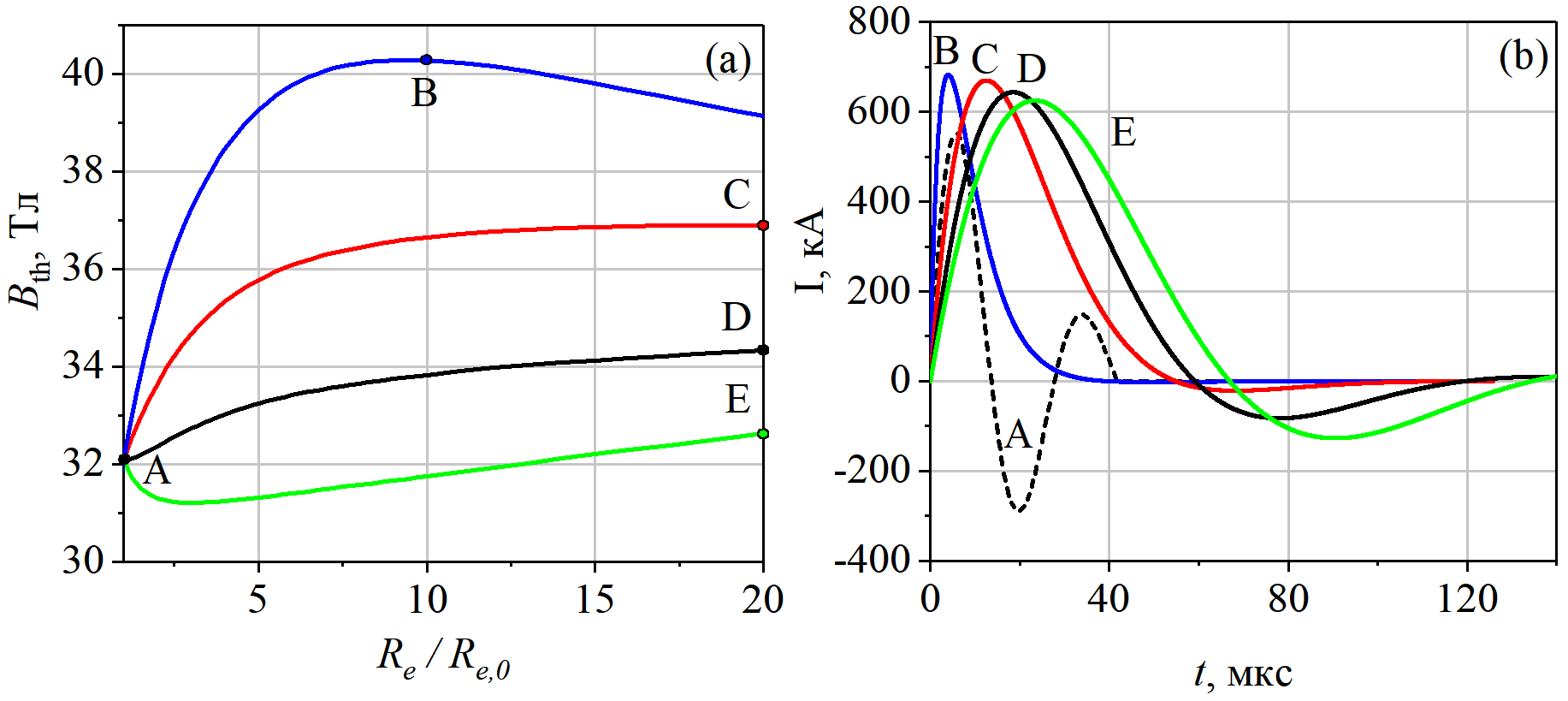
Зависимость порогового поля Bth (a) от сопротивления электрического контура Re вдоль зависимостей Le(Re), определяемых ур. (19) с параметром α =0, 0.5, 1.0, 1.5 и временные развертки тока при разряде RLC-контура, соответствующие точкам A-E (b)

Рисунок 7 - Зависимость порогового поля Bth (a) от сопротивления электрического контура Re вдоль зависимостей Le(Re), определяемых ур. (19) с параметром α =0, 0.5, 1.0, 1.5 и временные развертки тока при разряде RLC-контура, соответствующие точкам A-E (b)

DOI:10.60797/IRJ.2025.155.57.7
Как показывают проведенные численные оценки, вдоль кривой с
на рис. 7a зависимость
также проходит через максимум при
, который, однако же, располагается при значительно меньшем значении,
 Тл, чем максимум на кривой с
. Пороговые поля
при
и 1,5 вплоть до значений
имеют еще меньшие значения. Рис. 7b показывает, что на этих кривых, несмотря на рост сопротивления, не реализуется апериодический режим электрических колебаний, что, в свою очередь, не позволяет эффективно погасить «лишний» нагрев проводящего материала на стадии снижения магнитного поля. Отметим также, что величина зарядного напряжения, требуемого для генерирования магнитного поля с пороговой амплитудой
при сопротивлении
, составляет
 кВ (
), 44,9 кВ (1,0) и 48,1 кВ (1,5). Это существенно превышает возможности, используемой в экспериментальных работах
,
,
,
конденсаторной батареи, максимальное зарядное напряжение которой составляет порядка 25 кВ.

Наконец, в заключение проанализируем возможность одновременного использования высокого значения сопротивления контура

и поверхностной модификации материала концентратора, которая была подробно исследована в работах
,
,
. Для модифицированного материала концентратора удельное сопротивление вместо ур. (11) задается соотношениями

(20)

где функция

описывает начальный пространственный профиль сопротивления вблизи рабочей поверхности концентратора;
— «амплитуда» профиля,
— его характерная глубина. Показатель
определяет характер начального профиля: при 
мы имеем достаточно плавное, экспоненциальное изменение удельного сопротивления, а с увеличением
зависимости
приобретают более резкий, «пороговый» характер. В соответствие с анализом, проведенным в работах
,
,
, ограничим наше рассмотрение модификациями с относительно небольшой амплитудой,
, которая может быть осуществлена на практике, например, методами ионно-плазменной обработки
,
или диффузионного хромирования
.

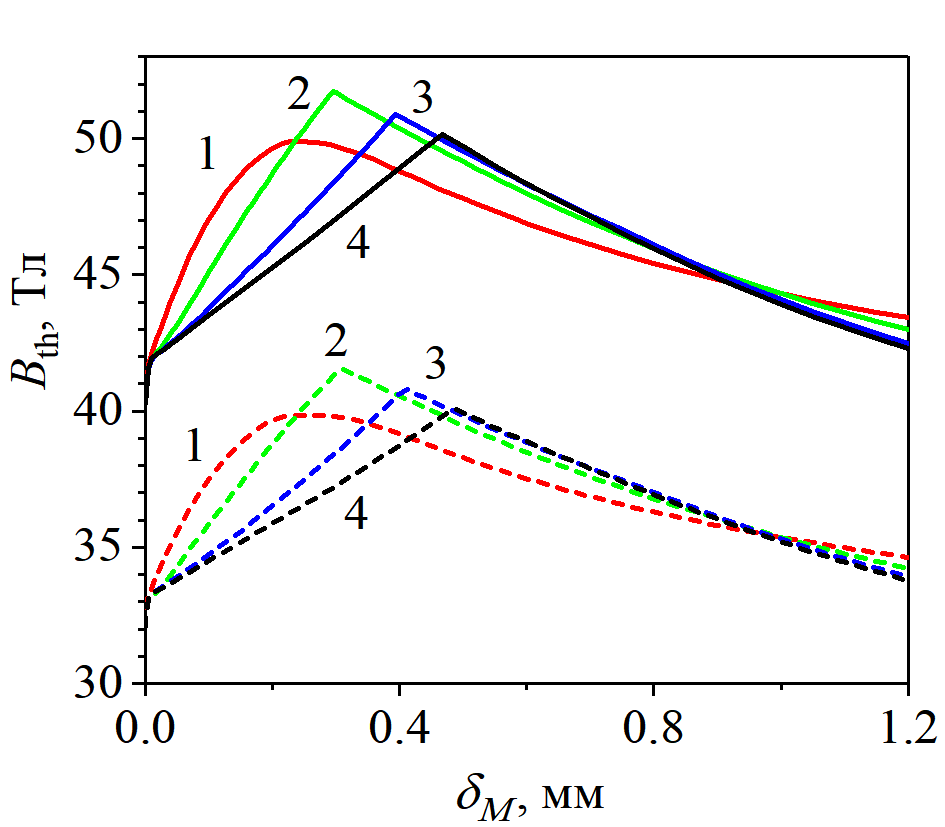
Зависимость порогового поля Bth от глубины модификации при «амплитуде» γ0 = 1,5 и параметре Nγ = 1 (линии 1), 2 (линии 2), 6 (линии 3) и Nγ → ∞ (линии 4)

Рисунок 8 - Зависимость порогового поля Bth от глубины модификации при «амплитуде» γ0 = 1,5 и параметре Nγ = 1 (линии 1), 2 (линии 2), 6 (линии 3) и Nγ → ∞ (линии 4)

Примечание: щтриховые линии соответствуют исходному контуру с сопротивлением Re,0; сплошные линии — Re = 10Re,0

DOI:10.60797/IRJ.2025.155.57.8
На рис. 8 представлены зависимости порогового поля
от глубины модификации
при значениях
, 2, 6 и для ступенчатого профиля
как для исходного контура с сопротивлением
, так и для контура с сопротивлением
. Видим, что повышение порогового поля, достигаемое за счет увеличения диссипативных свойств RLC-контура, практически не зависит от используемых модифицирующих удельное сопротивление поверхностных слоев: сплошные и штриховые линии на рис. 8 почти эквидистантны. Совместное использование высокого сопротивления контура
и наиболее эффективной из представленных модификации (
, 
 мм) позволяет в итоге повысить предельную амплитуду импульсного поля
с 32 Тл до 52 Тл.

4. Заключение

Построена математическая модель, описывающая поведение индукторной системы «RLC-контур + одновитковый соленоид + концентратор», которая учитывает динамику разрядного электрического контура и диффузию магнитных полей как в соленоид, так и в концентратор. На основе построенной модели численно получено самосогласованное решение уравнения динамики контура и уравнений, описывающих пространственные распределения в индукторе и концентраторе магнитных и температурных полей, механических напряжений и деформаций. Начальные значения сопротивления и индуктивности RLC-контура

определены из условия наилучшего согласия теоретической модели с экспериментальными данными по временным разверткам тока контура и генерируемого магнитного поля. Теоретически исследована возможность существенного повышения амплитуды
генерируемых импульсных магнитных полей индукторной системой без достижения опасного порога инициализации механизма малоцикловой усталости. Проведённый анализ влияния размеров индукторной системы показал, что наибольшие пороговые поля
достигаются при внутреннем радиусе от 4 до 5 толщин скин-слоя стального проводника. Повышение амплитуды порогового поля возможно либо за счет использования для концентратора материалов с более высокими значениями удельной проводимости (при неизменных прочих характеристиках), либо за счет повышения собственного сопротивления
электрического разрядного контура. Так, в сравнении с параметрами экспериментальной установки в работах
,
,
, увеличение
в 10 раз при неизменной собственной индуктивности
контура позволяет повысить амплитуду импульсных магнитных полей, генерируемых используемыми стальными концентраторами без угрозы их разрушения, примерно на 25%, с 32 Тл до 40 Тл. Совместно с применением модифицирующих поверхностных слоев с относительной невысокой амплитудой модификации, при которой удельное сопротивление
на рабочей поверхности концентратора превышает удельной сопротивление в толще материала
в 2.5 раза, обнаруженный эффект позволяет безопасно достигать еще более высоких магнитных полей — порядка 50 Тл.

Additional materials

Not specified

Financing

Авторы не получали финансовой поддержки для проведения исследования, написания и публикации статьи

Acknowledgements

Not specified

Conflicts of interests

Not specified

References

  • Ostropiko Ye.S. Magnitno-impulsnoe deformirovanie splava TiNi: eksperiment i raschet [Magnetic-pulse deformation of TiNi alloy: experiment and calculation] / Ye.S. Ostropiko, S.G. Magazinov, S.I. Krivosheev // ZhTF [Technical Physics]. — 2022. — Vol. 92. — Iss. 1. — P. 174–182. [in Russian]

  • Boltachev G.Sh. Theory of the magnetic pulsed compaction of nanosized powders / G.Sh. Boltachev, K.A. Nagayev, S.N. Paranin [et al.] // Nanomaterials: Properties, Preparation and Processes. — New-York: Nova Science Publishers, 2010. — 412 p.

  • Olevsky E.A.

    Modeling and optimization of uniaxial magnetic pulse compaction of nanopowders
    / E.A. Olevsky, A.A. Bokov, G.Sh. Boltachev et al. //
    Acta Mechanica
    . — 2012. — Vol. 224. — Iss. 12. — P. 3177–3195.

  • Boltachev G.Sh. Dinamika tsilindricheskikh provodyashchikh obolochek v prodolnom impulsnom magnitnom pole [Dynamics of cylindrical conducting shells in a longitudinal pulsed magnetic field] / G.Sh. Boltachev, N.B. Volkov, S.N. Paranin [et al.] // ZhTF [Technical Physics]. — 2010. — Vol. 80. — Iss. 6 . — P. 1–9. [in Russian]

  • Strizhakov Ye.L. Visokovoltnaya impulsnaya kondensatornaya svarka raznorodnikh detalei [High voltage pulse capacitor welding of diversified parts] / Ye.L. Strizhakov, S.V. Neskromnii, R.V. Merkulov // SVARKA I DIAGNOSTIKA [Welding and Diagnostics]. — 2012. — Vol. 4. — P. 43–45. [in Russian]

  • Krutikov V.I.

    Magnetic Pulse Pipe Welding End Caps Chromium Stainless Steels
    / V.I. Krutikov, S.N. Paranin, D.S. Koleuh et al. //
    Russian Physics Journal
    . — 2014. — Vol. 57. — № 11/3. — P. 264–268.

  • Spirin A.V.

    Effect of structural steel ion plasma nitriding on material durability in pulsed high magnetic fields
    / A.V. Spirin, V.I Krutikov, D.S. Koleukh et al. //
    IOP Conf. Series Journal of Physics Conf. Series
    . — 2017. — № 830. — P. 012080. — DOI: 10.1088/1742-6596/830/1/012080

  • Spirin A.V.

    Destruction Features of Steel Inductors with Nitrided Working Surface Under Strong Magnetic Field Generation
    . / A.V. Spirin, P.A. Russkikh, V.I. Krutikov et al.; — Tomsk: IEEE, 2018. — P. 148–153. DOI: 10.1109/ISHCE.2018.8521205

  • Spirin A.V.

    Surface modification of steel inductor as an attempt to enhance its durability in high pulsed magnetic fields
    / A.V. Spirin, G.Sh. Boltachev, V.I. Krutikov et al. //
    AIP Conf. Proc
    . — 2019. — Vol. 2174. — № 1. — P. 020163.

  • Russkikh P.A.

    Simulating the conductor with a nonuniform resistance under high-pulsed magnetic fields
    / P.A. Russkikh, G.S. Boltachev, S.N. Paranin //
    IEEE Trans. Plasma Sci
    . — 2021. — Vol. 49. — № 9. — P. 2463–2469.

  • Russkikh P.A. Khrupkoe razrushenie provodnika v silnom impulsnom magnitnom pole [Brittle fracture of a conductor in a strong pulsed magnetic field] / P.A. Russkikh, S.N. Paranin // ZhTF [Technical Physics]. — 2023. — Vol. 93. — Iss. 5. — P. 654–665. [in Russian]

  • Russkikh P.A. Sposobi povisheniya predelnogo impulsnogo magnitnogo polya, vizivayushchego razrushenie stalnogo induktora pri mnogokratnom vozdeistvii [Methods for Increasing the Threshold of a Pulsed Magnetic Field That Causes Steel Inductor Destruction under Repeated Impact] / P.A. Russkikh, G.Sh. Boltachev, S.N. Paranin // Izvestiya RAN. Seriya fizicheskaya [Proceedings of the Russian Academy of Sciences: Physics]. — 2023. — Vol. 87. — Iss. 11. — P. 1534–1540. [in Russian]

  • Krivosheev S.I.

    The impact of local current density increase on conductor destruction
    / S.I. Krivosheev, Yu.E. Adamian, D.I. Alekseev et al. //
    J. Phys. Conf
    . — 2019. — Vol. 1147. — P. 012033.

  • Herlach F.

    Strong and Ultrastrong Magnetic Fields and Their Applications
    / F. Herlach. — Berlin: Springer-Verlag, 1985. — 379 p.

  • Karpova I.M. Analiz deformatsionnoi stoikosti provodnikovikh materialov v silnom impulsnom magnitnom pole [Analysis of deformation resistance of conductor materials in a strong pulsed magnetic field] / I.M. Karpova, V.V. Titkov // ZhTF [Technical Physics]. — 1994. — Vol. 64. — Iss. 7. — P. 137–147. [in Russian]

  • Karpova I.M. Termouprugoplasticheskaya deformatsiya v skin-sloe impulsnogo solenoida i otsenka resursa provodnikovikh materialov v silnom magnitnom pole [Thermoelastic-plastic deformation in the skin layer of a pulsed solenoid and lifetime estimation of conductor materials in a strong magnetic field] / I.M. Karpova, V.V. Titkov // ZhTF [Technical Physics]. — 1995. — Vol. 65. — Iss. 6. — P. 54–63. [in Russian]

  • Karpova I.M.

    Analysis of methods of lowering heating and thermal stresses in coils in high pulsed magnetic fields
    . / I.M. Karpova, A.N. Semakhin, V.V. Titkov et al.; — New York: Nova science publishers, 1990. — P. 209–215.

  • Shneerson G.A.

    Polya i perexodny'e processy' v apparature sverxsil'ny'x tokov
    [
    Fields and transient processes in ultra-high current equipment
    ] / G.A. Shneerson. — Moskva: E'nergoatomizdat, 1992. — 413 p. [in Russian]

  • Spirin A.V.

    Study of resistivity distribution in modified surface steel
    / A.V. Spirin, E.Y. Zaytsev, S.N. Paranin //
    IEEE Trans. Magn
    . — 2022. — Vol. 58. — № 6. — P. 8401107.

  • Shneerson G.A.

    Conceptual model of a quasi-force-free magnet of small volume with inertial retention of its end part
    / G.A. Shneerson, A.A. Parfentiev, V.V. Titkov et al. //
    Tech. Phys. Lett
    . — 2021. — Vol. 47. — P. 573–576.

  • Karpova I.M. Minimizatsiya maksimalnogo lokalnogo nagreva provodnika v impulsnom elektromagnitnom pole pri ispolzovanii sloistoi provodyashchei sredi [Minimization of maximum local heating of a conductor in a pulsed electromagnetic field using a layered conductive medium] / I.M. Karpova, V.V. Titkov // Elektrichestvo [Electricity]. — 1999. — Vol. 12. — Iss. 55. — P. 55–60. [in Russian]

  • Sedov L.I.

    Mexanika sploshnoj sredy', t. 2
    [
    Continuum mechanics, vol. 2
    ] / L.I. Sedov. — Moskva: Nauka, 1976. — 576 p. [in Russian]

Review

All articles are peer-reviewed. But the reviewer or the author of the article chose not to publish a review of this article in the public domain. The review can be provided to the competent authorities upon request.

Author information

AffiliationInstitute of Electrophysics of the Ural Branch of the Russian Academy of Sciences, Ekaterinburg, Russian Federation
Role:Author, Visualization, Research data analysis
ORCID:0000-0001-5095-2278
ELIBRARY AUTHOR ID:1071025
AffiliationInstitute of Electrophysics of the Ural Branch of the Russian Academy of Sciences, Ekaterinburg, Russian Federation
Role:Author, Management, Writing, reviewing and editing, Analysis
ORCID:0000-0002-0598-2627
ELIBRARY AUTHOR ID:38193
RESEARCHER ID:N-7075-2015

Article metrics

Views:462
Downloads:9
Views
Total:
Views:462