NUMERICAL SIMULATION OF PICOSECOND MAGNETIC COMPRESSION LINES
NUMERICAL SIMULATION OF PICOSECOND MAGNETIC COMPRESSION LINES
Abstract
Magnetic compression lines (MCLs) are promising solid-state devices for producing picosecond pulses with power of tens of gigawatts. This paper describes a numerical model of MCL based on the coupled solution of Maxwell’s equations and Landau-Lifshitz-Gilbert equation in the COMSOL Multiphysics software package. The used boundary conditions, solver settings, and finite element mesh settings are described. An explicit method for taking into account losses in line conductors for time domain calculations is proposed. The model is implemented in two-dimensional axisymmetric and three-dimensional formulations.
After optimization, the model shows good agreement with experimental data. Using the created model, the influence of ohmic losses and higher-order modes on the formation of a pulse in the MCL was analyzed.
1. Введение
В последние годы активное развитие получил новый тип устройств мощной импульсной техники - линии магнитной компрессии (MCL от англ. Magnetic Compression Lines). При помощи MCL были получены импульсы пикосекундной длительности с рекордными амплитудными параметрами. MCL являются разновидностью гиромагнитных импульсных устройств, то есть устройств, работа которых основана на взаимодействии магнитного поля, созданного импульсом тока, и вектора намагниченности в намагниченной среде, например в феррите. Одними из наиболее изученных гиромагнитных импульсных устройств являются гиромагнитные нелинейные линии передачи (GNLTL), перспективные источники импульсного сверхвысокочастотного излучения высокой мощности , . GNLTL представляет из себя двухсвязную линию передачи, обычно коаксиального типа, частично или полностью заполненную ферритовым материалом (рисунок 1, a). Феррит намагничивается до состояния глубокого насыщения внешним соленоидом или сборкой из постоянных магнитов. Когда на вход такой линии подается импульс с наносекундным или субнаносекундным фронтом, при его распространении магнитное поле импульса вызывает прецессию вектора намагниченности M вокруг вектора эффективного магнитного поля Heff, которое представляет из себя векторную сумму магнитного поля внешнего соленоида, магнитного поля импульса, и размагничивающих полей в феррите. Эта прецессия распространяется вдоль линии когерентно в виде волны намагниченности, модулируя импульс сверхвысокочастотными колебаниями с максимальной мощностью до нескольких сотен МВт. Частота колебаний приблизительно равна частоте, на которой выполняется условие фазового синхронизма электромагнитной квази-Т волны и волны намагниченности, и обычно лежит в диапазоне 1-20 ГГц .
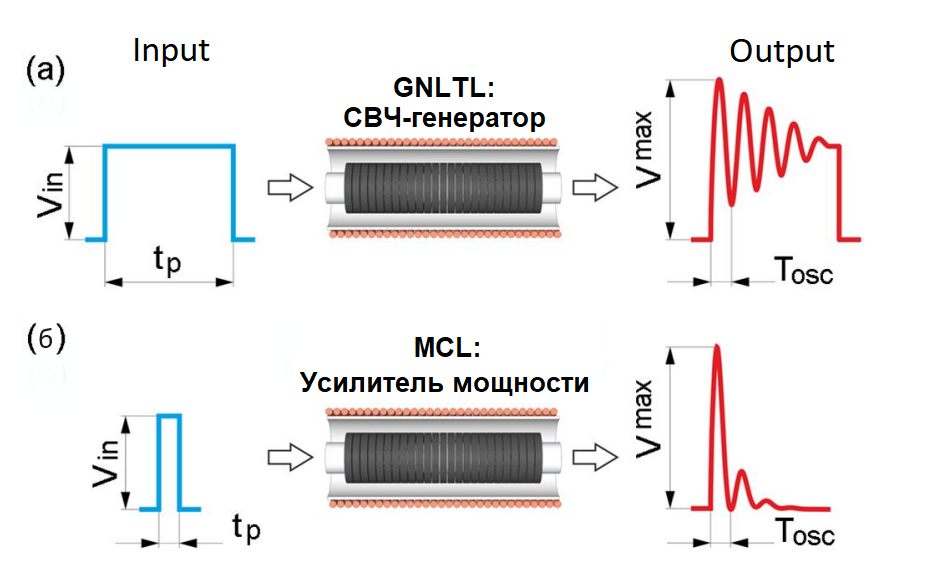
Рисунок 1 - Два режима работы коаксиальной линии передачи, заполненной ферритом:
а - генератор СВЧ колебаний; б - усилитель мощности монополярных импульсов
2. Описание численной модели
При построении модели целью было поставлено наименьшее возможное количество упрощений, чтобы учесть все возможные электродинамические эффекты в коаксиальной линии. По этой причине не была использована популярная расчётная методика для GNLTL , основывающаяся на телеграфных уравнениях, поскольку применение последних справедливо только для линий передач с поперечной Т-волной. Поскольку и GNLTL, и MCL состоят из двух диэлектрических слоёв с разными свойствами (феррит и изолятор), на их границе раздела возникает составляющая электрического поля, направленная вдоль направления распространения волны, так что рассмотрение такой волны как чисто поперечной являлось бы упрощением. Описанная волна обладает частотной дисперсией и носит название квази-Т . Исходя из этого, было решено построить модель основываясь на уравнениях Максвелла. Для этого, уравнения были выражены через магнитный векторный потенциал A, определяемый как B≡∇×A. Если при этом принять калибровку Вейля для векторного потенциала (она же калибровка Гамильтона) , то есть тождественно приравнять электростатический потенциал к нулю (что в принятой калибровке не снижает общности уравнений), три из четырёх уравнений Максвелла (закон Гаусса, закон Гаусса для магнитного поля, и закон Фарадея-Максвелла), выполняются автоматически. Оставшееся уравнение (1) (закон Ампера-Максвелла) может быть преобразовано в форму, зависящую только от A, как продемонстрировано в шагах (2)-(5).
Из определения A и калибровки Вейля следует, что напряжённость электрического поля E и магнитная индукция B определяются, как (3) и (4) соответственно.
Подставляя (3) и (4) в (2), получим окончательное выражение (5).
Здесь μ0 – магнитная постоянная, ε0 – диэлектрическая постоянная, ε – относительная диэлектрическая проницаемость среды. Чтобы учесть нелинейные свойства феррита, в уравнение было включено слагаемое намагниченности M.
Динамическое поведение намагниченности в феррите в состоянии магнитного насыщения может быть описано макроскопически уравнением Ландау-Лифшица с диссипативным слагаемым в форме Гильберта (6). Это уравнение также называют уравнением ЛЛГ.
Здесь γ – гиромагнитное отношение электрона, равное 1.76⋅1011 рад/(с Тл), μ0 – магнитная постоянная, M – вектор намагниченности феррита, Ms – величина намагниченности насыщения феррита, Heff – эффективная напряжённость магнитного поля в феррите, α – безразмерный коэффициент затухания Гильберта, обычно лежащий в пределах 0.1-1 для напряжённостей магнитного поля около 106 А/м , но не имеющий принципиального верхнего ограничения. В уравнении ЛЛГ первое слагаемое в правой части имеет смысл крутящего момента, перпендикулярного к плоскости, определяемой векторами M и Heff, который вызывает вращение (прецессию) вектора M вокруг вектора Heff. Второе слагаемое необходимо для учёта затухания прецессии. Его смысл состоит в отклонении крутящего момента, действующего на M, в сторону Heff, фактически направляя движение вектора M к вектору Heff. Таким образом, поведение M, определяемое данным уравнением, состоит в том, что при относительно медленных изменениях направления магнитного поля вектор M движется параллельно вектору Heff, но при быстрых изменениях направления Heff, вектор M переходит в новое, параллельное вектору Heff положение, путём прецессирующего движения.
Heff представляет собой суммарное эффективное магнитное поле внутри феррита, то есть векторную сумму внешнего магнитного поля, создаваемого подмагничивающим соленоидом, магнитного поля входного импульса, распространяющегося по линии, и размагничивающих полей. Размагничивающие поля в данном случае можно подразделить на статические и динамические. Статическая составляющая размагничивающего поля возникает всегда, когда тело произвольной формы с отличной от окружающей среды магнитной проницаемостью пронизывается магнитными линиями. Чтобы удовлетворять граничным условиям на границах тела и среды, напряжённость магнитного поля H перераспределяется, из-за чего внутри образца H снижается. Это явление можно рассматривать как возникновение внутреннего магнитного поля, направленного так, что его векторная сумма с внешним полем по величине оказывается ниже внешнего поля. Это внутреннее поле и называется статическим размагничивающим полем. Динамическая компонента размагничивающего поля в MCL возникает, когда намагниченность M изменяет своё направление под действием магнитного поля входного импульса. Изменение направления намагниченности приводит к изменению магнитного потока, пронизывающего поперечное сечение линии, что индуцирует токи проводимости и смещения в проводниках MCL и в пространстве между проводниками, соответственно. Эти токи создают свои собственные магнитные поля, которые, в зависимости от направления, усиливают или ослабляют суммарное магнитное поле. При достаточно быстрых изменениях направления M, характерных для GNLTL и MCL, влияние этих наведённых токов может быть весьма велико.
Чтобы распределение магнитного поля внешнего соленоида наиболее соответствовало реальному, в модель был включен предварительный шаг, в ходе которого решается магнитостатическая задача, согласно уравнению (7), в результате чего находится распределение магнитного поля, создаваемое в MCL внешним соленоидом известной геометрии, в который подаётся плотность тока J, однородная по сечению соленоида. Феррит задан как нелинейный материал, амплитуда намагниченности которого является функцией напряжённости магнитного поля, а направление намагниченности совпадает с направлением магнитного поля (как и должно быть в магнитостатическом случае). Такой расчёт автоматически учитывает величину и распределение статических размагничивающих полей в сечении феррита.
Распределения A и M, найденные на предварительном шаге, затем передаются в динамическую часть расчёта в качестве начальных условий для уравнений (5) и (6) соответственно. Намагниченность M, определяемая по уравнению (6), подставляется в слагаемое уравнения (5), содержащее M, что обеспечивает связь уравнений. Напряжённость поля H, вычисляемая из найденного по уравнению (5) векторного потенциала как H = ∇×(A/µ0), подставляется в качестве Heff в уравнение (6). С учётом предварительного шага поле H уже содержит в себе внешнее подмагничивающее поле, магнитное поле импульса, и статическое размагничивающее поле. Когда направление M изменяется, в результате чего, в соответствии с общим уравнением (5), индуцируются динамические размагничивающие поля, они также автоматически включаются в H. Таким образом, построенная модель учитывает все макроскопические способы взаимодействия H и M.
Для численного решения системы уравнений и создания необходимых граничных условий, был выбран полуграфический программный комплекс для численного моделирования COMSOL Multiphysics . Проводники коаксиальной линии задавались как границы, на которых устанавливалось граничное условие «Идеальный электрический проводник» (PEC). В качестве согласованной нагрузки на конце линии устанавливалось поглощающее граничное условие первого порядка для плоской волны, падающей в направлении продольной оси MCL. Входной импульс подавался в линию с помощью установленного на входе линии поглощающего граничного условия, на котором дополнительно задавалась падающая извне плоская волна. Структура поля падающей волны была установлена равной известной структуре поля Т-волны для коаксиальной линии, которая для напряжённости электрического поля E записывается следующим образом:
Здесь r – радиальная координата поперечного сечения коаксиальной линии, D и d – внешний и внутренний диаметры коаксиальной линии соответственно, U(t) – зависимость входного напряжения от времени (форма входного импульса). Поскольку в основе такого способа возбуждения лежит поглощающее граничное условие, любые отраженные от неоднородностей линии волны будут им поглощены, что минимизирует влияние таких отражений на процессы, происходящие в модели.
Геометрически модель была реализована в двух постановках (рис. 2): двумерная осесимметричная (2D), в которой предполагается, что у искомых величин отсутствует зависимость от азимутального угла, и полная трёхмерная (3D), в которой отсутствуют упрощения, связанные с пространственной симметрией. Преимуществом 2D модели перед 3D является гораздо меньшее время расчёта, в то время как её очевидным недостатком является возможность наблюдать и учитывать только осесимметричные эффекты.
COMSOL решает описанную систему уравнений, используя метод конечных элементов. Система уравнений Максвелла и ЛЛГ является нелинейной, поскольку изменение вектора H вызывает движение вектора M, что в свою очередь вызывает новое изменение вектора H, и так далее. В настройках решателя COMSOL выставлена настройка «Fully Coupled», то есть система уравнений связана общей матрицей коэффициентов (другая опция – «Segregated», когда на каждом временном шаге решается сначала одно уравнение, после чего значения величин подставляются во второе уравнение). Обновление матрицы системы (матрицы Якоби) установлено на автоматическое («Automatic»). Указанные настройки решателя обеспечивают хорошую сходимость для нелинейных систем.
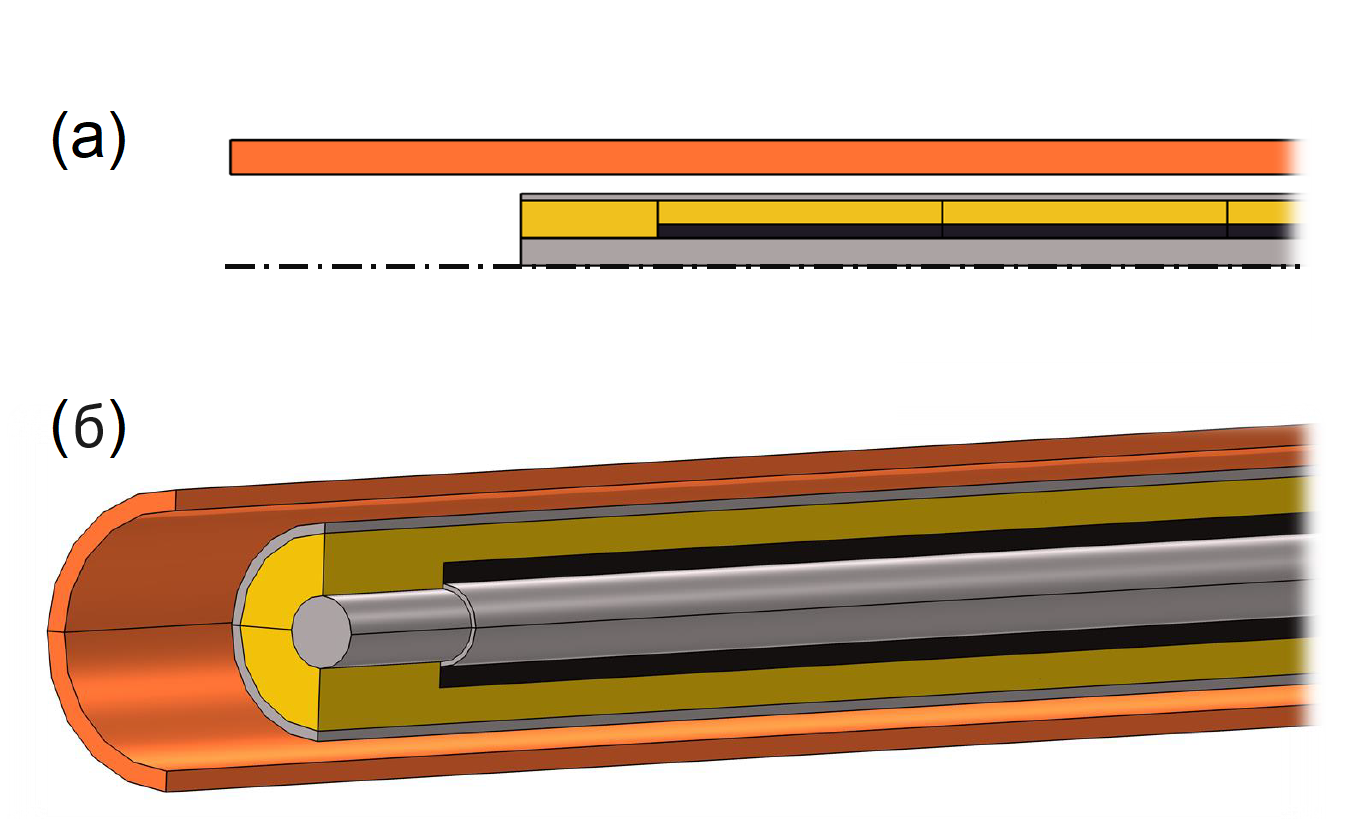
Рисунок 2 - Рисунок 2 - Варианты геометрии созданной модели:
a – двумерная осесимметричная геометрия; б – трёхмерная геометрия
Примечание: цветом обозначены: оранжевым – внешний соленоид, жёлтым – трансформаторное масло, чёрным – феррит, серым – проводники линии
3. Результаты расчёта по составленной модели
Созданная модель была оптимизирована для наилучшего согласия с экспериментальными данными. Оптимизация заключалась в подборе неизвестных параметров: коэффициента затухания Гильберта α, а также суммарного коэффициента ослабления kloss, на который умножалась расчётная осциллограмма выходного импульса, чтобы учесть влияние отсутствующих в модели механизмов потери энергии, приводящих к снижению амплитуды импульса. В качестве экспериментальных данных были взяты выходные импульсы линий MCL3_38 и MCL3_50, приведённые в работе . Остальные свойства материалов в модели были взяты согласно таблице 1.
Таблица 1 - Свойства материалов в модели
Свойство | Материал | Значение | Примечания |
Диэлектрическая проницаемость ε | Трансформаторное масло | 2.25 | Справочное значение |
Диэлектрическая проницаемость ε | Феррит марки М200ВНП | 12.6±0.3 | Измеренное значение в области высоких частот (100 кГц – 100 МГц) |
Намагниченность насыщения Ms | Феррит марки М200ВНП | 300±15 кА/м | Измеренное значение на частоте 50 Гц в поле напряжённостью до 35 кА/м |
Остаточная индукция Br | Феррит марки М200ВНП | 0.26±0.01 Тл | То же |
Удельное сопротивление ρ | Трансформаторное масло | 1016 Ом⸱м | Справочное значение |
Удельное сопротивление ρ | Феррит марки М200ВНП | 3⸱107±1.5⸱107 Ом⸱м | Измеренное значение на постоянном токе |
Значениями параметров, при которых достигается наилучшее согласие с экспериментальными данными, оказались α=0.2, kloss=0.92. Сравнение расчётной и экспериментальной осциллограмм после оптимизации показано на рис. 3. Наблюдается хорошее согласие расчёта и экспериментальных данных, особенно в области главного и вторичного пиков формируемого импульса.
В ходе расчётов было установлено, что в двумерной геометрической постановке модель также может адекватно учитывать потери в проводниках линии в явном виде, то есть без применения импедансных граничных условий. Для этого необходимо включить приповерхностный слой проводников линии в область расчёта с помощью конечно-элементной сетки типа Mapped толщиной в 2-3 элемента. При этом толщина одного элемента должна составлять характерную глубину диффузии магнитного поля в проводник dдифф за длительность импульса tи :
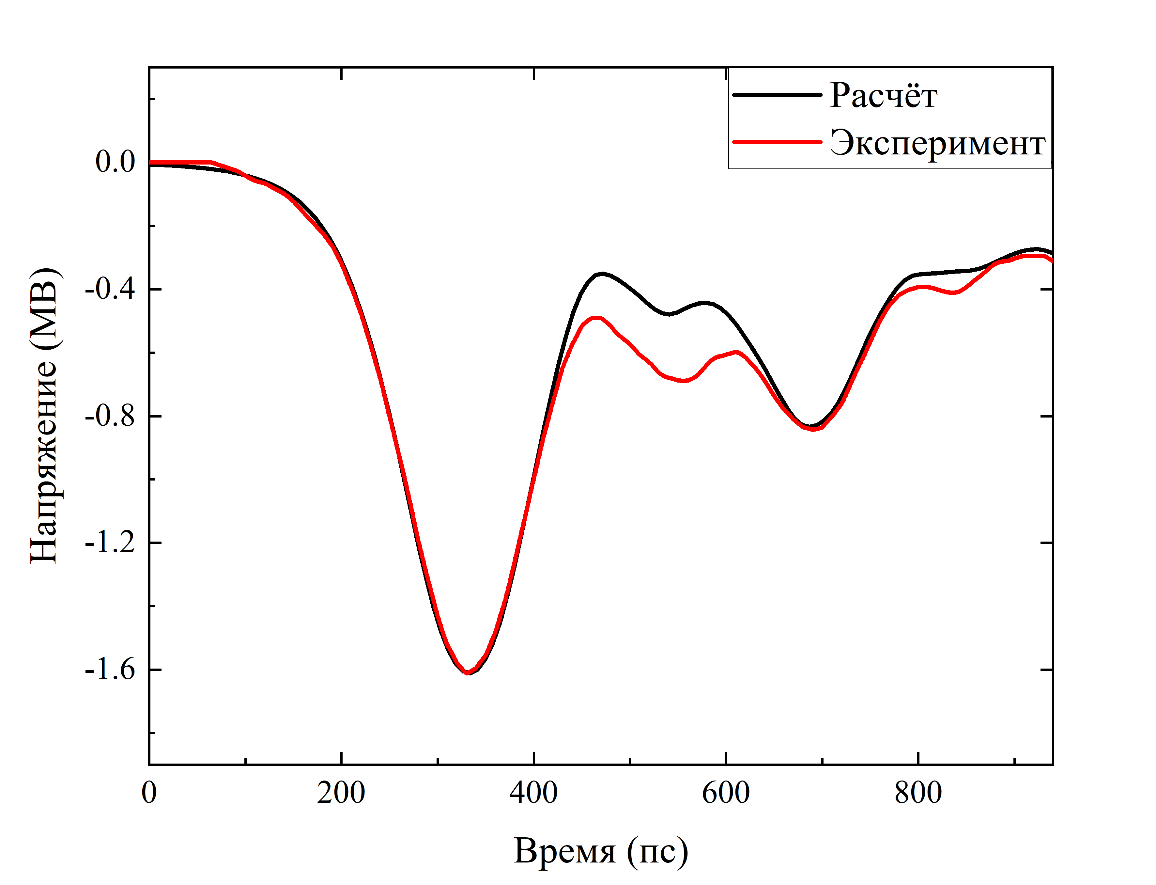
Рисунок 3 - Сравнение расчётной и экспериментальной осциллограмм для линии MCL3_38
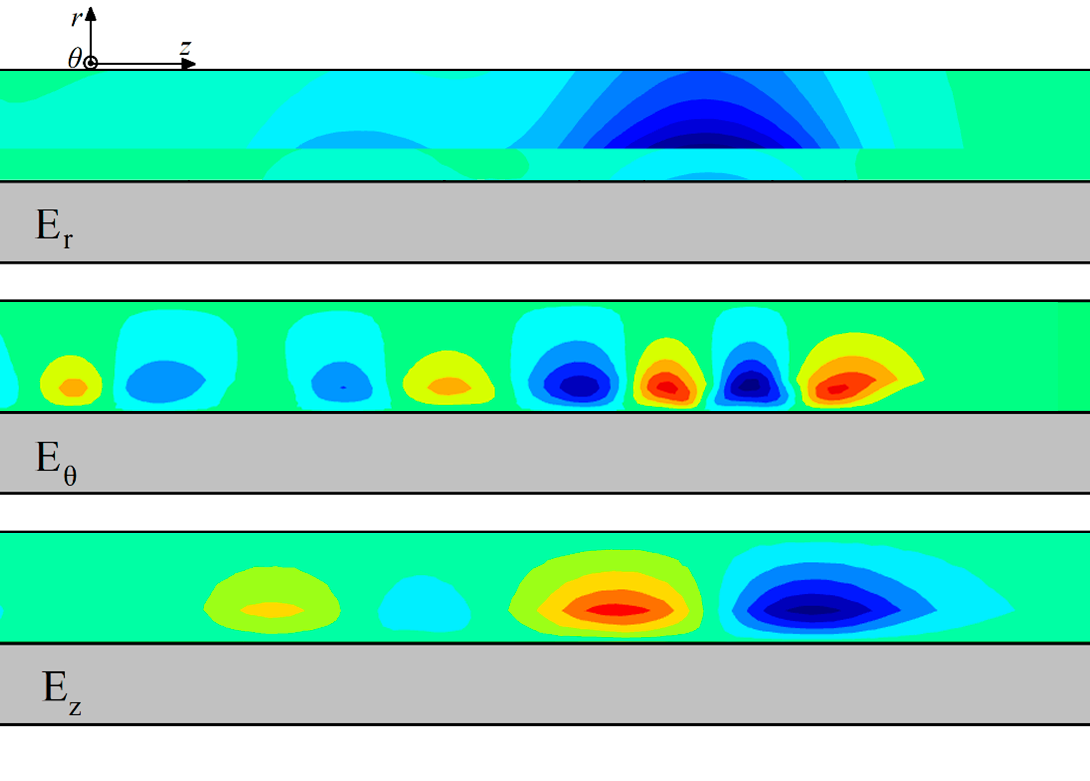
Рисунок 4 - Картина электрического поля в линии MCL3_38 при распространении по ней импульса
Примечание: пояснения см. в тексте
Для изучения влияния волны H01 на формирование выходного импульса было сделано следующее. В расчёте была введена высокая анизотропная электрическая проводимость феррита в азимутальном направлении. Такая проводимость не оказывает влияния на ёмкостные токи основной волны, текущие в радиальном направлении, но эффективно рассеивает энергию индуцируемых кольцевых токов в джоулево тепло. Это привело к исчезновению волны H01 в расчёте, при этом форма выходного импульса осталась неизменной. Это позволяет сделать вывод, что высшие волны магнитного типа, симметричные по азимуту, присутствуют в MCL, но не необходимы для её работы.
Проведённый анализ не позволяет установить влияние на формирование импульса высших волн электрического типа, симметричных по азимуту, например волны E01, так как их компоненты полей перекрываются с компонентами полей основной волны квази-Т (которая сама по себе является волной электрического типа, на низких частотах вырождающейся в Т-волну), поэтому провести между ними чёткое разграничение в расчёте затруднительно. Тем не менее, из проведённого анализа можно сделать вывод, что формирование импульса в MCL обеспечивается взаимодействием нелинейного ферритового материала с одной или несколькими волнами электрического типа, в качестве которых выступают либо основная волна двухслойной коаксиальной линии типа квази-Т (квази-ТЕМ), либо её суперпозиция с высшими волнами электрического типа, симметричными по азимуту (например, E01). Отметим, что этот результат согласуется с результатом, полученным для ферритовых линий, работающих в режиме GNLTL, в работе .
4. Заключение
В ходе данного исследования была создана расчётная модель пикосекундной мультигигаваттной линии магнитной компрессии, основывающаяся на уравнениях Максвелла и уравнении Ландау-Лифшица-Гильберта, описывающем динамическое поведение намагниченности в феррите. Система уравнений решается численно с помощью программного комплекса COMSOL Multiphysics в двумерной и трёхмерной геометрических постановках. Модель показывает хорошее согласие с имеющимися экспериментальными данными. Также была предложена явная методика учёта омических потерь в проводниках линии при расчёте во временной области, показывающая хорошее согласие с аналитическими решениями.
Исследования процессов, происходящих в MCL, с помощью построенной модели, показали, что на формирование импульса в MCL не оказывают значительного влияния омические потери в проводниках линии, высшие волны двухслойной коаксиальной линии магнитного и электрического типов с азимутальным индексом 1 и выше, а также симметричные по азимуту магнитные волны (с азимутальным индексом 0). Таким образом показано, что процесс формирования импульса в линии магнитной компрессии основывается на взаимодействии нелинейного ферритового материала с основной волной двухслойной коаксиальной линии типа квази-Т, или с суперпозицией волны квази-Т и высших волн электрического типа с азимутальным индексом 0.
