RESIDUAL ELECTRICAL RESISTANCE OF METALS AND ALLOYS WITH VACANCIES
RESIDUAL ELECTRICAL RESISTANCE OF METALS AND ALLOYS WITH VACANCIES
Abstract
The influence of vacancies on the residual electrical resistance of ordered and disordered alloys, as well as pure metals, has been studied in the coherent potential approximation. For ordered and disordered alloys, this was done in the limit of weak scattering in the A-B system of atoms, taking into account the smallness of the vacancy concentration, but at the same time the scattering on vacancies was taken into account accurately. Numerical calculations are performed for disordered alloys without the use of small parameter expansions. It is concluded that the appearance of vacancies leads to an increase in residual electrical resistance at any concentrations of the alloy components and any values of the degree of long-range order. An exact analytical solution of the problem is obtained for pure metals. The calculated values of the vacancy contribution to resistance for Cu, Ag, Au, Pb, Al are in agreement with experimental data.
1. Введение
После длительного отжига при достаточно высоких температурах в металлах и сплавах устанавливается довольно высокая концентрация равновесных вакансий, которая может достигать величин порядка 0,1 – 1 атомного процента при температурах, близких к точке плавления . Быстрая закалка металлов и сплавов позволяет сохранить «термические» вакансии и при достаточно низких температурах. Как и другие несовершенства кристаллической решетки, неравновесные вакансии будут вносить свой вклад в остаточное сопротивление металлов и сплавов.
Влияние вакансий на остаточное электросопротивление сплавов изучалось в (для полностью неупорядоченных сплавов) и в , (для частично упорядоченных сплавов). Расчеты проводились в рамках метода кинетического уравнения, который применим лишь при условии малости потенциала рассеяния. В случае рассеяния на вакансиях это условие заведомо не выполняется . Поэтому результаты работ , , носят чисто качественный характер и не могут быть применены к реальным сплавам.
В теории сплавов широко используется приближение когерентного потенциала (ПКП) , в котором нет ограничений на потенциал рассеяния. Целью данной работы является применение ПКП для расчета остаточного электросопротивления упорядочивающихся и неупорядоченных сплавов, а также металлов с вакансиями.
Остаточное электросопротивление бинарных упорядочивающихся сплавов детально исследовалось нами в ; для тройных упорядочивающихся сплавов этот вопрос рассмотрен в работах , . Влияние различных факторов на концентрацию вакансий в сплавах исследовалось нами в , , , .
2. Остаточное электросопротивление бинарных упорядочивающихся сплавов с вакансиями
Обратимся к изучению бинарного упорядочивающегося сплава (БУС) ОЦК-структуры с вакансиями, пренебрегая при этом геометрическими искажениями решетки вблизи вакансий. Интересуясь удельными характеристиками сплава, рассмотрим основную область кристалла, содержащую N узлов. В этом случае когерентные потенциалы подрешеток могут быть найдены из уравнений ПКП для тройных упорядочивающихся сплавов (ТУС) (см.
), модифицированных с учетом того, что роль атомов третьей компоненты в исследуемой системе теперь играют вакантные узлы. Обозначим черезВыпишем t -матрицу рассеяния вакантного узла l –й подрешетки
В этой формуле – «атомный уровень» вакантного узла,
– когерентный потенциал,
-й подрешетки, функция
задается соотношениями
Здесь плотность электронных состояний, соответствующая трансляционно-инвариантному гамильтониану, аппроксимирована полуэллиптической кривой с полушириной равной единице.
Величины имеют порядок единицы (в единицах полуширины зоны проводимости). Как уже указывалось,
(в тех же единицах). В работе было даже принято
. Тогда
, и, пренебрегая единицей в знаменателе (1), получим
Это соотношение при описании сплавов без вакансий обычно называют пределом сильного рассеяния , . Отметим, что предел сильного рассеяния неприменим для описания металлических сплавов без вакансий, существующих во всем концентрационном диапазоне, т.к. в этом приближении при некоторой концентрации сплав неизбежно теряет металлические свойства. По-видимому, формула (3) дает адекватное описание именно в случае рассеяния электронов на вакансиях.
С учетом сказанного, уравнения для нахождения когерентных потенциалов подрешеток приобретают вид :
Система уравнений (4) описывает ТУС, в котором локализация электронов вблизи атомов третьей компоненты (вакансий) невозможна.
Далее мы исследуем аналитически случай слабого рассеяния в системе A-Bатомов, полагая однако рассеяние на вакансиях будем учитывать точно. Здесь
– атомный уровень компоненты
нашего сплава
. В пределе слабого рассеяния уравнения для когерентных потенциалов решаются итерациями, малым параметром задачи при этом является величина
. В нашей модели БУС с вакансиями помимо
малыми будут также величины
Проведем итерационное решение уравнений (4) с точностью до членов, квадратичных по
и линейных по
Рассмотрим случай, когда энергия Ферми
находится далеко от щели, появляющейся в приближении виртуального кристалла в плотности электронных состояний сплава. В итоге для величины
приходим к формуле
в которой, – число атомов сорта
в сплаве,
– число вакансий на
-й подрешетке,
концентрация атомов сорта
в сплаве,
– концентрация вакансий на
-й подрешетке,
– параметр дальнего порядка для БУС-ОЦК без вакансий.
В работе было показано, что в пределе слабого рассеяния в системе A-Bатомов в случае, когда энергия Ферми находится вдали от щели в плотности электронных состояний, электросопротивление БУС пропорционально
. Поскольку в ходе преобразований мы удерживаем лишь первые неисчезающие члены, имеющие порядок
и
, можно считать, что коэффициент пропорциональности между этими величинами не зависит от
и
. Таким образом для остаточного электросопротивления БУС с вакансиями получаем
где – электросопротивление БУС без вакансий,
– вклад в остаточное электросопротивление, обусловленный вакансиями,
– коэффициент пропорциональности, не зависящий от
и
.
Как видно из формул (7) – (9), в рассмотренном нами приближении вакансии приводят к увеличению остаточного электросопротивления сплава при любых концентрациях компонент и любых значениях степени дальнего порядка. Этот вывод, полученный нами в ПКП, принципиально отличается от результатов, полученных методом кинетического уравнения, когда при некоторых условиях вакансионный вклад в сопротивление может стать отрицательным .
На рисунке 1а изображены концентрационные зависимости электросопротивления упорядоченного сплава с вакансиями (пунктирная линия) и без вакансий (сплошная линия) при максимальном порядке, полученные в . Видно, что для сплава с вакансиями существует концентрационный интервал, в котором вакансионный вклад в сопротивление отрицателен. Наши результаты для упорядоченных сплавов при максимальном порядке (7) – (9) приведены на рисунке 1б.
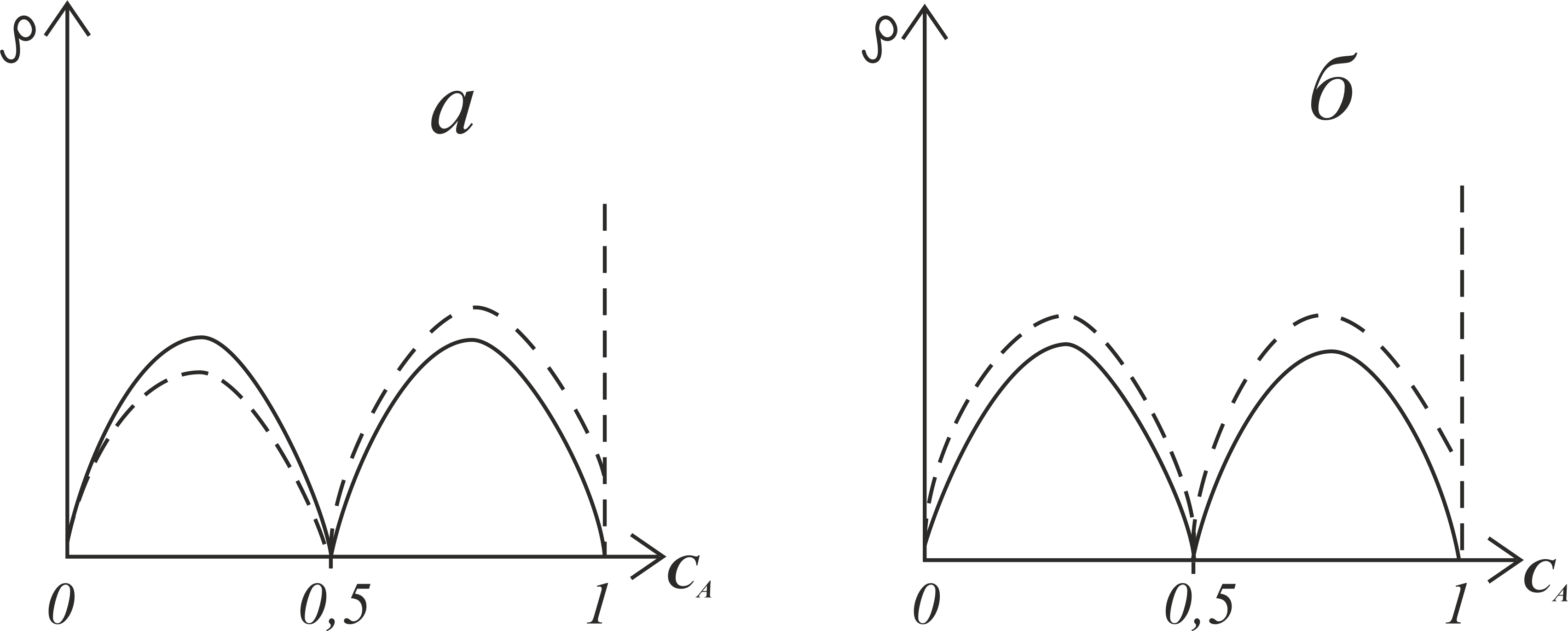
Рисунок 1 - Концентрационные зависимости остаточного электросопротивления упорядоченного сплава с вакансиями (пунктирная линия) и без вакансий (сплошная линия) при максимальном порядке
Примечание: эффект влияния вакансий на рисунке преувеличен
3. Остаточное электросопротивление неупорядоченных сплавов с вакансиями
В неупорядоченном состоянии подрешетки эквивалентны, поэтому эффективная среда, с помощью которой описывается исследуемая система, задается в одноузельном ПКП одним когерентным потенциалом . Для бинарного неупорядоченного сплава с вакансиями
находится из уравнения
которое получается из системы (4) в случае В этом уравнении
есть вероятность того, что узел решетки сплава занят либо атомом A или B, либо вакансией. Функция
определяется соотношениями
где резольвента Грина для эффективного гамильтониана,
и
функции Ваннье для узла
,
плотность электронных состояний, соответствующая трансляционно-инвариантному гамильтониану
. Далее функция
аппроксимируется полуэллиптической кривой, полуширина которой равна единице , . В этом случае
Тогда
Исключая из уравнения (10) с помощью (14), запишем (10) в эквивалентном виде
Последнее преобразуется в уравнение третьей степени относительно функции :
Здесь .
Определим вероятности следующим образом . Пусть в сплаве имеется
атомов сорта
,
атомов сорта
и
вакансий
. Назовем
соответственно концентрациями атомов сорта A, B и вакансий. Тогда
Через решения уравнения (16) плотность электронных состояний на узел выражается соотношением
а электропроводность – электросопротивление
описывается формулой
в которой энергия Ферми в сплаве с вакансиями определяется из уравнения
Здесь – заряд электрона,
– объем, приходящийся на один атом,
– максимальная скорость в полосе,
– число валентных электронов металла
.
С помощью соотношений (16) – (20) нами было проведено численное исследование влияния вакансий на плотность электронных состояний и остаточное электросопротивление сплава при следующих значениях параметров: и
и
и
Результаты расчетов позволяют сделать вывод, что при всех рассмотренных значениях параметров появление вакансий приводит к уменьшению плотности электронных состояний и увеличению остаточного электросопротивления сплава, причем эти эффекты тем сильнее, чем выше концентрация вакансий. Для ряда значений параметров результаты расчетов представлены на рисунке 2.
Для нахождения аналитического решения уравнения (10) используем наличие в нем малого параметра . Рассмотрим случай слабого рассеяния в системе A-B атомов, при этом рассеяние на вакансиях мы не считаем малым. Тогда с точностью до линейных по
и квадратичных по
членов получим для плотности электронных состояний неупорядоченного сплава с вакансиями
где Формула (21) позволяет сделать вывод, что появление вакансий приводит к качественно одинаковым изменениям плотности электронных состояний на узел в случаях слабого и промежуточного рассеяния: при появлении вакансий
уменьшается тем больше, чем выше концентрация вакансий.
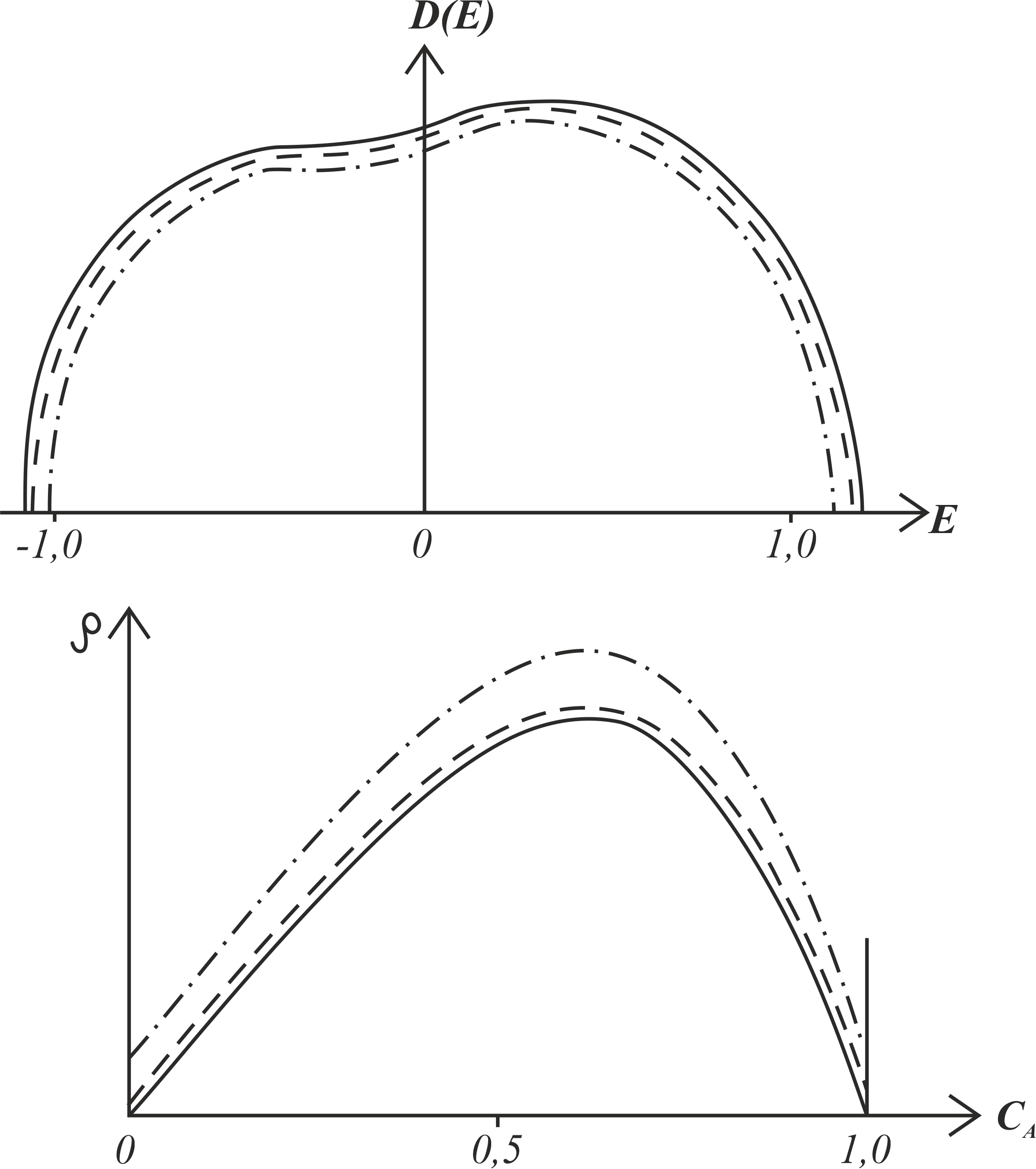
Рисунок 2 - Влияние вакансий на плотность электронных состояний D(E) (в этом случае выбраны значения параметров δ = 0,5 и сA = 0,6) и остаточное электросопротивление p неупорядоченных сплавов (здесь δ = 0, 25 и nA = nB = 0,2)
Примечание: эффект влияния вакансий на D(E) и p на рисунке преувеличен; сплошная линия -x=0, пунктирная линия -x=0,001 штрих-пунктирная линия -x=0,01 (x – концентрация вакансий)
где – остаточное сопротивление неупорядоченного сплава без вакансий,
– вакансионный вклад в сопротивление
В этих формулах
Из соотношений (23) и (24) видно, что зависимость от
определяется величиной
В изоэлектронных сплавах
не зависит от состава, и
сохраняет постоянное значение во всем интервале концентраций
.
Соотношения (23) представляют собой частный случай выражений (8) и (9), когда . Как видно из формул (8), (9), (23), в ПКП в пределе слабого рассеяния в системе A-B атомов вакансии всегда увеличивают сопротивление как упорядочивающихся, так и неупорядоченных сплавов. Этим наши результаты, основанные на использовании ПКП, отличаются от полученных методом кинетического уравнения выводов, допускающих наличие отрицательного вакансионного вклада. Для сравнения на рисунке 3 приведены графики концентрационной зависимости остаточного сопротивления неупорядоченных сплавов с вакансиями (пунктирная линия) и без вакансий (сплошная линия). Согласно , , , для неупорядоченных сплавов возможны два случая: вакансии приводят к увеличению остаточного сопротивления сплава при всех составах (см. рис. 3а); наличие вакансий обеспечивает уменьшение сопротивления в средней части концентрационного интервала (см. рис. 3б). Наши результаты показаны на рисунке 3а.
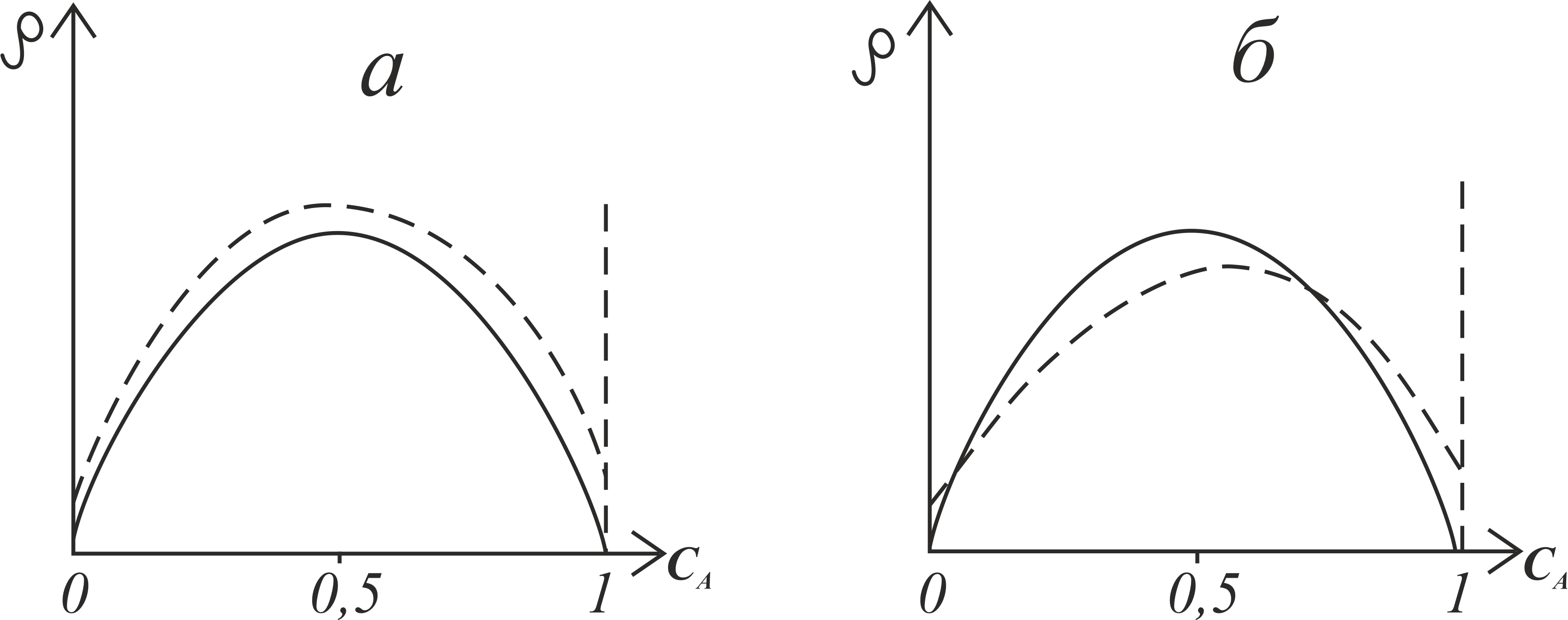
Рисунок 3 - Концентрационные зависимости остаточного электросопротивления p неупорядоченного сплава с вакансиями (пунктирная линия) и без вакансий (сплошная линия)
Примечание: эффект влияния вакансий на рисунке преувеличен
4. Влияние вакансий на электросопротивление чистых металлов
Перейдем к изучению свойств металлов с вакансиями. Если для упорядочивающихся и неупорядоченных сплавов возможен либо численный расчет, либо разложение по малым параметрам, то для чистых металлов с вакансиями доступно точное решение. Интересуясь удельными характеристиками металла, будем рассматривать основную область кристалла, содержащую узлов,
из которых вакантны. Тогда
есть концентрация вакансий, и когерентный потенциал металла с вакансиями
находится из уравнения
где – атомный уровень рассматриваемого металла. Данное уравнение является частным случаем уравнений (4) и (10) при
. Уравнение (25) дает
С учетом аппроксимации плотности электронных состояний металла полуэллиптической кривой с полушириной равной единице и соотношения (14) можно решить (26) относительно . Получим
В дальнейшем для удобства положим . Тогда плотность электронных состояний на узел в металле с вакансиями будет равна
Можно показать, что энергия Ферми металла с вакансиями задается выражением
где – энергия Ферми металла без вакансий.
Подставляя (27) – (29) в (19), запишем для остаточного электросопротивления металла с вакансиями
Здесь определяется соотношениями (24), в которых нужно положить
Отметим, что формула (30) описывает зависимость электросопротивления металла от концентрации вакансий точно. Поскольку
сохраним в (30) только линейный по x вклад
Формула (31) для содержит в коэффициенте
ряд параметров
которые трудно оценить теоретически. Однако, через эти же параметры выражается фононная часть электросопротивления металла
Здесь – температура плавления металла; коэффициент
определяется типом токонесущих электронных состояний: для s-состояний
для d-состояний
. Это позволяет записать
в виде
Используя экспериментальные значения и
– для ряда металлов , по формуле (33) можно вычислить соответствующие величины
. Результаты такого расчета приведены в Таблице 1, где указаны также экспериментальные данные о влиянии вакансий на сопротивление. При численных оценках
считалось, что во всех перечисленных металлах ток переносится s-электронами.
Таблица 1 - Значения сопротивления для разных металлов
Металл |
| |
Расч. | Эксп. | |
Cu | 0,98 | 1,2±0,6 |
Ag | 0,84 | 1,3±0,7 |
Au | 1,25 | 1,5±0,3 |
Pb | 0,25 | 0,19±0,02 |
Al | 1,08 | 2,2±0,7 |
Как видно из Таблицы 1, рассчитанные значения сопротивления, обусловленного рассеянием на вакансиях, находятся в неплохом согласии с экспериментальными данными. Результаты измерений вакансионного вклада в сопротивление металлов имеют довольно большой разброс, что, возможно, связано с отличиями в оценке числа вакансий и условиях закалки в различных экспериментах.
Имеющееся согласие экспериментальных и расчетных значений позволяет по величине полного прироста сопротивления закаленного металла и вычисленному по формуле (33) значению сопротивления на один атомный процент вакансий оценить концентрацию вакансий в металле. Это представляет определенный практический интерес ввиду сравнительной простаты данного метода в сравнении с другими возможными способами определения концентрации вакансий в металлах.
5. Заключение
За счет вакансий для неупорядоченных и частично упорядоченных сплавов происходит увеличение остаточного электросопротивления при любых составах и значениях параметра дальнего порядка.
В неупорядоченных изоэлектронных сплавах вакансионный вклад в сопротивление, приходящийся на один атомный процент вакансий, не зависит от состава сплава.
Численные оценки обусловленного одним атомным процентом вакансий вклада в электросопротивление чистых металлов находятся в хорошем согласии с экспериментальными значениями для целого ряда металлов (Cu, Ag, Au, Pb, Al), что позволяет весьма надежно оценивать концентрацию вакансий в металле по величине полного прироста сопротивления закаленного металла.
