MODELLING OF PROPAGATION OF STRONG PERTURBATIONS IN GAS OF ARBITRARY RAREFACTION

Одной из популярных областей, где используются численные методы, является изучение быстропротекающих процессов в сильно возмущенной газообразной среде.

В большинстве случаев применяют численные схемы с методом Монте-Карло, где реальный газ заменяется системой большого числа частиц, которые на каждом временном шаге всегда имеют вполне определенные координаты и скорости, перемещаются на некоторое расстояние в пространстве и совершают определенное количество столкновений между собой. Недостатком данного метода является слишком высокая требовательность к вычислительным ресурсам, связанная с необходимостью переработки большого объема информации о рассматриваемой системе, которая является излишней при вычислении макроскопических средних параметров.

Однако более последовательным подходом является применение кинетической теории газов, которая изучает свойства газов методами статистической физики на основе представлений об их молекулярном строении и определенных законах взаимодействия между молекулами. В этом случае необходимо решать нестационарное кинетическое уравнение Больцмана с помощью различных численных методов, которые позволяют получить довольно точные результаты, описывающие поведение газа в некотором объеме с течением времени.

Решению именно этого уравнения была посвящена данная работа, целью которой являлось изучение распространения сильных возмущений температуры и плотности в газе произвольной разреженности с помощью решения уравнения Больцмана методом дискретных скоростей.

Состояние любого газа можно описать одночастичной функцией распределения , которая позволяет найти в момент времени  долю частиц, находящихся в единице объема, в заданном интервале скоростей. Для определения этой функции Л. Больцман в 1872 году получил интегро-дифференциальное уравнение

(1.1)

где  – функция распределения, которая зависит от координат N-мерного пространства , скорости частицы  и времени t;

  – скорость частицы в пространстве;

 – поле внешних сил, действующих на частицу в жидкости или газе;

J – интеграл столкновений – выражение, учитывающее влияние столкновений частиц или молекул.

Однако в данной работе полем внешних сил будем пренебрегать, поскольку рассматриваются сильные возмущения, а значит, скорости частиц будут настолько велики, что внешние силы не успеют оказать никакого воздействия на систему в течение рассматриваемого времени.

В кинетической теории газов одной из популярных моделей столкновений для уравнения Больцмана является модель Бхатнагара-Гросса-Крука (БГК), которая заключается в том, что интеграл столкновений имеет следующий вид

(1.2)

где  – локально-равновесная функция распределения, к которой стремится искомая функция распределения  за счет столкновений частиц;

(1.3)

где  – постоянный коэффициент, который определяется экспериментальным путем. В данной работе рассматривается модель твердых сфер, а значит, ;

 – динамическая вязкость при эталонной температуре 

Для модели БГК локально-равновесная функция распределения  определяется выражением

(1.4)

где n – числовая плотность или концентрация частиц, 1/м3;

m – масса молекулы газа, кг;

M – молярная масса газа, кг/моль;

R = 8,31 Дж/(моль*K) – универсальная газовая постоянная;

T – температура газа, К

  – вектор скорости частицы относительно скорости движения газового потока, так называемая тепловая скорость молекулы;

u – вектор средней скорости газового потока.

Для удобства решения уравнения Больцмана воспользуемся методом подобий и обезразмерим переменные. Для этого положим, что на бесконечном удалении от точки или границы возмущения, газ находится в равновесии и не возмущен, тогда его состояние описывается максвелловской функцией распределения

(1.5)

где  – числовая плотность и температура находящегося в равновесии невозмущенного газа, соответственно.

Введем масштабные параметры:

(1.6)

В формулах (1.6) характеристическая скорость  и время   определяются как:

(1.7)

где  – характерная длина задачи.

Тогда получим следующие выражения для равновесных функций распределения:

(1.8)

(1.9)

Также обезразмерим давление и выразим ее через числовую плотность и температуру, записав уравнение идеального газа:

(1.10)

После подстановки получим безразмерное уравнение Больцмана:

(1.11)

где  – параметр, обратный числу Кнудсена, который характеризует роль столкновений в рассматриваемой задаче.

Скорость частицы  является непрерывной величиной в пространстве фазовых скоростей, а её абсолютная величина изменяется от 0 до  Однако в практических расчетах, согласно рассматриваемому методу, пространство скоростей должно разбиваться на набор дискретных значений . При этом для каждой группы частиц со скоростями  записывается основное уравнение Больцмана

(1.12)

где  – дискретная функция распределения вдоль направления скорости .

Для простоты записи формул вместо  будем использовать обозначение . Проинтегрируем уравнение (1.12) вдоль траектории молекул со скоростью  за один временной шаг , а также воспользуемся методом трапеций для интегрирования члена столкновений. Тогда получим следующее выражение:

(1.13)

где  – координата центра ячейки;

 – член, учитывающий столкновения частиц.

Также обратим внимание на то, что уравнение (1.13) является неявным из-за включения члена столкновений , а именно, из-за того, что в левой и правой его части содержится искомая функция . Чтобы устранить это, перейдем к некоторой функции распределения , которая определяется следующим выражением:

(1.14)

Подставив преобразование (1.14) в уравнение (1.13), получим:

(1.15)

В уравнении (1.15)  – это масштаб времени релаксации газовой системы в центре ячейки в момент времени .

Будем считать, что макропараметры рассматриваемой системы мало изменяются на расстояниях порядка средней длины свободного пробега молекул. В этом случае состояние газа в расчетной области близко к равновесному и описывается следующим выражением с помощью некоторой функции возмущения 

(1.16)

где  – равновесная максвелловская функция распределения для дискретного значения скорости которая вычисляется по формуле (1.5).

Подставим (1.16) в (1.15), получим следующее выражение: 

(1.17)

Уравнение (1.17) легко решается с помощью процессов потоковой передачи (перелетов без столкновений) в рассматриваемой среде и столкновений, происходящих в ней:

1) При  столкновений нет, а, следовательно, шаг потоковой передачи будет равняться:

(1.18)

2) Подставив (1.18) в (1.17), получим так называемый шаг столкновений:

(1.19)

где  – функция возмущения в центре ячейки на следующем временном шаге при отсутствии столкновений для дискретного значения скорости .

Таким образом, чтобы найти функцию возмущения  от момента времени  до  необходимо заранее определить .

 – это функция возмущения в точках, окружающих центр ячейки в текущий момент времени, которая вычисляется с помощью методов интерполяции. В данной работе для её поиска используются функция возмущения  и ее производные первого порядка в центре ячейки, которые возникают при разложении рассматриваемой функции в ряд:

(1.20)

В приведенном выше уравнении (1.20) ключевым моментом является вычисление градиента функции возмущения  в центре ячейки. Для его нахождения применяют метод Грина-Гаусса, согласно которому градиент  в центре ячейки I можно выразить следующим образом:

(1.21)

где  – объем ячейки I;

 – число ячеек J, которые граничат с ячейкой I;

 – индекс, который обозначает клетки, граничащие с ячейкой I;

 – функция возмущения на границе ячейки I, внешний единичный вектор нормали и площадь границы раздела ячейки I и ячейки J, соответственно.

Как видно из уравнения (1.21), ключом к вычислению градиента  является восстановление функции возмущения на границе ячейки . Для этой цели в работе применяется метод MUSCL, который представляет собой метод конечных объемов и может обеспечить высокоточные численные решения для рассматриваемой системы. При этом используется ограничитель Бергер, который позволяет устранить нефизические колебания, связанные с резким и внезапным изменением найденных величин вблизи фронта возникающей ударной волны

Для вычисления локально-равновесной функции возмущения  необходимо оценить макропараметры на следующем временном шаге в центре ячейки. В данной работе для этой цели используется линейная экстраполяция:

(1.22)

(1.23)

(1.24)

где  – безразмерные числовая плотность, вектор средней скорости потока и температура на предыдущем шаге по времени.

Вычислив  можно найти локально-равновесную функцию возмущения  по следующей формуле, воспользовавшись выражениями (1.8), (1.9) и (1.16): 

(1.25)

Теперь для удобства решения рассматриваемой задачи введем следующие обозначения:

(1.26)

Подставим (1.26) в уравнение (1.17), получим: 

(1.27)

В процессе локальной реконструкции функции возмущения в точках, окружающих центр каждой ячейки используется шаг по времени . Принцип выбора заключается в том, что максимальная длина свободного пробега в ячейке  должна быть меньше половины размера ячейки

(1.28)

где  — вектор максимальной дискретной скорости;

 — вектор минимального шага сетки.

Уравнение (1.28) также можно записать в виде условия сходимости Куранта-Фридрихса-Леви, которое является необходимым условием сходимости при численном решении некоторых уравнений в частных производных. Оно возникает при численном анализе явных схем интегрирования по времени, когда они используются для решения рассматриваемой задачи. Как следствие, при численном решении нестационарных задач шаг по времени должен быть меньше определенного времени, в противном случае моделирование дает неправильные результаты из-за расходимости искомых величин

(1.29)

где  – коэффициент Куранта-Фридрихса-Леви, который должен быть меньше. В данной работе для всех моделей используется  = 0,45.

Обезразмерим рассматриваемый интервал времени , используя масштабное время (1.7):

(1.30)

Было показано, что  можно вычислить с помощью формулы (1.6). Тогда получим следующее выражение для члена, входящего в уравнение (1.17): 

(1.31)

где  – параметр, обратный числу Кнудсена, при условии, что газ находится в равновесии и считается невозмущенным.

Подставим (1.31) в (1.26), получим следующие выражения:

(1.32)

Теперь подставим (1.16) и (1.31) в (1.14) и получим окончательное выражение для поиска функции возмущения  в центре ячейки на следующем временном шаге:

(1.33)

В итоге принципиальная схема метода дискретных скоростей показана на рисунке 1.

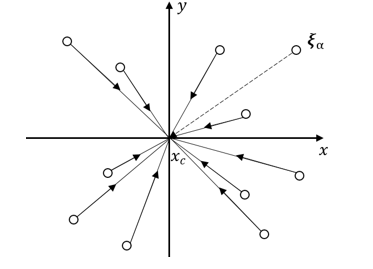
Рисунок 1 - Схема метода дискретных скоростей в двумерном случае

DOI:10.60797/IRJ.2024.143.150.1

Как видно из этого рисунка и уравнений (1.27) и (1.33), для поиска функции возмущения  необходимо рассчитать только функцию возмущения  в точках, окружающих центр ячейки в текущий момент времени, и локально-равновесную функцию возмущения на следующем временном шаге  Как только они будут получены, мы можем вычислить промежуточные функции возмущения в центре ячейки  с помощью потокового процесса (1.18) и переместить функции возмущения на следующий временной шаг с помощью шага столкновений (1.27). Таким образом, сделав обратное преобразование (1.33) и вычислив ,  можно рассчитать искомые функции распределения  а следовательно, и интересующие макропараметры, при этом необходимо просуммировать найденные функции распределения по всем рассматриваемым скоростям. Покажем это, записав формулы для исследуемых макропараметров.

Далее все переменные будут обезразмерены, но для простоты индекс безразмерных величин будет опущен. Также в данной работе рассматривается цилиндрическая система координат, тогда вектор скорости имеет вид 

Из формулировки функции распределения  следует, что величина

(1.34)

характеризует среднее число частиц, находящихся в момент времени  в единице объема около центра рассматриваемой ячейки с радиус-вектором .

Из кинетической теории газов известно, что среднее значение любой функции , зависящей от скорости, можно вычислить по следующей формуле: 

(1.35)

Тогда составляющие макроскопической средней скорости газового потока  вычисляются по формулам (1.36) и (1.37). Опустим запись аргумента у подынтегральной функции, чтобы уменьшить размер выражений:

(1.36)

Аналогичное выражение получим для :

(1.37)

Составляющей средней скорости газового потока по азимутальному направлению  пренебрегаем, поскольку рассматриваемая система не вращается, а также наблюдается симметрия по азимутальному углу 

Перейдем к вычислению температуры. По определению температура газа – это средняя кинетическая энергия теплового движения молекул. К тому же в работе в качестве рабочего газа рассматривается одноатомный газ, следовательно, вращательные и колебательные степени свободы будут отсутствовать. Запишем формулу для кинетической энергии теплового движения молекул: 

(1.38)

Обезразмерим записанное выражение при помощи (1.6) и (1.7): 

(1.39)

Сократим, опустим индекс обезразмеривания и применим формулу (1.35). В итоге получим окончательное выражение для вычисления температуры газа:

(1.40)

Для вычисления функции возмущения   в точках, окружающих центр ячейки в текущий момент времени, необходимо разложить ее в ряд, согласно выражению (1.20). Распишем градиент функции возмущения  и раскроем скалярное произведение:

(1.41)

Чтобы вычислить соответствующие частные производные, необходимо восстановить значения функции возмущения на границах ячейки. Для этого в данной работе используется метод MUSCL (Monotonic Upstream-centered Scheme for Conservations Laws) так называемая монотонная схема законов сохранения, ориентированная на восходящий поток

[10]

,

[11]

. Изобразим графически суть данного метода и вычислим значение производной по радиусу, начиная от стенки расчетной области для молекул, летящих от нее (см. рис. 2).

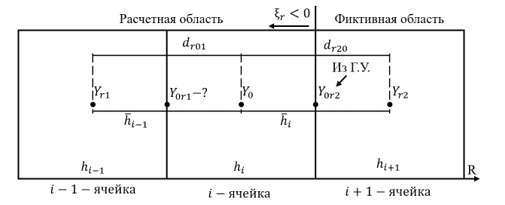
Рисунок 2 - Графическая интерпретация метода MUSCL

DOI:10.60797/IRJ.2024.143.150.2

Сначала рассчитаем шаги и разности значений функций возмущений между центрами ячеек:

(1.42)

(1.43)

Зная  в текущий момент времени, которые были рассчитаны на предыдущем временном шаге, и  из граничных условий, найдем значение функции возмущения  на границе ячейки

(1.44)

где  – ограничитель наклона градиента Бергер, который играет ключевую роль в уменьшении общей дисперсии найденных значений и позволяет повысить точность численных методов, а также устранить нефизические колебания, связанные с резким и внезапным изменением найденных величин вблизи фронта ударной волны.

 – малое число в аргументе, которое позволяет предотвратить деление на ноль в области нулевого градиента.

В итоге, вычислив значение на границе ячейки, найдем компоненту градиента функции возмущения по радиусу: 

(1.45)

Аналогичная формула для частной производной по радиусу получится, если молекулы движутся в расчетной области слева направо [10]. В этом случае мы находим правую границу ячейки  

(1.46)

Выражения для частных производных по высоте  и азимутальному углу  имеют подобный вид, меняются лишь индексы у границ ячейки и разностей функций возмущений.

Перейдем к вычислению ограничителя Бергер  который вычисляется с помощью следующих выражений [10, 12]. Сначала определяются коэффициенты растяжения сетки: 

(1.47)

Затем вычисляются индикатор местоположения , показывающий относительное расположение  между  и , и граница  между двумя областями TVD (Total Variation Diminishing), в которых восстанавливается значение функции возмущения и обеспечивается стабильность и точность применяемого численного метода за счет использования ограничителей наклона градиента и уменьшения общей дисперсии найденных величин:

(1.48)

Тогда ограничитель Бергер , который уже зависит от индикатора местоположения , можно вычислить по следующей формуле

(1.49)

Таким образом, функция  ограничивает наклон градиента и проходит через специальную область TVD решения, где обеспечивается стабильность и точность применяемого численного метода при описании физических процессов, в которых могут наблюдаться скачки и разрывы исследуемых параметров.     

В данной работе используется два типа граничных условий, первым из которых является свободная проницаемая поверхность, где рабочий газ контактирует с газом, имеющим фиксированную плотность и температуру. Вторым типом является изотермическая непроницаемая стенка, для которой предполагается идеальное диффузное отражение.

Рассмотрим первый тип граничных условий, согласно которому граница представляет собой газ, находящийся при определенной температуре  и плотности  Таким образом, зная макропараметры стенки, можно найти функцию возмущения на ней с помощью выражения (1.25), при этом средняя скорость газового потока равна нулю, поскольку поверхность считается неподвижной: 

(1.50)

где  – центр ячейки соответствующей поверхности, на которой задается данный тип граничных условий.

Перейдем ко второму типу граничных условий, а именно, к непроницаемой изотермической стенке с идеальным диффузным отражением. Поскольку решение последующих задач будет производиться в цилиндрической системе координат, выведем формулу для нижней стенки, которая имеет температуру  Запишем выражение для функции распределения с помощью (1.9), зная, что молекулы, которые попадают на стенку, отражаются с максвелловской функцией распределения:

(1.51)

где  – радиус-вектор центра ячейки на нижней поверхности; 

  – числовая плотность молекул, отраженных от нижней поверхности.

Поскольку нижняя стенка непроницаемая, следовательно, плотность потока молекул газа через нее равна нулю. Запишем это, воспользовавшись выражением (1.36):

(1.52)

где  – плотность потока падающих на нижнюю поверхность молекул, находящихся в равновесном состоянии;

 – плотность потока падающих молекул, которые подверглись возмущению  вблизи нижней стенки;

 – средняя скорость молекул, отраженных от нижней стенки.

Тогда выражение для числовой плотности  будет иметь следующий вид: 

(1.53)

Выражения для верхней и боковой поверхностей выводятся аналогичным образом, меняется лишь направление полета падающих и отраженных молекул.

Таким образом, зная температуры поверхностей, на которых задаются граничные условия, можно вычислить числовые плотности отраженных от них молекул, а также найти функции возмущения по формуле (1.50). Вычисленные функции возмущения будут использоваться в методе MUSCL для восстановления значений на границах ячеек, что было показано ранее.

Для проверки предложенной схемы метода дискретных скоростей и метода MUSCL с ограничителем наклона градиента Бергер было принято решение смоделировать ударные волны, поскольку именно в них наблюдаются резкие скачки макропараметров газа, которые могут влиять на сходимость численного решения. С этой целью была решена задача моделирования распада первоначально заданного разрыва макропараметров покоящегося газа в ударной трубке Сода

Таким образом, задаются следующие кусочно-постоянные начальные условия

(1.54)

где  – числовая плотность, средняя скорость газового потока и температура в i-ой части расчетной области, соответственно.

В итоге начальное распределение макропараметров газа по высоте цилиндра имеет следующий вид (см. рис. 3). 

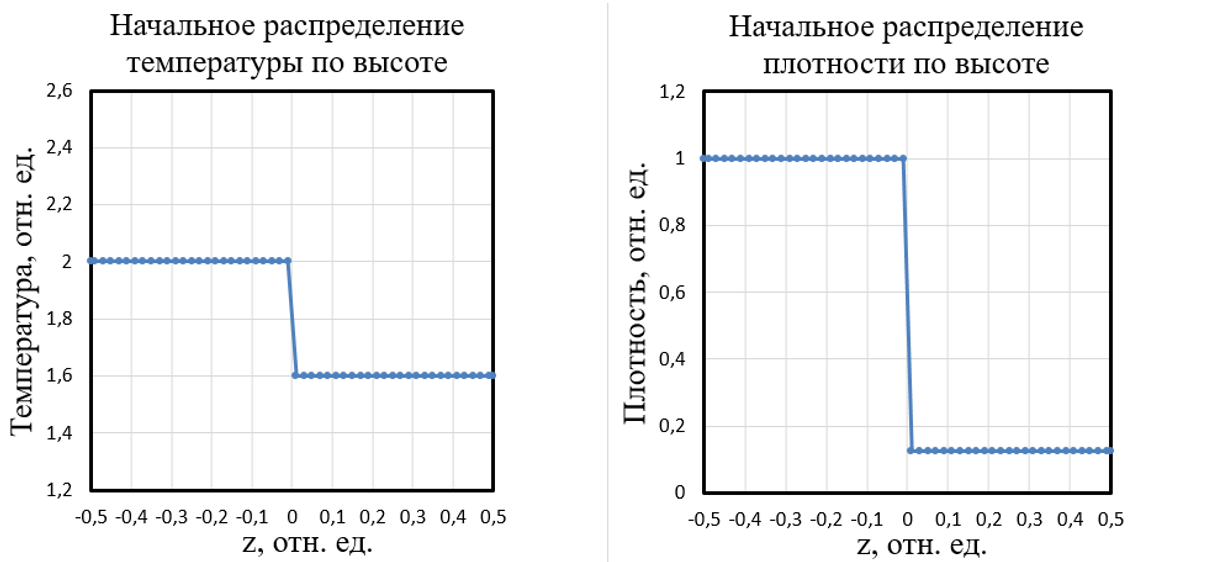
Рисунок 3 - Начальное распределение температуры и концентрации по высоте цилиндра

DOI:10.60797/IRJ.2024.143.150.3

При моделировании, как отмечалось ранее, используется цилиндрическая система координат. При этом исследуемый интервал скоростей разделяется на 40 значений, сетка по радиусу – на 11 ячеек, по высоте цилиндра – на 101 ячейку, по азимуту – на 11 ячеек и по полярному углу в пространстве скоростей на 20 ячеек. Причем первая и последняя ячейки по высоте и последняя ячейка по радиусу представляют некоторую фиктивную расчетную область цилиндра, где задаются граничные условия.

Также стоит обсудить полярный угол, который вводится в данной работе впервые. Поскольку в методе дискретных скоростей рассматривается дискретный ряд абсолютных значений вектора скорости , то для нахождения проекций этой скорости вводится сферическая система координат. Тогда: 

(1.55)

(1.56)

(1.57)

Таким образом, найденные проекции скорости, будут использоваться для вычисления интегралов в выражениях (1.34) – (1.40) при вычислении макропараметров газа и в формулах (1.51) – (1.53) при определении плотности потока газа через границы расчетной области.

Для решения задачи ударной трубки Сода в качестве граничных условий были выбраны следующие: нижняя стенка представляла собой изотермическую непроницаемую поверхность с идеальным диффузным отражением, а верхняя и боковая стенки являлись свободными проницаемыми поверхностями. В итоге расчетная область в начальный момент времени будет иметь следующий вид, который показан на рисунке 4.

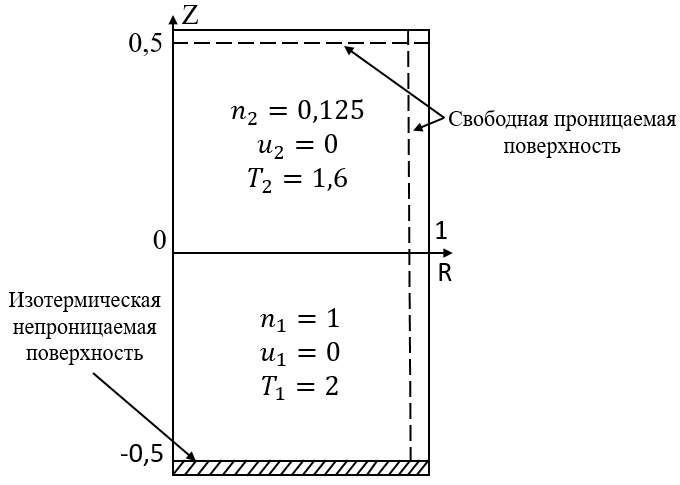
Рисунок 4 - Схема расчетной области в начальный момент времени при решении задачи ударной трубки Сода

DOI:10.60797/IRJ.2024.143.150.4

Таким образом, после задания всех необходимых граничных и начальных условий, была запущена программа расчета. Вначале исследовалось течение разреженного газа и проводился последующий анализ полученных результатов, при этом значение числа Кнудсена составило Kn = 18,05. В итоге по окончании расчета были получены следующие распределения температуры и числовой плотности по высоте цилиндра для свободномолекулярного режима течения, изображенные на рисунке 5, которые были соотнесены с теоретическими значениями

[4]

,

[17]

,

[18]

.

Перейдем к анализу полученных результатов. Как мы видим на графике температур, в расчетном объеме возникает три характерных области. Поскольку газ является разреженным, то первая область – это фронт слабой ударной волны, который образуется, когда происходит разрыв диафрагмы и рабочий газ под высоким давлением устремляется в область низкого давления, тем самым сжимая исследуемый газ и увеличивая его температуру, числовую плотность и давление.

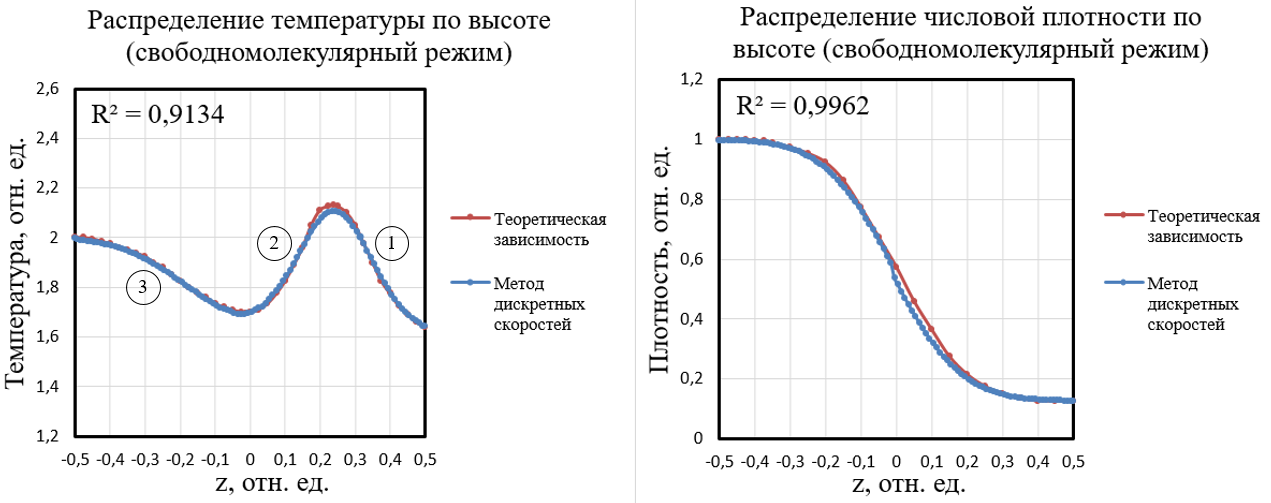
Рисунок 5 - Распределение температуры (слева) и числовой плотности (справа) по высоте цилиндра в ударной трубке Сода для свободномолекулярного режима течения при Kn = 18,05 (δ0 = 0,0554) в момент времени t = 0,16

DOI:10.60797/IRJ.2024.143.150.5

Вторая область – это область распространения контактной поверхности, которая движется со скоростью меньшей скорости звука и не может догнать фронт ударной волны.

Третья область – это область волн разрежения, которые распространяются в противоположном направлении от ударной волны по рабочему газу, уменьшая непрерывно и равномерно значения его макропараметров.

Однако, как мы видим, характерных областей на рисунке 5 для распределения числовой плотности не возникает. Это связано с тем, что для разреженного газа длина свободного пробега молекул много больше характерного размера задачи и образующийся из-за этого утолщенный фронт слабой ударной волны практически никак не влияет на резкое изменение плотности, а непрерывно и равномерно увеличивает её.

Затем изучался промежуточный режим течения, при этом значение числа Кнудсена составило Kn = 0,001805  . В итоге по окончании расчета были получены следующие распределения температуры и числовой плотности по высоте цилиндра, изображенные на рисунке 6, которые были соотнесены с теоретическими значениями

Для промежуточного режима течения образуются аналогичные характерные области. Однако эти же области начинают проявляться на графике для числовой плотности, поскольку в промежуточном режиме течения длина свободного пробега молекул меньше характерного размера задачи или сопоставима с ним. Тогда толщина фронта образующейся ударной волны становится меньше, а значит, вследствие этого возникает скачкообразное изменение плотности при сжатии исследуемого газа, что видно на рисунке 6 для числовой плотности. Аналогичные рассуждения справедливы для обоснования уменьшения толщины контактной поверхности при снижении разреженности среды. Это отчетливо видно при сравнении распределений, изображенных на рисунках 5 и 6.

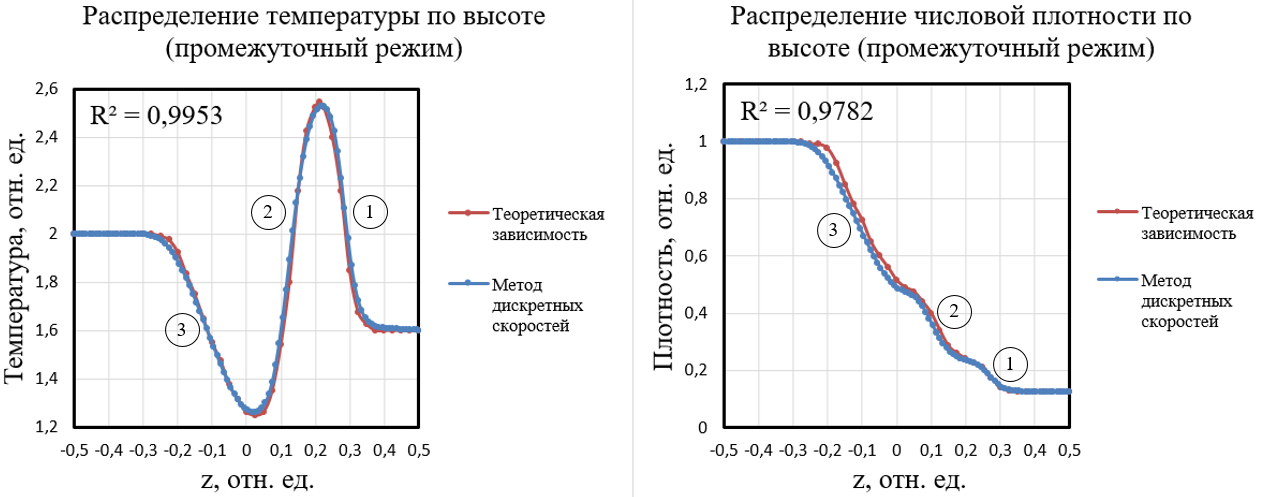
Рисунок 6 - Распределение температуры (слева) и числовой плотности (справа) по высоте цилиндра в ударной трубке Сода для промежуточного режима течения при Kn = 0,001805 в момент времени t = 0,16

DOI:10.60797/IRJ.2024.143.150.6

На полученных распределениях для разреженного и промежуточного режимов течения есть небольшие расхождения в некоторых областях, которые связаны с небольшим разбиением расчетной области из-за недостаточных вычислительных мощностей персональных компьютеров, на которых производились расчеты. Однако на рассматриваемых графиках 5 и 6 наблюдаются количественные совпадения кривых. Это подтверждается рассчитанным коэффициентом детерминации, который на всех графиках превышает значение 0,9, а в некоторых случаях стремится к единице. Таким образом, это свидетельствует о том, что метод дискретных скоростей позволяет решить кинетическое уравнение Больцмана в приближении БГК и получить результаты достаточно близкие к теоретическим.

В заключение стоит отметить, что применение численных методов к кинетической теории газов в данной работе, а именно: метода дискретных скоростей и метода MUSCL с ограничителем наклона градиента Бергер при решении уравнения Больцмана позволяют не только рассчитать макропараметры газа и изучить изменение их полей, но и смоделировать быстропротекающие процессы в сильно возмущенном газе произвольной разреженности, одним из которых является распространение фронта ударной волны.