VACANCY MIGRATION OF CATIONS IN URANIUM DIOXIDE. А MOLECULAR DYNAMICS SIMULATION
VACANCY MIGRATION OF CATIONS IN URANIUM DIOXIDE. А MOLECULAR DYNAMICS SIMULATION
Abstract
A model is proposed that describes the behavior of a uranium dioxide crystal with a point defect, based on the molecular dynamics method. The model system was a face-centered cubic crystallite of 765 particles with a vacancy-type point defect. Boundary conditions were maintained through the use of a Berendsen thermostat. The purpose of the simulation was to study the migration of vacancies and cations inside the crystal at different temperatures.
Migration of cations was analyzed based on the dependence of the logarithm of the diffusion coefficient of cations on the reciprocal temperature of the crystal lattice, which was constructed using the known relationship between the diffusion coefficient and the mean square displacement of atoms in the crystal. An effective diffusion activation energy of 1.10 eV was obtained, which is close to the experimental and calculated data of other authors for a single cation vacancy, which is in the range of 1.5-3.0 eV. The somewhat underestimated result can be explained by the presence of two anion vacancies next to the cation vacancy, which reduced the mobility of the vacancy cluster.
1. Введение
Диоксид урана UO2 широко используется в качестве топлива для ядерной энергетики. Такие его свойства, как отсутствие фазовых переходов и взаимодействия с цирконием, ниобием, нержавеющей сталью при высоких температурах, позволяют эффективно применять его в ядерных реакторах, получая высокий КПД. Этими факторами и обусловлен выбор диоксида урана в качестве исследуемого модельного вещества. Диоксид урана, как и другие оксиды урана, используется также как промежуточный продукт при производстве других урановых соединений, главным образом фторидов. Все оксиды урана являются наиболее устойчивыми его соединениями, в связи с чем широко используются как для хранения урана, так и как промежуточное звено между урановорудным и фторидными урановыми производствами.
Точечные дефекты в кристаллических решетках твердых веществ играют важную роль в миграции атомов. Они влияют на механические свойства материала, его проводимость, подвижность носителей заряда и др. Образование и миграция дефектов типа «вакансия» напрямую связано с явлением самодиффузии веществ
. Изучение миграции дефектов в кристаллах представляется возможным с помощью моделей, созданных и исследуемых на ЭВМ и основанных на методе молекулярной динамики (МД). Взаимодействие частиц достаточно просто описывается МД, но увеличение размеров исследуемого кристаллита значительно усложняет расчет требуемых характеристик в связи с огромным количеством вычислительных задач. Рост объема вычислений, связанный с усложнением задач, решаемых с помощью ЭВМ в военной, технологической, научной и финансовой областях, привел к созданию мощных суперкомпьютеров и их более дешевых заменителей, многопроцессорных вычислительных комплексов.Создание модели физических объектов в большей степени помогает избавиться от лишних временных, финансовых или кадровых затрат на изучение самого объекта. Понимание основных характеристик и функций объекта, цель исследования, а также корректная расстановка приоритетов между исследуемыми процессами деятельности объекта помогает создать оптимальную по всем пунктам модель. В нашей работе такой моделью является компьютерная программа, описывающая поведение множества материальных точек, связанных между собой физическими законами. Объектом, по которой построена модель, является трехмерная кристаллическая решетка диоксида урана. Удалив из модели одну или более специальным образом выбранные точки, можно получить аналог такого физического явления, как образование точечного дефекта в кристалле твердого тела вакансионного типа. Необходимая производительность вычислений достигнута с использованием программно-аппаратной платформы CUDA компании NVIDIA, обеспечившей возможность организации доступа к набору инструкций графического ускорителя и управления его памятью при организации параллельных вычислений
, .2. Метод молекулярной динамики
В основе метода молекулярной динамики (МД) лежит модельное представление о многоатомной молекулярной системе, в которой все атомы представлены материальными точками, движение которых описывается в классическом случае уравнениями Ньютона . Таким образом, имеется N точечных частиц, каждая из которых
1) имеет массу, радиус-вектор и скорость соответственно ,
,
, где
,
2) взаимодействует с остальными посредством сил , где
потенциальная энергия взаимодействия системы из N частиц,
3) взаимодействует с внешними полями посредством силы .
Тогда эволюция данной модели будет описываться системой 2N обыкновенных дифференциальных уравнений движения.
В работе задействуется один из наиболее используемых потенциалов в методе молекулярной динамики – потенциал Букингема:
Потенциал (1) описывает отталкивание электронных оболочек в экспоненциальной форме, которая является наиболее теоретически обоснованной из простых функциональных зависимостей. Он не учитывает затухания дисперсионного притяжения на малых расстояниях порядка суммы радиусов взаимодействующих частиц, на которых не справедливо мультипольное разложение .
3. Принципы моделирования ионных кристаллов методом молекулярной динамики
Заключается алгоритм МД в том, что кристалл представляется системой недеформируемых, положительных и отрицательных, ионов, эволюционирующей во времени. Ионы перемещаются по законам Ньютона, а силы взаимодействия определяются парными потенциалами Uij(Rij)
.Потенциалы Uij(Rij) имеют общий вид
где QiQj – заряды i-го и j-го ионов;
Rij – расстояние между этими ионами;
KE – константа закона Кулона;
UijОб (Rij) – некулоновский потенциал взаимодействия электронных оболочек (1).
Потенциалы UijОб (Rij) представляют в различных формах, обычно включающих в себя слагаемые, моделирующие отталкивание перекрывающихся электронных оболочек на малых расстояниях и дисперсионное притяжение на сравнительно больших. Наиболее известными из этих форм являются потенциал Букингема (1) и потенциал Леннарда-Джонса.
В формуле (1) А и В – константы, характеризующие отталкивание оболочек, C6, C8 – константы, описывающие дипольную и квадрупольную составляющие дисперсионного притяжения.
Перед началом расчёта ионам присваиваются некоторые начальные координаты и скорости (например – координаты, соответствующие узлам идеальной кристаллической решётки моделируемого соединения и скорости, соответствующие Максвелловскому распределению при заданной температуре), после чего начинается численное пошаговое интегрирование уравнений движения ионов во времени. На каждом k-ом шаге производятся следующие действия:
1) рассчитываются действующие на каждый ион силы
2) вычисляются новые скорости и новые координаты ионов
Формулы (3-5) справедливы при нулевых граничных условиях (конечный кристаллит из N частиц в вакууме) без компенсации перемещения, вращения и дрейфа температуры, возникающих из-за вычислительных погрешностей (алгоритмы компенсации приведены ниже). Однако этих формул достаточно, чтобы показать возможность эффективного распараллеливания по схеме SIMD: очевидно, что основные этапы алгоритма заключаются в проведении над каждым из ионов поочерёдно одних и тех же операций.
Наиболее критичным участком алгоритма является расчёт результирующих сил, действующих на каждый из ионов со стороны остальных. Этот расчёт необходим на каждом шаге молекулярной динамики, а его объём квадратичен по количеству частиц N, так как для каждой из N частиц необходимо выполнить суммирование сил, действующих со стороны N-1 остальных:
Поскольку для реалистичного моделирования модельные кристаллиты должны содержать десятки и сотни тысяч ионов, объём расчёта (6) очень велик по сравнению с расчётами на остальных этапах алгоритма. Именно этот расчёт имеет смысл в первую очередь реализовать на графических процессорах. Нам такая реализация позволила на порядки ускорить молекулярно-динамическое моделирование ионных кристаллов (диоксида урана) .
4. Миграция точечных дефектов
В какой-то момент атом может получить от соседей такой избыток энергии, что он займёт соседнее положение в решётке. Так осуществляется миграция (перемещение) точечных дефектов в объёме кристаллов .
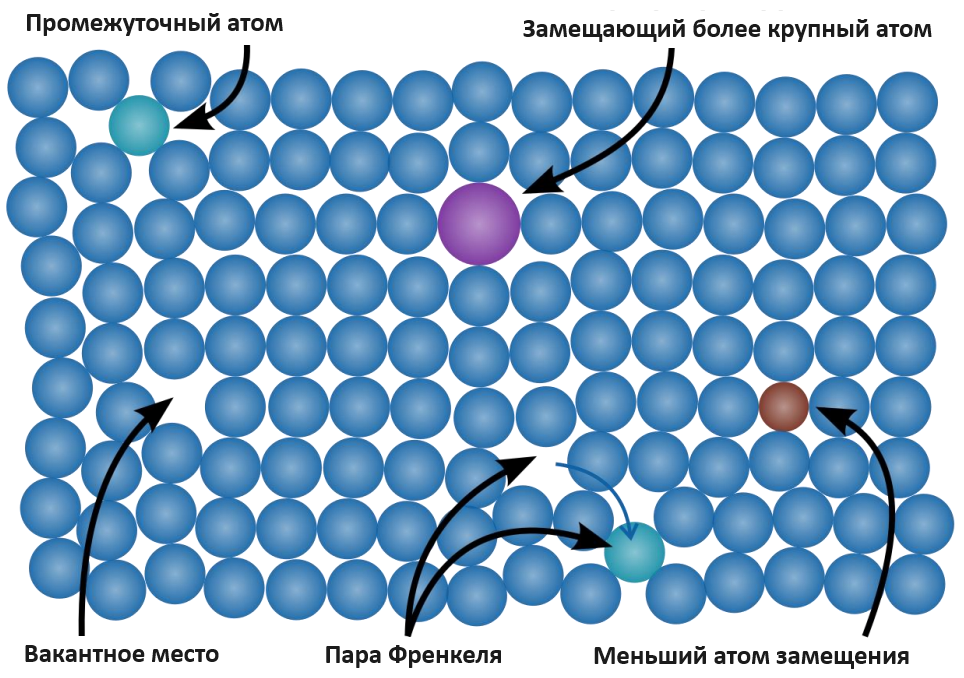
Рисунок 1 - Точечные дефекты
Примечание: по ист. [7]
5. Моделирование кристаллической решетки с вакансией. Миграция катионов. Диоксид урана
Моделирование миграции катионов в настоящей работе включало следующие этапы:
1) создание модель кристаллической решетки диоксида урана;
2) удаление одной молекулы UO2 из решетки диоксида урана для формирования вакансии;
3) моделирование поведение кристаллической решетки в течение некоторого интервала времени,
Кристаллическая решетка диоксида урана имеет гранецентрированную кубическую форму. Теоретическая плотность – 10,96 г/см3, температура плавления 2875±45 °С
, .В качестве исследуемой модели используется нанокристалл кубической формы размером 22×22×22 Å (ангстрем), содержащий 256 атомов 92238U и 512 атомов 816O (всего 768 атомов) (рисунок 2). Потенциалом взаимодействия выбран потенциал Букингема (1), дополненный слагаемым, характеризующим кулоновское отталкивание частиц (2).
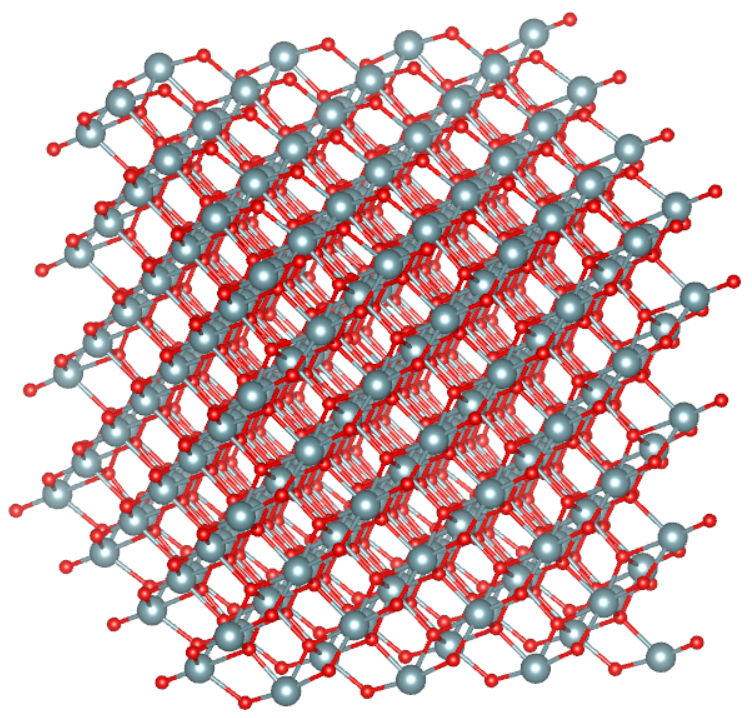
Рисунок 2 - Кристаллическая решетка диоксида урана в начальный момент времени:
серые большие шары – атомы урана; красные меньшие – атомы кислорода
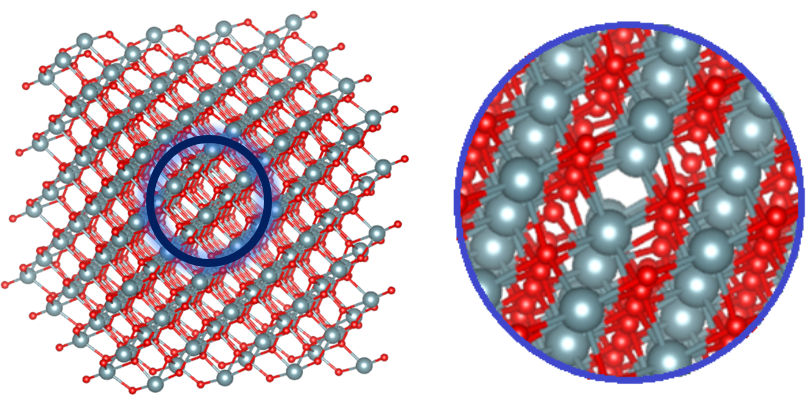
Рисунок 3 - Наглядное изображение вакансии внутри кристаллической решетки
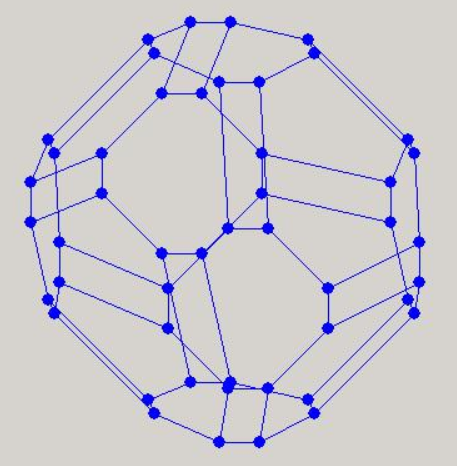
Рисунок 4 - Пример координационной сферы
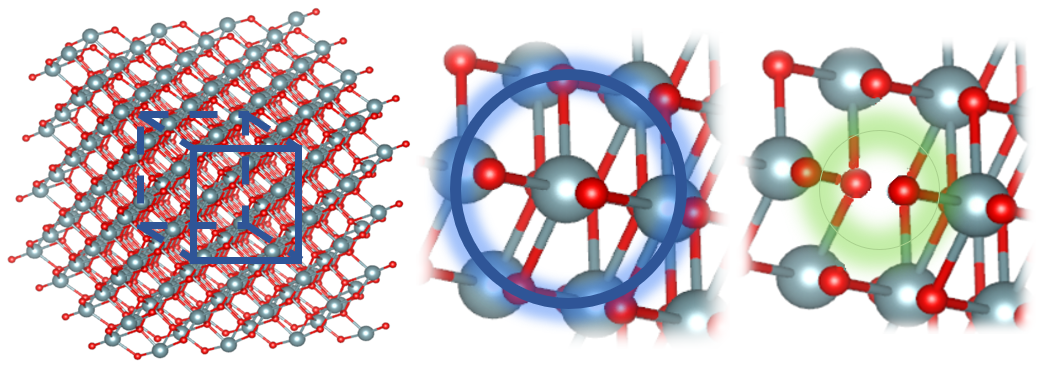
Рисунок 5 - Метод регистрации катионной вакансии
6. Анализ результатов моделирования
В первую очередь необходимо установить наличие вакансии в кристалле вышеприведенным методом и оценить факт ее перемещения внутри кристалла с течением времени. По истечении времени моделирования были получены координаты как самих атомов урана и кислорода, так и координаты вакансии в каждый момент времени. На Рисунке 6 приведен вид кристаллической решетки в последний момент времени расчета, где фиолетовой сферой обозначено местоположение катионной вакансии.
Таким образом, факт нахождения самой вакансии в кристалле подтвержден. Далее следует установить наличие миграций данной вакансии и катионов внутри кристалла с течением времени. Для этого вычисляли квадрат смещения σ2 вакансии и атомов вокруг нее относительно их начального положения в каждый момент времени:
где X0, Y0, Z0 – начальные координаты вакансии и катионов;
Xi, Yi, Zi – координаты вакансии и катионов в текущий момент времени.
Получив нужные значения, строили график зависимости квадрата смещения вакансии от номера итерации для двух значений температур (Рисунок 7).
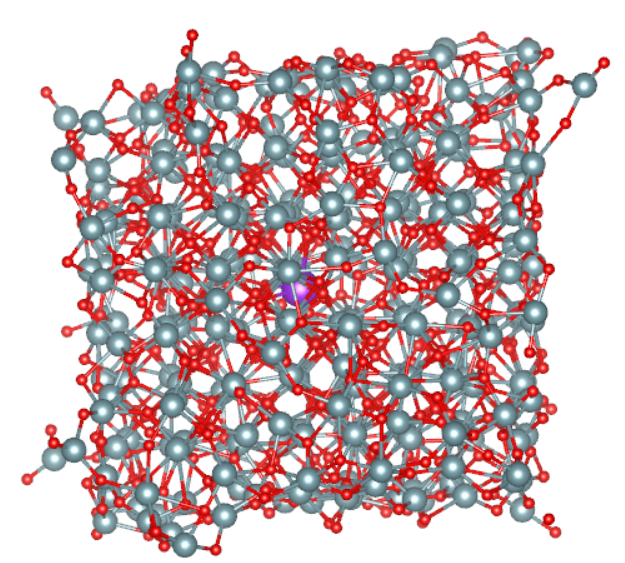
Рисунок 6 - Кристаллическая решетка диоксида урана в конечный момент времени моделирования:
большие шары – атомы урана; меньшие – атомы кислорода; фиолетовые – местоположение вакансии
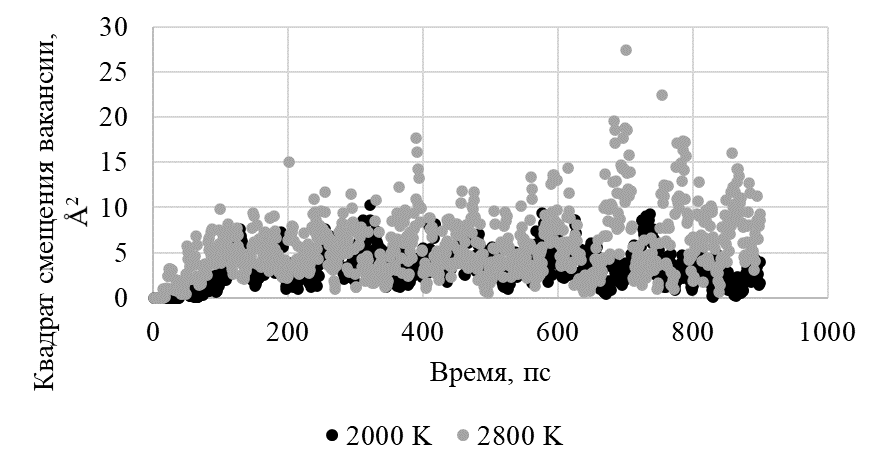
Рисунок 7 - Зависимость квадрата смещения вакансии от времени при температурах 2000 К и 2800 К
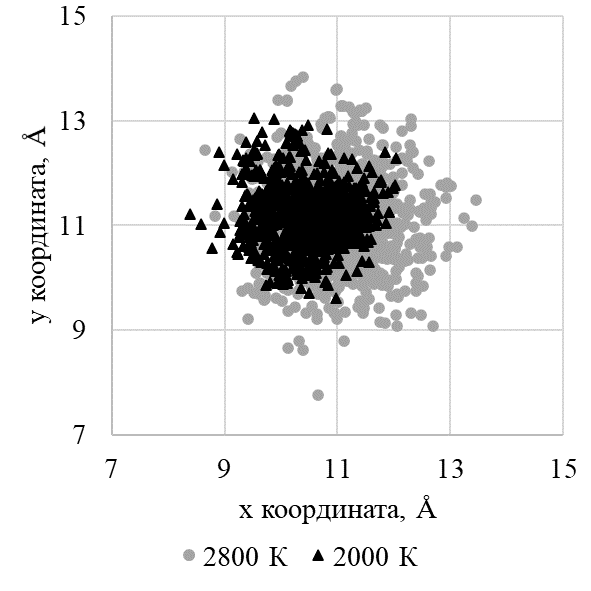
Рисунок 8 - Проекция координат катионной вакансии на плоскость xOy
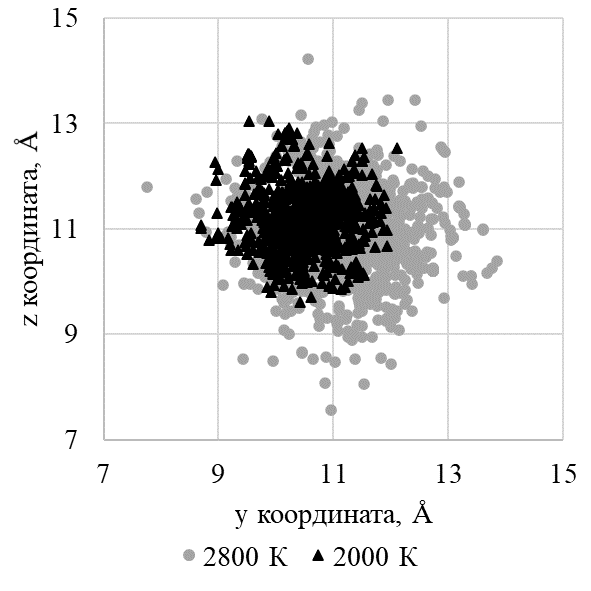
Рисунок 9 - Проекция координат катионной вакансии на плоскость zOx
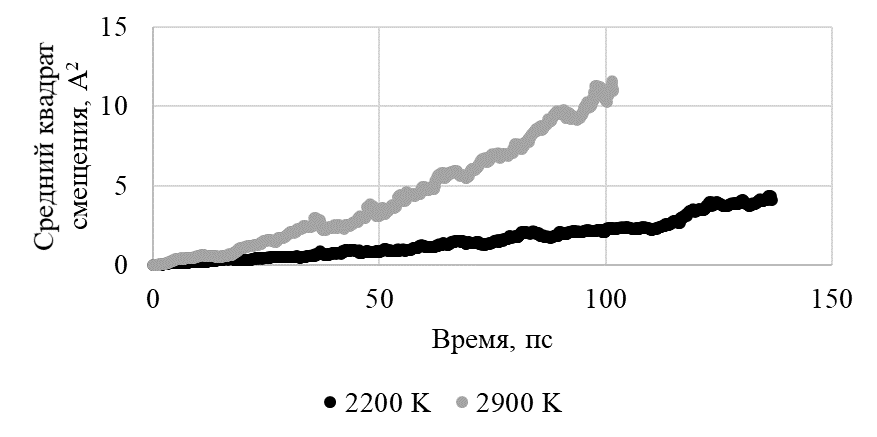
Рисунок 10 - Рост среднего квадрата смещения катионов со временем расчета
где 〈a2〉 – средний квадрат смещения, полученный из рисунка 11;
t – время процесса диффузии.
Температурная зависимость коэффициента диффузии имеет вид:
где E – энергия эффективной активации диффузии,
k – постоянная Больцмана, k=1,38∙10-23 Дж/K.
После преобразований формулы (10) можно получить зависимость логарифма коэффициента диффузии от обратной температуры. Угловой коэффициент полученной прямой будет равняться значению энергии эффективной активации диффузии.
Для построения необходимой зависимости были рассчитаны значения коэффициента диффузии для некоторых значений температур в диапазоне 2200-2900 К. В таблице 1 приведены рассчитанные значения коэффициента диффузии, обратной температуры, а также промежуточные величины. На рисунке 12 изображена вышеупомянутая зависимость.
Таблица 1 - Значения коэффициента диффузии катионов для соответствующих значений температуры кристалла
Температура кристалла, К | Коэффициент диффузии, см2/c ∙10-7 | Обратная температура 1/T, К-1∙10-4 | Логарифм коэффициента диффузии ln ln D |
2200 | 1,933 | 4,545 | -15,45 |
2300 | 1,686 | 4,348 | -15,59 |
2400 | 1,812 | 4,167 | -15,52 |
2500 | 3,393 | 4,000 | -14,89 |
2600 | 4,445 | 3,846 | -14,62 |
2700 | 4,637 | 3,704 | -14,58 |
2800 | 4,254 | 3,571 | -14,67 |
2900 | 7,131 | 3,448 | -14,15 |
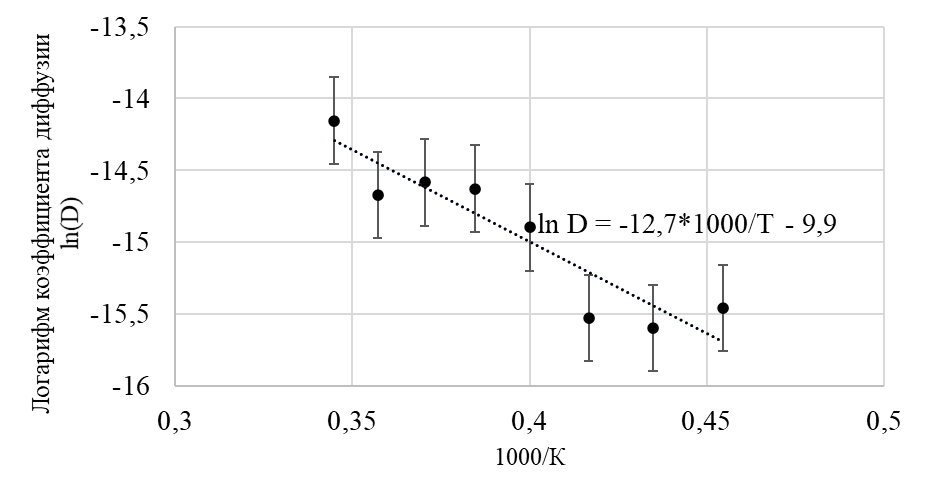
Рисунок 11 - Зависимость логарифма коэффициента диффузии от обратной температуры
Примечание: пунктирной линией изображена аппроксимирующая функция
Сравнивая уравнение (11) с аппроксимирующей функцией, приведенной на рисунке 12, делается вывод, что , тогда
.
Полученное значение энергии эффективной активации диффузии можно сравнить с экспериментальными и расчетными значениями для одиночной катионной вакансии – 1,5-3,0 эВ . Некоторое занижение значения, полученного в настоящей работе, может быть обусловлено присутствием анионных вакансий. Все три вакансии могут быть объединены в один вакансионный кластер, миграция которого осуществляется с большей инертностью.
7. Заключение
Таким образом, в работе предложена модель, описывающая поведение кристаллической структуры с точечным дефектом, построенная на методе молекулярной динамики. Модельными системами были кубические гранецентрированные кристаллиты размером в 765 частиц с точечным дефектом вакансионного типа. Граничные условия соблюдаются благодаря использованию термостата Берендсена, который поддерживает нужную температуру, отводя лишнюю энергию от решетки.
В качестве оценки миграции катионов построена зависимость логарифма коэффициента диффузии катионов от обратной температуры кристаллической решетки, предварительно были найдены сами значения коэффициента диффузии с помощью известной связи со средним квадратом смещения атомов в кристалле. Абсолютное значение углового коэффициента полученной с помощью линейной аппроксимации прямой дает значение эффективной энергии активации диффузии. Данная величина, равная 1,10 эВ, оказывается близкой к экспериментальным и расчетным значениям других авторов для одиночной катионной вакансии, находящимся в диапазоне 1,5-3,0 эВ. Несколько заниженный результат можно объяснить наличием помимо катионной вакансии двух анионных вакансий. Весь вакансионный кластер обладает меньшей подвижностью по сравнению с одиночной катионной вакансией.
