Modelling oscillations of a moving sheet with one rigid attachment condition
Modelling oscillations of a moving sheet with one rigid attachment condition
Abstract
This work is dedicated to the study and analysis of a model initial boundary value problem on propagation of vibrations in a moving elastic sheet with one condition of rigid attachment at the ends of the sheet. The main problem is to find exact solutions for this problem. To construct the desired solution, the projection method is used, in which a set of basis functions from the auxiliary boundary value problem for vibrations of an I-beam with hinged ends is used. The mathematical model of vibrations is a linear partial differential equation of the fourth order with constant coefficients, which contains a mixed derivative in time and spatial variable. A method of constructing explicit exact solutions of this problem is given, which can be generalized to similar sets of problems. The article contains illustrations showing the deviations of the web from the equilibrium position and the dynamics of oscillations at different moments of time.
1. Введение
Задача о колебаниях упругого полотна является одной из важных и интересных задач математики и механики. Такого рода задача возникает при производстве бумаги, проката жестяных листов и так далее. Решение такой задачи позволяет описать процесс колебаний упругого полотна, что может быть применено для задачи гашения возникающих колебаний, а именно задачи оптимального управления.
Основной сложностью, с которой приходится сталкиваться при решении данной проблемы, является невозможность применения стандартного метода разделения переменных для получения решения в виде ряда Фурье. Этот эффект обусловлен наличием слагаемого со смешанной производной.
Вопросы исследования колебаний, движущихся материалов и конструкций актуальны и важны в современном естествознании. За последнее время проведено множество исследований на эту тему.
В литературе уже представлены уравнения и частичные решения для подобного кластера задач. Данная работа предлагает метод поиска точных решений и подход к решению подобных задач.
В работах
, и авторы затрагивают основополагающие принципы в изучении динамики колебаний балок, в частности в работах и рассматривается уравнение, описывающее периодические колебания двутавровой балки.В работе
рассматриваются поперечные колебания нити с постоянной скоростью. Наиболее важная проблема, которую рассматривают авторы, связана с возникновением резонансных эффектов при поперечных колебаниях нити. Такие эффекты могут играть ключевую роль в механике различных структур, и их понимание имеет важное значение для разработки эффективных методов управления и предотвращения нежелательных деформаций.В работе
рассматривается неустойчивость аксиально движущейся упругой пластины. Авторы подробно анализируют этот процесс и выявляют факторы, приводящие к потере устойчивости. Это исследование имеет важное значение для понимания динамических характеристик и поведения упругих материалов в условиях аксиального движения. В работе авторы проводят статический анализ неустойчивости для подвижных мембран и пластин, взаимодействующих с идеальной жидкостью в аксиальном направлении.Для более глубокого понимания методов и техники вычислений, стоит обратить внимание на исследования, проведенные в
и . Эти работы содержат анализ типичных уравнений математической физики, создавая необходимый теоретический фундамент для понимания применяемых подходов.В
поднимаются вопросы, связанные с конкретными методами решения уравнений математической физики, что является существенным элементом для осмысленного анализа динамических процессов в структурах, таких как балка и полотно. Эти труды не только являются ключевыми для понимания математических концепций, применяемых в данном исследовании, но и представляют ценный источник для тех, кто стремится углубить свои знания в области математической физики и ее приложений в инженерии и науке.В работе
авторы представляют результаты, охватывающие численные методы для решения задач о колебании полотна, и подробно рассматривают аспекты гашения колебаний в контексте движущегося полотна.Работа
освещает методы анализа и подходы к управлению колебаниями струны с применением демпфирующих элементов.Рассмотренные вибрационные поведения движущихся балок Тимошенко в работе
при разного рода условиях закрепления на концах, являются хорошим подспорьем для изучения влияние краевых условий на вибрационное поведение движущейся двутавровой балки.В этой работе главным приемом для построения решений является проекционный метод, с помощью которого определяются коэффициенты при базисных функциях специальной порожденной системы алгебраических уравнений. Применение проекционного метода и более подробные аспекты использования приближений Галёркина можно найти в труде
, где автор детально исследовал этот метод, предоставив конкретные примеры решения задач.Основным уравнением работы является уравнение из работы колебаний движущегося упругого полотна:
Данное волновое уравнение определяет амплитуду поперечных колебаний движущегося полотна. Здесь
– функция, которая показывает на сколько от точки равновесия, отклоняется полотно в точке x в момент времени t,
v0 – скорость, с которой волна перемещается вдоль оси x,
c – скорость распространения колебаний в покоящемся полотне,
D – коэффициент жесткости на изгиб,
m – масса полотна на единицу площади.
2. Методы и принципы исследования
Из-за того, что в уравнении колебания движущегося упругого полотна появляется слагаемое со смешанной производной, явно не удается применить метод разделения переменных. Поэтому для поиска точных решений, будет применяться модификация метода разделения переменных. Этот метод заключается в определении вида решения исходной задачи. Для этого этапа необходимым является отыскания функционального базиса решений вспомогательной краевой задачи, в данной статье эта роль отводится начально краевой задачи для двутавровой балки, для которой метод разделения переменных применим.
2.1. Поиск решения уравнения
Рассмотрим задачу о колебаниях двутавровой балки:
где при помощи уравнения (1) можем вывести следующие соотношения: и
, а также необходимо наложить ограничение:
, следовательно, и
, откуда несложно получить наложенное на уравнение следующее ограничение:
Краевые условия для уравнения (2):
а в качестве начальных условий имеем:
Применим известный метод Фурье разделения переменных для задачи (2), (4), (5). И получим следующее уравнение для поиска собственных функций и чисел:
Откуда получается такое характеристическое уравнение:
В таком случае корнями характеристического уравнения являются: , где в свою очереди для краткости и удобства была введена переменная
, под корнем можно рассматривать два случая, когда
и когда
, а в таком случае получается мнимая единица и, следовательно,
можно записать в таком виде:
будем рассматривать только случай, когда под корнем в
отрицательное выражение, то есть данные корни комплексные. Параметр
будет определен позже. Для получения комплексных корней в ходе решения было наложено следующее ограничение:
откуда используя введенные: получаем:
Собственные функции имеют следующий вид:
Для того чтобы найти неизвестные C, D, A и B в формуле (7), необходимо воспользоваться краевыми условиями (4), а именно, , используя данные условия можно получить следующую систему уравнений:
Известно, что однородная система (8) имеет нетривиальное решение относительно неизвестных коэффициентов C, D, A и B тогда и только тогда, когда ее определить будет равен нулю, а тогда получаем:
Для получения собственных значений задачи (2), (4)–(5), из уравнения (9) выводится трансцендентное уравнение:
разделив это уравнение на , несложно получить:
где Уравнение (10) является трансцендентным уравнением, для которого нет явной формулы для определения его корней. Искать корни можно численными методами, а здесь мы получим асимптотическое поведение искомых корней.
Следуя трудам и введем функцию , которая возрастает на
и убывающую при
. Функция
также убывает при
как суперпозиция возрастающей и убывающей функций. Так как
и , то на интервале
нет корней уравнения (10), а на каждом интервале
, существует единственный корень qn уравнения (10). Подставим qn в уравнение (10) и получим:
следуя работе получаем, что , таким образом,
, используя
и формулу (11) имеем:
Функция убывает на
и принимает значения
Таким образом, согласно (10) и всем введенным обозначениям собственные значения задачи (2), (4)–(5) могут быть представлены следующей формулой:
А собственные функции при этом будут иметь следующий вид:
где .
Далее, получаем функцию u(x,t):
,
где берется из формулы (12), а
можно получить стандартным методом.
Итак, теперь, когда вспомогательная задача была решена, можно перейти к отысканию точных решений основной задачи. Для этого необходимо использовать полученные собственные функции (12) вспомогательной задачи (2), (4)–(5). Имеем основное уравнение, описывающее колебания упругого движущегося полотна (1), в качестве граничных условий закрепления возьмем условия (4).
Решение уравнения (1) будем искать в виде берутся со вспомогательной задачи. Далее подставляем
в изначальное уравнение (1) и получаем:
После сокращения на получаем дифференциальное уравнение второго порядка с постоянными коэффициентами, искомая функция которого зависит лишь от переменной t. Для этого уравнения, будем рассматривать случай несовпадающих корней характеристического уравнения, то есть нерезонансный случай. После применения стандартных методов, выписываем решение этого уравнения с неизвестными коэффициентами:
Теперь можем записать решение для функции в виде конечной суммы:
Далее для того, чтобы определить а также поиска точных решений будем рассматривать начально-краевую задачу для уравнения (1) с краевыми условиями (4).
Пример. Рассмотрим следующую начально-краевую задачу:
Пусть непосредственной проверкой легко убедиться в выполнении краевых условий (4), то есть выполнено согласование начальных данных с краевыми условиями, что не противоречит существованию решения.
Для определения точного решения данной задачи необходимо разложить в ряд Фурье функцию f(x) по синусам, чтобы в дальнейшем представить получившиеся в ходе разложения синусы как комбинацию из экспонент и определить искомые коэффициенты разложения. Раскладывая данную функцию, получаем следующее соотношение:
При нахождении точного решения поставленной задачи необходимо воспользоваться формулой Эйлера для синуса: и применить данную формулу к нашей функции f(x), получившееся соотношение позволяет использовать формулу (15) с
. В дальнейшем для упрощения вычислении введем следующий вспомогательный параметр
. Неизвестные коэффициенты можно определить благодаря начальным условиям (16).
После этого, окончательное точное решение записывается в следующем виде:
Далее, продемонстрируем полученное решение (17) на графике, иллюстрации можно увидеть ниже, на них смоделировано полученное решение на координатной плоскости и заданы следующие параметры: . И в моменты времени t = 0,1 и 1,9. Можно наблюдать моделирование динамики изменений колебаний решения (17), решенной задачи (см. рис. 1–3).
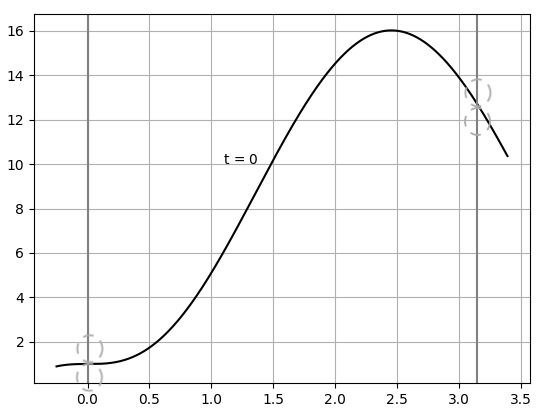
Рисунок 1 - График решения (17) в момент времени t = 0
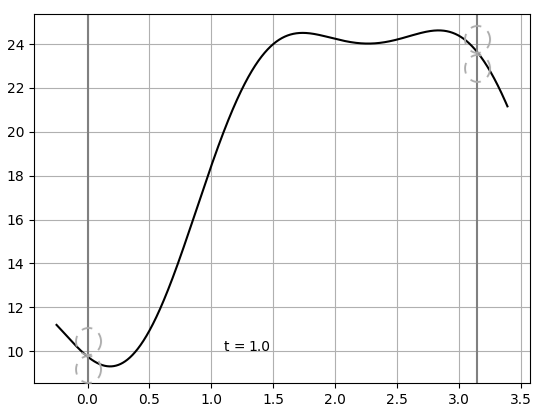
Рисунок 2 - График решения (17) в момент времени t = 1
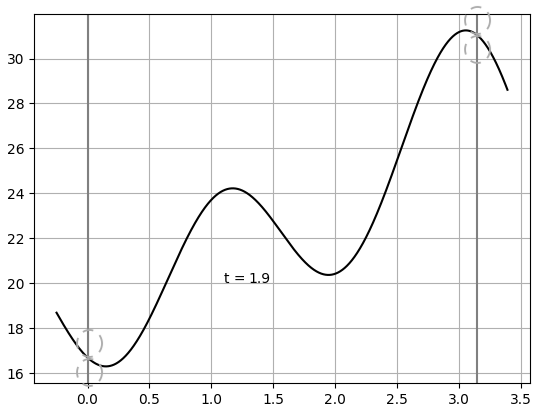
Рисунок 3 - График решения (17) в момент времени t = 1.9
Изменяя параметры, которые присутствуют в решении можно убедиться в крепкой зависимости поведения колебаний от изменения данных параметров. Например, можно изучить и оценить то, как изменение жесткости или массы полотна влияет на его колебания.
3. Основные результаты и обсуждение
Проведенные исследования свидетельствуют о разнообразии волновых режимов в движущемся упругом полотне.
Экспериментальные изменения параметров, таких как скорость, жесткость и вес полотна, существенно влияют на динамику колебаний.
Уменьшение веса приводит к увеличению скорости распространения волн и частоты колебаний. Увеличение скорости сопровождается уменьшением длины волны и увеличением частоты колебаний.
Построение решения в виде рядов позволяют описывать и предсказывать поведение колебательного процесса. При этом нет необходимости применять методы вычислительной математики, так как получены явные решения.
Результаты исследования представляют огромный интерес не только с практической, но и с теоретической точки зрения. С одной стороны, они расширяют знания о физических процессах в движущемся упругом полотне с шарнирно опертыми условиями закрепления. С другой стороны, эти результаты могут стать основой для разработки новых материалов и технологий, где упругие волны играют важную роль.
Вследствие проведенных исследований можно сказать, что колебания движущегося упругого полотна представляют собой сложное явление, зависящее от многих факторов. Однако благодаря новому методу удалось успешно описать эти колебания, что открывает перспективы для более глубокого понимания и использования этих процессов.
4. Заключение
В работе рассмотрены колебания движущегося упругого полотна, а в качестве математической модели, которое бы описывало данный процесс была рассмотрена начально-краевая задача для уравнения 4-го порядка со смешанной производной с постоянными коэффициентами жесткости, массы, скорости волны и скорости распространения колебаний в покоящемся полотне.
Для представленных задач с выдвинутыми шарнирно опертыми условиями закрепления и поставленными начальными условиями, специального вида, получены семейства точных решений. Приведено решение для начальной функции, в частности решение представленной в виде полинома 6-ой степени.
Также была выполнена визуализация решения соответствующей начально-краевой задачи в разные моменты времени на рисунках.
