Solving logistics problems with the Stamm 4.3 application

Использование компьютерного моделирования при решении задач оптимизации логистики предполагает некоторые особенности

1. Автоматизация процесса принятия решений. Компьютерное моделирование позволяет быстро создавать и анализировать различные сценарии, что упрощает процесс принятия решений.

2. Учет большого количества факторов. Логистические системы могут быть очень сложными и включать множество факторов, таких как время доставки, стоимость перевозки, объем груза и т.д. Компьютерное моделирование позволяет учитывать все эти факторы и оптимизировать работу системы в целом.

3. Возможность проведения экспериментов. С помощью компьютерного моделирования можно проводить эксперименты и проверять различные гипотезы, что позволяет улучшить работу логистической системы.

4. Более точный анализ данных. Компьютерное моделирование позволяет проводить более точный анализ данных и выявлять скрытые закономерности, что может привести к более эффективной оптимизации логистической системы.

5. Снижение рисков. Компьютерное моделирование позволяет предсказать возможные проблемы и риски, связанные с логистической системой, что позволяет принимать меры для их минимизации.

Существует значительное количество программного обеспечения, которое может использоваться для решения логистических задач. Отметим среди наиболее известных, выделяя особенности:

1. Excel – один из самых популярных инструментов для подобной цели. Он позволяет создавать таблицы, графики и диаграммы, а также проводить анализ данных и оптимизацию.

2. MATLAB – мощный инструмент для решения математических задач, включая логистические. Он предоставляет широкий спектр функций и инструментов для анализа данных, моделирования и оптимизации.

3. GAMS (General Algebraic Modeling System) – программное обеспечение, которое используется для моделирования и оптимизации логистических систем. Оно позволяет создавать и решать сложные математические модели с помощью специального языка моделирования.

4. Llamasoft – программное обеспечение, которое используется для оптимизации логистических систем и управления цепями поставок. Оно позволяет проводить анализ данных, моделирование и оптимизацию, а также предоставляет инструменты для управления рисками и принятия решений.

5. Simul8 – программное обеспечение, которое используется для моделирования и оптимизации бизнес-процессов и логистических систем. Оно позволяет создавать имитационные модели, анализировать данные и проводить оптимизацию.

6. AnyLogic – среда имитационного моделирования, используемая для моделирования и оптимизации сложных систем, включая логистические. Она предоставляет широкий спектр инструментов для моделирования, анализа и оптимизации, а также позволяет использовать различные методы моделирования, включая системную динамику, агентное моделирование и дискретно-событийное моделирование.

Кроме того, имеется много программных продуктов, решающих строго ограниченный перечень задач, например, использование динамического и стохастического программирования для решения оптимизационных задач

По данным компании XJ Technologies (производителя упомянутого выше пакета Anylogic), наибольшим спросом сегодня пользуются именно имитационные модели, реализованные для области логистики

Рассмотренные выше пакеты программ в той или иной степени решают обозначенные проблемы при компьютерном моделировании логистических задач, обладая при этом определенными недостатками. Например, все вышеперечисленное – это коммерческие продукты с приличной ценой, кроме того, в связи с политикой западных санкций в отношении России многие из них просто недоступны нашим потребителям

В качестве объекта исследования в данной работе выступают типовые логистические задачи. Для их решения используется некоммерческий продукт Stamm 4.3.

Данное приложение разрабатывается и совершенствуется автором более 20 лет, и если изначально система предназначалась для организации простейшего имитационного моделирования с помощью электронных таблиц, то в настоящее время доступны ряд функций, которые позволяют решать самые разные задачи

В качестве примера рассмотрим простейшую задачу оптимизации запасов, реализованную с помощью Excel. Данная модель учитывает однопериодную модель управления запасами. Необходимо определить размер заказываемой партии Part на какой-то будущий промежуток времени, если известно, что спрос D – случайная величина с нормальным законом распределения (среднее значение равно Mс, среднее квадратическое отклонение – Sс). В том случае, если спрос будет меньше той партии, которая была заказана, то издержки составят величину

где Ch – стоимость хранения единицы товара.

В случае, если заказанной партии окажется недостаточно для удовлетворения спроса, то затраты будут включать издержки дефицита

где Cd – штраф за дефицит единицы товара.

Задача решается многократным проигрыванием ситуации на складе с учетом заданного закона распределения спроса. В случае использования Excel имеет место псевдо-имитационное моделирование, так как варьирование спроса осуществляется в результате изменения связанных ячеек в соседних строках, а такие параметры модели как начальный уровень запаса и объем производства вводятся в модель вручную (рис. 1). Это связано с ограничениями Excel на использование перекрестных ссылок.

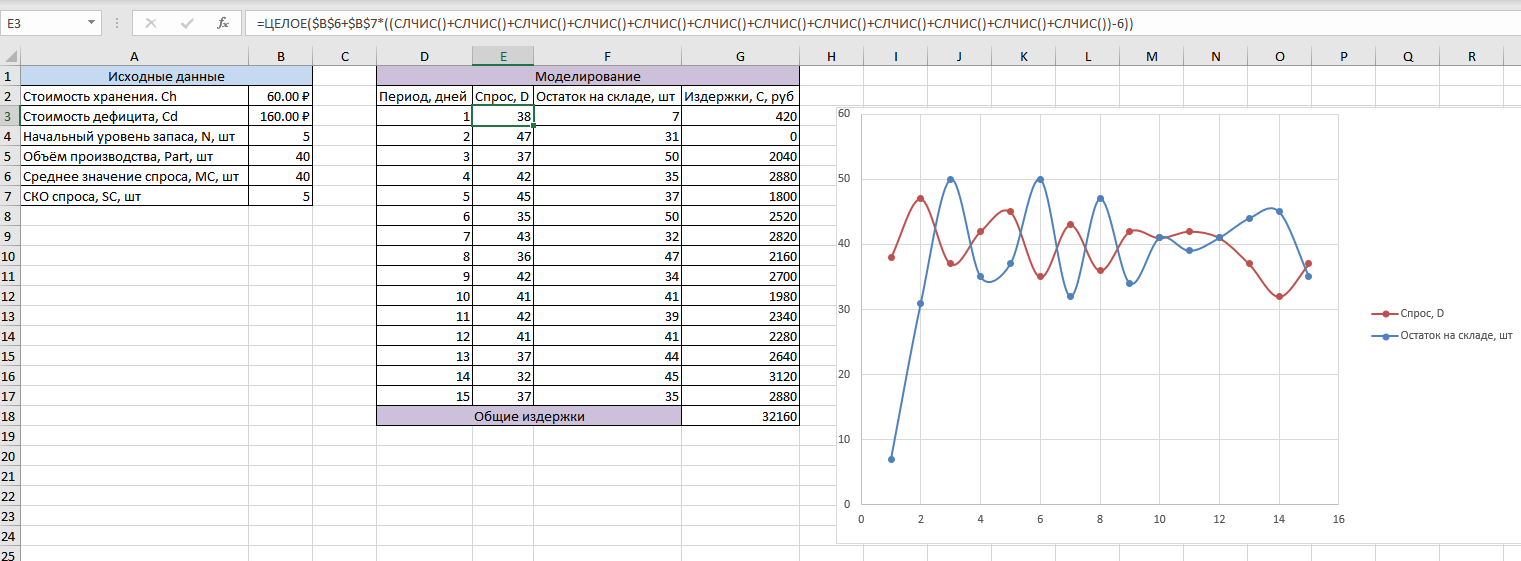
Рисунок 1 - Моделирование системы с однопериодным пополнением запаса в Excel

DOI:10.60797/IRJ.2024.143.145.1

В случае потребности в многошаговом Монте-Карло использовать такую модель не очень удобно. Эта же задача в Stamm решается намного проще и выглядит компактнее (рис. 2).

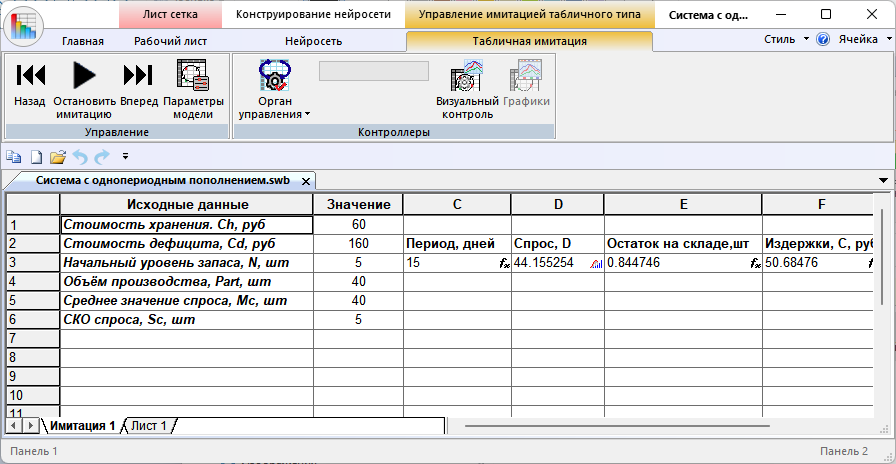
Рисунок 2 - Моделирование системы с однопериодным пополнением запаса в Stamm 4.3

DOI:10.60797/IRJ.2024.143.145.2

При этом наблюдать за изменением системы можно в отдельном окне, добавляя туда необходимые для контроля переменные (рис. 3).

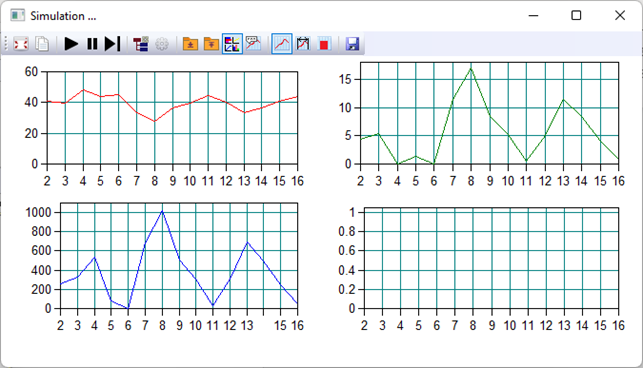
Рисунок 3 - Окно контроля параметров при табличной имитации

Примечание: Stamm 4.3

DOI:10.60797/IRJ.2024.143.145.3

Однако наиболее удобно решать оптимизационные задачи логистики, используя весь потенциал рассматриваемой системы. Имеется ряд разноплановых задач оптимизации логистических систем, тем не менее имеющих схожие элементы.

Укрупненный алгоритм имитации с помощью ячеек в таблице предусматривает следующие действия (рис. 4). Инициализацию переменных виртуального модельного времени – начального значения (T0), конечного (Tmax) и шага моделирования (ΔT).

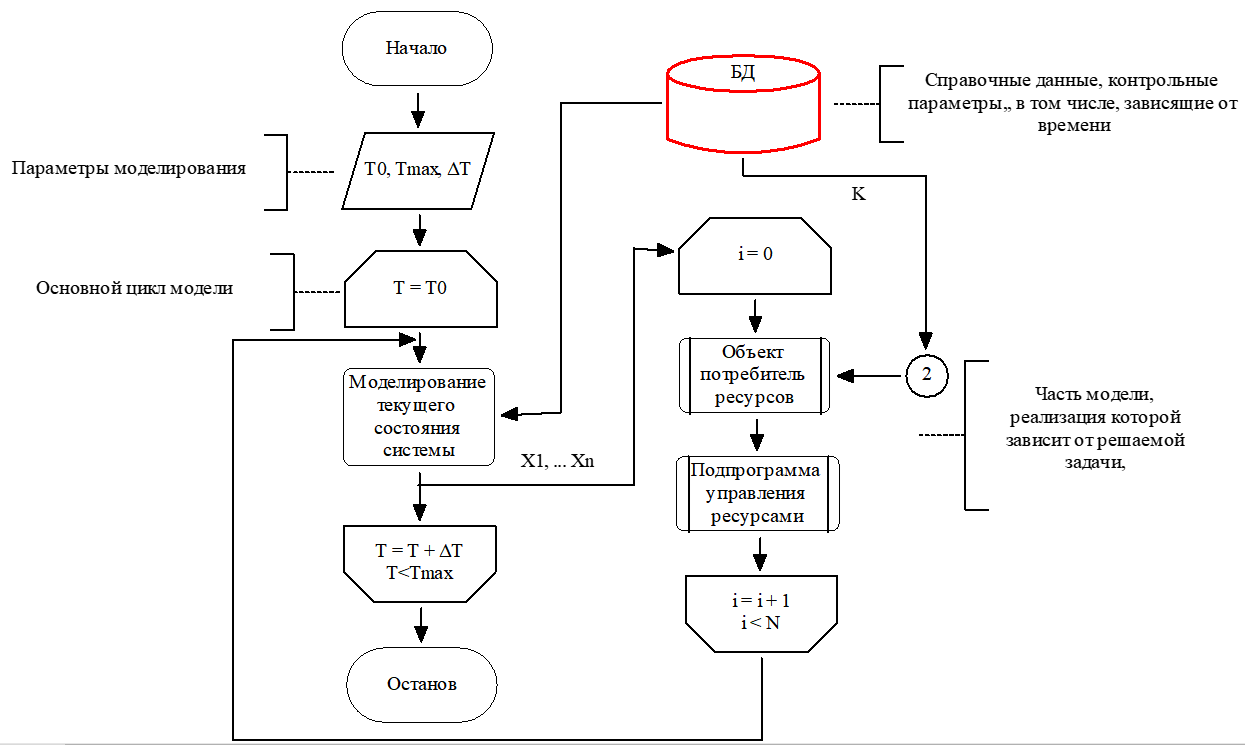
Рисунок 4 - Основной алгоритм табличной имитации

Примечание: Stamm 4.3

DOI:10.60797/IRJ.2024.143.145.4

До истечения модельного времени выполняется цикл, на каждом шаге которого определяется текущее состояние системы, в том числе внутри главного цикла модели при необходимости имеется вложенный цикл, обрабатывающий состояние конечного числа однотипных виртуальных объектов. Такие объекты в соответствии с принципами объектно-ориентированного моделирования имеют одинаковые структуру, набор переменных параметров, связи с другими компонентами модели.

В случае решения большого круга задач в области логистики на транспорте, можно выделить объекты класса «Потребитель ресурсов». Экземплярами такого класса могут быть, например, автомобили, расходующие в процессе эксплуатации топливо, шины и т.п. Этот расход Y является функций внешних и иных факторов (X1, X2, … Xn) и времени. В свою очередь, этот класс имеет два принципиально разных производных класса, непрерывно расходующих ресурс с течением времени и потребляющие его дискретно. К особенностям последнего можно отнести изменение своего состояния в процессе потребления ресурса. Примерами второго подкласса являются автомобили, периодически проходящие плановое техническое обслуживание и нуждающиеся в замене некоторых деталей, масла и т.п. На рисунке 5 представлен алгоритм обработки объектов такого класса в табличной имитации. Данный алгоритм, как и сам класс, является абстрактным, его конкретная реализация будет зависеть от особенностей моделируемого объекта.

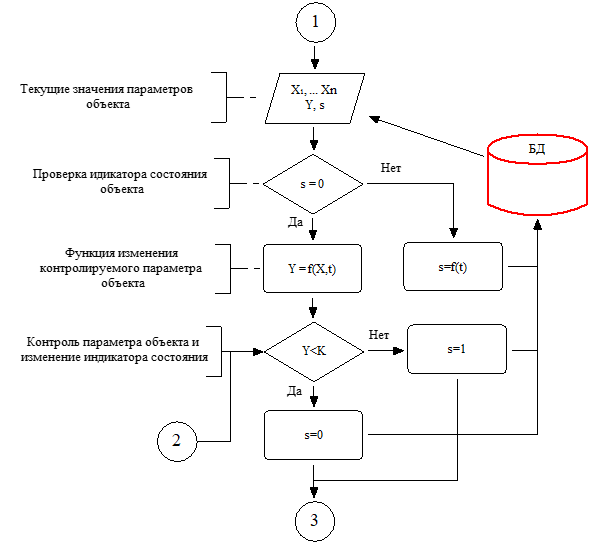
Рисунок 5 - Шаблон алгоритма «Объект потребитель ресурсов» в программе Stamm 4.3

DOI:10.60797/IRJ.2024.143.145.5

В процессе имитационного моделирования логистических задач, предусматривающих в качестве компонентов модели большого числа однотипных объектов, таких как автомобили, с целью экономии памяти ПК нецелесообразно использовать копии каждого из них во время всей жизни модели. Рассматриваемая в работе имитационная модель на базе электронных таблиц предусматривает обработку всех объектов на каждом шаге моделирования с чтением текущего состояния из базы данных и дальнейшим сохранением изменений (рис. 4, 5).

С использованием рассмотренных подходов было разработано несколько имитационных моделей в системе Stamm. Например, модель оптимизации запасов пневмобалонов автобусов (рис. 6).

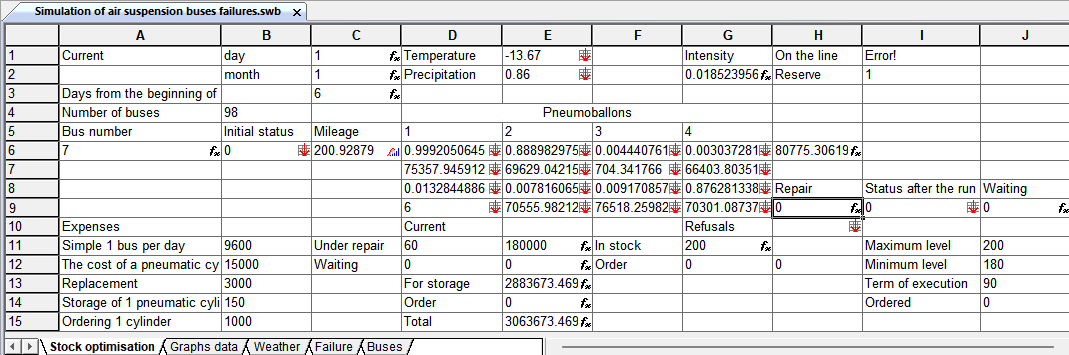
Рисунок 6 - Модель оптимизации запасов пневмобаллонов в программе Stamm 4.3

DOI:10.60797/IRJ.2024.143.145.6

Воспроизведение состояния пневмоподвески автобусов осуществляется в ячейках A6..J9. Данные о текущем состоянии по автобусу моделируются с помощью специальных ячеек-контроллеров (рис. 7).

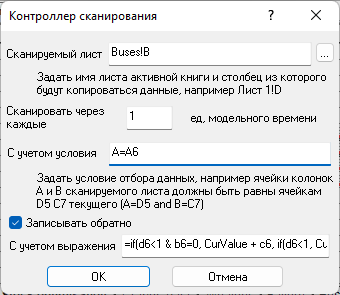
Рисунок 7 - Ячейка-контроллер для обмена данными с таблицей «Buses»

DOI:10.60797/IRJ.2024.143.145.7

Содержимое таблицы «Buses» изменяется по каждому автобусу при изменении модельного времени (рис. 8). Факторы, влияющие на расход ресурса пневмобалонов, содержатся в ячейках E1, E2, G2 таблицы, содержащей имитационную модель «Stock optimisation» (рис. 6), они, в свою очередь, зависят от температуры окружающей среды и других условий эксплуатации, представленных в табличном виде, лист «Weather» (рис. 9).

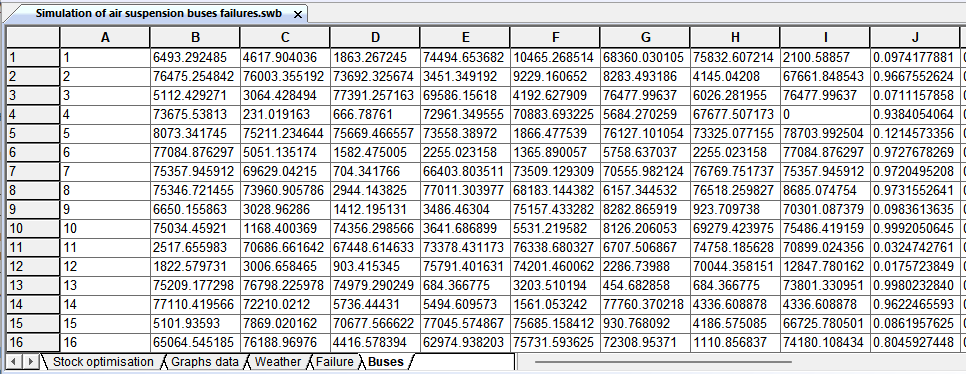
Рисунок 8 - Лист с актуальными данными о состоянии автобусов «Buses»

DOI:10.60797/IRJ.2024.143.145.8

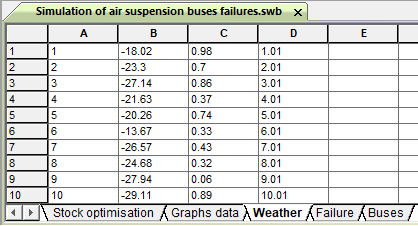
Рисунок 9 - Лист с прогнозными данными о погоде и интенсивности эксплуатации «Weather»

DOI:10.60797/IRJ.2024.143.145.9

С использованием аналогичных алгоритмов разработаны также модели управления логистикой при ремонте и обслуживании вертолетного парка «Ютейр» на Севере Тюменской области (рис. 10) и ряд других.

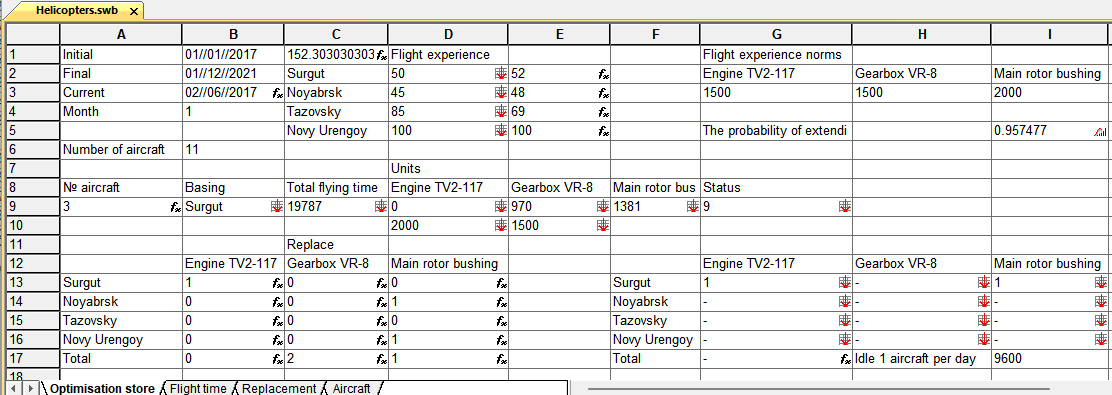
Рисунок 10 - Табличная имитационная модель «Управление логистикой основных агрегатов к местам базирования вертолетов»

DOI:10.60797/IRJ.2024.143.145.10

Предложенные методы организации имитационных моделей табличного типа позволят сократить время на их разработку, а также использовать базу данных текущего состояния объектов в ходе имитационного эксперимента для дополнительного анализа и принятия решений как в ходе моделирования, так и при его завершении. Полученные результаты легко могут быть перенесены из рабочих листов Stamm в другие приложения, например, Excel.