ALGORITHMS TO DETERMINE SOLVABILITY OF LINEAR INTEGRO-DIFFERENTIAL EQUATIONS WITH ANALYTIC FUNCTIONS
АЛГОРИТМЫ ОПРЕДЕЛЕНИЯ РАЗРЕШИМОСТИ ЛИНЕЙНЫХ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С АНАЛИТИЧЕСКИМИ ФУНКЦИЯМИ
Научная статья
Мураталиева В.Т. *
ORCID: 0000-0002-7246-7529,
Международный университет Кыргызстана, Бишкек, Киргизия
* Корреспондирующий автор (vmuratalieva70[at]mail.ru)
АннотацияПрименение метода степенных рядов к линейным интегро-дифференциальным уравнениям приводит к бесконечным системам линейных алгебраических уравнений для коэффициентов этих рядов. Если уравнение содержит несколько членов, то практически невозможно построить такую систему и сделать определенный вывод. Поскольку некоторые исходные уравнения таких систем отличаются от других, мы предложили использовать компьютер для их подходящего представления. Кроме того, мы нашли достаточные условия на линейные интегро-дифференциальные уравнения Вольтерра третьего рода, являющиеся правильными в аналитических функциях, которые обобщают известный факт корректности интегрального уравнения Вольтерра второго рода.
Ключевые слова: интегральное уравнение, линейное уравнение, уравнение типа Вольтерра, алгоритм, аналитическая функция.
ALGORITHMS TO DETERMINE SOLVABILITY OF LINEAR INTEGRO-DIFFERENTIAL EQUATIONS WITH ANALYTIC FUNCTIONS
Research article
Muratalieva V.T. *
ORCID: 0000-0002-7246-7529,
International University of the Kyrgyz Republic, Bishkek, Kyrgyz Republic
* Corresponding author (vmuratalieva70[at]mail.ru)
AbstractApplying the method of power series to linear integro-differential equations yields vast infinite systems of linear algebraic equations for coefficients of these series. If the equation contains some members then it is practically impossible to construct such system and make a definite conclusion. As some initial equations of such systems differ from others, we proposed to use computer for their suitable presentation. Further, we found sufficient conditions on linear Volterra integro-differential equations of the third kind to be correct in analytical functions which generalize the well-known fact of correctness of a Volterra integral equation of the second kind.
Keywords: integral equation, linear equation, Volterra equation, algorithm, analytical functions.
- Introduction
Investigation of Volterra integro-differential equations was initiated in [1]. We will consider linear ordinary equations in this paper. As is customary, if the equation can be rewritten as u(m)(t) =Y(u(s),0 ≤ s ≤ t) where the right hand part depends (continuously) on past only and contains lower derivatives and integrals then it is said to be a Volterra equation of the second kind; one of type p(t)u(m)(t) = Y(u(s),0 ≤ s ≤ t) (the function p(t) sometimes vanishes but is not zero) is said to be a Volterra equation of the third kind.
Taylor series (power series) method for linear equations with analytical functions was proposed in [3] and [4]. Applying this method yields infinite systems of linear algebraic equations for coefficients of these series.
The paper [3] deals with equations of the second kind.
The paper [4] contains an algorithm to construct Taylor series segments for solutions of equations of the third kind.
In this paper we distinguish such class of linear Volterra integro-differential equations of the third kind with kernels being polynomials that their solvability in analytical functions is resolved algorithmically. Some particular cases of such algorithm were published in [2], [5], [6].
Remark 1. We do not mention numerous works on numerical (approximate) solving of initial value problems for Volterra equations; we consider ”exact” solving only.
Section 2 contains algorithm of solvability of auxiliary infinite system of linear algebraic equations. The main condition is that the matrix of coefficients is finite diagonal.
Section 3 describes differential and Volterra integral operators involved into equations, their properties and reducing some linear Volterra integro-differential equations of the third kind to ones in Section 2. This yield a corresponding algorithm of solvability of these equations.
Section 4 contains examples both an illustration of the theorem of Section 3 and relevance of its conditions.
We will use denotations
| R := (-∞;∞); R+ := [0; ∞); R++ := (0; ∞); Z := {..., -2, -1, 0, 1, 2, 3, ...}; N0 := {0, 1, 2, 3, ...}; N := { 1, 2, 3, ...}. |
We will use the term ”Algorithm” as it is usually understood in Analysis: arithmetical operations and comparison over numbers in R (for rational numbers this definition coincides with the strict one).
We will write discrete arguments in brackets to bring denotations nearer to algorithmic ones and to bypass the common ambiguity of expressions such as a2j.
- Algorithmically resolvable infinite linear algebraic systems
We will consider the space Ωθ , θ < R++ , θ < 1 of sequences { f [n]| n ϵ N0} fulfilling the condition ( ∃ γ ϵ R++ )( ∀n ϵ N0 )( | f [n]| ϵ γ θn ).
Consider the infinite system of linear algebraic equations ( µ,ν ϵ N0 )
(1) Theorem 1. If f ϵ Ω θ and (2) then there exists an algorithm of resolving the system (1) in Ω θ .Proof. Denote α :=| a[J + 1, J + 1 + µ] |, then ( ∀j > J)( |a[ j, j + µ]| ≥ α ). Consider the finite system of linear algebraic equations
(3) The algorithm to solve such systems (unique solution; no solutions; infinitely many solutions) is well-known.If it has no solutions then the equation (1) has no solutions too. Otherwise, let {u0[k] | k ϵ 0..J + µ} fulfil (3).
Denote γ1 such that ( ∀k ϵ 0..Ј+μ )( |u[k]|≤ γ1 θk ); γ2:=max{ γ1, γ2 /α/(1-β)}.
Rewrite the system (1) in the form
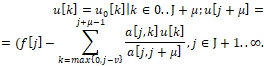 (4)
(4)
All u[ j] are defined.
We are to prove that (∀k ϵ N0)(|u[k]| ≤ γ2θk). By induction, for j > J:
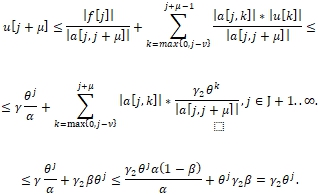
- Algorithm for linear integro-differential equations
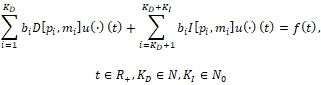 (5)
(if KI = 0 then integral terms are absent)
f (t) ϵ Λr; 0 ≠ bi ϵ R; all pairs (pi, mi) are different.
(5)
(if KI = 0 then integral terms are absent)
f (t) ϵ Λr; 0 ≠ bi ϵ R; all pairs (pi, mi) are different.
Introduce the function ”rung”
![]()
![]()
We will use the rule ”zero · indefinite = zero”. We have for power functions
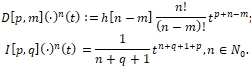 (6)
(6)
Substituting (6) into (5) and equating coefficients by powers of t we obtain that the differential term makes the contribution bL[k - p, m]u[k - p + m] to the equation with f [k], k ϵ N0 where
![]()
The integral term does the following one bQ[k - p, q]u[k - p - 1 - q] where
![]()
Thus, we obtain the infinite system of linear algebraic equations
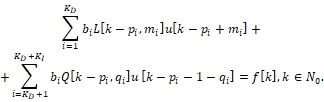 (7)
Denote
(7)
Denote
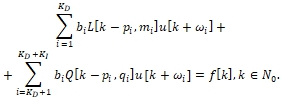 (8)
Denote WD := max{ωi | i = 1..KD}; WI := max{ωi | i = KD + 1..KD + KI};
PD := max{pi | i = 1..KD; ωi = WD} in (8).
(8)
Denote WD := max{ωi | i = 1..KD}; WI := max{ωi | i = KD + 1..KD + KI};
PD := max{pi | i = 1..KD; ωi = WD} in (8).
Re-denoting and rearranging the system (8) we obtain a system of type (1).
Theorem 2. If A1) WD ≥ 0; A2) either integral terms absent or
![]() (9)
(9)
A3) (ωi < WD) ⇒ (pi ≤ PD) then there exists an algorithm to solve the equation (5) in Ωr.
Proof. Consider the corresponding system of linear algebraic equations (8). For large k we obtain:
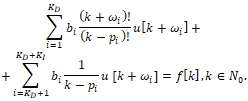 (10)
(10)
Consider the coefficients by u[k + WD]. There are ![]() , possibly
, possibly ![]() for some p'<PD and possibly
for some p'<PD and possibly ![]() for some p''. Without loss of generality, let bi = 1 by G[k]. We have
for some p''. Without loss of generality, let bi = 1 by G[k]. We have
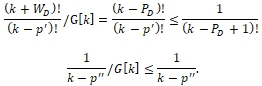
Also, for terms with ωi < WD, in the first sum (by the condition of Theorem)
![]()
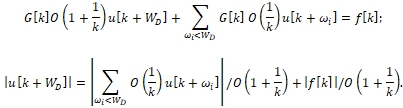
For sufficiently large k the condition (2) fulfils.
Remark 3. To apply Theorem 2 it is sufficient to find such J'ϵ N that the leading term with u[ j + WD] is not zero since j > J'.
- Examples of linear integro-differential equations
Example 1 (an illustration to Theorem 2). Consider the following equation
![]() (11)
(11)
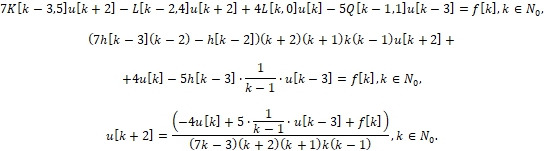 Some initial equations:
Some initial equations:
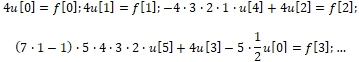 Solution:
Solution:
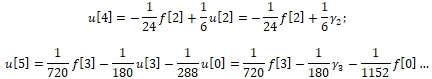 The simplest
The simplest
Example 2 (sufficiency of condition A1). The following equation tu(t) = 1
(WD = ω1 = m1 - p1 = 0 - 1 = -1) does not have an analytical solution.
Example 3 (sufficiency of condition A2). Consider the following equation
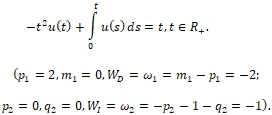 (12)
The formal series u(t) = 1 + 2t + 2*3t2 + ... + (n + 1)!tn + ... exists but does not converge.
Example 4 (sufficiency of condition A3). Consider the following equation
(12)
The formal series u(t) = 1 + 2t + 2*3t2 + ... + (n + 1)!tn + ... exists but does not converge.
Example 4 (sufficiency of condition A3). Consider the following equation
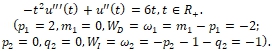 (13)
The formal series
u(t) = u[3]t3 + u[4]t4 + u[5]t5 + ... + u[n]tn + ...,
u[3] = 1, u[k + 1] = u[k] (k-1)(k-2)/(k+1), k = 3..∞
(13)
The formal series
u(t) = u[3]t3 + u[4]t4 + u[5]t5 + ... + u[n]tn + ...,
u[3] = 1, u[k + 1] = u[k] (k-1)(k-2)/(k+1), k = 3..∞
exists but does not converge.
Example 5 (a well-known result as a consequence of Theorem 2). Consider the linear Volterra integro-differential equation of the second kind
![]() (14)
(14)
Here WD = KD > 0, WI < 0 and there exists an analytical solution.
- Conclusion
The paper demonstrates the following. The technique to split the problem into a ”finite but complicated” part and an ”infinite but regular” one can yield resolving algorithms for sufficiently general types of equations with analytical functions.
| Конфликт интересов Не указан | Conflict of Interest None declarated |
Список литературы / References
- Volterra V. Lecons sur les equations integrales et les equations integro-differentielles / V. Volterra – Paris: Gauthier-Villars, 1913.
- Мураталиева В.Т. Спектральные свойства линейных уравнений с аналитическими функциями / В.Т. Мураталиева - LAP Lambert Academic Publishing. - Saarbrucken, 2017. - 57 с.
- Jaradat H.M. Series solution to the high-order integro-differential equations / H. M.Jaradat, F.Awawdeh, O. Alsayyed // Analele Universitatii, Oradea Fasc. Matematica.- 2009.- Tom XVI.- P. 247-257.
- Rashidinia J. Taylor series method for the system of linear Volterra integro-differential equations / J.Rashidinia, A. Tahmasebi // Journal of Mathematics and Computer Science.- 2012.- Vol. 4 No. 3.- P. 331-343.
- Мураталиева В.Т. Method and algorithm to investigate integro-differential equations with analytical functions / В.Т. Мураталиева // Тезисы III Международной научн. конф. ”Борубаевские чтения” 2019 г., Бишкек / Институт Математики Национальной академии наук Кыргызской республики.- Бишкек, 2019.- С. 48.
- Мураталиева В.Т. Алгоритм для исследования спектральных свойств линейных задач с аналитическими функциями / В.Т. Мураталиева // Вестник Жалал-Абадского гос.университета. – 2016.- №1(32).- C. 55–59.
Список литературы на английском языке / References in English
- Volterra V. Lecons sur les equations integrales et les equations integro-differentielles / V. Volterra – Paris: Gauthier-Villars, 1913.
- Muratalieva V.T. Spektral'nye svojstva linejnyh uravnenij s analiticheskimi funkcijami [Spectral properties of linear equations with analytic functions] / V.T. Muratalieva - LAP Lambert Academic Publishing. - Saarbrucken, 2017.-57 p. [in Russian]
- Jaradat H.M. Series solution to the high-order integro-differential equations / H. M.Jaradat, F.Awawdeh, O. Alsayyed // Analele Universitatii, Oradea Fasc. Matematica.- 2009. - V XVI. - P. 247-257.
- Rashidinia J. Taylor series method for the system of linear Volterra integro-differential equations / J.Rashidinia, A. Tahmasebi // Journal of Mathematics and Computer Science. - 2012. - Vol. 4, No. 3.- P. 331-343.
- Muratalieva V.T. Method and algorithm to investigate integro-differential equations with analytical functions / V.T. Muratalieva // Tezisy III Mezhdunarodnoj nauchn. konf. ”Borubaevskie chtenija” 2019. [Abstracts of III International scientific. conf. “Borubaev readings”], Bishkek / Institut Matematiki Nacional'noj akademii nauk Kyrgyzskoj Respubliki [Institute of Mathematics of the National Academy of Sciences of the Kyrgyz Republic].- Bishkek, 2019.- p. 48.
- Muratalieva V.T. Algoritm dlja issledovanija spektral'nyh svojstv linejnyh zadach s analiticheskimi [Algorithm for studying the spectral properties of linear problems with analytic functions] / V.T. Muratalieva // Vestnik zhalal-abadskogo gosudarstvennogo universiteta [Bulletin of Jalal-Abad State University]. – 2016.-№ 1(32). - P. 55–59.[in Russian]
